Принцип Дирихле 2011 l Кролики Древнего

Принцип Дирихле 2011

l Кролики – Древнего Китая l Кролики – Фибоначчи l Кролики - Дирихле

Формулировка принципа Дирихле Если множество из N элементов разбито на n непересекающихся частей, не имеющих общих звеньев, где N > n, то по крайней мере, в одной части будет более одного элемента. l При любом отображении множества P, содержащего n+1 элементов, в множество Q, содержащее n элементов, найдутся два элемента множества P, имеющих один и тот же образ. l Если в n “клетках” сидят не менее n+1 “кроликов”, то найдется “клетка”, в которой сидит, по крайней мере, не менее двух “кроликов”. l

В ковре размером 3 х3 метра моль проела 8 дырок. Докажите, что из него можно вырезать коврик размером 1 х1 метр, не содержащий внутри себя дырок. Так ковриков «клеток» 9 штук , а дырок - «кроликов» 8 , то найдется хотя бы одна пустая «клетка» , то есть найдется коврик без дырок внутри.

Что есть «клетки» , а что есть «кролики» ?

Петер Густав Лежен Дирихле (1805 – 1859 г. г. ) l Теорема Ферма xn+yn=zn

Обобщение принципа Дирихле 1. 2. 3. 4. Если в n клетках сидят не более n-1 кроликов, то есть пустая клетка. Если в n клетках сидят ровно n кроликов, то либо в каждой клетке ровно один кролик, либо есть и пустая клетка, и клетка, в которой не менее двух кроликов. Если в n клетках размещены не менее nk+1 кроликов, то найдутся не менее k+1 кроликов, которые посажены в одну клетку. Если в n клетках размещены не более nk-1 кроликов, то в какой то из клеток сидит не более k-1 кроликов.

На олимпиаде 10 школьников решили в сумме 35 задач, причем среди них были решившие ровно 1 задачу, ровно 2 задачи и ровно три. Доказать, что кто-то из них решил не менее пяти задач. Трое в сумме решили 6 задач. Остается еще 7 школьников, решивших в сумме 29 задач. Если взять задачи в качестве «кроликов» , то получится 7 · 4 + 1, т. е. k = 4, а n = 7.

Если среднее арифметическое нескольких чисел больше а, то хотя бы одно из этих чисел больше а. 5 программистов получили на всех зарплату 1750$. Каждый из них хотел купить компьютер ценой 360$

Принцип Дирихле - косвенное доказательство Допустим в лесу есть 500 000 елок, на каждой елке не более 300 000 иголок. Не обходимо показать, что как минимум у двух ёлок число иголок одинаково.

Прямая l делит плоскость на полуплоскости α и β. На этой прямой есть треугольник, но прямая не пересекает ни одну из его вершин. Может ли прямая l пересечь все его стороны?

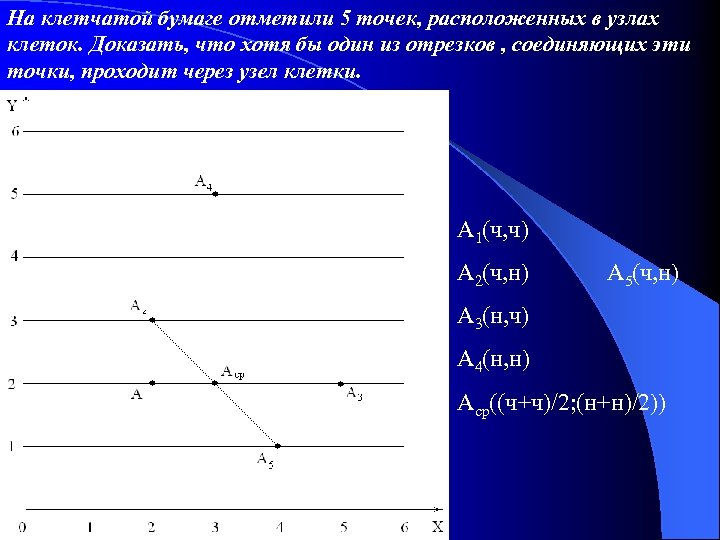На клетчатой бумаге отметили 5 точек, расположенных в узлах клеток. Доказать, что хотя бы один из отрезков , соединяющих эти точки, проходит через узел клетки. A 1(ч, ч) A 2(ч, н) А 5(ч, н) A 3(н, ч) A 4(н, н) Аср((ч+ч)/2; (н+н)/2))

Мой талисман.

Задачка на вырост. Вне шара в пространстве расположены девять точек. Докажите, что на поверхности шара найдется такая точка, из которой будет видно не более трех точек из этих девяти (шар считается непрозрачным телом).

В конференции «Молодёжь в науке» участвует 1000 учеников. Докажите, что хотя бы у 2 из них совпадает первая и последняя буква в фамилии.

Международный математический конкурс-игра «КЕНГУРУ» .