Примеры задач линейного программирования 1 Задача об

Примеры задач линейного программирования

1. Задача об использовании ресурсов (задача планирования производства)

1. 1. Для изготовления двух видов продукции P 1 и P 2 используют четыре вида ресурсов S 1, S 2, S 3 и S 4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл. 1 (цифры условные).

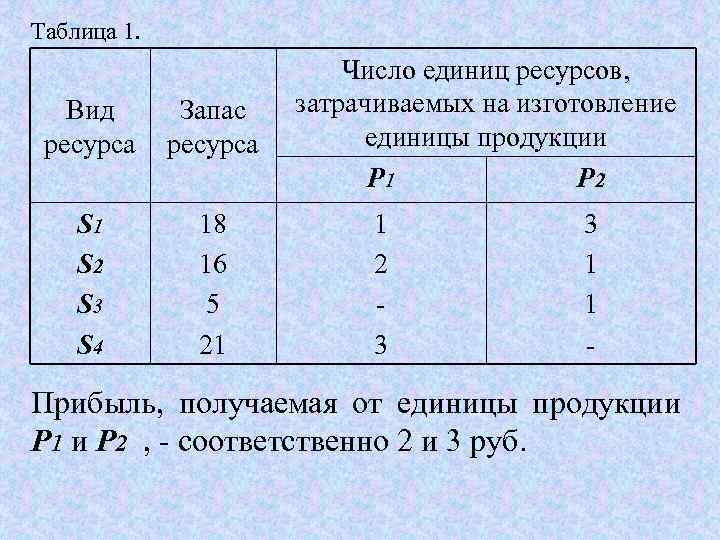
Таблица 1. Вид ресурса Запас ресурса S 1 S 2 S 3 S 4 18 16 5 21 Число единиц ресурсов, затрачиваемых на изготовление единицы продукции P 1 P 2 1 2 3 3 1 1 - Прибыль, получаемая от единицы продукции P 1 и P 2 , - соответственно 2 и 3 руб.

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Решение. Составим экономикоматематическую модель задачи.

Обозначим x 1 и x 2 — число единиц продукции соответственно P 1 и P 2, запланированных к производству. Для их изготовления (см. табл. 1) потребуется (1 x 1+ 3 x 2) единиц ресурса S 1, (2 x 1+1 x 2) единиц ресурса S 2, (1 x 2) единиц ресурса S 3 и 3 x 1; единиц ресурса S 4.

Так как потребление ресурсов S 1, S 2, S 3 и S 4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств: (1)

По смыслу задачи переменные (2) Суммарная прибыль F составит 2 x 1 руб. от реализации продукции P 1 и 3 x 2 руб. — от реализации продукции , т. е. (3)

Итак, экономико-математическая модель задачи: найти такой план выпуска продукции Х=(x 1, x 2), удовлетворяющий системе (1) и условию (2), при котором функция (3) принимает максимальное значение. Задачу легко обобщить на случай выпуска п видов продукции с использованием т видов ресурсов.

Обозначим хj (j = 1, 2, . . . , п) — число единиц продукции Pj, запланированной к производству; bi (i =1, 2, . . . , т) — запас ресурса Si, aij – число единиц ресурса Si , затрачиваемого на изготовление единицы продукции Pj (числа aij часто называют технологическими коэффициентами); cj— прибыль от реализации единицы продукции Pj.

Тогда экономикоматематическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план Х=(x 1, x 2, …xn) выпуска продукции, удовлетворяющий системе

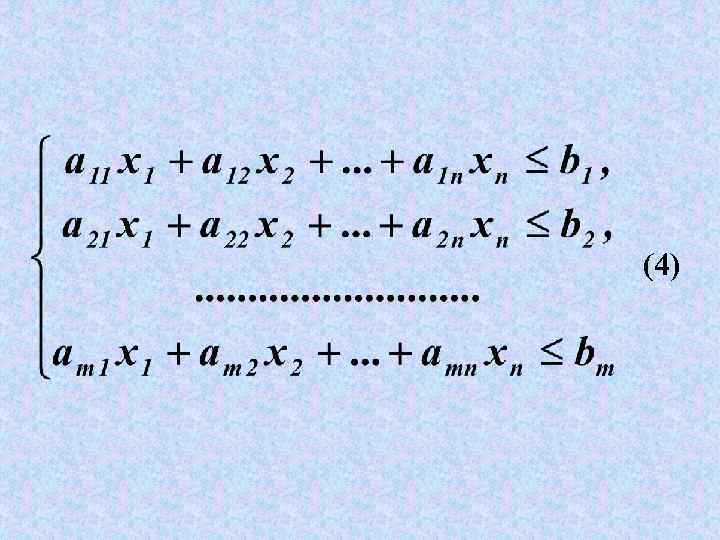
(4)

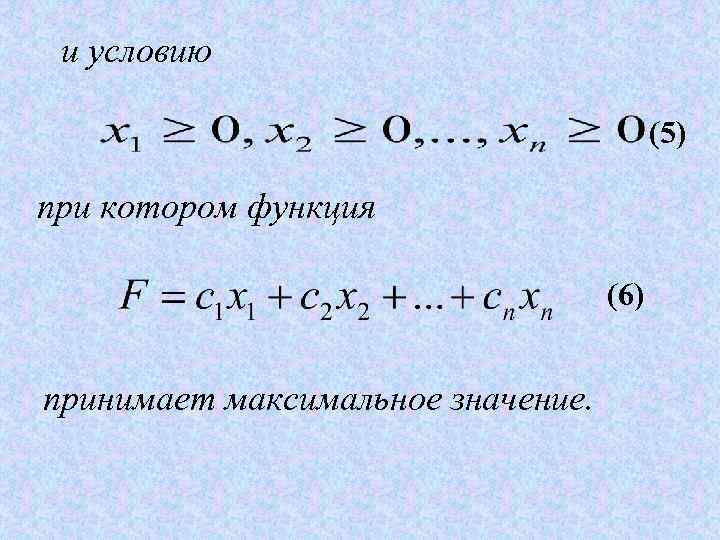
и условию (5) при котором функция (6) принимает максимальное значение.

2. Задача составления рациона (задача о диете, задача о смесях) Имеется два вида корма I и II, содержащие питательные вещества (витамины) S 1, S 2 и S 3. Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в табл. 2 (цифры условные).

Таблица 2. Вид ресурса Запас ресурса S 1 S 2 S 3 9 8 12 Число единиц питательных веществ в 1 кг корма I II 3 1 1 1 2 6

Стоимость 1 кг корма I и II соответственно равна 4 и 6 руб. Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных, веществ было бы не менее установленного предела.

Решение. Составим экономико-математическую модель задачи. Обозначим x 1 и x 2 — количество кормов I и II, входящих в дневной рацион. Тогда этот рацион (см. табл. 2) будет включать (3 x 1+1·x 2) единиц питательного вещества S 1, (1·x 1+2·x 2) единиц вещества S 2 и (1·x 1+6·x 2) единиц питательного вещества S 3.

Так как содержание питательных веществ S 1, S 2, и S 3 в рационе должно быть не менее соответственно 9, 8 и 12 единиц, то получим систему неравенств: (7)

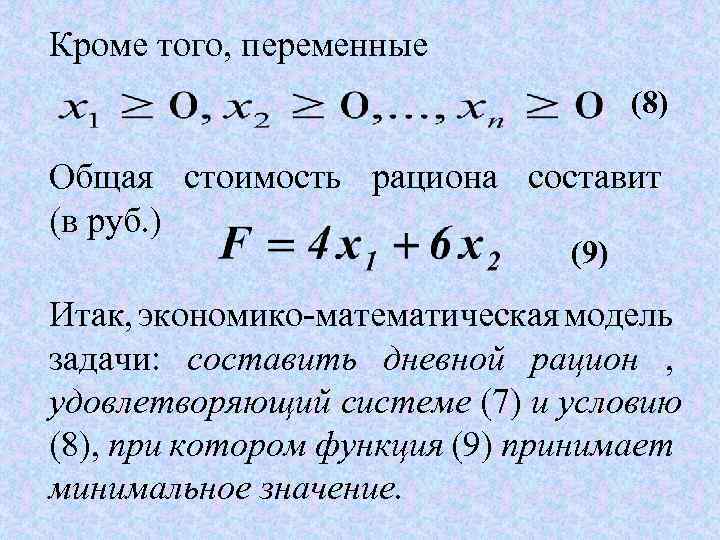
Кроме того, переменные (8) Общая стоимость рациона составит (в руб. ) (9) Итак, экономико-математическая модель задачи: составить дневной рацион , удовлетворяющий системе (7) и условию (8), при котором функция (9) принимает минимальное значение.

Для формулировки задачи в общей постановке обозначим: — число единиц корма п-го вида; — необходимый минимум содержания в рационе питательного вещества ; — число единиц питательного вещества

в единице корма j-го вида; — стоимость единицы корма j-го вида. Тогда экономико-математическая модель задачи примет вид:

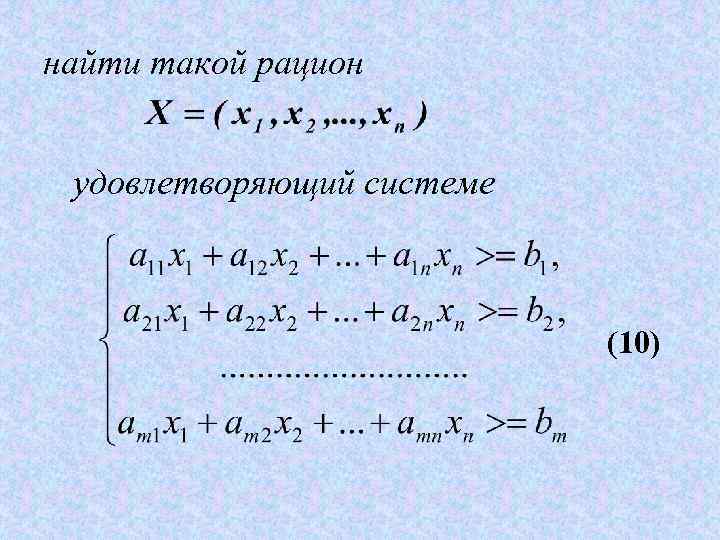
найти такой рацион удовлетворяющий системе (10)

и условию (11) при котором функция (12) принимает максимальное значение.

Геометрический метод решения задач линейного программирования

Рассмотрим задачу в стандартной форме (4)—(6) с двумя переменными (n=2). К такой форме может быть сведена и каноническая задача (с ограничениями в виде уравнений), когда число переменных п больше числа уравнений т на 2, т. е. п — т = 2.

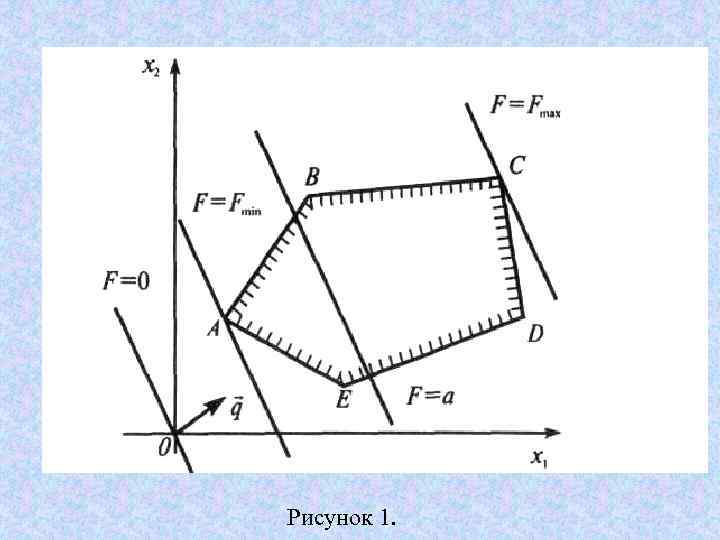
Рисунок 1.

Пусть геометрическим изображением системы ограничений является многоугольник ABCDE (рис. 1). Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F= с1 х1 + с2 х2 принимает максимальное (или минимальное) значение.

Рассмотрим так называемую линию уровня линейной функции F, т. е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение а, т. е. F = а, или (1)

Уравнение линии уровня функции (1) есть уравнение прямой линии. При различных уровнях а линии уровня параллельны, так как их угловые коэффициенты определяются только соотношением между коэффициентами с1 и с2 и, следовательно, равны. Таким образом, линии уровня функции F — это своеобразные "параллели", расположенные обычно под углом к осям координат.

Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону — только убывает.

Пусть имеются три линии уровня (I) (III) причем линия II заключена между линиями I и III. Тогда или

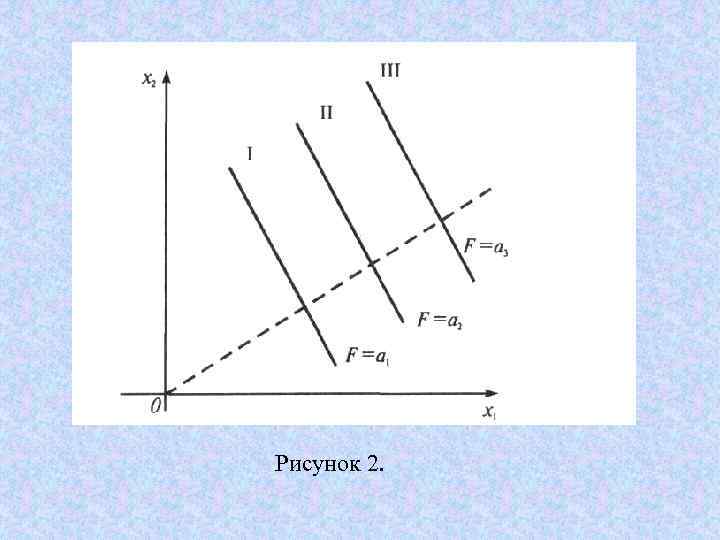
Рисунок 2.

Для определения направления возрастания рекомендуется изобразить две линии уровня и определить, на которой из них уровень больше. Например, одну из линий можно взять проходящей через начало координат (если линейная функция имеет вид т. е. без свободного члена, то это соответствует нулевому уровню).

Другую линию можно провести произвольно, так, например, чтобы она проходила через множество решений системы ограничений. Далее, определив направление возрастания линейной функции (обозначим его вектором q),

найдем точку, в которой функция принимает максимальное или минимальное значение, подобно тому как на карте находится самая северная или самая южная точка (на рис. 1 — это точка С или А).

Решить геометрически задачу 1 При ограничениях (I) (III) (IV) (V, VI)

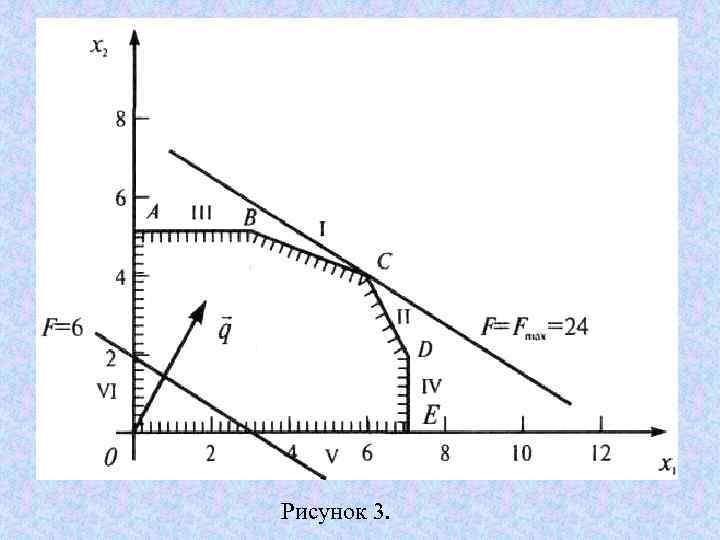
Рисунок 3.

Решение. Изобразим многоугольник решений на рис. 3. Очевидно, что при F=0 линия уровня 2 x 1+3 x 2=0 проходит через начало координат (строить ее не обязательно). Зададим, например, F=6 и построим линию уровня 2 x 1+3 x 2=6.

Ее расположение указывает на направление возрастания линейной функции (вектор q ). Так как рассматриваемая задача—на отыскание максимума, то оптимальное решение — в угловой точке С, находящейся на пересечении прямых I и II, т. е. координаты точки С определяются решением системы уравнений :

Откуда x 1=6, x 2=4, т. е. С(6; 4) Максимум (максимальное значение) линейной функции равен.

Итак, Fmax=24 при оптимальном решении x 1=6, x 2=4, т. е. максимальная прибыль в 24 руб. может быть достигнута при производстве 6 единиц продукции Р 1 и 4 единиц продукции Р 2.

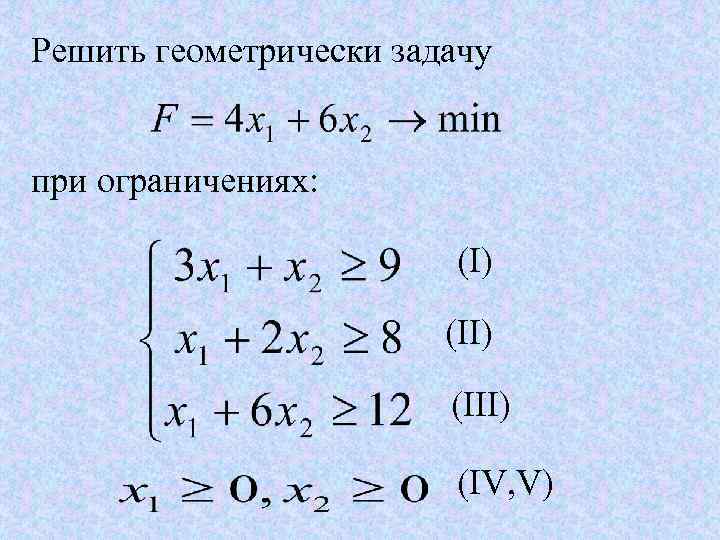
Решить геометрически задачу при ограничениях: (I) (III) (IV, V)

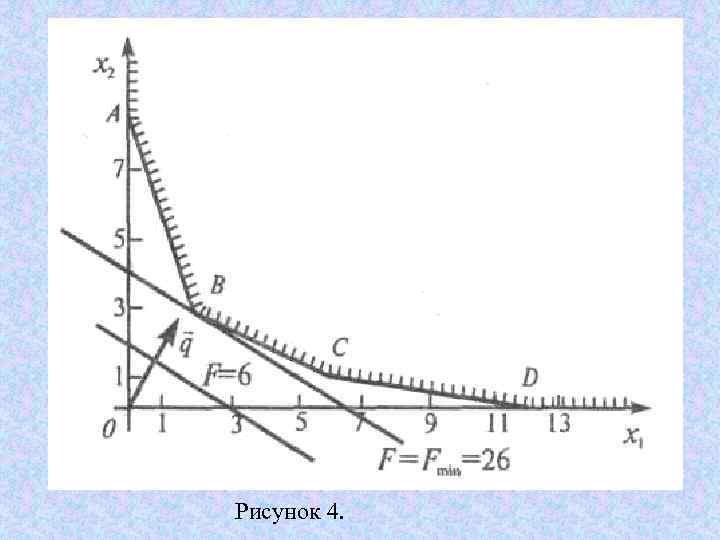
Рисунок 4.

Решение. Многоугольник решений представляет собой неограниченную многоугольную область (рис 4). По расположению линии уровня, например, F=12 или 4 х1+6 x 2=12, находим направление вектора q (этот вектор указывает на направление возрастания линейной функции).

Очевидно, что точка минимума — это точка В "входа" в многоугольник решений, ибо при дальнейшем перемещении линии уровня в направлении вектора q значения линейной функции увеличиваются. Находим координаты точки В(2; 3), при этом Fmin =4*2 +6*3 = 26.

Итак, Fmin=26 при оптимальном решении х1=2, x 2= 3, т. е. минимальная стоимость рациона 26 руб. , если в него включить 2 единицы корма I и 3 единицы корма II.

В рассмотренных задачах максимум и минимум линейной функции достигался в одной точке, так что задачи имели единственное оптимальное решение. На практике нередко встречаются задачи, которые этим условиям не удовлетворяют. В подобных случаях геометрический метод также позволяет получить ответ.

Решить геометрически следующие задачи: а) при ограничениях: (I) (III) (IV, V)

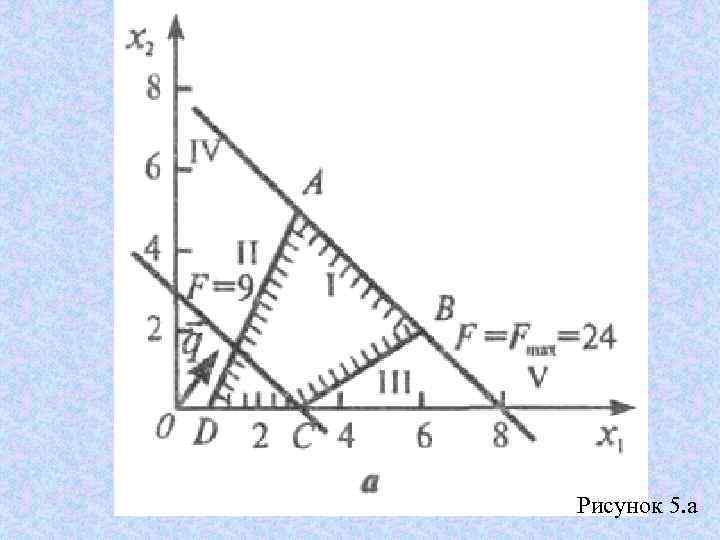
Рисунок 5. а

Решение : а) Геометрическое решение задачи показано на рис. 5, а, из которого следует, что линия уровня с максимальным уровнем совпадает с граничной линией АВ многоугольника решений ABCD, т. е. с линией х1 + х2 = 8. Следовательно, на всем отрезке АВ линейная функция F=3 x 1+3 х2 принимает одно и то же максимальное значение, равное 3(x 1+х2)=3 • 8 = 24.

Это означает, что задача имеет бесконечно много оптимальных решений (их задают координаты точек отрезка АВ), среди которых базисных оптимальных решений два — соответственно в угловых точках A(3; 5) и B(6; 2). Точки отрезка АВ задаются уравнением x 2=8 –x 1, где 3 x 1 6. Итак, Fmin= 24 при бесконечном множестве оптимальных решений х1=с, x 2=8 -c, где 3 с 6.

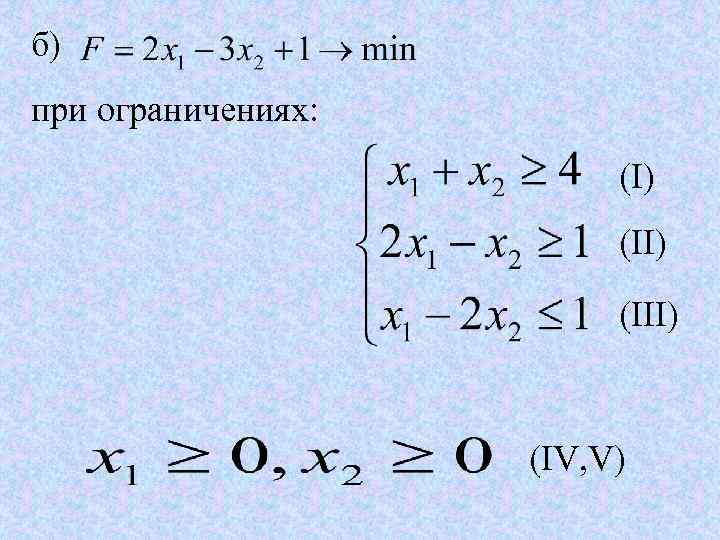
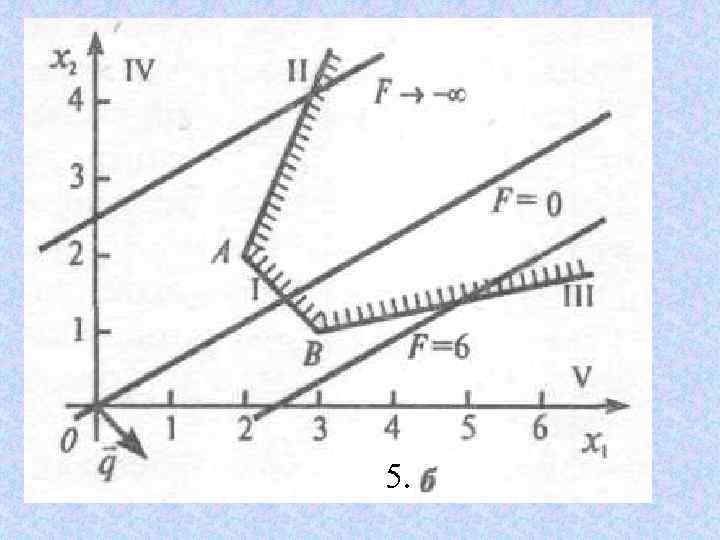
б) при ограничениях: (I) (III) (IV, V)

Замечание. При геометрическом решении подобных задач важно точно установить, действительно ли совпадает линия уровня с границей многоугольника решений или это связано с неточностью построений, мелким масштабом рисунка и т. п. Ответ на этот вопрос будет положительным, если линия уровня и граничная прямая параллельны, т. е. их коэффициенты при переменных пропорциональны. В рассматриваемом примере коэффициенты при переменных линии уровня F=3 х1+3 x 2 пропорциональны соответствующим коэффициентам граничной прямой x 1+x 2=6.

Решение : б) Геометрическое решение задачи показано на рис. 4. 5, б, из которого следует, что если линию уровня перемещать в направлении убывания линейной функции (т. е. в направлении, противоположном вектору q), то она всегда будет пересекать многоугольник решений, следовательно, линейная функция неограниченно убывает.

5.

Итак, конечного оптимума функции нет, т. е. Fmin=- линейной При геометрическом решении задач линейного программирования возможны случаи, когда условия задач противоречивы, т. е. область допустимых решений системы ограничений представляет пустое множество. Очевидно, в таких задачах нет оптимальных решений и нет смысла строить линию уровня.