Примеры картографических проекций ПРИМЕРЫ КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЙ Планарная

Примеры картографических проекций

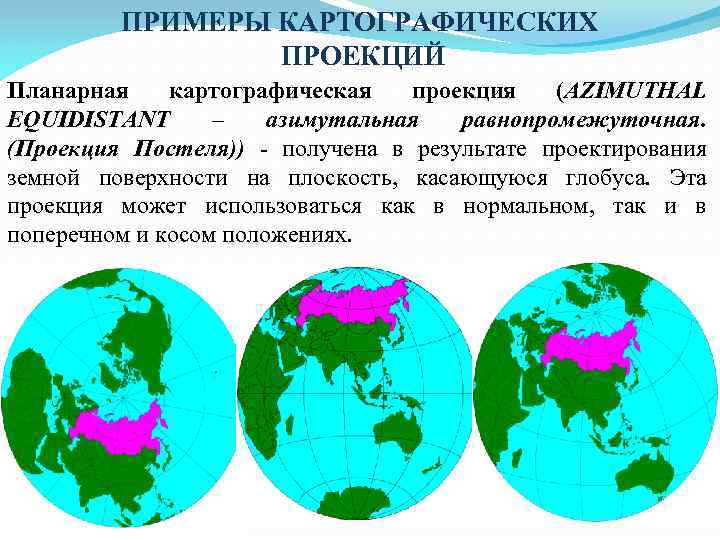ПРИМЕРЫ КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЙ Планарная картографическая проекция (AZIMUTHAL EQUIDISTANT – азимутальная равнопромежуточная. (Проекция Постеля)) - получена в результате проектирования земной поверхности на плоскость, касающуюся глобуса. Эта проекция может использоваться как в нормальном, так и в поперечном и косом положениях.

Искажения: Любая часть земного шара, ограниченная окружностью, изображается с меньшим относительным искажением длин, чем в какой бы то ни было другой проекции. Проекция AZIMUTHAL EQUIDISTANT широко применяется для территорий, имеющих округлую форму. В случае, если территория имеет малые размеры, то в этой проекции можно создавать карты крупного и среднего масштаба. Применяется в тех случаях, когда желают в какой-нибудь точке карты сохранить без искажений азимуты и расстояния от этой точки, до любой другой (авиационные, сейсмические карты с аэропортом или сейсмической станцией в центре).

LAMBERT CONFORMAL CONIC – коническая равноугольная Ламберта Искажения: Данная проекция является равноугольной (конформной), следовательно в ней сохраняется подобие малых форм и направление как на мелко-, так и на крупномасштабных картах. Площади имеют минимальные искажения около стандартных параллелей. Масштаб площадей уменьшается в промежутке между стандартными параллелями и увеличивается за их пределами. Использование: Проекция LAMBERT CONFORMAL CONIC используется для изображения среднеширотных регионов, желательный предел по широте 35°.

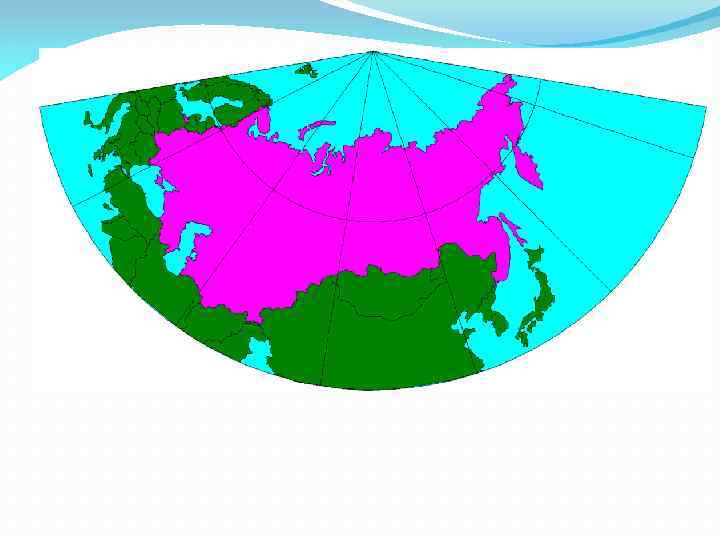
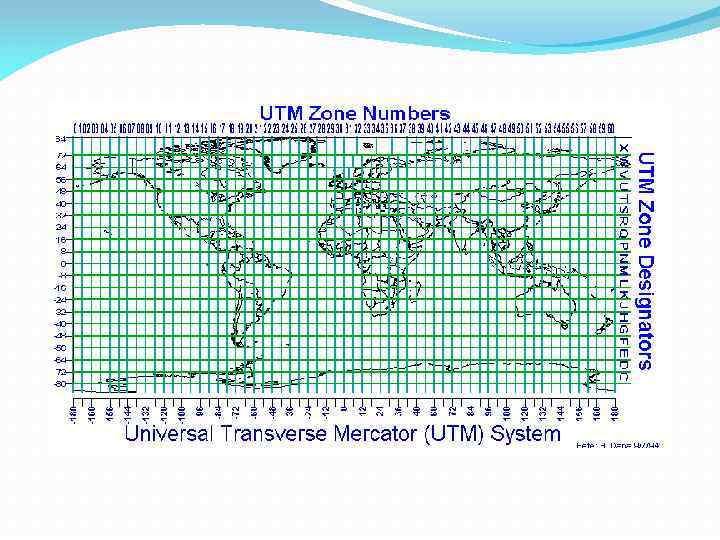
UTM (UNIVERSAL TRANSVERSE MERCATOR) – универсальная поперечно-цилиндрическая проекция Меркатора (используют для картирования больших областей. В этой проекции Земля делится на 60 шестиградусных зон (6°х 60=360°). Зоны пронумерованы от 1 до 60 начиная от 180° з. д. Каждая зона имеет свой центральный меридиан. Проекция UTM основана на цилиндре, ориентированном параллельно экватору, поэтому она является поперечной. Координаты UTM выражаются в метрах.

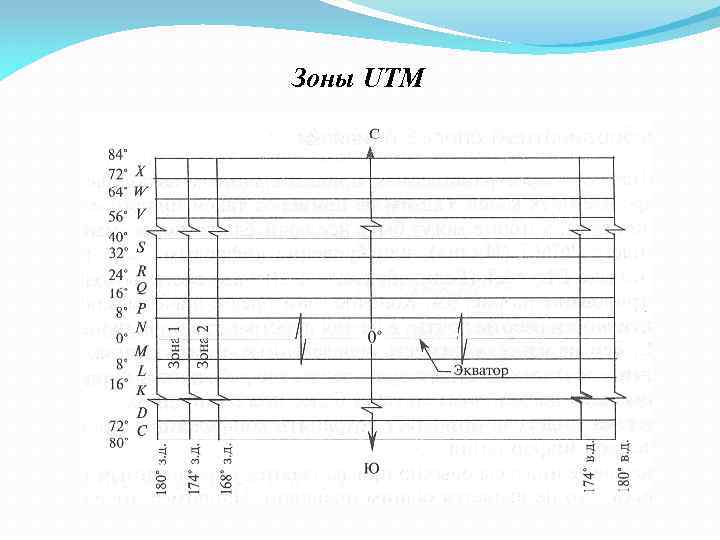Зоны UTM

Европа в проекции Меркатора

Отcчёт по оси Х (направление на восток) идёт от центрального меридиана зоны. Отcчёт по оси Y (направление на север) начинается от экватора. Чтобы исключить отрицательные координаты, проекция изменяет значения в начале координат. Величина сдвига от центрального меридиана это ложный восточный сдвиг, он равен 500000 метров; величина сдвига от экватора – ложный северный сдвиг (0 метров). Для того чтобы избежать искажений, которые возникают вблизи полюсов, в каждой зоне проецируется только область между 840 с. ш. и 800 ю. ш.

Искажения: Проекция UTM является конформной, т. е. сохраняет форму с точным соблюдением малых форм и минимальными искажениями крупных форм внутри зоны. В определённых пределах также сохраняется направление. Имеются небольшие искажения площади. Масштаб постоянен вдоль центрального меридиана при факторе масштаба 0. 9996, чтобы сократить широтные искажения внутри каждой зоны. Для компенсации искажений вблизи границ зоны – используют коэффициент, равный 1. 0004. Использование: Проекция UTM рассчитана на ошибку по масштабу не более 0. 1% внутри каждой зоны. Т. к. искажения увеличиваются на территории, занимающей более одной зоны, UTM не может быть лучшей проекцией во всех случаях.

Параметры (для первой зоны): Longitude of the Central Meridian: -177 (долгота центрального меридиана зоны) Latitude of the Origin of the Projection: 0 (широта точки начала отсчета координат) Scale Factor: 0. 9996 (масштабный коэффициент, т. е. степень уменьшения на центральном меридиане) (Scale Reduction Factor at the Central Meridian) False Easting: 500000 (ложный восточный сдвиг)(смещение начала отсчета координат в метрах) False Northing: 0 (ложный северный сдвиг) (смещение начала отсчета координат)

ПРОЕКЦИЯ ГАУССА-КРЮГЕРА – равноугольная поперечная цилиндрическая Проекция Гаусса была принята как основа для системы плоских прямоугольных координат, определяющих положение опорных геодезических пунктов на земной поверхности. Они применяются в пределах каждой шестиградусной зоны. Так как все 60 шестиградусных зон тождественны между собой, то, чтобы знать, в какой зоне находится точка, заданная прямоугольными координатами, необходимо указать номер зоны. Принято номер шестиградусной зоны, в которой лежит данная точка, приписывать впереди перед ординатой точки. Записанные так ординаты называются условными.

Если известен номер шестиградусной зоны, то долготу осевого меридиана от Гринвича можно определить по формуле: Отличие от проекции UTM заключается в том, что нумерация шестиградусных зон начинается от первой зоны, примыкающей к Гринвичскому меридиану с востока, следовательно номер n шестиградусной зоны проекции Гаусса-Крюгера связан с номером N зоны проекции UTM соотношением n=N-30 (рис. ). А также в том, что в ней на среднем меридиане частный масштаб длин равен 1. В нашей стране эта проекция применяется для топографических карт, начиная с масштаба 1: 500000 до самых крупных.

Использование: Проекция Гаусса-Крюгера может быть использована для построения карт масштаба 1: 500000 и крупнее с охватом территорий, простирающихся по долготе до 32° с искажениями длин, не превосходящими 4%. Параметры (для первой зоны): Longitude of the Central Meridian: 3 (долгота центрального меридиана зоны) (что соответствует 31 зоне проекции UTM) Latitude of the Origin of the Projection: 0 (широта точки начала отсчета координат) Scale Factor: 1 (масштабный коэффициент на центральном меридиане) (Scale Reduction Factor at the Central Meridian) False Easting: 500000 (ложный восточный сдвиг) False Northing: 0 (ложный северный сдвиг)

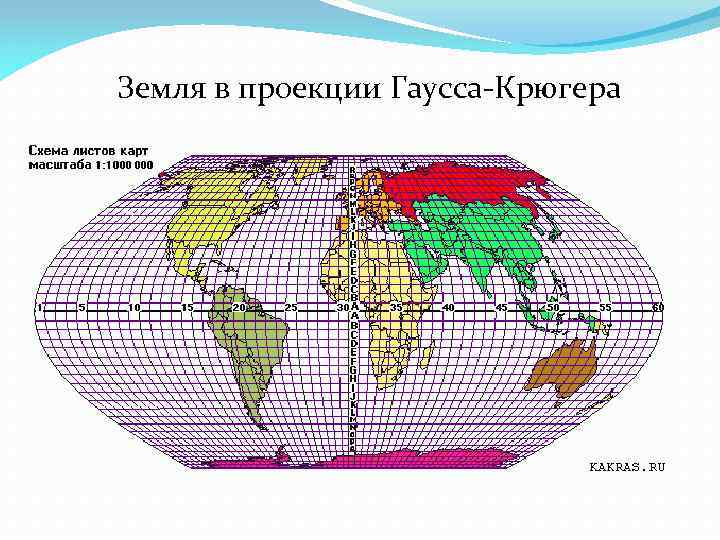Земля в проекции Гаусса-Крюгера

Согласно этой разграфке изображение поверхности земли делится параллелями на пояса (ряды), а меридианами — на колонны. Образующиеся при этом трапеции и представляют собой листы карты масштаба 1: 1 000 с размерами рамок 4° по широте и 6° по долготе. Пояса обозначаются латинскими буквами от А до U, начиная от экватора к обоим полюсам; колонны — арабскими цифрами от 1 до 60, начиная от меридиана с долготой 180° с запада на восток.

Схема разграфки листов карты масштаба 1: 1 000 для территории СССР

Номенклатура листа карты масштаба 1 : 1 000 состоит из буквы, обозначающей пояс, и номера колонны. Например: номенклатура листа с изображением г. Киев будет М— 36, г. Владивосток К— 52, г. Смоленск N – 36

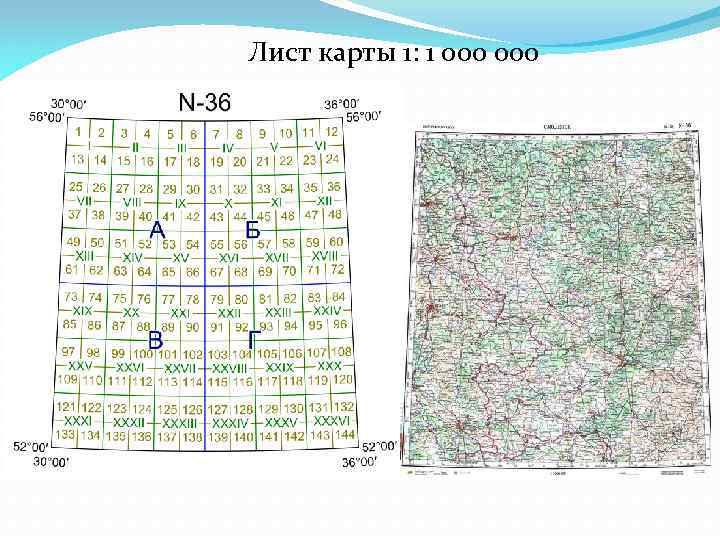Лист карты 1: 1 000

Лист карты масштаба 1: 1 000 делится на 4 листа карты масштаба 1: 500 000, которые обозначаются заглавными буквами русского алфавита: А, Б, В, Г. По широте лист карты масштаба 1: 500 000 имеет протяжение 2°, а по долготе 3°. Номенклатура листа карты масштаба 1: 500 000 включает номенклатуру миллионного листа с добавлением соответствующей буквы, например: М — 36—Г.

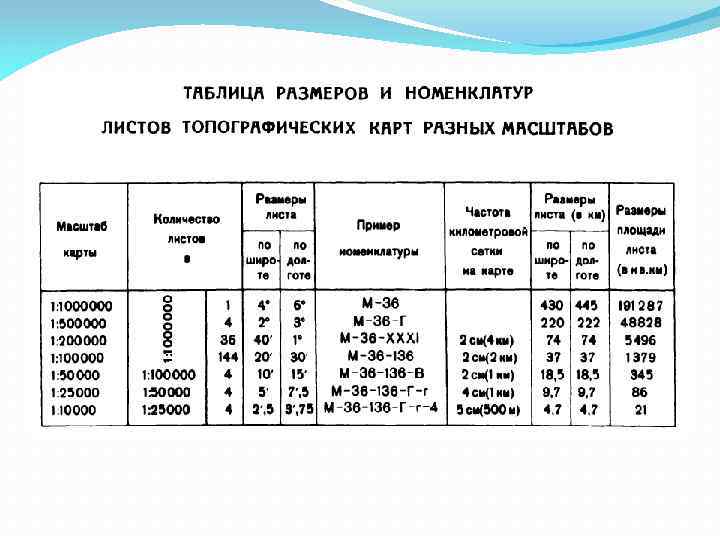
Лист карты масштаба 1 : 100 000

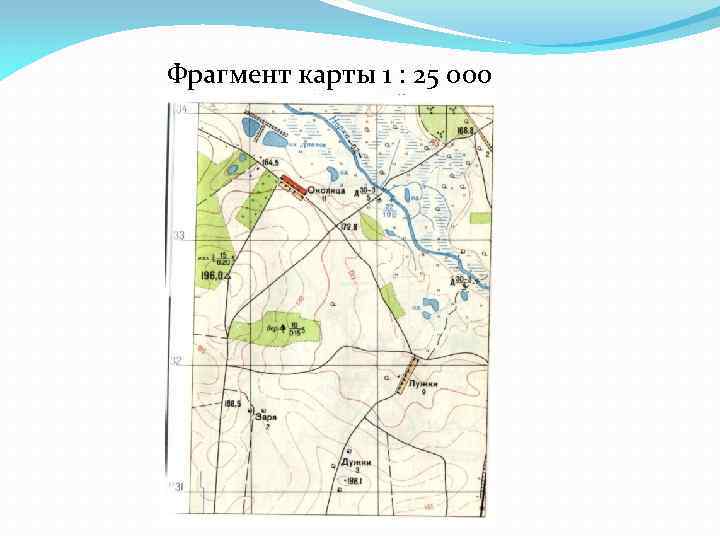Фрагмент карты 1 : 25 000

Пространственные модели

Пространственные модели Способ представления данных в ГИС – цифровая модель. Модели данных связывают физическое описание объектов с их цифровым представлением. Процесс создания модели: 1. Идентификация пространственных объектов в рамках решаемой задачи и определение способах их представления концептуальной модели. 2. Выбор растрового или векторного типа представления модели. 3. Выбор пространственных данных для хранения модели на компьютере.

Пространственное модели Объекты – дискретны, а их местоположение точно определено (здания, дороги, точки опробования и др. ) Поля – распределены непрерывно по большой площади (поля концентраций, температура, население, осадки и др. ). С учетом этих различий используют модели трех типов: 1. Объективная модель – географическое пространство заполнено отдельными идентифицируемыми объектами (четкие здания, дороги и др. )и нечеткие объекты (месторождения ПИ, ландшафтные зоны); 2. Полевая модель - географическое пространство заполнено данными которые непрерывно распределены в пространстве без четко определенных границ (поля). Возможен смешанный вариант модели – Объективная модель с обобщением по площади – обобщенная характеристика или концентрация отдельных объектов в пределах данной области.

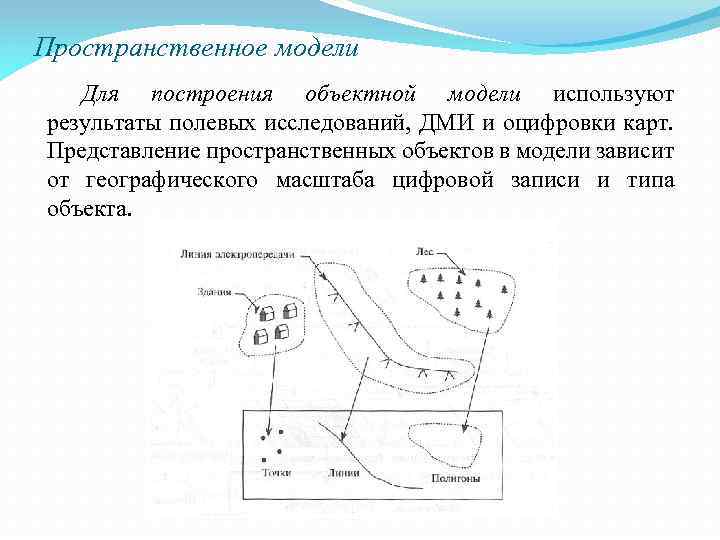Пространственное модели Для построения объектной модели используют результаты полевых исследований, ДМИ и оцифровки карт. Представление пространственных объектов в модели зависит от географического масштаба цифровой записи и типа объекта.

Пространственное модели Для получения данных полевой модели используют ДМИ, карты и полевые измерения в ряде выборочных точек, например узлов нерегулярной триангуляционной сети. Набор полевых данных можно сформировать также косвенными методами – путем интерполяции и повторной классификации. Пример: изогипсы и цифровые модели рельефа. При отображении пространственных явлений полевые данные представляют в виде поверхностей, для построения которых используют регулярную или нерегулярную мозаику.

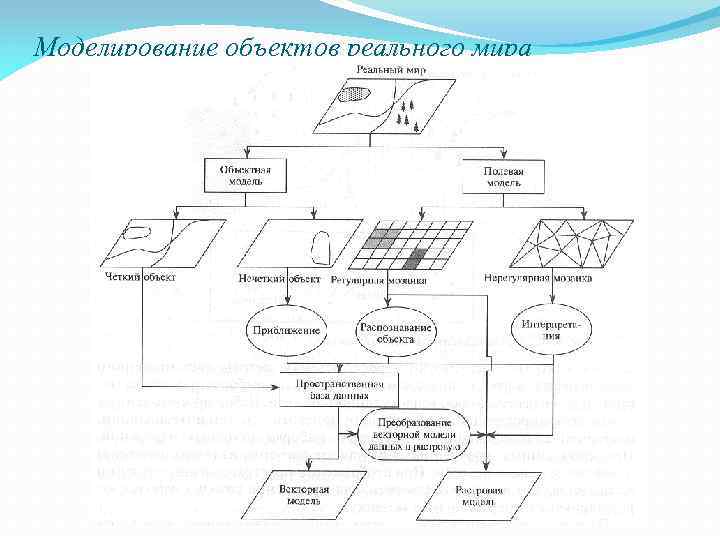Моделирование объектов реального мира

Пространственное модели При описании в ГИС пространственные объекты разделяются на множество элементарных объектовпримитивов. К ним относятся: - точки, линии, контуры, поверхности (связаны с векторным способ представления пространственных данных путем указания координат объектов и составляющих частей); - ячейки регулярных и нерегулярных пространственных сетей и пикселы - элементы разрешения изображений (связаны с растровым способом представления в виде совокупности ячеек, на которые разбиваются объекты)

Растровые модели данных Растровая модель данных – это цифровое представление пространственных объектов в виде совокупности ячеек растра (пикселов) с присвоенными им значениями классов объектов. Растровое представление предполагает позиционирование объектов указанием их положения в соответствующей растру прямоугольной матрице единообразно для всех типов пространственных объектов. Наиболее простой способ кодирования растрового изображения состоит в том, что в файл записываются числовые значения ячеек растра. Первая строка растрового файла – это заголовок с информацией о размере растра и максимальном значении ячейки.

Структуры растровых данных

Характеристики растровых моделей данных Разрешение – минимальный линейный размер наименьшего участка пространства (поверхности), отображаемый одним пикселом. Более высоким разрешением обладает растр с меньшим размером ячеек. Ориентация – угол между направлением на север и положением колонок растра. Положение – упорядоченная пара координат (номер строки и номер столбца), которые однозначно определяют положение элементов отображаемого пространства в растре. Значение – элемент информации, хранящийся в элементе растра. Зона – соседствующие друг с другом ячейки, имеющие одинаковые значения.

Достоинства растровых моделей данных - модель проста. Данные собираются по равномерной сети точек; - растровые данные проще для обработки (матричная алгебра хорошо поддается программированию); - многие растровые ГИС позволяют вводить векторные данные, тогда как обратная процедура значительно сложнее; - процессы растеризации (получения растрового изображения по векторному) много проще алгоритмически, чем процессы векторизации.

Недостатки растровых моделей данных - требуется большой объем памяти хранения данных и их обработки. компьютера для Растры часто используются при представлении и обработке аэро- и космофотоснимков и для получения данных ДМИ.

Векторные модели данных Векторная модель данных – это цифровое представление пространственных точечных, линейных и полигональных объектов в виде набора координатных пар. Нетопологическое векторное представление Простейшей структурой векторных данных является файл со списком координат (x, y) точечных объектов или точек, по которым строятся линии или полигоны.

Структуры пространственных данных Структуры векторных данных

Векторные модели данных Топологическое векторное представление данных отличается от нетопологического наличием возможности получения полного списка взаимоотношений между пространственными объектами, графическими примитивами без изменения хранимых координат для объектов. Элементы топологии, входящие в описание моделей данных ГИС, в простейшем случае определяются между элементами основных типов координатных данных.

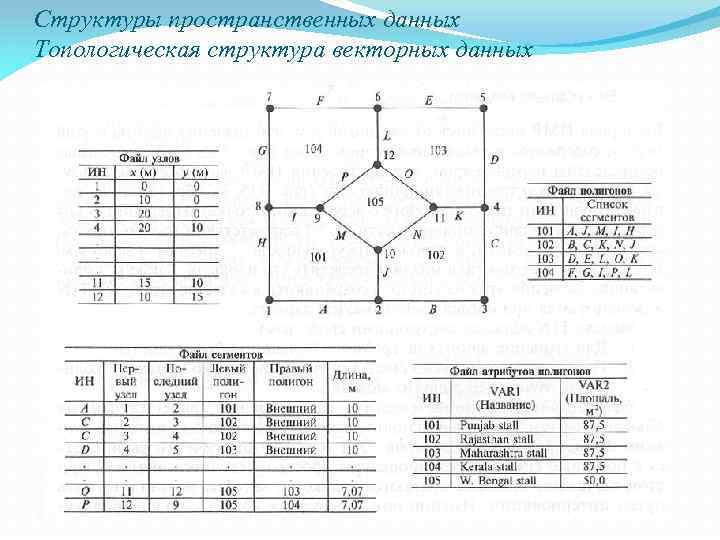Структуры пространственных данных Топологическая структура векторных данных

Векторные модели данных Фундаментальные условия для топологической структуры данных: 1. Узлы и сегменты линий не должны дублироваться. 2. Должна быть возможность включения узлов и сегментов в разные полигоны. 3. У каждого полигона должен быть уникальный идентификатор. 4. Полигоны, окруженные другими полигонами, должны воспроизводится корректно.

Векторные модели данных Топологические модели в ГИС задаются совокупностью следующих характеристик: Связанность векторов - контуры, дороги и прочие векторы должны храниться не как независимые наборы точек, а как взаимосвязанные друг с другом объекты. Связанность и примыкание районов – информация о взаимном расположении районов и об узлах пересечения их контуров вносится в базу данных.

Векторные модели данных Пересечение- информация о типах пересечений. Пример: Т-образное пересечение (трех валентное), Х-образное пересечение (четырех валентное). Близость – показатель пространственной близости линейных и полигональных объектов оценивается числовым параметром.

Структуры пространственных данных Основные топологические свойства объектов А – связанность; Б – пересечение; В - близость