Пример выполнения курсовой работы дисциплина Обработка экспериментальной информации

Пример выполнения курсовой работы (дисциплина «Обработка экспериментальной информации» )

Постановка задачи Представим себе процесс установления класса точности измерительного прибора. Для этого используется эталонный прибор, показания которого будем считать точным значением измеряемого параметра. Показания эталонного прибора записаны в файле с именем "Etalon. prn", который находится в той же папке, в которой и файл примера с именем "Варианты курсовой работы". Прочтем значение эталона в переменную etalon (поскольку запись проводится как массив, укажем нулевой элемент этого массива - он единственный) etalon: =READPRN(“Etalon. prn”) Проверим прочитанное значение (в данном примере должно быть равно 10): etalon 0=10 Процедура определения класса точности прибора состоит в проведении измерений того же параметра и определении статистических характеристик результатов (поскольку предполагается, что прибор неточный, результаты будут случайными). Представим себе, что сделано некоторое количество измерений испытываемым прибором эталонного значения и результаты записаны в файл “Data. prn”

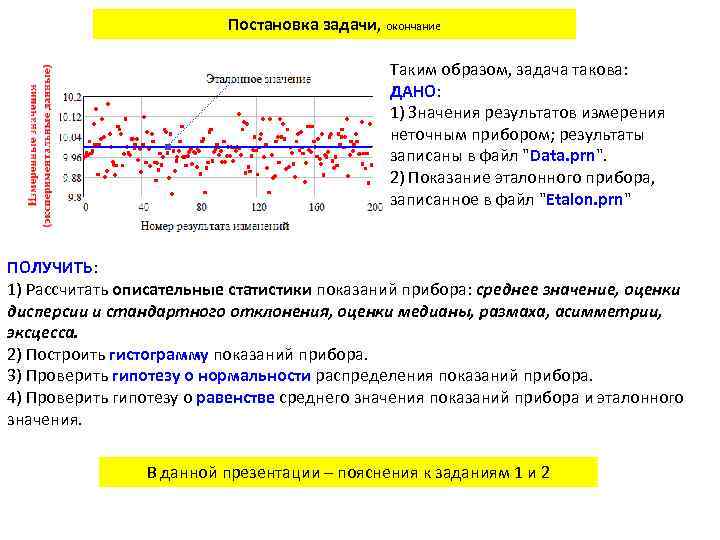
Постановка задачи, окончание Таким образом, задача такова: ДАНО: 1) Значения результатов измерения неточным прибором; результаты записаны в файл "Data. prn". 2) Показание эталонного прибора, записанное в файл "Etalon. prn" ПОЛУЧИТЬ: 1) Рассчитать описательные статистики показаний прибора: среднее значение, оценки дисперсии и стандартного отклонения, оценки медианы, размаха, асимметрии, эксцесса. 2) Построить гистограмму показаний прибора. 3) Проверить гипотезу о нормальности распределения показаний прибора. 4) Проверить гипотезу о равенстве среднего значения показаний прибора и эталонного значения. В данной презентации – пояснения к заданиям 1 и 2

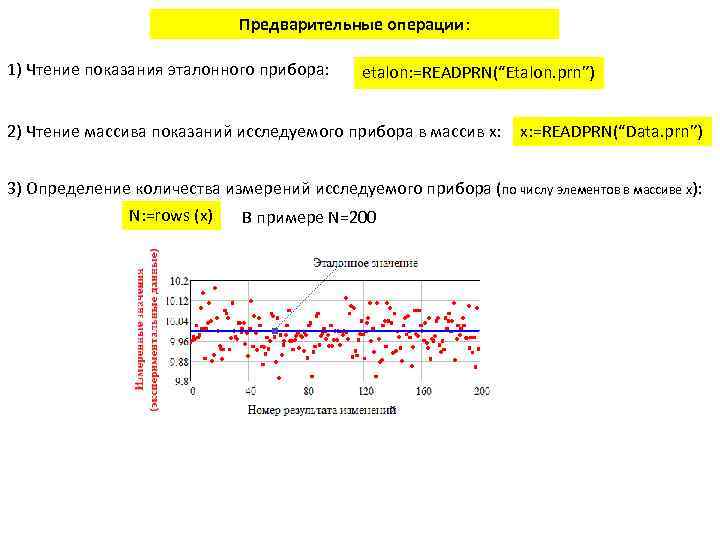
Предварительные операции: 1) Чтение показания эталонного прибора: etalon: =READPRN(“Etalon. prn”) 2) Чтение массива показаний исследуемого прибора в массив x: =READPRN(“Data. prn”) 3) Определение количества измерений исследуемого прибора (по числу элементов в массиве x): N: =rows (x) В примере N=200

Выполнение задания 1. Рассчитать описательные статистики показаний прибора: среднее значение, оценки дисперсии и стандартного отклонения, оценки медианы, размаха, асимметрии, эксцесса. Важное замечание: нужно помнить, что оценки (в отличие от статистических характеристик генеральной совокупности данных) являются СЛУЧАЙНЫМИ величинами. Точные значения статистических характеристик экспериментальных данных всегда неизвестны, и о соответствии выводов на основании рассчитанных оценок можно судть ТОЛЬКО с НЕКОТОРОЙ СТЕПЕНЬЮ УВЕРЕННОСТИ До начала расчетов ОБЯЗАТЕЛЬНО просмотрите (хотя бы бегло) поясняющие презентационные файлы "Лекция 2_описательная статистика. ppt", "Лекция 3_описат статистика_продолж. ppt" и "Лекция 4_описат статистика_оконч1. ppt". По мере выполнения этапов задания Вы можете обращаться к нужным разделам этих презентаций. Шаг 1. Определяем среднее значение (оценку математического ожидания) m. Используем соответствующую встроенную функцию Mathcad для проверки: Для проверки: вычисления с помощью встроенной Mathcadфункции должны дать то же число: Mean(x)=9. 987

Выполнение задания 1, продолжение. Шаг 2. Определяем оценку дисперсии D и стандартного отклонения σ: Шаг 3. Определяем размах Razmax как разность между максимальным xmax и минимальным xmin показаниями исследуемого прибора:

Выполнение задания 1, продолжение. Замечание: нормальное распределение относится к числу симметричных, коэффициент асимметрии теоретически равен нулю.

Выполнение задания 1, продолжение. Поскольку оценка асимметрии по ограниченному количеству данных - случайна, то она практически всегда не равна нулю, и нужны средства, позволяющие установить ее значимость. Наиболее простой способ - вычислить значение As_stand и найти отношение Asym/As_stand. Если это отношение по абсолютной величине меньше трех, асимметрию считают несущественной. В нашем примере: ((значительно меньше трех, поэтому распределение результатов измерений можно уверенно считать симметричным) Шаг 5. Определяем оценку коэффициента эксцесса, характеризующего уплощенность или островершинность графика плотности распределения результатов измерения (по сравнению с графиком для нормального распределения). Для проверки: вычисления с помощью встроенной Mathcadфункции должны дать то же число: функция вычисления эксцесса kurt(x)=-0. 073

Выполнение задания 1, продолжение. Плотности распределения вероятностей, более островершинные, чем нормальное распределение, имеют положительный коэффициент эксцесса, а более уплощенные отрицательный. Нормальное распределение имеет коэффициент эксцесса, равный нулю.

Выполнение задания 1, продолжение. Шаг 6. Определяем медиану. Для этого предварительно строим вариационный ряд результатов измерения, затем (если количество измерений - нечетное) принимаем за медиану центральный элемент массива измерений. В противном случае в качестве медианы принимаем среднее значение двух центральных элементов (в нашем случае среднее значение 99 -го и 100 го элемента массива измерений). Для определения медианы нужно составить вариационный ряд результатов измерений, т. е. упорядочить массив х по возрастанию. Медиана делит вариационный ряд пополам: половина результатов измерений меньше медианы, половина - больше.

Выполнение задания 1, продолжение. Шаг 7. Определяем моду - т. е. такое значение, при котором плотность распределения результатов измерения максимальна. Для этого нужно провести группировку данных по интервалам, в которые попадают результаты измерения. Эта же группировка понадобится при выполнении задания 2 (построение гистограммы). Мода определяется в 2 этапа. На первом находят так называемый модальный интервал - т. е. интервал, в который попало наибольшее количество результатов измерений. На втором этапе рассчитывается мода. Выполняем этап 1 шага 7. Количество интервалов группировки n_pockets (так называемые "карманы") зависит от количества данных N. Для расчета используется формула Стерджесса (в нее входит десятичный логарифм числа данных и производится округление вверх, Mathcad-функция ceil):

Выполнение задания 1, продолжение. Шаг 7. Определяем моду … (продолжение) Выполняем этап 1 шага 7. Количество интервалов группировки n_pockets (так называемые "карманы") зависит от количества данных N. Для расчета используется формула Стерджесса Для определения моды нужно определить, в какой из карманов попало наибольшее количество результатов измерения. Рассчитываем (программой) количество измерений, попавших в каждый карман, с помощью программы, определяющей количество результатов измерений, попавших в соответствующий карман.

Выполнение задания 1, продолжение. Шаг 7. Определяем моду … (продолжение) Выполняем этап 1 шага 7. Количество интервалов группировки n_pockets (так называемые "карманы") зависит от количества данных N. Для расчета используется формула Стерджесса Для определения моды нужно определить, в какой из карманов попало наибольшее количество результатов измерения. Рассчитываем (программой) количество измерений, попавших в каждый карман, с помощью программы, определяющей количество результатов измерений, попавших в соответствующий карман. Поскольку границы интервалов определены приближенно, возможно, что некоторое (небольшое) количество результатов измерения оказались не охваченными карманами. Рассчитаем это количество и увеличим размерность вектора H_pocket на 1 и присвоим его значение последнему карману:

Выполнение задания 1, окончание. Шаг 7. Определяем моду … (окончание) Выполняем этап 2 шага 7, т. е. вычисляем моду Mo. Расчетная формула: Задание 1 завершено.

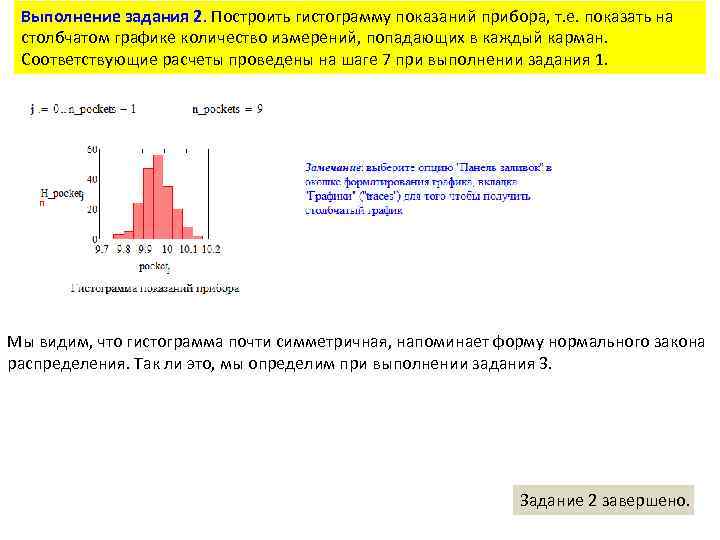
Выполнение задания 2. Построить гистограмму показаний прибора, т. е. показать на столбчатом графике количество измерений, попадающих в каждый карман. Соответствующие расчеты проведены на шаге 7 при выполнении задания 1. Мы видим, что гистограмма почти симметричная, напоминает форму нормального закона распределения. Так ли это, мы определим при выполнении задания 3. Задание 2 завершено.