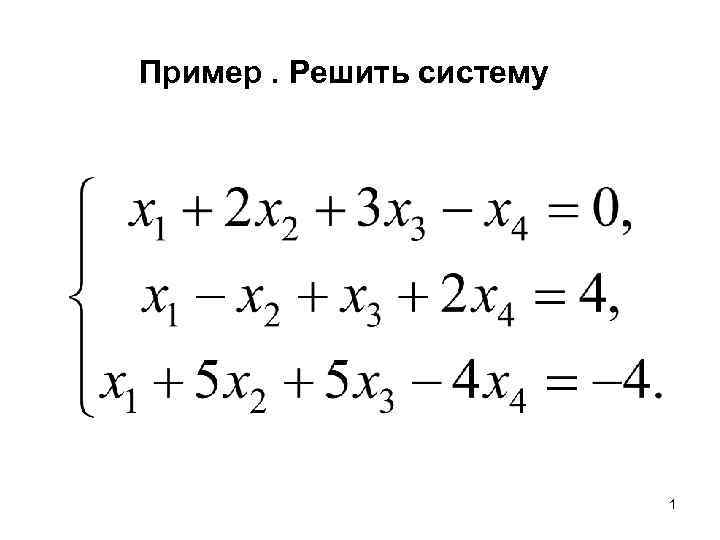 Пример. Решить систему 1
Пример. Решить систему 1
 2
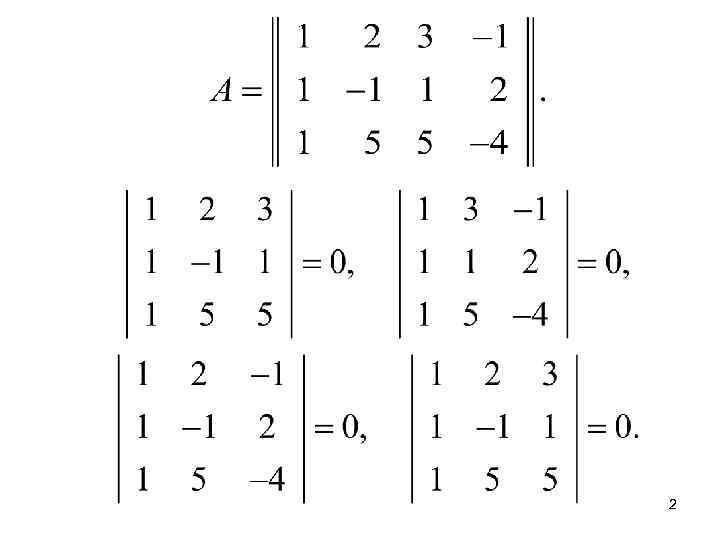
2
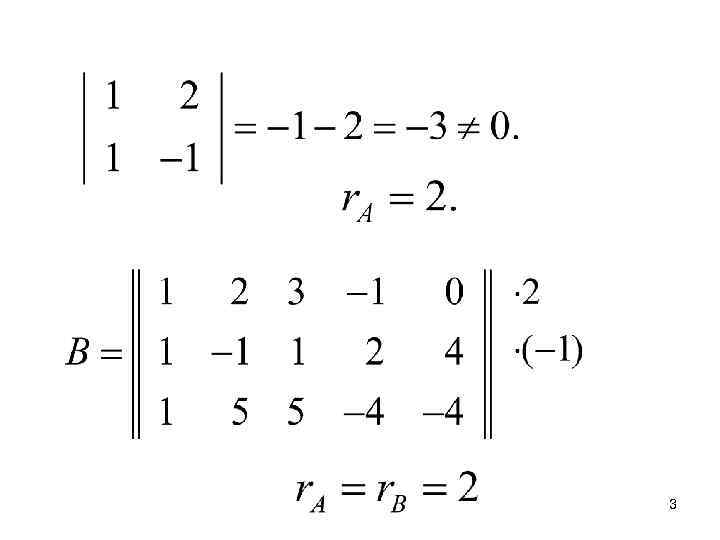 3
3
 Ранг матрицы r=2 меньше числа неизвестных n=4, поэтому система имеет бесконечное множество решений 4
Ранг матрицы r=2 меньше числа неизвестных n=4, поэтому система имеет бесконечное множество решений 4
 где и -любые числа. 5
где и -любые числа. 5
 Пример. Решить систему уравнений с помощью теоремы Крамера и с помощью обратной матрицы 6
Пример. Решить систему уравнений с помощью теоремы Крамера и с помощью обратной матрицы 6
 Решение (с помощью теоремы Крамера). 7
Решение (с помощью теоремы Крамера). 7
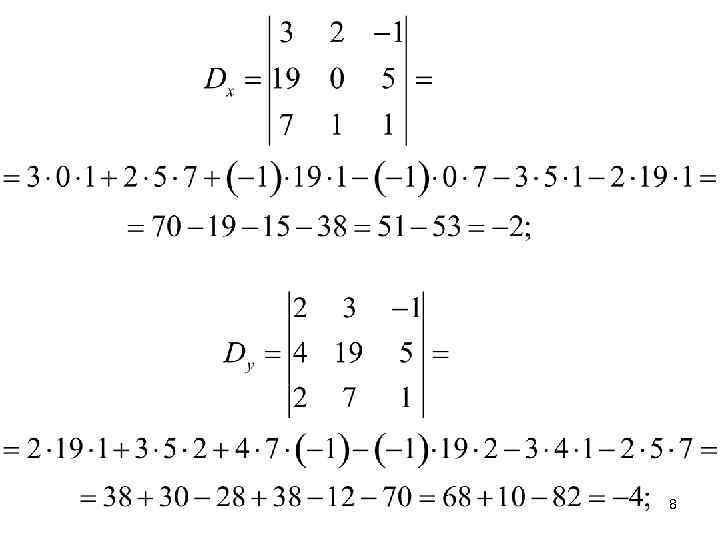 8
8
 Проверка: 9
Проверка: 9
 С помощью обратной матрицы 10
С помощью обратной матрицы 10
 11
11
 12
12
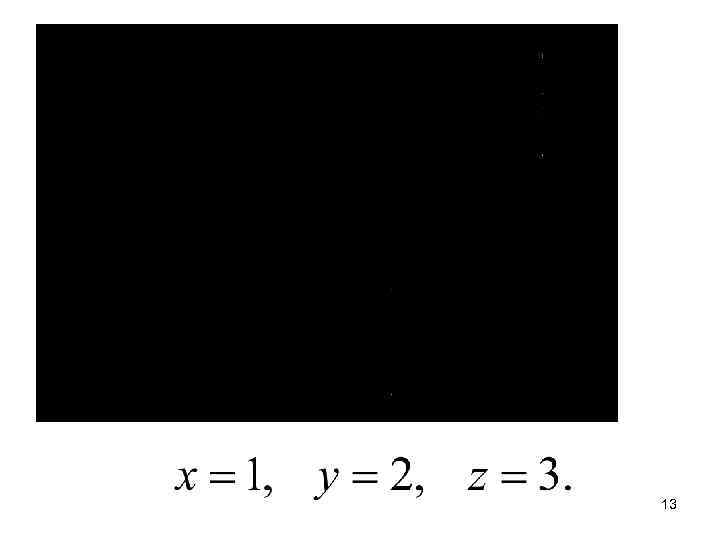 13
13
 ГЛАВА 2. Основы векторной алгебры § 1. Основные понятия и определения Вектором называется направленный отрезок, началом которого является точка A, а концом точка B. Он обозначается или B A 14
ГЛАВА 2. Основы векторной алгебры § 1. Основные понятия и определения Вектором называется направленный отрезок, началом которого является точка A, а концом точка B. Он обозначается или B A 14
 Длиной или модулем вектора называется длина отрезка AB. Она обозначается символом или. Cвободными называются векторы, которые можно переносить параллельно самим себе и откладывать от произвольной точки. Нулевым называется вектор, начало и конец которого совпадают. Нулевой вектор обозначается символом , он не имеет определенного направления, его длина равна нулю. Единичным вектором называется такой вектор, длина которого равна единице в 15 выбранном масштабе.
Длиной или модулем вектора называется длина отрезка AB. Она обозначается символом или. Cвободными называются векторы, которые можно переносить параллельно самим себе и откладывать от произвольной точки. Нулевым называется вектор, начало и конец которого совпадают. Нулевой вектор обозначается символом , он не имеет определенного направления, его длина равна нулю. Единичным вектором называется такой вектор, длина которого равна единице в 15 выбранном масштабе.
 Сонаправлеными (противоположно направлеными) называются векторы и если их направления совпадают (противоположны). Вектор, противоположный вектору обозначают (). Ортом вектора называется вектор единичной длины, сонаправленный с вектором. 16
Сонаправлеными (противоположно направлеными) называются векторы и если их направления совпадают (противоположны). Вектор, противоположный вектору обозначают (). Ортом вектора называется вектор единичной длины, сонаправленный с вектором. 16
 Коллинеарными называются векторы параллельные одной и той же прямой. Компланарными называются векторы параллельные одной и той же плоскости. Равными называются векторы, имеющие одинаковую длину и одинаковое направление. 17
Коллинеарными называются векторы параллельные одной и той же прямой. Компланарными называются векторы параллельные одной и той же плоскости. Равными называются векторы, имеющие одинаковую длину и одинаковое направление. 17
 Углом между векторами и называется наименьший угол между лучами, на которых лежат векторы и. А О B Ортогональными называются векторы если. и 18 ,
Углом между векторами и называется наименьший угол между лучами, на которых лежат векторы и. А О B Ортогональными называются векторы если. и 18 ,
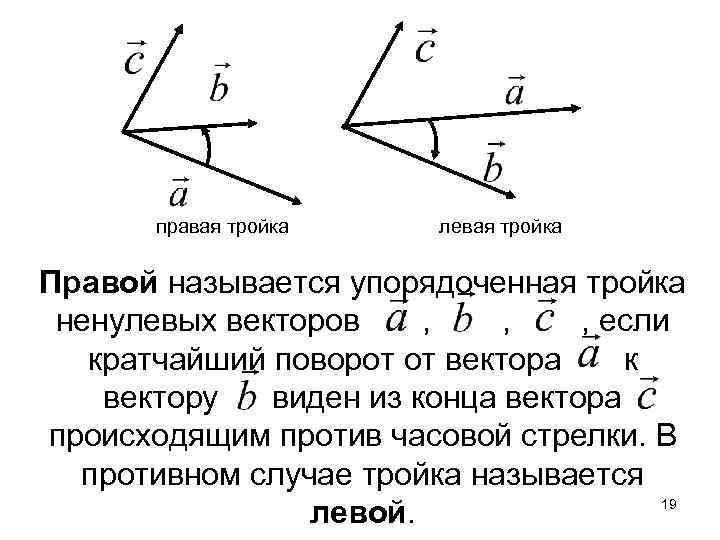 правая тройка левая тройка Правой называется упорядоченная тройка ненулевых векторов , , , если кратчайший поворот от вектора к вектору виден из конца вектора происходящим против часовой стрелки. В противном случае тройка называется 19 левой.
правая тройка левая тройка Правой называется упорядоченная тройка ненулевых векторов , , , если кратчайший поворот от вектора к вектору виден из конца вектора происходящим против часовой стрелки. В противном случае тройка называется 19 левой.
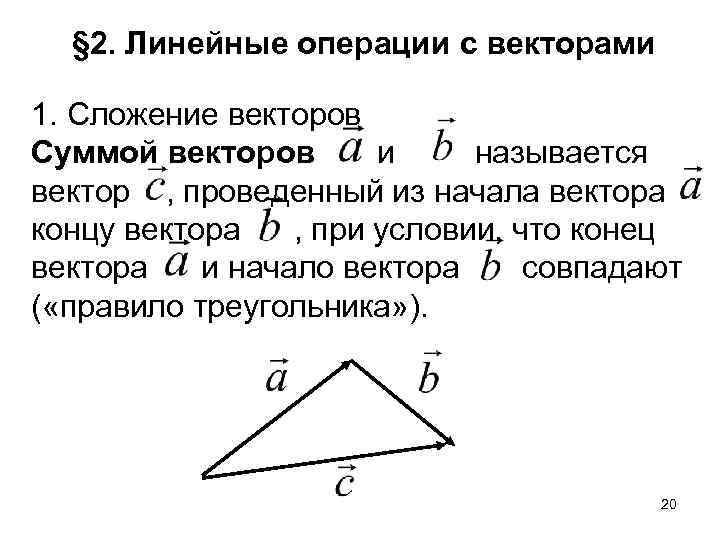 § 2. Линейные операции c векторами 1. Сложение векторов Суммой векторов и называется вектор , проведенный из начала вектора концу вектора , при условии, что конец вектора и начало вектора совпадают ( «правило треугольника» ). 20
§ 2. Линейные операции c векторами 1. Сложение векторов Суммой векторов и называется вектор , проведенный из начала вектора концу вектора , при условии, что конец вектора и начало вектора совпадают ( «правило треугольника» ). 20
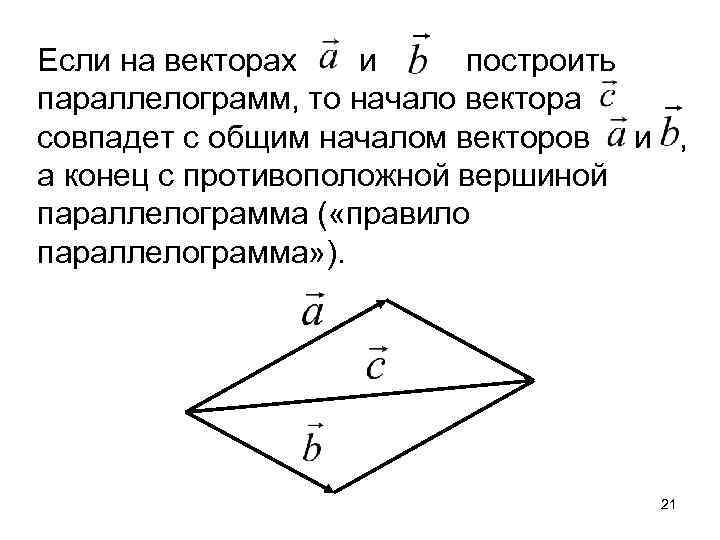 Если на векторах и построить параллелограмм, то начало вектора совпадет с общим началом векторов и , а конец с противоположной вершиной параллелограмма ( «правило параллелограмма» ). 21
Если на векторах и построить параллелограмм, то начало вектора совпадет с общим началом векторов и , а конец с противоположной вершиной параллелограмма ( «правило параллелограмма» ). 21
 Свойства операции сложения векторов: 1. ( коммутативность), 2. (ассоциативность), 3. 4. (поглощение нуля), . 22
Свойства операции сложения векторов: 1. ( коммутативность), 2. (ассоциативность), 3. 4. (поглощение нуля), . 22
 2. Вычитание векторов Разностью векторов и называется вектор равный сумме вектора и вектора , противоположного вектору. 23
2. Вычитание векторов Разностью векторов и называется вектор равный сумме вектора и вектора , противоположного вектору. 23
 3. Умножение вектора на число. Произведением ненулевого вектора на число называется вектор, длина которого равна при этом сонаправленный с , если и противоположно направленный, если Если или , то произведение считается нулевым вектором. Произведение вектора на число обозначается. 24
3. Умножение вектора на число. Произведением ненулевого вектора на число называется вектор, длина которого равна при этом сонаправленный с , если и противоположно направленный, если Если или , то произведение считается нулевым вектором. Произведение вектора на число обозначается. 24
 Свойства операции умножения вектора на число: 1. (дистрибутивность относительно сложения чисел), 2. (дистрибутивность относительно сложения векторов), 3. (ассоциативность относительно числового множителя), 4. (умножение на единицу). 25
Свойства операции умножения вектора на число: 1. (дистрибутивность относительно сложения чисел), 2. (дистрибутивность относительно сложения векторов), 3. (ассоциативность относительно числового множителя), 4. (умножение на единицу). 25
 Проекции вектора Осью называется прямая, на которой выбрано одно из двух возможных направлений, зафиксирована точка, называемая началом, и выбран масштаб для измерения длин. Выбранное направление на оси удобно задавать с помощью орта. 26
Проекции вектора Осью называется прямая, на которой выбрано одно из двух возможных направлений, зафиксирована точка, называемая началом, и выбран масштаб для измерения длин. Выбранное направление на оси удобно задавать с помощью орта. 26
 B A Проекцией вектора на ось называется число , где длина соответствующего отрезка. 27
B A Проекцией вектора на ось называется число , где длина соответствующего отрезка. 27
 Проекцией вектора на ненулевой вектор называется проекция на любую ось, одинаково направленную с. Она обозначается. 28
Проекцией вектора на ненулевой вектор называется проекция на любую ось, одинаково направленную с. Она обозначается. 28
 Свойства проекций: 1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью , т. е. 2. При умножении вектора на число, его проекция также умножится на это число, т. е. 3. Проекция суммы векторов равна сумме проекций, т. е. 29
Свойства проекций: 1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью , т. е. 2. При умножении вектора на число, его проекция также умножится на это число, т. е. 3. Проекция суммы векторов равна сумме проекций, т. е. 29
 § 3. Линейная зависимость и линейная независимость векторов Линейной комбинацией системы векторов называется сумма произведений этих элементов на произвольные числа Числа называются коэффициентами линейной комбинации. 30
§ 3. Линейная зависимость и линейная независимость векторов Линейной комбинацией системы векторов называется сумма произведений этих элементов на произвольные числа Числа называются коэффициентами линейной комбинации. 30
 Линейно зависимой называется такая система векторов , в которой из равенства нулю их линейной комбинации следует существование хотя бы одного ненулевого коэффициента данной комбинации. Линейно независимой называется система векторов, в которой указанное равенство возможно только в единственном случае, когда 31.
Линейно зависимой называется такая система векторов , в которой из равенства нулю их линейной комбинации следует существование хотя бы одного ненулевого коэффициента данной комбинации. Линейно независимой называется система векторов, в которой указанное равенство возможно только в единственном случае, когда 31.
 Теорема (Необходимое и достаточное условие линейной зависимости системы векторов). Система векторов линейно зависима, тогда и только тогда, когда хотя бы один из них может быть представлен в виде линейной комбинации остальных. Доказательство: 1)Необходимость. 32
Теорема (Необходимое и достаточное условие линейной зависимости системы векторов). Система векторов линейно зависима, тогда и только тогда, когда хотя бы один из них может быть представлен в виде линейной комбинации остальных. Доказательство: 1)Необходимость. 32
 2) Достаточность. Следствия : 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны. 3. Четыре и более вектора всегда линейно зависимы. 33
2) Достаточность. Следствия : 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны. 3. Четыре и более вектора всегда линейно зависимы. 33
 Базисом на плоскости называется упорядоченная пара неколлинеарных векторов , отложенных от одной точки. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов отложенных от одной точки. 34
Базисом на плоскости называется упорядоченная пара неколлинеарных векторов , отложенных от одной точки. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов отложенных от одной точки. 34
 Теорема. Если на плоскости выбран некоторый базис , то каждый вектор этой плоскости может быть однозначно представлен в виде: N O A M 35
Теорема. Если на плоскости выбран некоторый базис , то каждый вектор этой плоскости может быть однозначно представлен в виде: N O A M 35
 Пусть При Это означает, что и получим противоречие и 36
Пусть При Это означает, что и получим противоречие и 36
 Разложением вектора по базису векторов называется запись вектора в виде Координатами вектора в данном базисе называются коэффициенты x, y в этом разложении. Ортонормированным называется базис, все образующие векторы которого взаимно перпендикулярны и имеют единичную длину. 37
Разложением вектора по базису векторов называется запись вектора в виде Координатами вектора в данном базисе называются коэффициенты x, y в этом разложении. Ортонормированным называется базис, все образующие векторы которого взаимно перпендикулярны и имеют единичную длину. 37
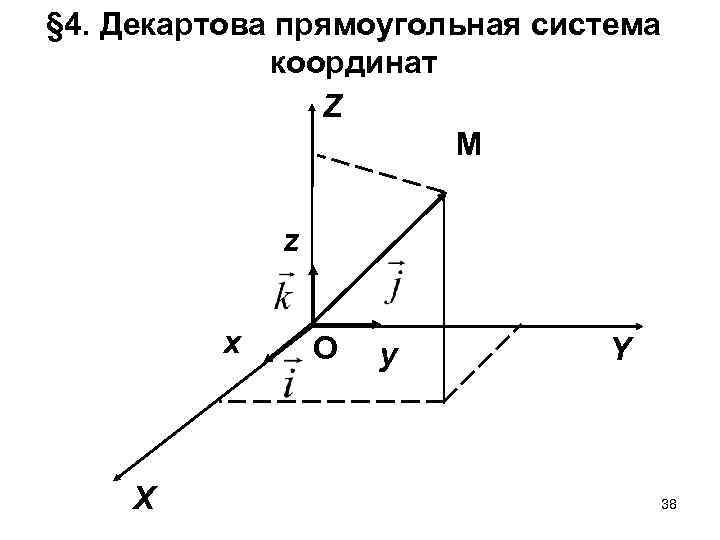 § 4. Декартова прямоугольная система координат Z M z x X O y Y 38
§ 4. Декартова прямоугольная система координат Z M z x X O y Y 38
 Декартовыми прямоугольными координатами вектора относительно данной системы координат OXYZ назовем упорядоченную тройку чисел , , . Декартовыми прямоугольными координатами точки М относительно данной системы координат OXYZ называются координаты её радиус-вектора , так что 39
Декартовыми прямоугольными координатами вектора относительно данной системы координат OXYZ назовем упорядоченную тройку чисел , , . Декартовыми прямоугольными координатами точки М относительно данной системы координат OXYZ называются координаты её радиус-вектора , так что 39
 Линейные операции над векторами в координатной форме Теорема (Координатный признак равенства векторов). Пусть , а. В фиксированной системе координат векторы равны тогда и только тогда, когда равны их координаты, т. е. 40
Линейные операции над векторами в координатной форме Теорема (Координатный признак равенства векторов). Пусть , а. В фиксированной системе координат векторы равны тогда и только тогда, когда равны их координаты, т. е. 40
 Теорема (О линейных операциях над векторами в координатной форме). 1. Координаты суммы векторов равны сумме соответствующих координат слагаемых, т. е. 2. Координаты произведения вектора на число k равны произведению соответствующих координат на это число, т. е. 41
Теорема (О линейных операциях над векторами в координатной форме). 1. Координаты суммы векторов равны сумме соответствующих координат слагаемых, т. е. 2. Координаты произведения вектора на число k равны произведению соответствующих координат на это число, т. е. 41
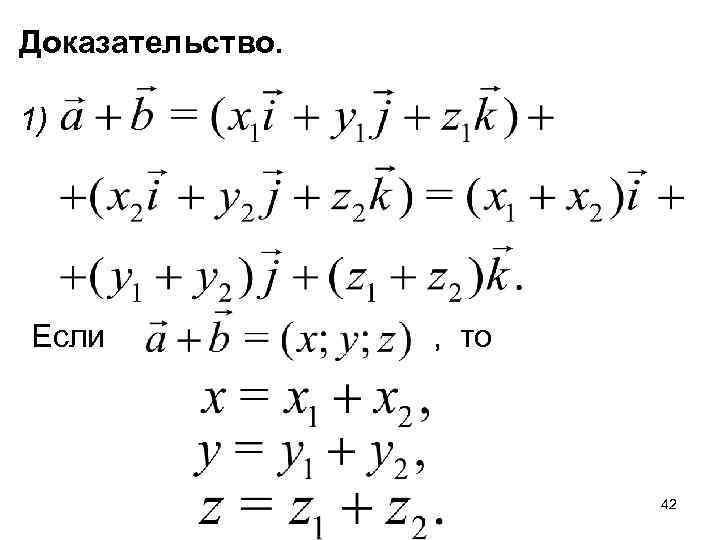 Доказательство. 1) Если , то 42
Доказательство. 1) Если , то 42
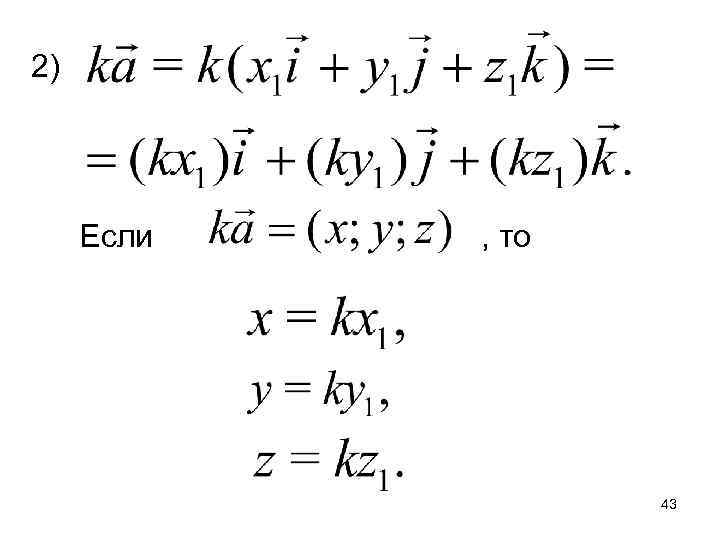 2) Если , то 43
2) Если , то 43
 Следствие 1 (Выражение координат вектора через координаты его конца и начала). Пусть координаты точек и , тогда Следствие 2 (Координатный признак коллинеарности векторов). Вектор коллинеарен вектору тогда и только тогда, когда выполнено равенство 44
Следствие 1 (Выражение координат вектора через координаты его конца и начала). Пусть координаты точек и , тогда Следствие 2 (Координатный признак коллинеарности векторов). Вектор коллинеарен вектору тогда и только тогда, когда выполнено равенство 44
 Пример. Пусть , Найти координаты вектора . . Пример. При каком значении коллинеарны векторы и. 45
Пример. Пусть , Найти координаты вектора . . Пример. При каком значении коллинеарны векторы и. 45
 § 5. Скалярное произведение векторов Скалярным произведением ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними Если =0 или = 0 то 46
§ 5. Скалярное произведение векторов Скалярным произведением ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними Если =0 или = 0 то 46
 Свойства скалярного произведения Свойство 1. (Признак ортогональности). Для того чтобы два ненулевых вектора были ортогональны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю. 47
Свойства скалярного произведения Свойство 1. (Признак ортогональности). Для того чтобы два ненулевых вектора были ортогональны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю. 47
 Доказательство. Необходимость. Если , то Достаточность. Если то и , и тогда , . Но , поэтому и 48
Доказательство. Необходимость. Если , то Достаточность. Если то и , и тогда , . Но , поэтому и 48
 Свойство 2. Угол между двумя ненулевыми векторами острый (тупой), если их скалярное произведение положительно (отрицательно). Свойство 3. Скалярное произведение двух векторов равно произведению длины одного вектора на проекцию второго на направление первого, т. е. 49
Свойство 2. Угол между двумя ненулевыми векторами острый (тупой), если их скалярное произведение положительно (отрицательно). Свойство 3. Скалярное произведение двух векторов равно произведению длины одного вектора на проекцию второго на направление первого, т. е. 49
 Свойство 4. Скалярное произведение вектора самого на себя равно квадрату длины вектора: Свойство 5. (переместительное) Свойство 6. (распределительное) Свойство 7. (сочетательное относительно скалярного множителя) 50
Свойство 4. Скалярное произведение вектора самого на себя равно квадрату длины вектора: Свойство 5. (переместительное) Свойство 6. (распределительное) Свойство 7. (сочетательное относительно скалярного множителя) 50
 Пример. Упростить выражение. . 51
Пример. Упростить выражение. . 51
 § 6. Вычисление длин векторов и углов между ними. Теорема (Выражение скалярного произведения через координаты сомножителей). Пусть даны декартовы координаты векторов и Тогда . 52
§ 6. Вычисление длин векторов и углов между ними. Теорема (Выражение скалярного произведения через координаты сомножителей). Пусть даны декартовы координаты векторов и Тогда . 52
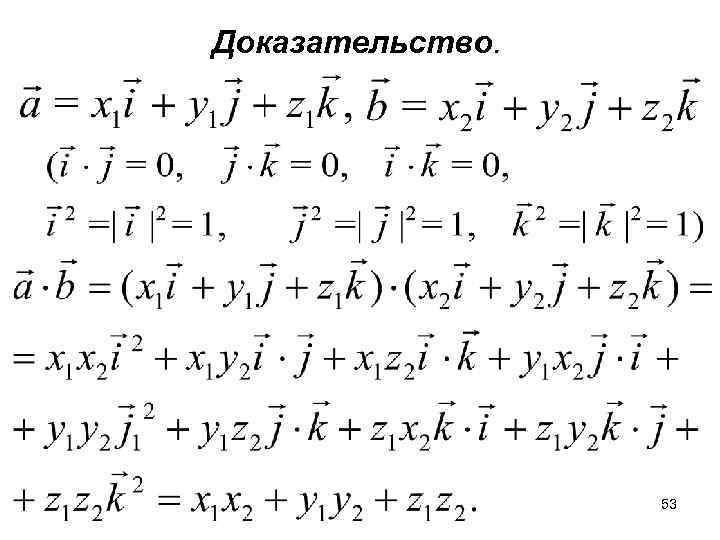 Доказательство. 53
Доказательство. 53
 Следствие 1 (Вычисление длины вектора). Если то Следствие 2 (Вычисление косинуса угла между векторами). 54
Следствие 1 (Вычисление длины вектора). Если то Следствие 2 (Вычисление косинуса угла между векторами). 54
 Следствие 3 (Координатный признак ортогональности). Следствие 4 (Вычисление проекции одного вектора на другой). 55
Следствие 3 (Координатный признак ортогональности). Следствие 4 (Вычисление проекции одного вектора на другой). 55
 Пример1. Найти угол между диагоналями параллелограмма, построенного на векторах и. Решение. 56
Пример1. Найти угол между диагоналями параллелограмма, построенного на векторах и. Решение. 56
 Пример 2. Даны координаты вершин треугольника А(1, 2, 3), В(3, 3, 0), С(4, 6, 3). Определить проекцию стороны АВ на основание треугольника АС. B A C 57
Пример 2. Даны координаты вершин треугольника А(1, 2, 3), В(3, 3, 0), С(4, 6, 3). Определить проекцию стороны АВ на основание треугольника АС. B A C 57
 Пример 3. Найти вектор длиной ортогональный векторам и , образующий тупой угол с осью OZ. 58
Пример 3. Найти вектор длиной ортогональный векторам и , образующий тупой угол с осью OZ. 58
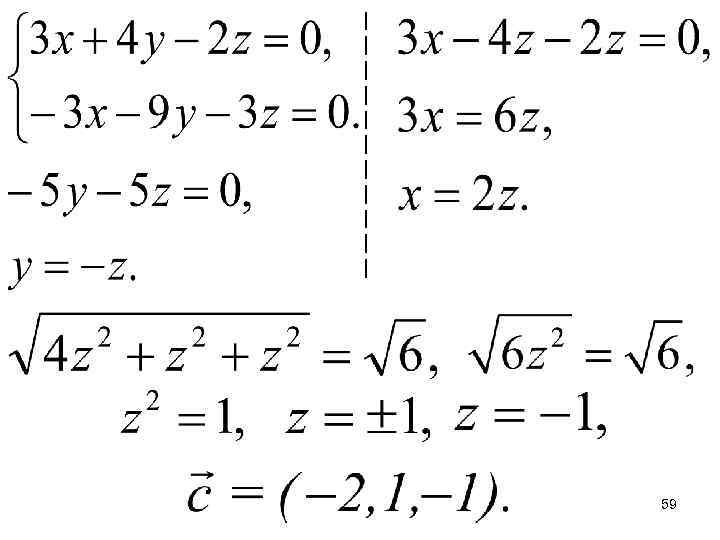 59
59
 § 7. Векторное произведение векторов Векторным произведением вектора на неколлинеарный ему вектор называется третий вектор , такой что: а) б) в) тройка векторов , , правая. 60
§ 7. Векторное произведение векторов Векторным произведением вектора на неколлинеарный ему вектор называется третий вектор , такой что: а) б) в) тройка векторов , , правая. 60
 Свойства векторного произведения: 1. (Признак коллинеарности) 2. S 3. 4. 5. 61
Свойства векторного произведения: 1. (Признак коллинеарности) 2. S 3. 4. 5. 61
 Пример. Упростить, используя свойства векторного произведения. 62
Пример. Упростить, используя свойства векторного произведения. 62
 Теорема (Вычисление векторного произведения в координатной форме). Пусть декартовы координаты векторов и , тогда Доказательство. Учтем, что 63
Теорема (Вычисление векторного произведения в координатной форме). Пусть декартовы координаты векторов и , тогда Доказательство. Учтем, что 63
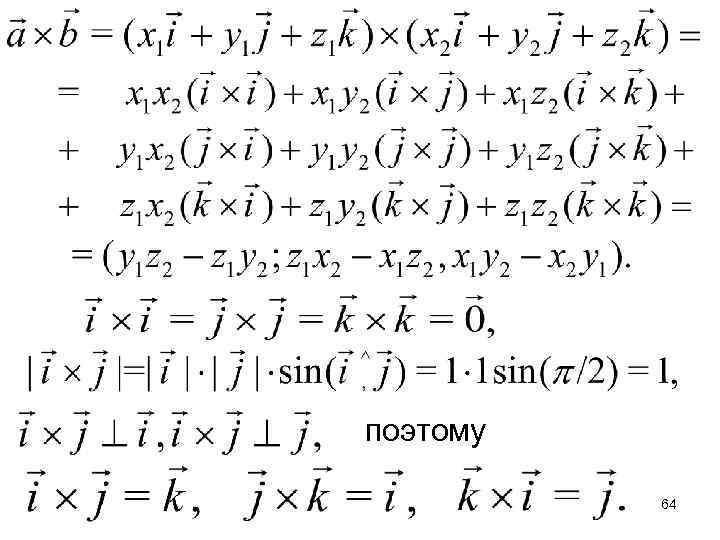 поэтому 64
поэтому 64
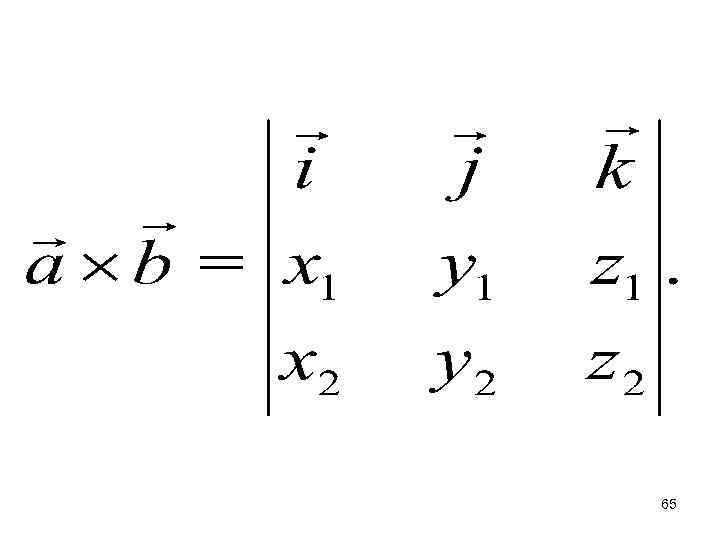 65
65
 Пример. Даны координаты вершин треугольника А(2, -1, 3), В(1, 1, 1), С(5, -2, 5). Найти площадь треугольника. Решение. B A • (ед ) C 66
Пример. Даны координаты вершин треугольника А(2, -1, 3), В(1, 1, 1), С(5, -2, 5). Найти площадь треугольника. Решение. B A • (ед ) C 66
 § 8. Смешанное произведение векторов Смешанным произведением упорядоченной тройки векторов называют число, равное скалярному произведению вектора на векторное произведение. Если хотя бы один из векторов равен нулю, то 67
§ 8. Смешанное произведение векторов Смешанным произведением упорядоченной тройки векторов называют число, равное скалярному произведению вектора на векторное произведение. Если хотя бы один из векторов равен нулю, то 67
 Свойства смешанного произведения: 1. 2. 3. 4. 68
Свойства смешанного произведения: 1. 2. 3. 4. 68
 5. (Выражение смешанного произведения через координаты сомножителей). Если известны декартовы прямоугольные координаты векторов , и , то 69
5. (Выражение смешанного произведения через координаты сомножителей). Если известны декартовы прямоугольные координаты векторов , и , то 69
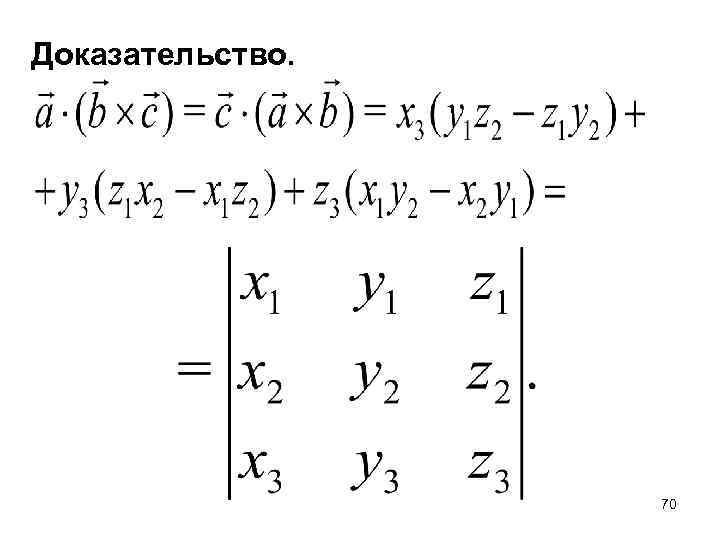 Доказательство. 70
Доказательство. 70
 6. Модуль смешанного произведения равен объему параллелепипеда, построенного на приведенных к общему началу векторах 71
6. Модуль смешанного произведения равен объему параллелепипеда, построенного на приведенных к общему началу векторах 71
 Пример 1. Доказать, что векторы , и не могут быть компланарными ни при каком значении Решение. . 72
Пример 1. Доказать, что векторы , и не могут быть компланарными ни при каком значении Решение. . 72
 Пример 2. Параллелепипед построен на векторах =(4, -3, 2), =(3, -2, 5) и =(1, 0, 3). Найти длину высоты, опущенной из конца вектора на плоскость векторов и. Решение. h 73
Пример 2. Параллелепипед построен на векторах =(4, -3, 2), =(3, -2, 5) и =(1, 0, 3). Найти длину высоты, опущенной из конца вектора на плоскость векторов и. Решение. h 73
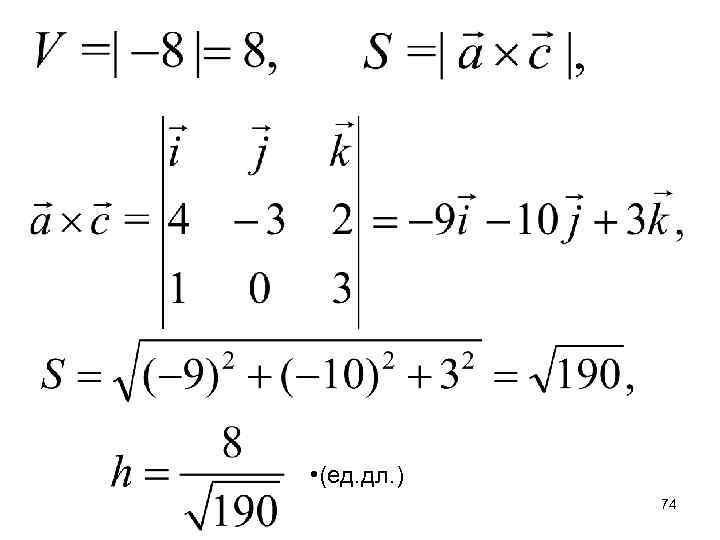 • (ед. дл. ) 74
• (ед. дл. ) 74


