2. Пример парной линейной регрессии.pptx
- Количество слайдов: 35
 Пример парной линейной регрессии
Пример парной линейной регрессии
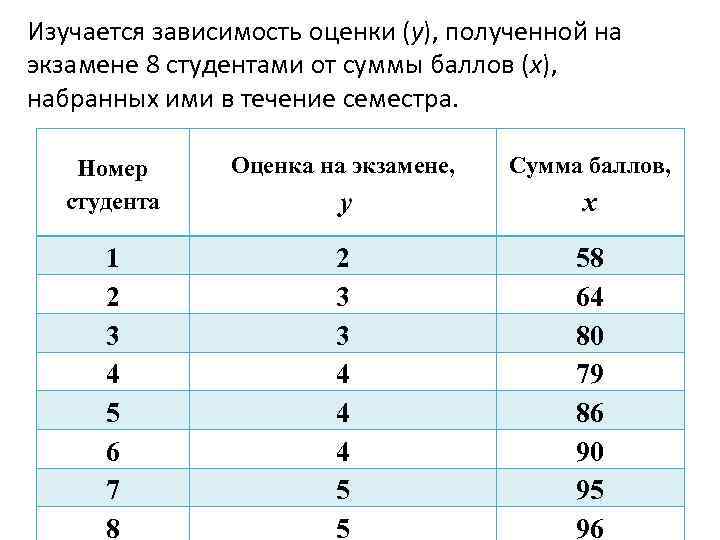 Изучается зависимость оценки (у), полученной на экзамене 8 студентами от суммы баллов (x), набранных ими в течение семестра. Номер студента Оценка на экзамене, Сумма баллов, у x 1 2 3 4 5 6 7 8 2 3 3 4 4 4 5 5 58 64 80 79 86 90 95 96
Изучается зависимость оценки (у), полученной на экзамене 8 студентами от суммы баллов (x), набранных ими в течение семестра. Номер студента Оценка на экзамене, Сумма баллов, у x 1 2 3 4 5 6 7 8 2 3 3 4 4 4 5 5 58 64 80 79 86 90 95 96
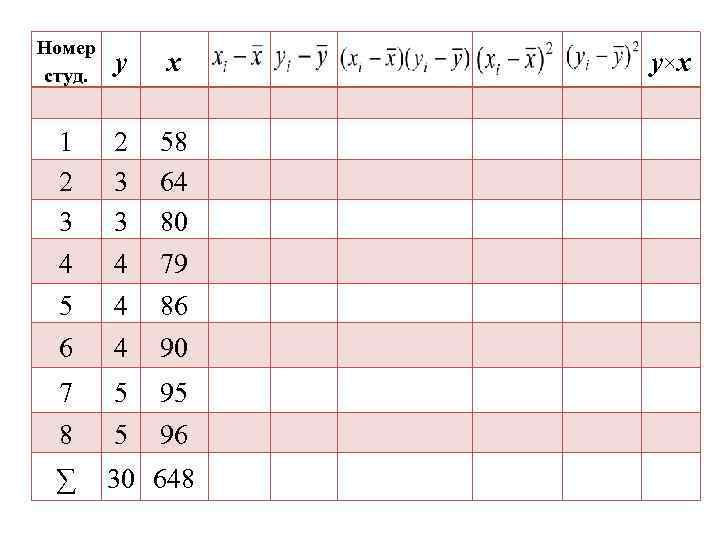 Номер студ. у x 1 2 3 3 58 64 80 4 4 79 5 4 86 6 4 90 7 5 95 8 5 96 ∑ 30 648 y×x
Номер студ. у x 1 2 3 3 58 64 80 4 4 79 5 4 86 6 4 90 7 5 95 8 5 96 ∑ 30 648 y×x
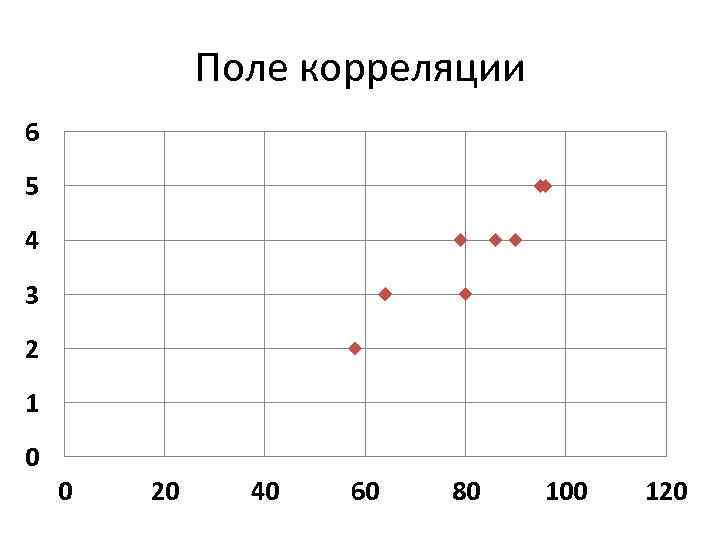 Поле корреляции 6 5 4 3 2 1 0 0 20 40 60 80 100 120
Поле корреляции 6 5 4 3 2 1 0 0 20 40 60 80 100 120
 Коэффициент парной линейной корреляции
Коэффициент парной линейной корреляции
 Коэффициент парной линейной корреляции
Коэффициент парной линейной корреляции
 Коэффициент парной линейной корреляции
Коэффициент парной линейной корреляции
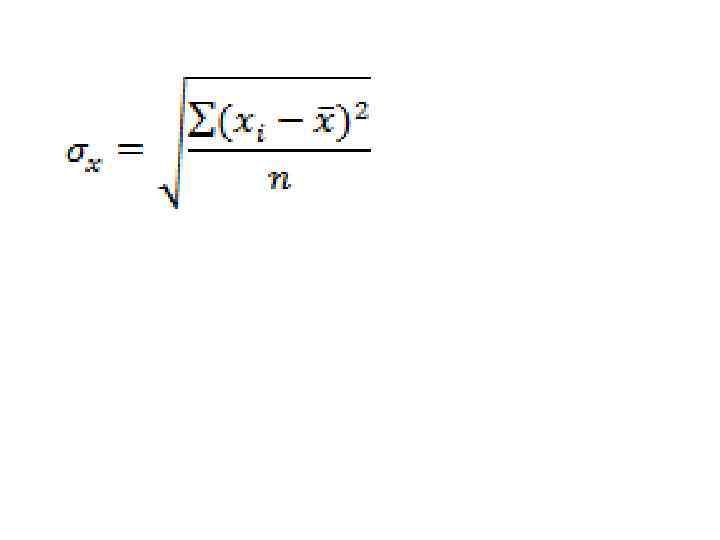
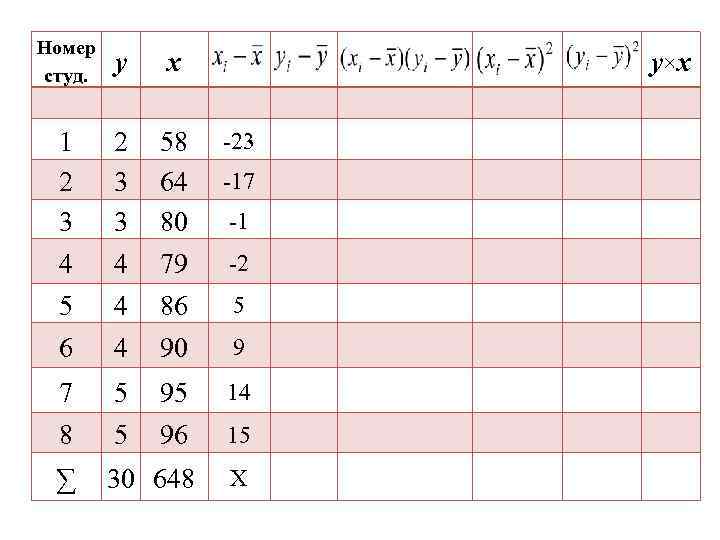 Номер студ. у x 1 2 3 3 58 64 80 -23 4 4 79 -2 5 4 86 5 6 4 90 9 7 5 95 14 8 5 96 15 ∑ 30 648 Х y×x -17 -1
Номер студ. у x 1 2 3 3 58 64 80 -23 4 4 79 -2 5 4 86 5 6 4 90 9 7 5 95 14 8 5 96 15 ∑ 30 648 Х y×x -17 -1
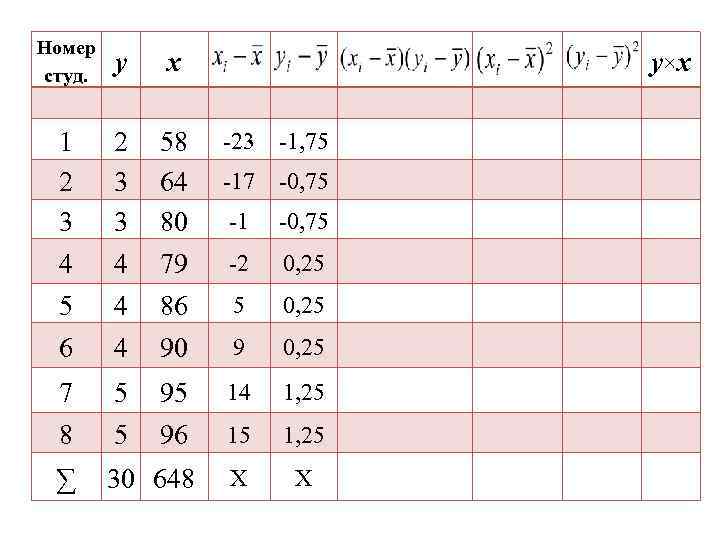 Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 -1 -0, 75 4 4 79 -2 0, 25 5 4 86 5 0, 25 6 4 90 9 0, 25 7 5 95 14 1, 25 8 5 96 15 1, 25 ∑ 30 648 Х Х y×x -17 -0, 75
Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 -1 -0, 75 4 4 79 -2 0, 25 5 4 86 5 0, 25 6 4 90 9 0, 25 7 5 95 14 1, 25 8 5 96 15 1, 25 ∑ 30 648 Х Х y×x -17 -0, 75
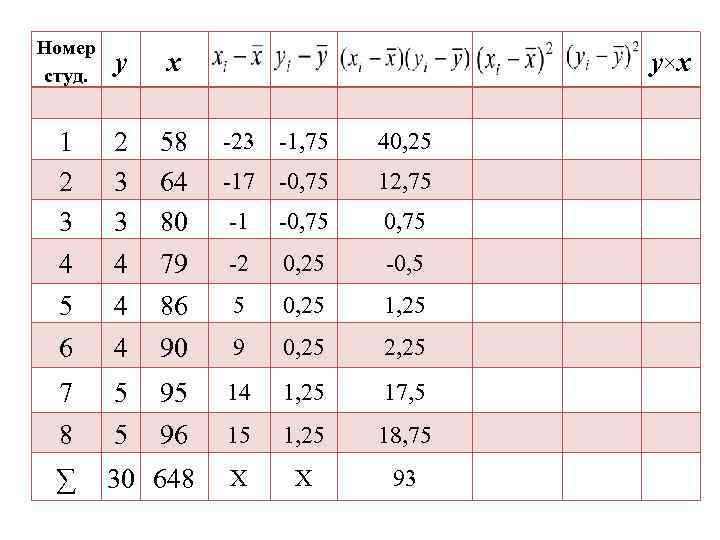 Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 40, 25 -17 -0, 75 12, 75 -1 -0, 75 4 4 79 -2 0, 25 -0, 5 5 4 86 5 0, 25 1, 25 6 4 90 9 0, 25 2, 25 7 5 95 14 1, 25 17, 5 8 5 96 15 1, 25 18, 75 ∑ 30 648 Х Х 93 y×x
Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 40, 25 -17 -0, 75 12, 75 -1 -0, 75 4 4 79 -2 0, 25 -0, 5 5 4 86 5 0, 25 1, 25 6 4 90 9 0, 25 2, 25 7 5 95 14 1, 25 17, 5 8 5 96 15 1, 25 18, 75 ∑ 30 648 Х Х 93 y×x
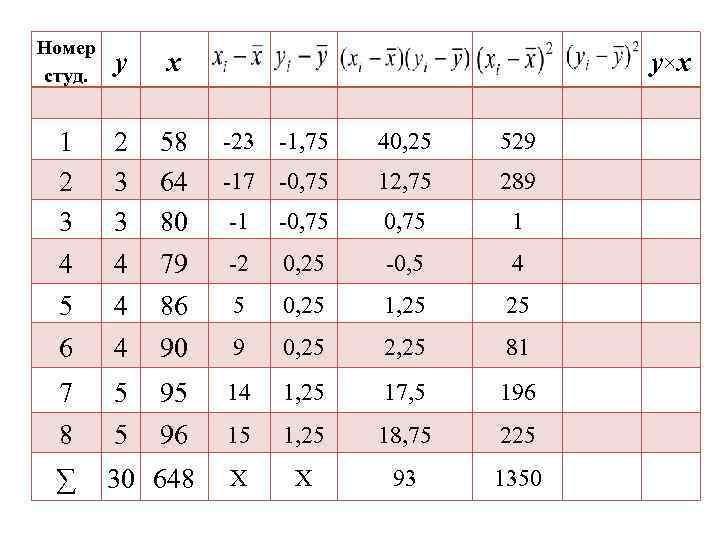 Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 40, 25 529 -17 -0, 75 12, 75 289 -1 -0, 75 1 4 4 79 -2 0, 25 -0, 5 4 86 5 0, 25 1, 25 25 6 4 90 9 0, 25 2, 25 81 7 5 95 14 1, 25 17, 5 196 8 5 96 15 1, 25 18, 75 225 ∑ 30 648 Х Х 93 1350 y×x
Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 40, 25 529 -17 -0, 75 12, 75 289 -1 -0, 75 1 4 4 79 -2 0, 25 -0, 5 4 86 5 0, 25 1, 25 25 6 4 90 9 0, 25 2, 25 81 7 5 95 14 1, 25 17, 5 196 8 5 96 15 1, 25 18, 75 225 ∑ 30 648 Х Х 93 1350 y×x
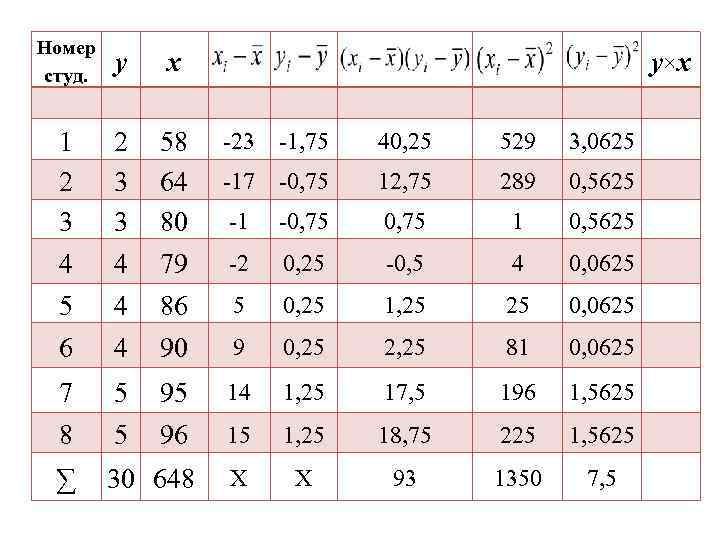 Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 40, 25 529 3, 0625 -17 -0, 75 12, 75 289 0, 5625 -1 -0, 75 1 0, 5625 4 4 79 -2 0, 25 -0, 5 4 0, 0625 5 4 86 5 0, 25 1, 25 25 0, 0625 6 4 90 9 0, 25 2, 25 81 0, 0625 7 5 95 14 1, 25 17, 5 196 1, 5625 8 5 96 15 1, 25 18, 75 225 1, 5625 ∑ 30 648 Х Х 93 1350 7, 5 y×x
Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 40, 25 529 3, 0625 -17 -0, 75 12, 75 289 0, 5625 -1 -0, 75 1 0, 5625 4 4 79 -2 0, 25 -0, 5 4 0, 0625 5 4 86 5 0, 25 1, 25 25 0, 0625 6 4 90 9 0, 25 2, 25 81 0, 0625 7 5 95 14 1, 25 17, 5 196 1, 5625 8 5 96 15 1, 25 18, 75 225 1, 5625 ∑ 30 648 Х Х 93 1350 7, 5 y×x
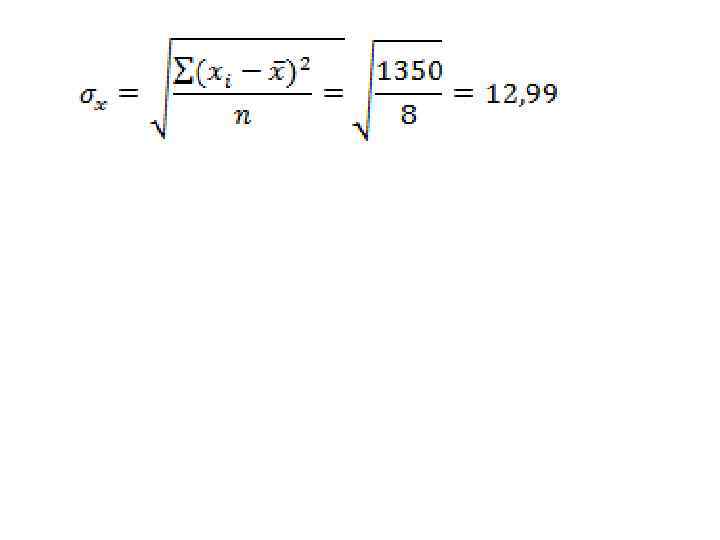
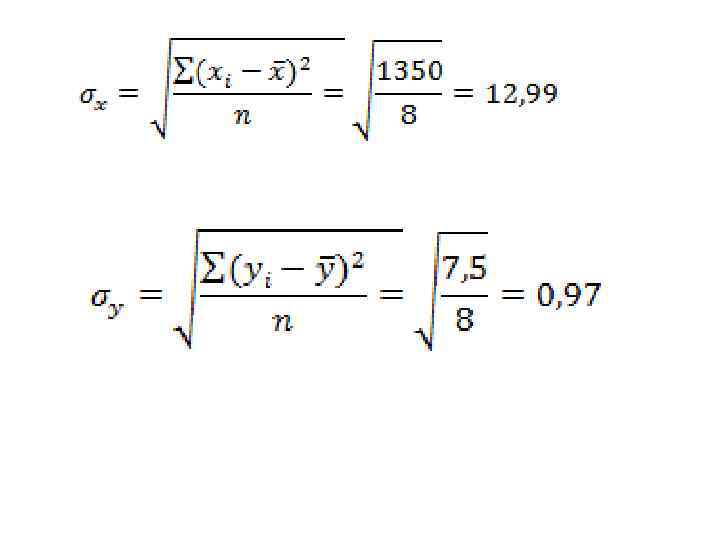
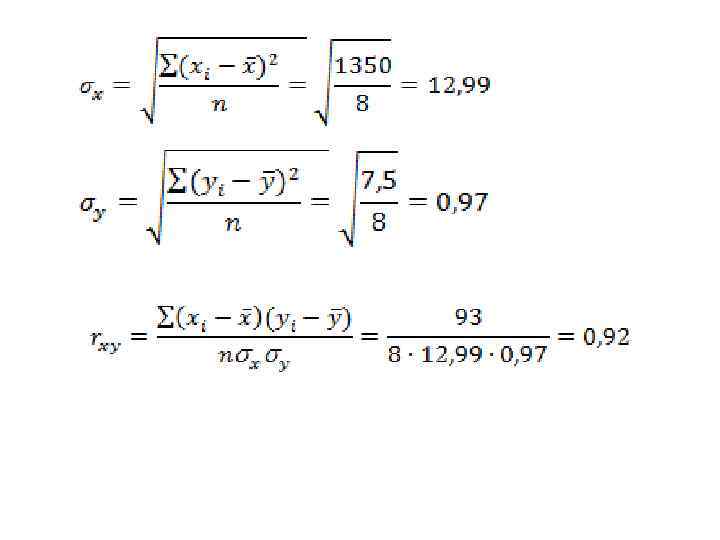
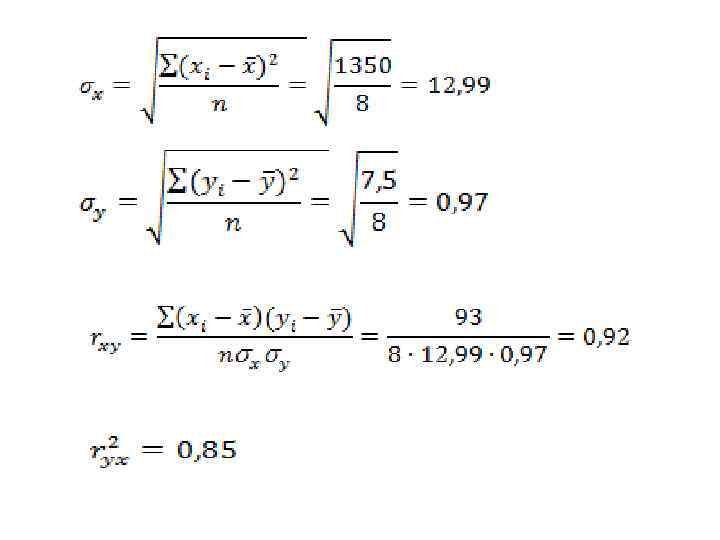
 Однородность исходных данных
Однородность исходных данных
 Однородность исходных данных
Однородность исходных данных
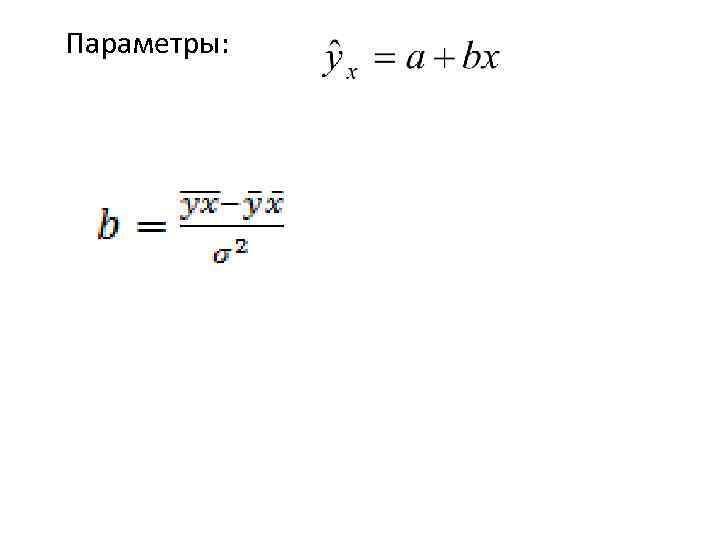 Параметры:
Параметры:
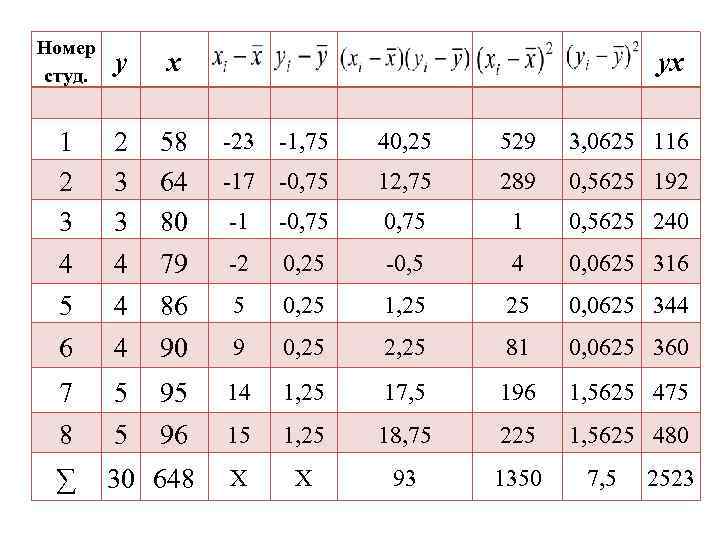 Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 40, 25 529 3, 0625 116 -17 -0, 75 12, 75 289 0, 5625 192 -1 -0, 75 1 0, 5625 240 4 4 79 -2 0, 25 -0, 5 4 0, 0625 316 5 4 86 5 0, 25 1, 25 25 0, 0625 344 6 4 90 9 0, 25 2, 25 81 0, 0625 360 7 5 95 14 1, 25 17, 5 196 1, 5625 475 8 5 96 15 1, 25 18, 75 225 1, 5625 480 ∑ 30 648 Х Х 93 1350 yx 7, 5 2523
Номер студ. у x 1 2 3 3 58 64 80 -23 -1, 75 40, 25 529 3, 0625 116 -17 -0, 75 12, 75 289 0, 5625 192 -1 -0, 75 1 0, 5625 240 4 4 79 -2 0, 25 -0, 5 4 0, 0625 316 5 4 86 5 0, 25 1, 25 25 0, 0625 344 6 4 90 9 0, 25 2, 25 81 0, 0625 360 7 5 95 14 1, 25 17, 5 196 1, 5625 475 8 5 96 15 1, 25 18, 75 225 1, 5625 480 ∑ 30 648 Х Х 93 1350 yx 7, 5 2523
 Параметры:
Параметры:
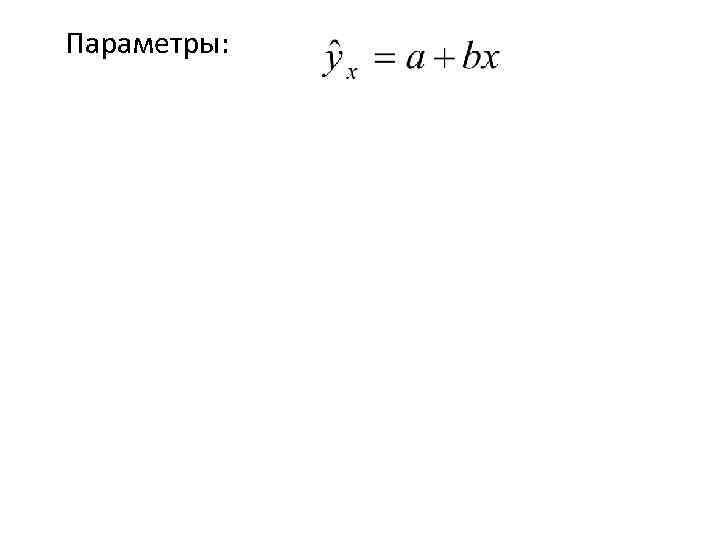 Параметры:
Параметры:
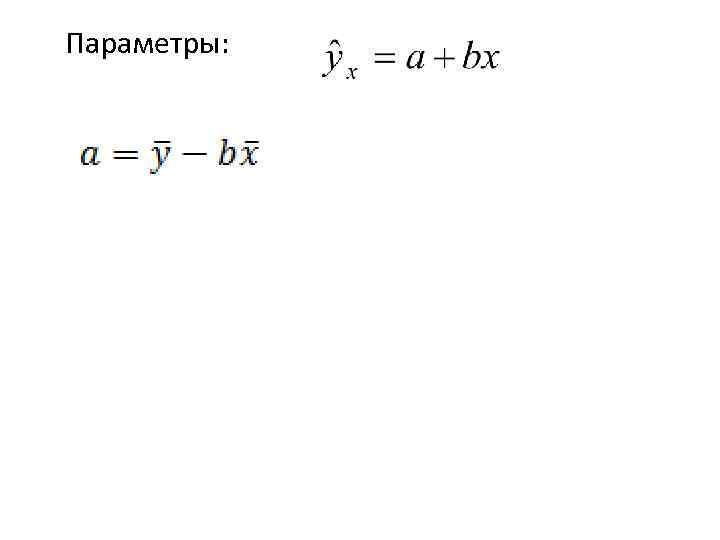 Параметры:
Параметры:
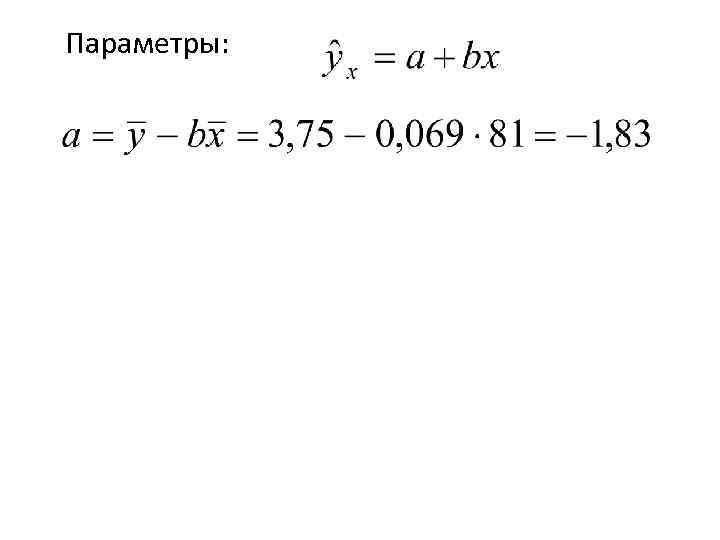 Параметры:
Параметры:
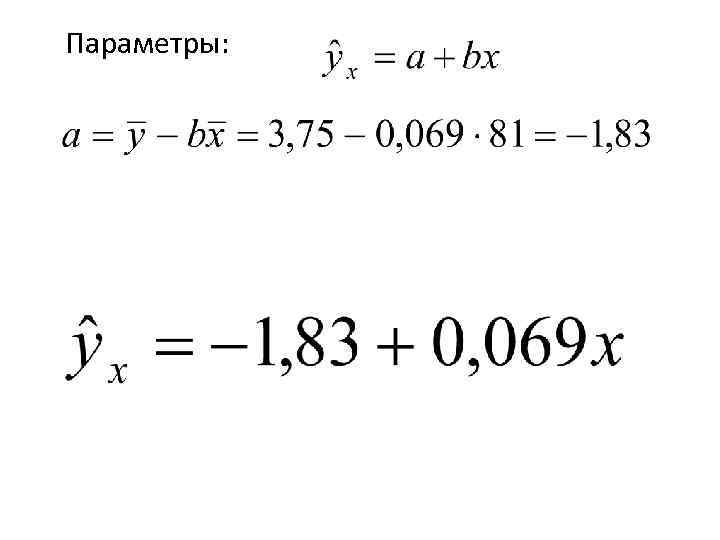 Параметры:
Параметры:
 Оценка влияния факторов на результативный признак
Оценка влияния факторов на результативный признак
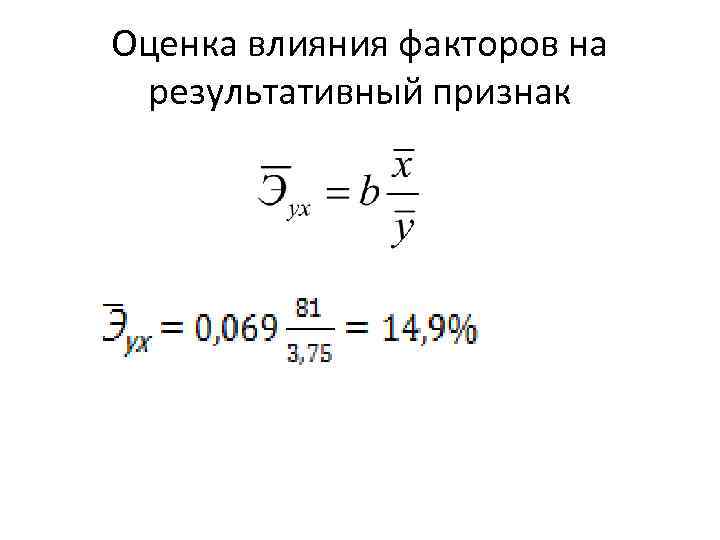 Оценка влияния факторов на результативный признак
Оценка влияния факторов на результативный признак
 Средняя относительная ошибка аппроксимации
Средняя относительная ошибка аппроксимации
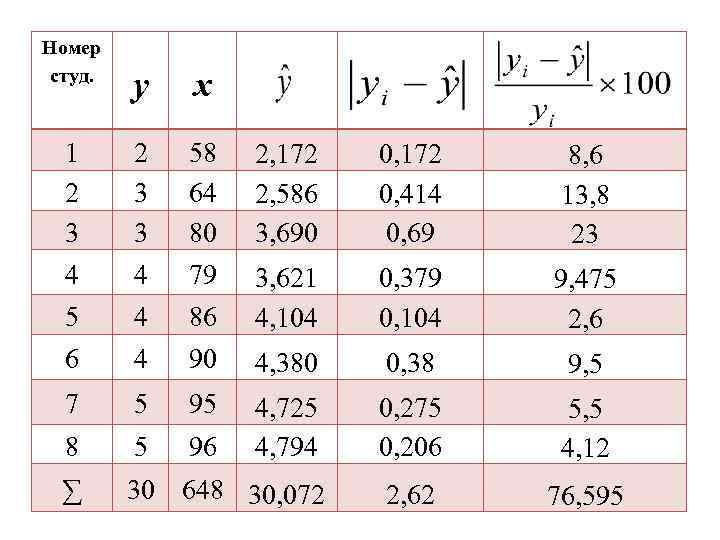 Номер студ. у x 1 2 3 3 58 64 80 2, 172 2, 586 3, 690 0, 172 0, 414 0, 69 8, 6 13, 8 23 4 4 79 5 4 86 3, 621 4, 104 0, 379 0, 104 9, 475 2, 6 6 4 90 4, 380 0, 38 9, 5 7 5 95 8 5 96 4, 725 4, 794 0, 275 0, 206 5, 5 4, 12 ∑ 30 648 30, 072 2, 62 76, 595
Номер студ. у x 1 2 3 3 58 64 80 2, 172 2, 586 3, 690 0, 172 0, 414 0, 69 8, 6 13, 8 23 4 4 79 5 4 86 3, 621 4, 104 0, 379 0, 104 9, 475 2, 6 6 4 90 4, 380 0, 38 9, 5 7 5 95 8 5 96 4, 725 4, 794 0, 275 0, 206 5, 5 4, 12 ∑ 30 648 30, 072 2, 62 76, 595
 Средняя относительная ошибка аппроксимации
Средняя относительная ошибка аппроксимации
 Расчет показателей регрессии и корреляции с помощью пакета анализа в Excel 1. Выбрать Данные → Анализ данных → Регрессия
Расчет показателей регрессии и корреляции с помощью пакета анализа в Excel 1. Выбрать Данные → Анализ данных → Регрессия
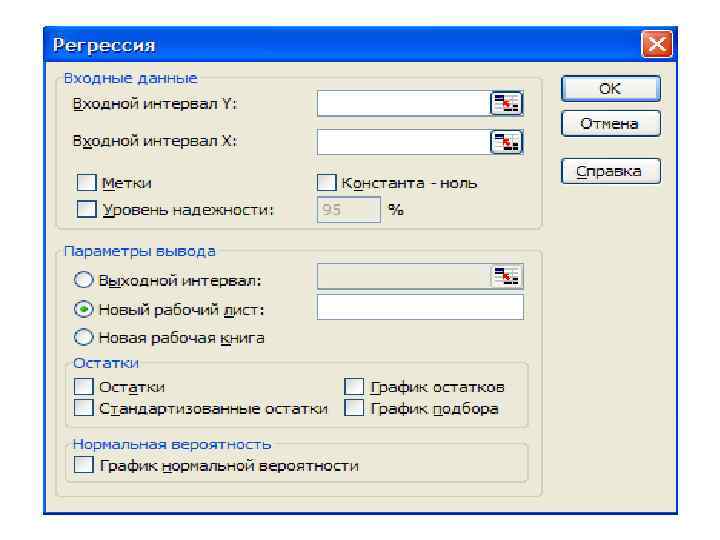
 Расчет показателей регрессии и корреляции с помощью пакета анализа в Excel 1. Выбрать Данные → Анализ данных → Регрессия. 2. В диалоговом окне Регрессия сделать следующее: • Входной интервал Y, - водится ссылка на диапазон ячеек, содержащий данные результативного признака. • Входной интервал X, - водится ссылка на диапазон ячеек, содержащий данные факторного признака. • Установить флажок Метки, если первая строка содержит название столбцов, • Ввести в окне редактирование Выходной интервал номер свободной ячейки на рабочем листе. • нажать кнопку ОК.
Расчет показателей регрессии и корреляции с помощью пакета анализа в Excel 1. Выбрать Данные → Анализ данных → Регрессия. 2. В диалоговом окне Регрессия сделать следующее: • Входной интервал Y, - водится ссылка на диапазон ячеек, содержащий данные результативного признака. • Входной интервал X, - водится ссылка на диапазон ячеек, содержащий данные факторного признака. • Установить флажок Метки, если первая строка содержит название столбцов, • Ввести в окне редактирование Выходной интервал номер свободной ячейки на рабочем листе. • нажать кнопку ОК.
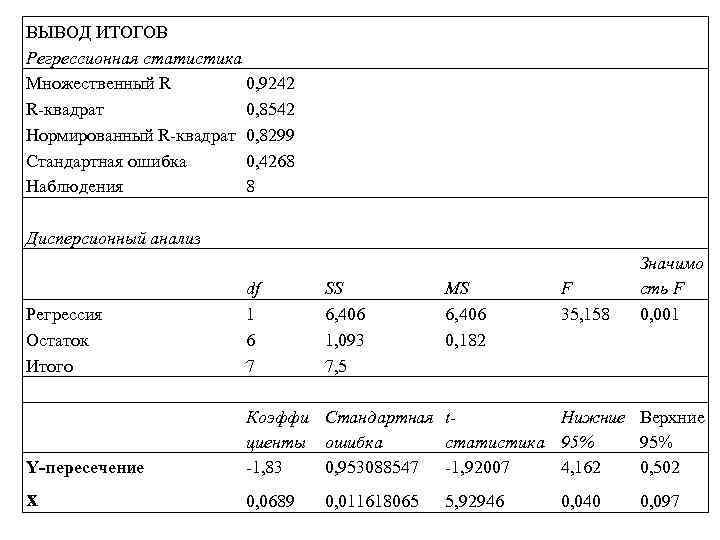 ВЫВОД ИТОГОВ Регрессионная статистика Множественный R 0, 9242 R-квадрат 0, 8542 Нормированный R-квадрат 0, 8299 Стандартная ошибка 0, 4268 Наблюдения 8 Дисперсионный анализ SS 6, 406 1, 093 7, 5 F 35, 158 Регрессия Остаток Итого df 1 6 7 Y-пересечение Коэффи Стандартная t. Нижние Верхние циенты ошибка статистика 95% -1, 83 0, 953088547 -1, 92007 4, 162 0, 502 x 0, 0689 0, 011618065 MS 6, 406 0, 182 Значимо сть F 0, 001 5, 92946 0, 040 0, 097
ВЫВОД ИТОГОВ Регрессионная статистика Множественный R 0, 9242 R-квадрат 0, 8542 Нормированный R-квадрат 0, 8299 Стандартная ошибка 0, 4268 Наблюдения 8 Дисперсионный анализ SS 6, 406 1, 093 7, 5 F 35, 158 Регрессия Остаток Итого df 1 6 7 Y-пересечение Коэффи Стандартная t. Нижние Верхние циенты ошибка статистика 95% -1, 83 0, 953088547 -1, 92007 4, 162 0, 502 x 0, 0689 0, 011618065 MS 6, 406 0, 182 Значимо сть F 0, 001 5, 92946 0, 040 0, 097


