Пример. Найти частные производные функции y x


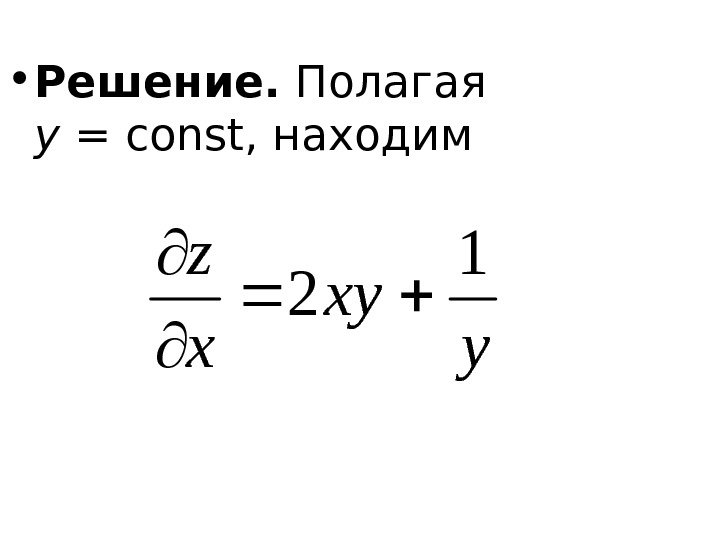


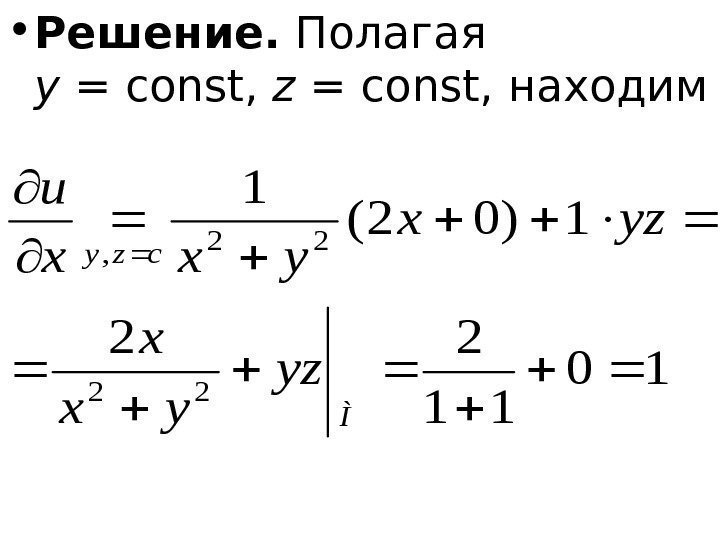
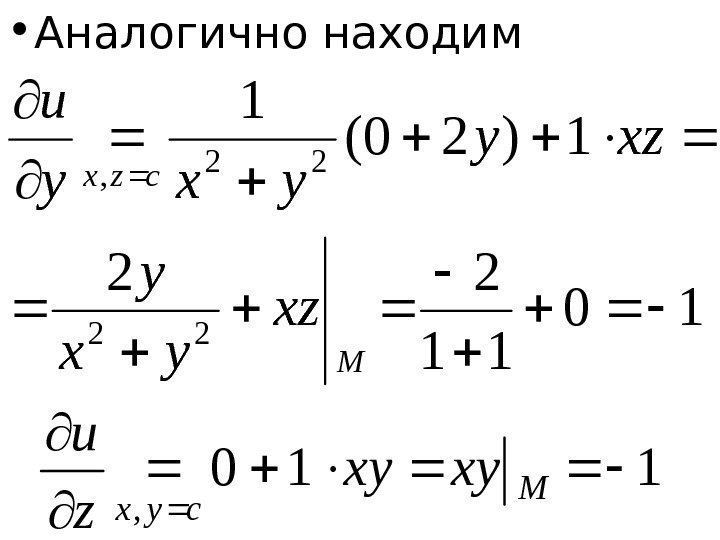









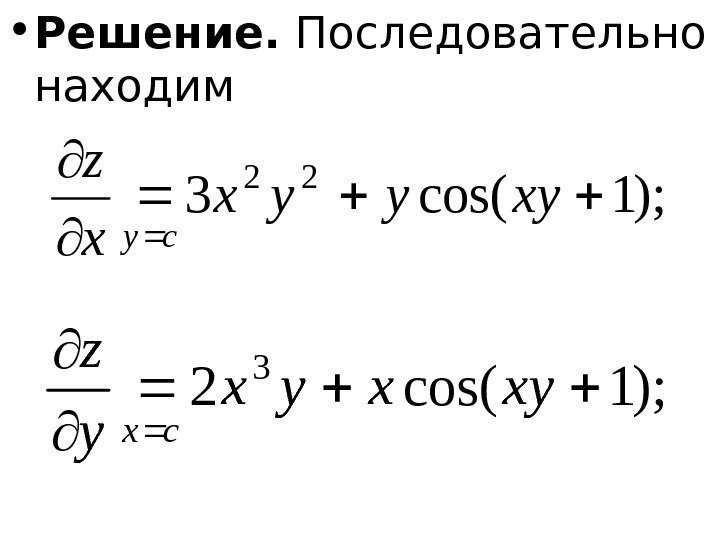
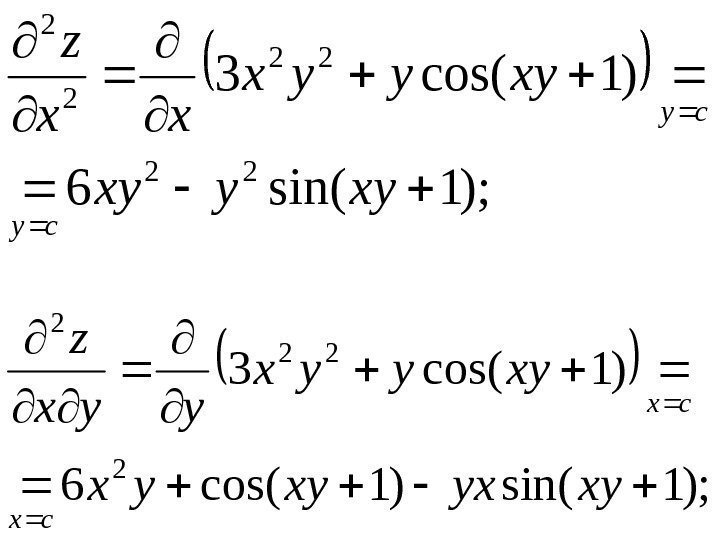
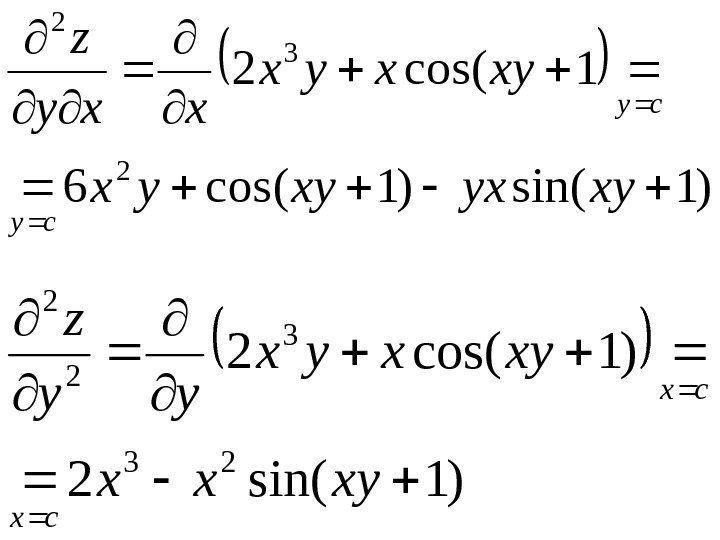




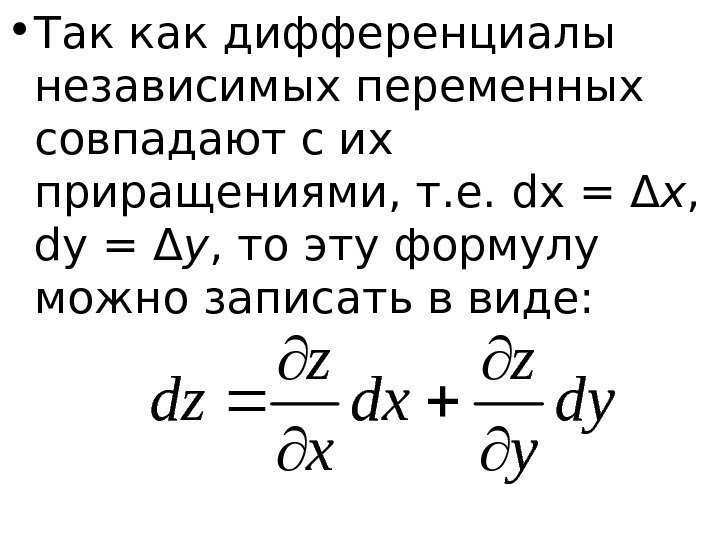






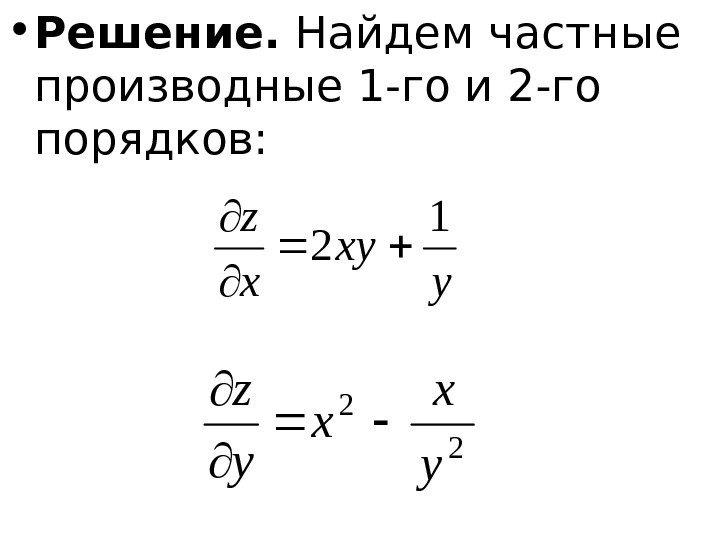
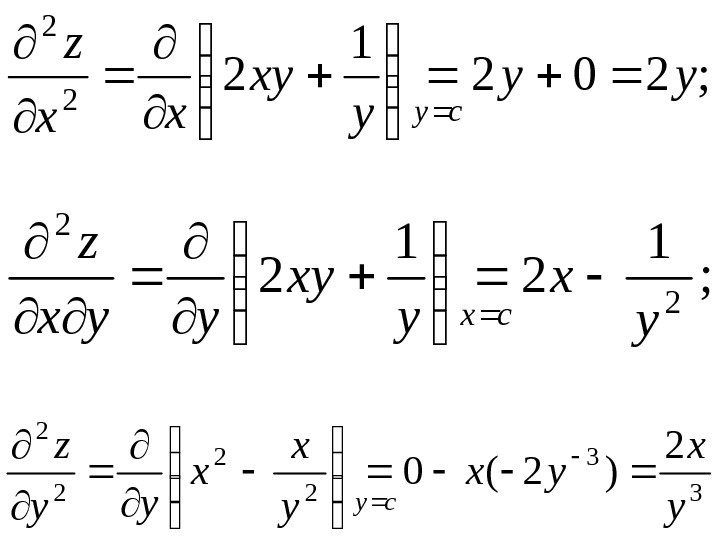






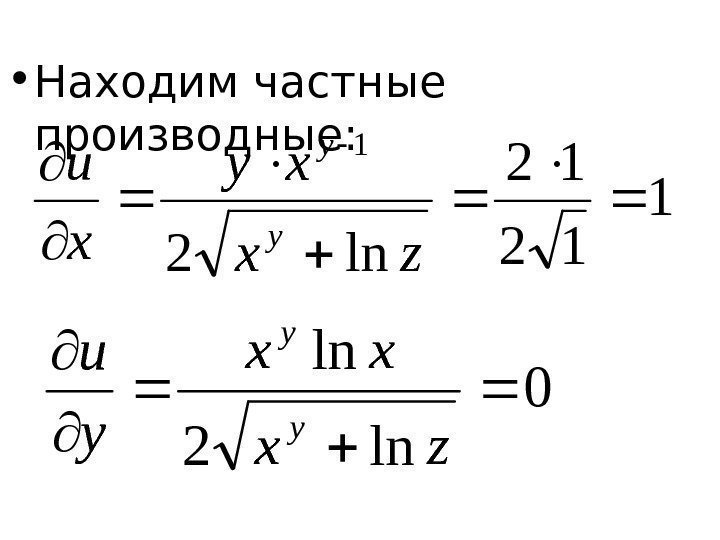
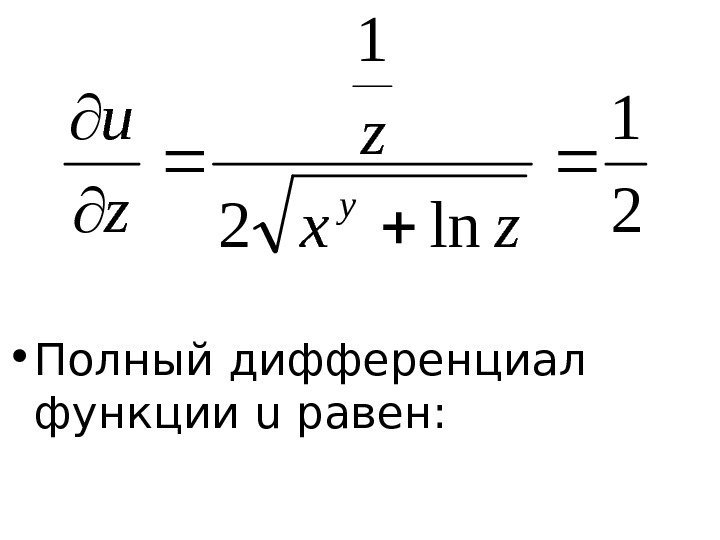
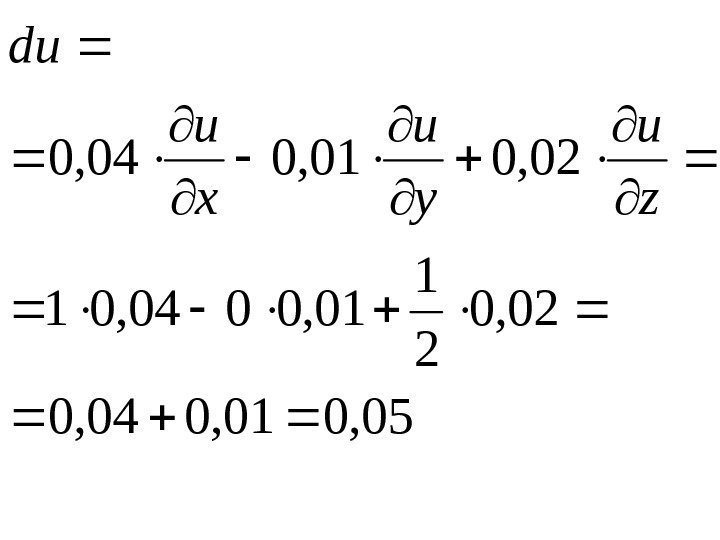




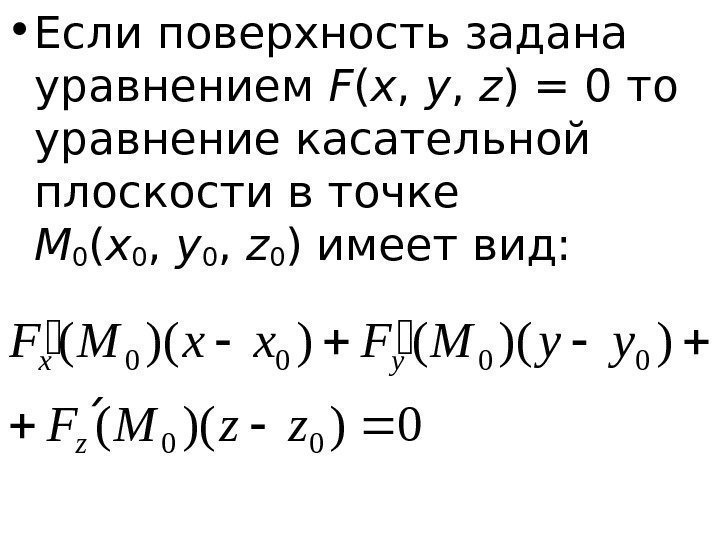






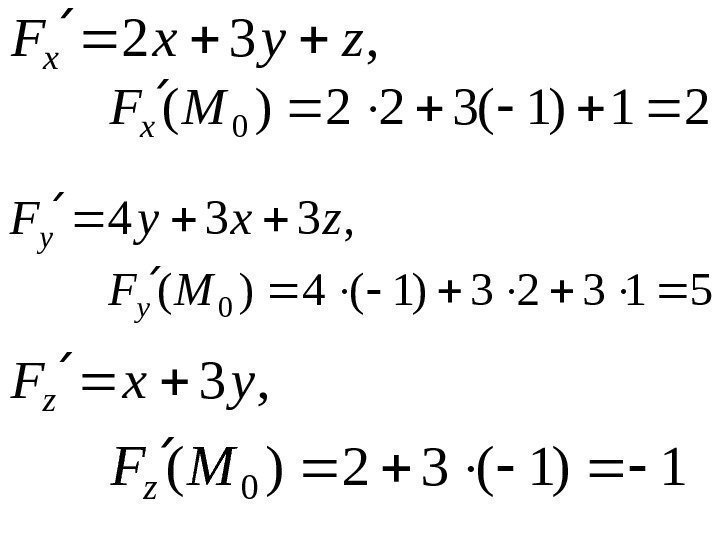
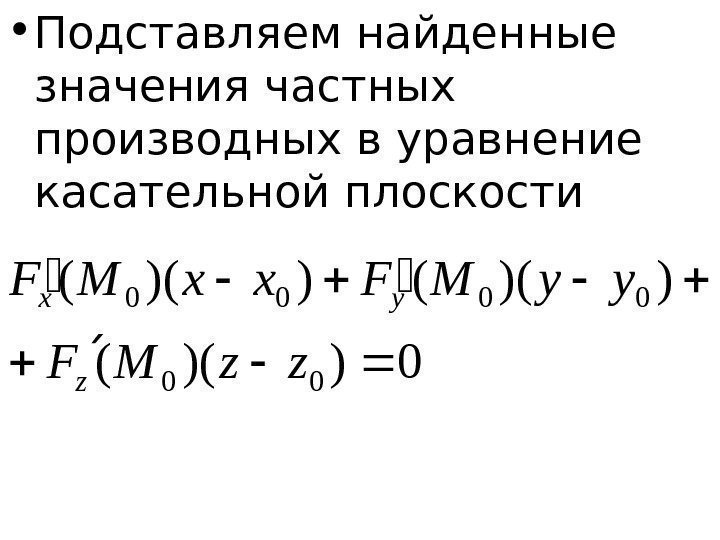











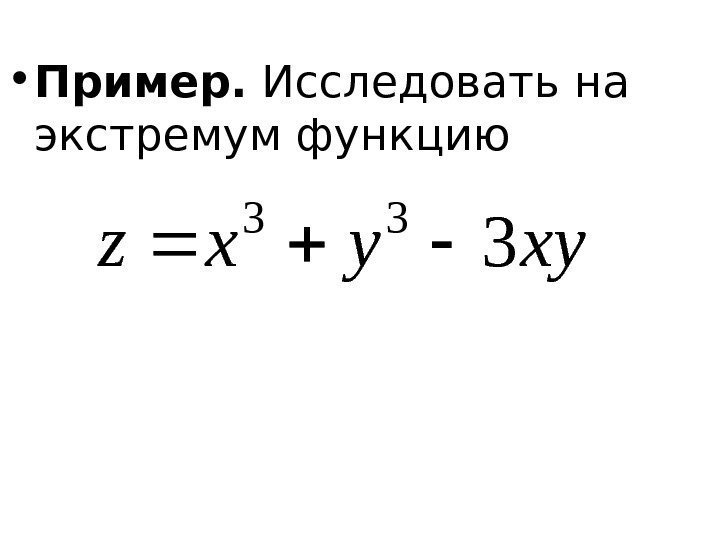







fnp_2.ppt
- Размер: 455.5 Кб
- Автор:
- Количество слайдов: 79
Описание презентации Пример. Найти частные производные функции y x по слайдам
 • Пример. Найти частные производные функции y x yxz
• Пример. Найти частные производные функции y x yxz
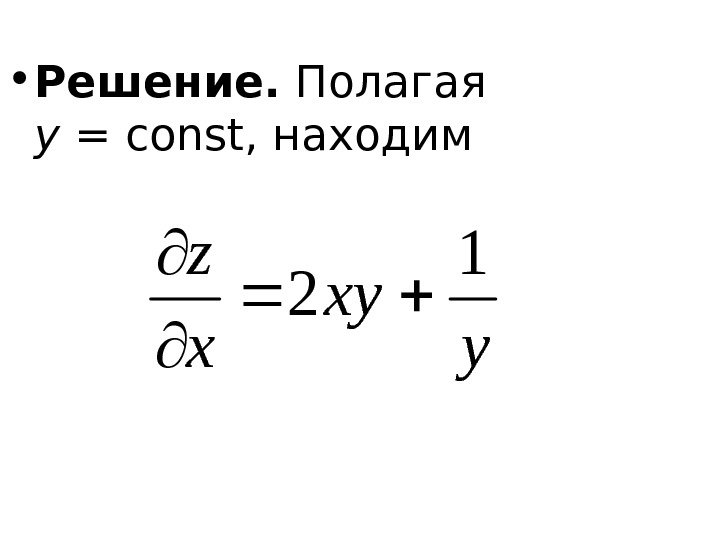 • Решение. Полагая y =const , находимy xy x z
• Решение. Полагая y =const , находимy xy x z
 • Полагая x =const , находим 2 2 ) 1 (1 y x x y xx y z
• Полагая x =const , находим 2 2 ) 1 (1 y x x y xx y z
 • Пример. Найти значения частных производных функции в точке M (1, – 1, 0). xyzyxu)ln(
• Пример. Найти значения частных производных функции в точке M (1, – 1, 0). xyzyxu)ln(
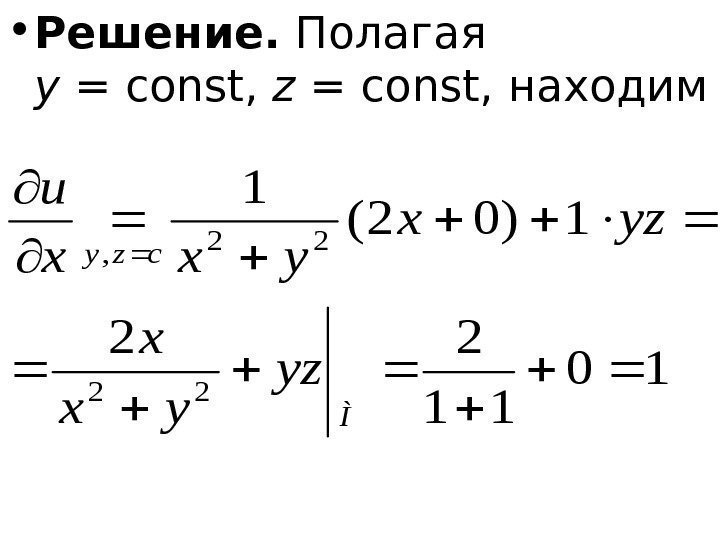 • Решение. Полагая y = const , z = const , находим 10 11 22 1)02( 1 22 22 , Ì czy yz yx x yzx yxx u
• Решение. Полагая y = const , z = const , находим 10 11 22 1)02( 1 22 22 , Ì czy yz yx x yzx yxx u
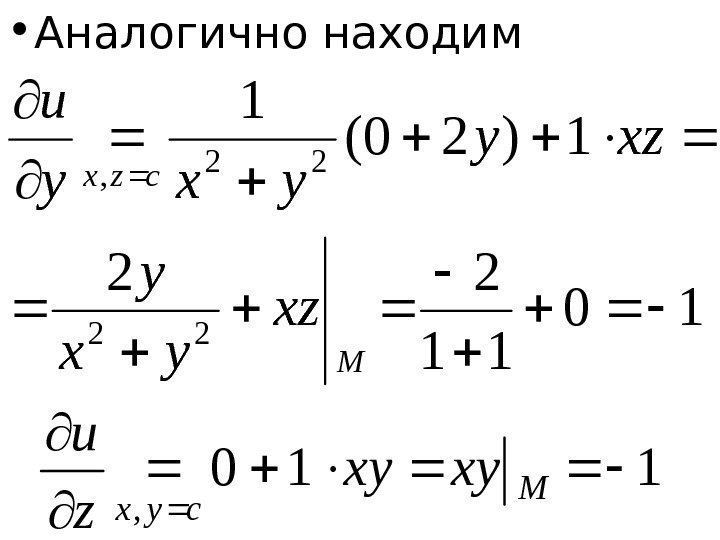 • Аналогично находим 10 11 22 1)20( 1 22 22 , M czx xz yx y xzy yxy u 110 , M cyx xyxy z u
• Аналогично находим 10 11 22 1)20( 1 22 22 , M czx xz yx y xzy yxy u 110 , M cyx xyxy z u
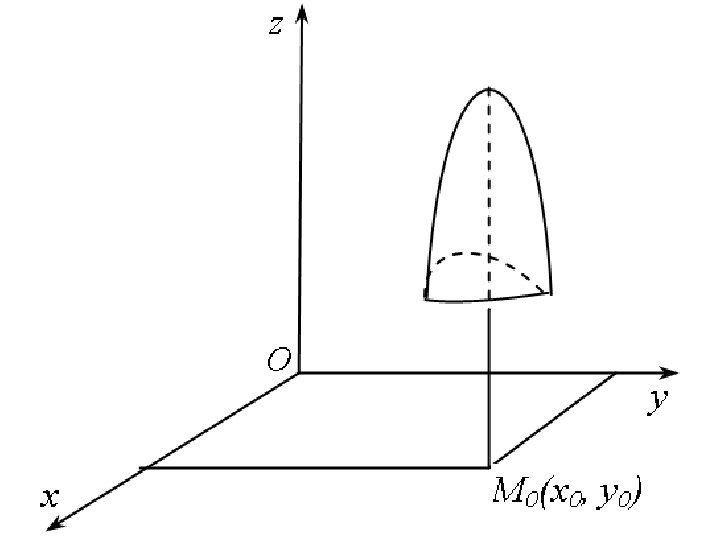
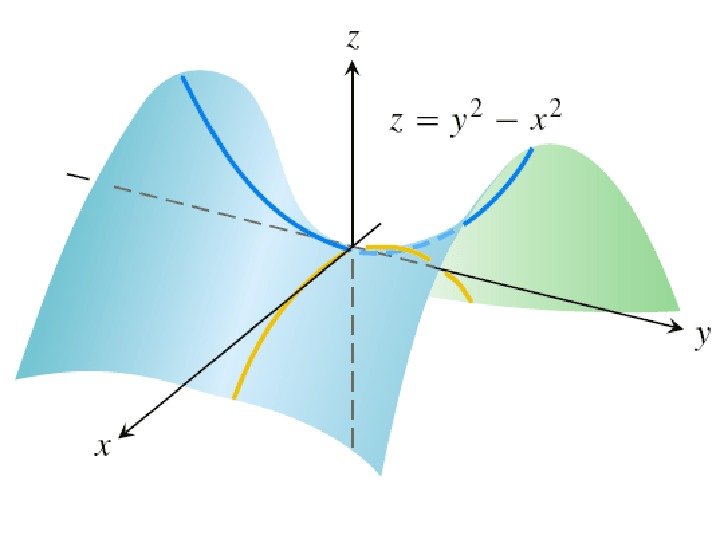
 • Геометрическим смыслом частной производной (например, ) является тангенс угла наклона касательной, проведенной в точке M 0 ( x 0 , y 0 , z 0 ) к сечению поверхности плоскостью у = у 0. xz
• Геометрическим смыслом частной производной (например, ) является тангенс угла наклона касательной, проведенной в точке M 0 ( x 0 , y 0 , z 0 ) к сечению поверхности плоскостью у = у 0. xz
 • Предположим, что функция z = f ( x , y ) имеет непрерывные частные производные), (yxf x z x ), (yxf y z y
• Предположим, что функция z = f ( x , y ) имеет непрерывные частные производные), (yxf x z x ), (yxf y z y
 • Эти производные в свою очередь являются функциями независимых переменных x и y. Будем называть и частными производными 1 — го порядка. ), (yxf x ), (yxf y
• Эти производные в свою очередь являются функциями независимых переменных x и y. Будем называть и частными производными 1 — го порядка. ), (yxf x ), (yxf y
 • Частными производными 2 -го порядка называются частные производные от частных производных 1 -го порядка. • Для функции z = f ( x , y ) двух переменных можно найти четыре частные производные 2 -го порядка, которые обозна-чаются следующим обр-м:
• Частными производными 2 -го порядка называются частные производные от частных производных 1 -го порядка. • Для функции z = f ( x , y ) двух переменных можно найти четыре частные производные 2 -го порядка, которые обозна-чаются следующим обр-м:

 • В общем случае смешанные частные производные могут не совпадать, однако для них справедлива теорема: • Теорема. Если смешанные частные производные и непрерывны в некоторой точке M ( x , y ) , то они равны, т. е. xyfyxf ), (yxfyxf yxxy
• В общем случае смешанные частные производные могут не совпадать, однако для них справедлива теорема: • Теорема. Если смешанные частные производные и непрерывны в некоторой точке M ( x , y ) , то они равны, т. е. xyfyxf ), (yxfyxf yxxy
 • Ч астными производными n – го порядка называются частные производные от частных производных ( n – 1)– го порядка. • Их обозначают и т. д. 221 , , yx z x z n n n
• Ч астными производными n – го порядка называются частные производные от частных производных ( n – 1)– го порядка. • Их обозначают и т. д. 221 , , yx z x z n n n
 • Частные производные любого порядка, взятые по различным переменным, называются смешанными.
• Частные производные любого порядка, взятые по различным переменным, называются смешанными.
 • Пример. Найти частные производные 2 -го порядка функции )1 sin( 23 xyyxz
• Пример. Найти частные производные 2 -го порядка функции )1 sin( 23 xyyxz
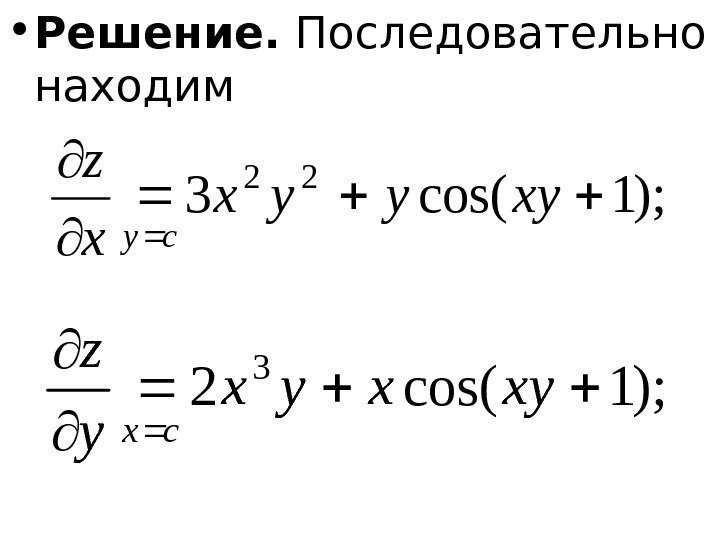 • Решение. Последовательно находим); 1 cos(3 22 xyyyx x z cy ); 1 cos(2 3 xyxyx y z cx
• Решение. Последовательно находим); 1 cos(3 22 xyyyx x z cy ); 1 cos(2 3 xyxyx y z cx
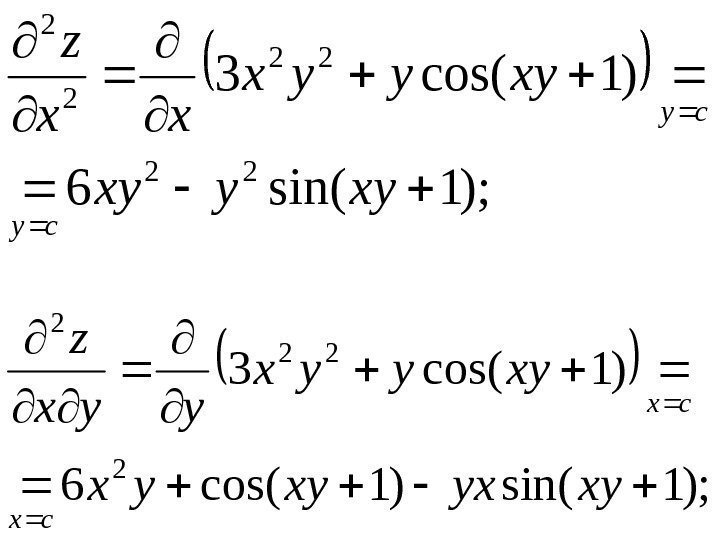 ); 1 sin(6 )1 cos(3 22 22 2 2 xyyxy xyyyx xx z cy cy ); 1 sin()1 cos(6 )1 cos(3 2 22 2 xyyx xyyyx z cx cx
); 1 sin(6 )1 cos(3 22 22 2 2 xyyxy xyyyx xx z cy cy ); 1 sin()1 cos(6 )1 cos(3 2 22 2 xyyx xyyyx z cx cx
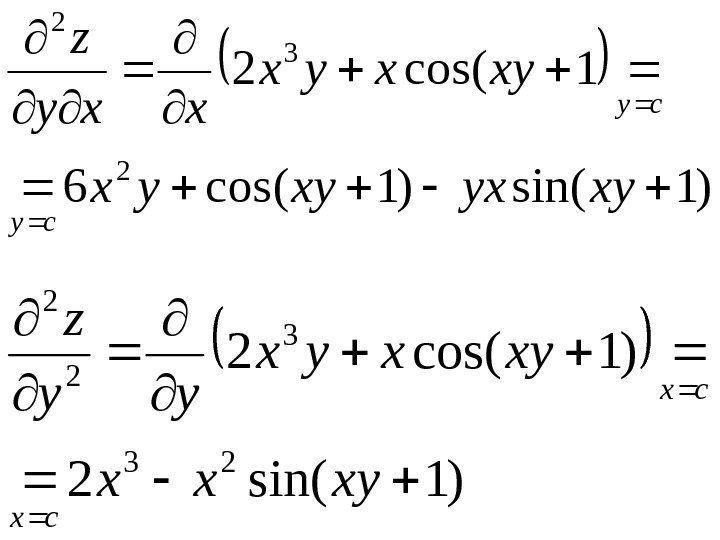 )1 sin()1 cos(6 1 cos(2 2 3 2 xyyx xyxyx xxy z cy cy )1 sin(2 )1 cos(2 23 3 2 2 xyxx xyxyx yy z cx cx
)1 sin()1 cos(6 1 cos(2 2 3 2 xyyx xyxyx xxy z cy cy )1 sin(2 )1 cos(2 23 3 2 2 xyxx xyxyx yy z cx cx
 § 5. Дифференциал функции нескольких переменных
§ 5. Дифференциал функции нескольких переменных
 • Рассмотрим функцию z = f ( x , y ). Дадим аргументу x приращение Δ x , а аргументу y приращение Δ y. Тогда z получит приращение которое называется полным приращением функции z. ), (yxfyyxxfz
• Рассмотрим функцию z = f ( x , y ). Дадим аргументу x приращение Δ x , а аргументу y приращение Δ y. Тогда z получит приращение которое называется полным приращением функции z. ), (yxfyyxxfz
 • Предположим, что f ( x , y ) в точке M ( x , y ) имеет непрерывные частные производные.
• Предположим, что f ( x , y ) в точке M ( x , y ) имеет непрерывные частные производные.
 • Определение. Дифференциалом 1 -го порядка функции z = f ( x , y ) называется главная часть полного приращения Δ z этой функции, линейная относительно Δ x и Δ y , обозначается символом dz или df и вычисляется по формуле y y z x x z zd
• Определение. Дифференциалом 1 -го порядка функции z = f ( x , y ) называется главная часть полного приращения Δ z этой функции, линейная относительно Δ x и Δ y , обозначается символом dz или df и вычисляется по формуле y y z x x z zd
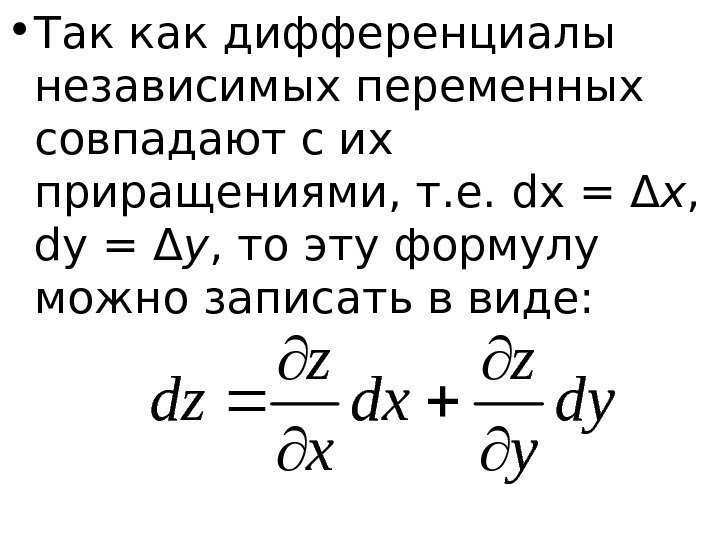 • Так как дифференциалы независимых переменных совпадают с их приращениями, т. е. dx = Δ x , dy = Δ y , то эту формулу можно записать в виде: dy y z dx x z zd
• Так как дифференциалы независимых переменных совпадают с их приращениями, т. е. dx = Δ x , dy = Δ y , то эту формулу можно записать в виде: dy y z dx x z zd
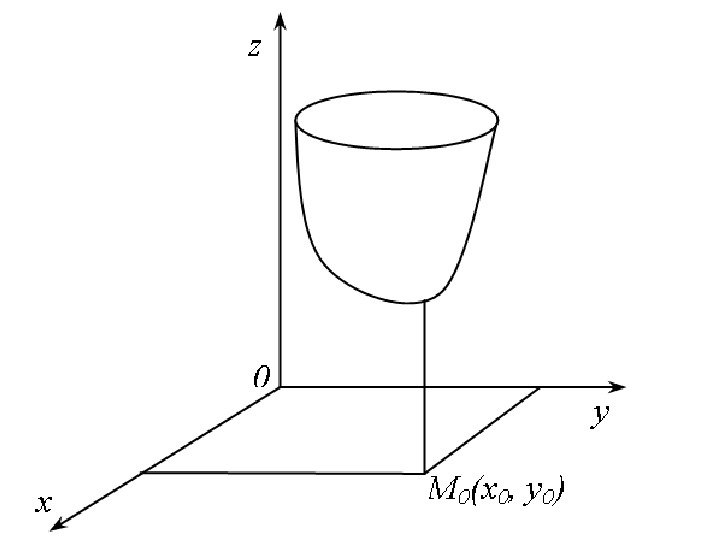
 • Геометрическим смыслом полного дифференциала функции двух переменных f ( x , y ) в точке (х 0 , у 0 ) является приращение аппликаты (координаты z ) касательной плоскости к поверхности при переходе от точки (х 0 , у 0 ) к точке (х 0 + х, у 0 + у).
• Геометрическим смыслом полного дифференциала функции двух переменных f ( x , y ) в точке (х 0 , у 0 ) является приращение аппликаты (координаты z ) касательной плоскости к поверхности при переходе от точки (х 0 , у 0 ) к точке (х 0 + х, у 0 + у).
 • Геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
• Геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
 • Дифференциалом 2 -го порядка функции z = f ( x , y ) называется дифференциал от ее дифференциала 1 -го порядка и обозначается)(zzddd
• Дифференциалом 2 -го порядка функции z = f ( x , y ) называется дифференциал от ее дифференциала 1 -го порядка и обозначается)(zzddd
 • Если все частные производные 2 -го порядка функции z = f ( x , y ) непрерывны, то имеет место формула: 2 2 2 y y z yx yx z x x z zddddd
• Если все частные производные 2 -го порядка функции z = f ( x , y ) непрерывны, то имеет место формула: 2 2 2 y y z yx yx z x x z zddddd
 • Аналогично определяется дифференциал n –го порядка: )d(dd 1 zz-nn
• Аналогично определяется дифференциал n –го порядка: )d(dd 1 zz-nn
 • Пример. Найти дифференциалы 1 -го и 2 -го порядков функции y x yz 2 x
• Пример. Найти дифференциалы 1 -го и 2 -го порядков функции y x yz 2 x
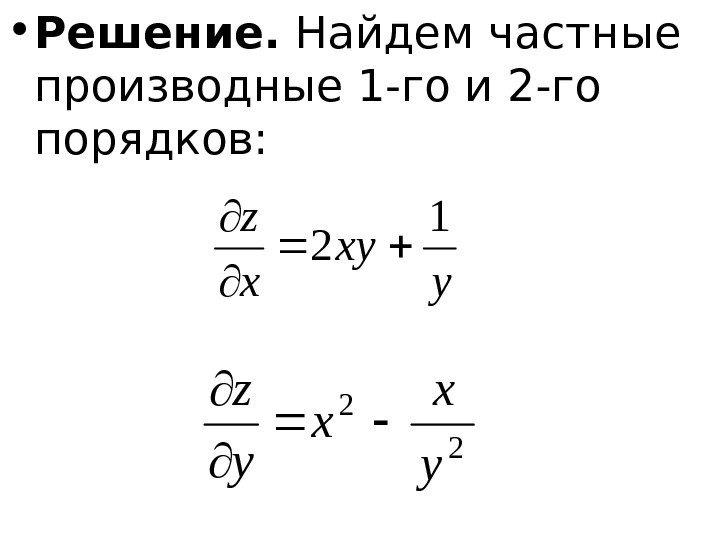 • Решение. Найдем частные производные 1 -го и 2 -го порядков: y yx x z 1 2 2 2 y x x y z
• Решение. Найдем частные производные 1 -го и 2 -го порядков: y yx x z 1 2 2 2 y x x y z
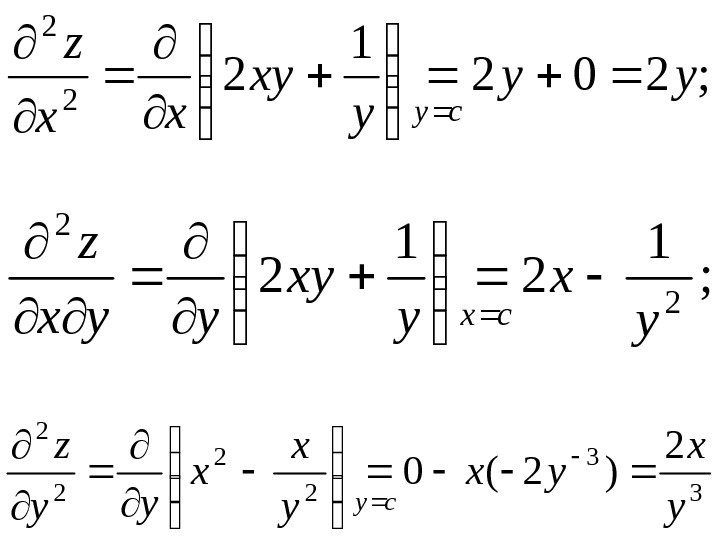 ; 202 1 2 2 2 yy y xy xx z cy ; 1 2 2 2 y xy yyx z cx 33 22 22 2 )2(0 y x yx y x x y y z cy
; 202 1 2 2 2 yy y xy xx z cy ; 1 2 2 2 y xy yyx z cx 33 22 22 2 )2(0 y x yx y x x y y z cy
 • Следовательно, дифференциалы 1 -го и 2 -го порядков запишутся в виде: dy y x xdx y xyz)() 1 2(d 2 2 2 32 222 ) 1 2(22 y y x yx y xxyzddddd
• Следовательно, дифференциалы 1 -го и 2 -го порядков запишутся в виде: dy y x xdx y xyz)() 1 2(d 2 2 2 32 222 ) 1 2(22 y y x yx y xxyzddddd
 Приближенные вычисления с помощью полного дифференциала
Приближенные вычисления с помощью полного дифференциала
 • Пусть функция f ( x , y ) дифференцируема в точке (х, у). Найдем полное приращение этой функции: ), (yxfyyxxfz zyxfyyxxf), (
• Пусть функция f ( x , y ) дифференцируема в точке (х, у). Найдем полное приращение этой функции: ), (yxfyyxxfz zyxfyyxxf), (
 • Если подставить в эту формулу выражение то получим приближенную формулу : y yf x xf dzz y y yxf x x yxf yyxxf ), (
• Если подставить в эту формулу выражение то получим приближенную формулу : y yf x xf dzz y y yxf x x yxf yyxxf ), (
 • Пример. Вычислить приближенно значение исходя из значения функции при x = 1, y = 2, z = 102, 1 ln 04, 1 99, 1 zxu y ln
• Пример. Вычислить приближенно значение исходя из значения функции при x = 1, y = 2, z = 102, 1 ln 04, 1 99, 1 zxu y ln
 • Решение. Из заданного выражения определим x = 1, 04 – 1 = 0, 04, y = 1, 99 – 2 = -0, 01, z = 1, 02 – 1 = 0, 02. • Найдем значение функции u ( x , y , z ) = 11 ln
• Решение. Из заданного выражения определим x = 1, 04 – 1 = 0, 04, y = 1, 99 – 2 = -0, 01, z = 1, 02 – 1 = 0, 02. • Найдем значение функции u ( x , y , z ) = 11 ln
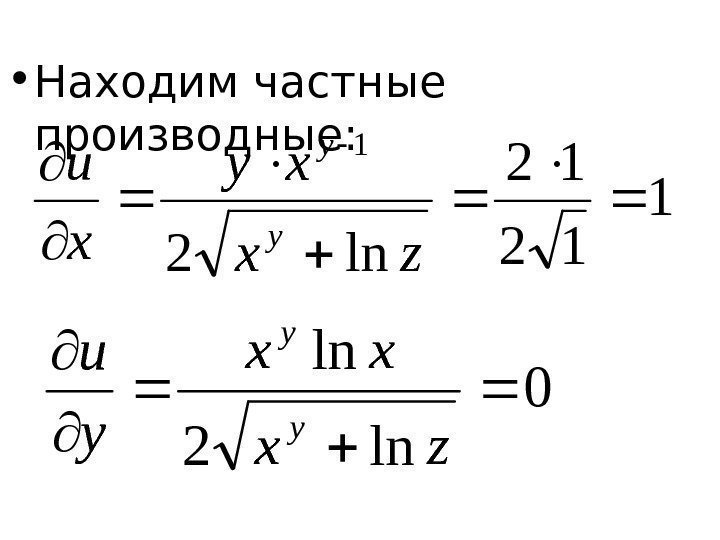 • Находим частные производные : 1 12 12 ln 2 1 zx xy x u y y 0 ln 2 ln zx xx y u y y
• Находим частные производные : 1 12 12 ln 2 1 zx xy x u y y 0 ln 2 ln zx xx y u y y
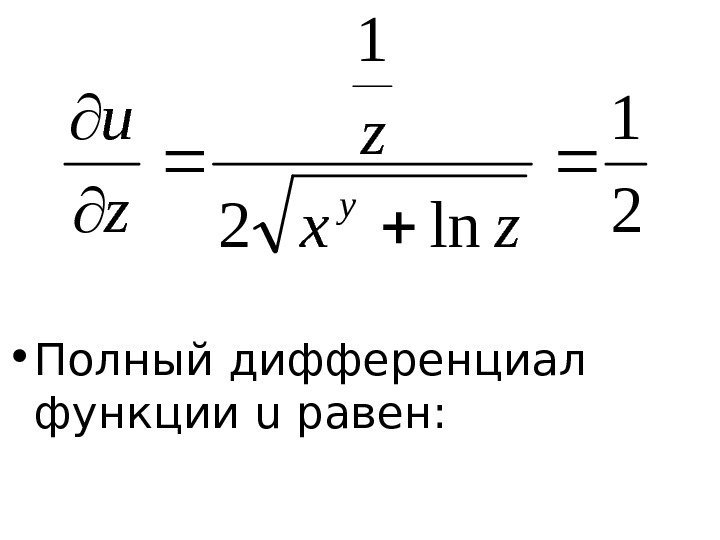 • Полный дифференциал функции u равен: 2 1 ln 2 1 zx z z u y
• Полный дифференциал функции u равен: 2 1 ln 2 1 zx z z u y
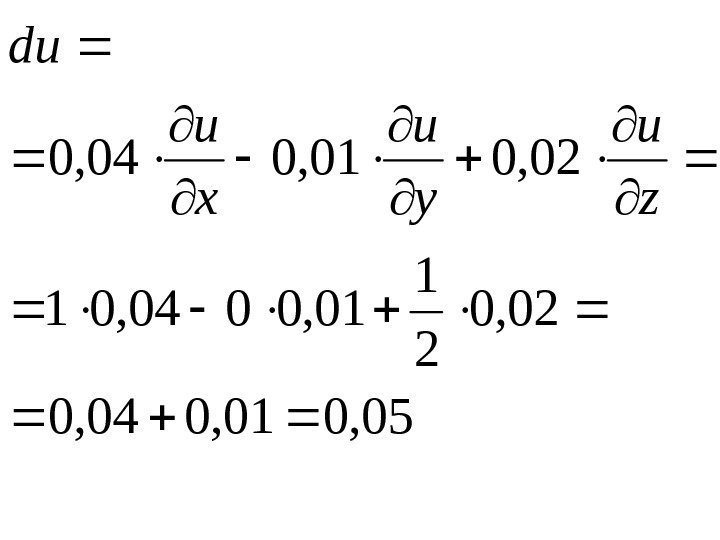 05, 001, 004, 0 02, 0 21 01, 0004, 01 02, 001, 004, 0 zu yu xudu
05, 001, 004, 0 02, 0 21 01, 0004, 01 02, 001, 004, 0 zu yu xudu
 • Точное значение этого выражения: 1, 049275225687319176. 05, 105, 01 )1, 2, 1( 02, 1 ln 04, 1 99, 1 duu
• Точное значение этого выражения: 1, 049275225687319176. 05, 105, 01 )1, 2, 1( 02, 1 ln 04, 1 99, 1 duu
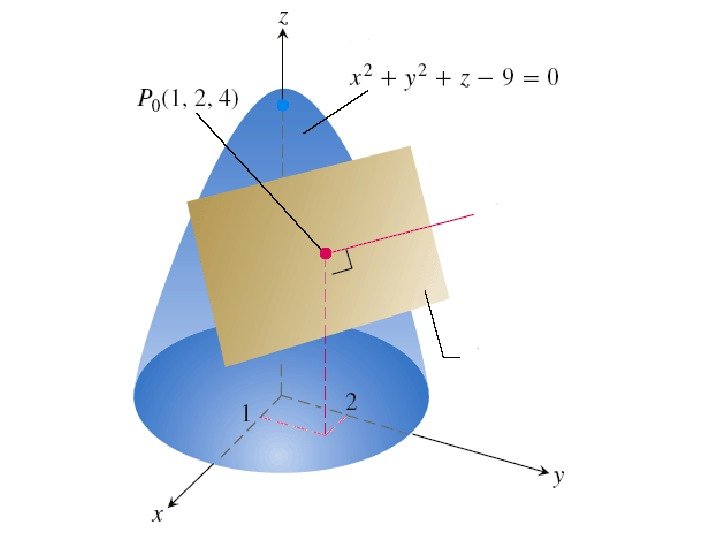
 § 6. Касательная плоскость и нормаль к поверхности
§ 6. Касательная плоскость и нормаль к поверхности
 • Касательной плоскостью к поверхности в ее точке M 0 называется плоскость, которая содержит все касательные к кривым, проведенным на поверхности через эту точку.
• Касательной плоскостью к поверхности в ее точке M 0 называется плоскость, которая содержит все касательные к кривым, проведенным на поверхности через эту точку.
 • Нормалью к поверхности в точке M 0 называется прямая, проходящая через эту точку и перпендикулярная касательной плоскости, проведенной в данной точке.
• Нормалью к поверхности в точке M 0 называется прямая, проходящая через эту точку и перпендикулярная касательной плоскости, проведенной в данной точке.

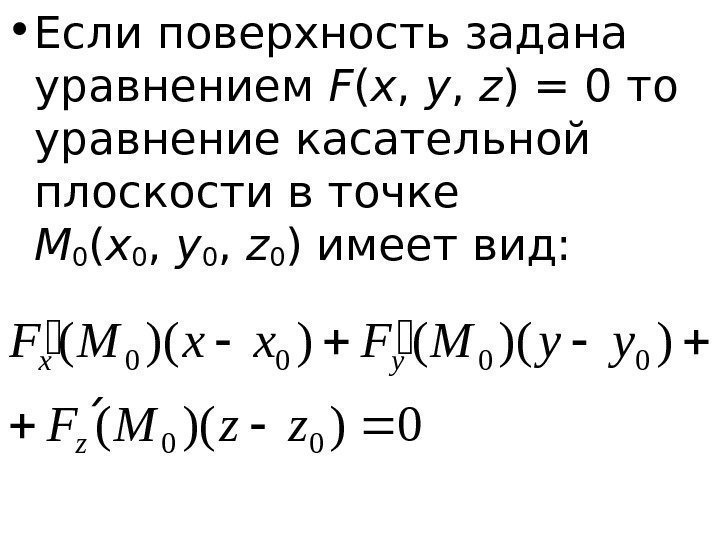 • Если поверхность задана уравнением F ( x , y , z ) = 0 то уравнение касательной плоскости в точке M 0 ( x 0 , y 0 , z 0 ) имеет вид: 0))(( 00 0000 zz. MF yy. MFxx. MF z yx
• Если поверхность задана уравнением F ( x , y , z ) = 0 то уравнение касательной плоскости в точке M 0 ( x 0 , y 0 , z 0 ) имеет вид: 0))(( 00 0000 zz. MF yy. MFxx. MF z yx
 • Уравнения нормали, проведенной к поверхности в точке M 0 ( x 0 , y 0 , z 0 ) , запишутся следующим образом: )()()( 0 0 0 MF zz MF yy MF xx zyx
• Уравнения нормали, проведенной к поверхности в точке M 0 ( x 0 , y 0 , z 0 ) , запишутся следующим образом: )()()( 0 0 0 MF zz MF yy MF xx zyx
 • Если поверхность задана уравнением z = f ( x , y ) , то уравнение касательной плоскости в точке M 0 ( x 0 , y 0 , z 0 ) имеет вид: ))(, (000 0000 yyyxf xxyxfzz y x
• Если поверхность задана уравнением z = f ( x , y ) , то уравнение касательной плоскости в точке M 0 ( x 0 , y 0 , z 0 ) имеет вид: ))(, (000 0000 yyyxf xxyxfzz y x
 • а уравнения нормали запишутся так: 1), ( 0 00 0 zz yxf yy yxf xx yx
• а уравнения нормали запишутся так: 1), ( 0 00 0 zz yxf yy yxf xx yx
 • Пример. Составить уравнения касательной плоскости и нормали к поверхности в точке M 0 ( x 0 , y 0 , z 0 ) , если 01332 22 yzxzxyyx. 1, 2 00 yx
• Пример. Составить уравнения касательной плоскости и нормали к поверхности в точке M 0 ( x 0 , y 0 , z 0 ) , если 01332 22 yzxzxyyx. 1, 2 00 yx
 • Решение. Подставляя x 0 и y 0 в уравнение поверхности, находим значение z 0 : откуда находим z 0 = 1. Следовательно, M 0 (2, – 1, 1) – точка касания. 01)1(32)1(23)1(2400 2 zz
• Решение. Подставляя x 0 и y 0 в уравнение поверхности, находим значение z 0 : откуда находим z 0 = 1. Следовательно, M 0 (2, – 1, 1) – точка касания. 01)1(32)1(23)1(2400 2 zz
 • По условию задачи поверхность задана неявно. Обозначим и найдем частные производные в точке M 0 (2, – 1, 1) : 1332), , ( 22 yzxzxyyxzyx.
• По условию задачи поверхность задана неявно. Обозначим и найдем частные производные в точке M 0 (2, – 1, 1) : 1332), , ( 22 yzxzxyyxzyx.
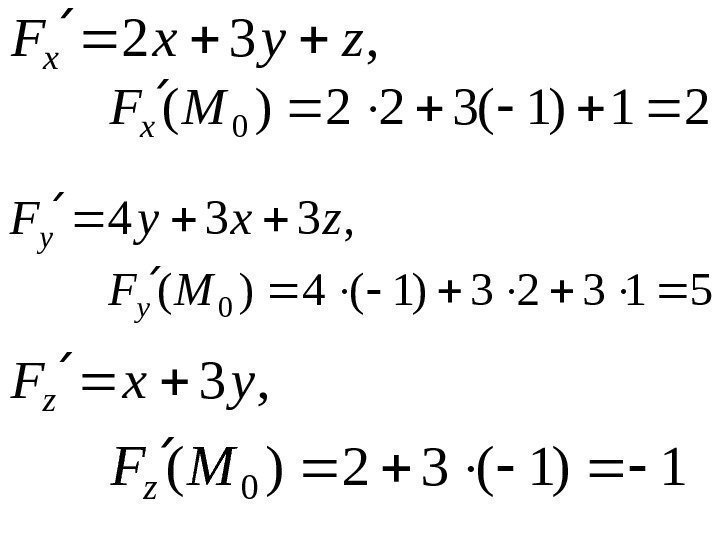 , 32 zyx. F x 21)1(322)( 0 MF x , 334 zxy. F y 51323)1(4)( 0 MF y , 3 yx. F z 1)1(32)( 0 MF z
, 32 zyx. F x 21)1(322)( 0 MF x , 334 zxy. F y 51323)1(4)( 0 MF y , 3 yx. F z 1)1(32)( 0 MF z
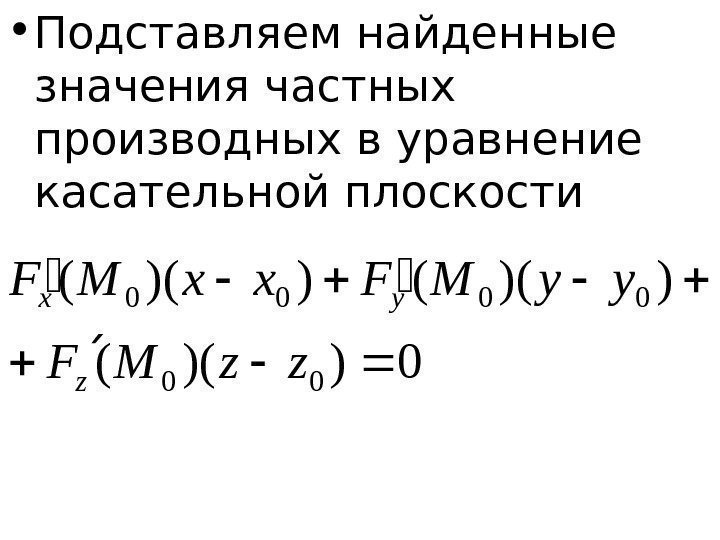 • Подставля ем найденные значения частных производных в уравнение касательной плоскости 0))(( 00 0000 zz. MF yy. MFxx. MF z yx
• Подставля ем найденные значения частных производных в уравнение касательной плоскости 0))(( 00 0000 zz. MF yy. MFxx. MF z yx
 и получаем искомое уравнение касательной плоскости: 0252 0)1(1)1(5)2(2 zyx
и получаем искомое уравнение касательной плоскости: 0252 0)1(1)1(5)2(2 zyx
 • У равнения нормали име ю т вид 1 1 5 1 2 2 zyx
• У равнения нормали име ю т вид 1 1 5 1 2 2 zyx
 § 7. Экстремум функции двух переменных
§ 7. Экстремум функции двух переменных
 • Определение. Функция z = f ( x , y ) имеет максимум в точке M 0 ( x 0 , y 0 ) , если существует такая окрестность этой точки, что для любых точек M ( x , y ) из этой окрестности выполняется неравенство ), ( 00 yxfyxf
• Определение. Функция z = f ( x , y ) имеет максимум в точке M 0 ( x 0 , y 0 ) , если существует такая окрестность этой точки, что для любых точек M ( x , y ) из этой окрестности выполняется неравенство ), ( 00 yxfyxf

 • Определение. Функция z = f ( x , y ) имеет минимум в точке M 0 ( x 0 , y 0 ) , если существует такая окрестность этой точки, что для любых точек M ( x , y ) из этой окрестности выполняется неравенство ), ( 00 yxfyxf
• Определение. Функция z = f ( x , y ) имеет минимум в точке M 0 ( x 0 , y 0 ) , если существует такая окрестность этой точки, что для любых точек M ( x , y ) из этой окрестности выполняется неравенство ), ( 00 yxfyxf

 • Точки максимума и минимума называют точками экстремума , а значения функции в этих точках называются экстремальными.
• Точки максимума и минимума называют точками экстремума , а значения функции в этих точках называются экстремальными.

 • Теорема 1 (необходимые условия экстремума). Если дифференцируемая функция z = f ( x , y ) имеет экстремум в точке M 0 ( x 0 , y 0 ) , то ее частные производные в этой точке равны нулю, т. е. 0 0 M x z 0 0 M y z
• Теорема 1 (необходимые условия экстремума). Если дифференцируемая функция z = f ( x , y ) имеет экстремум в точке M 0 ( x 0 , y 0 ) , то ее частные производные в этой точке равны нулю, т. е. 0 0 M x z 0 0 M y z
 • Функция z = f ( x , y ) может иметь экстремум и в точках, где функция непрерывна, но частные производные не существуют. • Точки, в которых и , называются стационарными точками функции z = f ( x , y ). 0 x z 0 y z
• Функция z = f ( x , y ) может иметь экстремум и в точках, где функция непрерывна, но частные производные не существуют. • Точки, в которых и , называются стационарными точками функции z = f ( x , y ). 0 x z 0 y z
 • Теорема 2 (достаточные условия экстремума). Пусть M 0 ( x 0 , y 0 ) является стационарной точкой функции z = f ( x , y ) и в ее окрестности существуют непрерывные частные производные 2 -го порядка.
• Теорема 2 (достаточные условия экстремума). Пусть M 0 ( x 0 , y 0 ) является стационарной точкой функции z = f ( x , y ) и в ее окрестности существуют непрерывные частные производные 2 -го порядка.
 • Обозначим и составим определитель Тогда: A x z M 0 2 2 B yx z M 02 C y z M
• Обозначим и составим определитель Тогда: A x z M 0 2 2 B yx z M 02 C y z M
 • 1) если Δ 0 , то в точке M 0 есть экстремум, причем максимум при A 0 ; • 3) если Δ = 0 , то требуется дополнительное исследование.
• 1) если Δ 0 , то в точке M 0 есть экстремум, причем максимум при A 0 ; • 3) если Δ = 0 , то требуется дополнительное исследование.



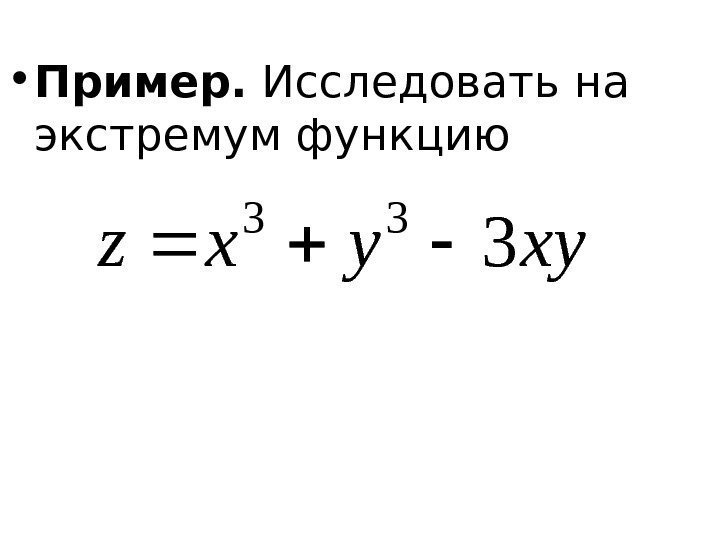 • Пример. Исследовать на экстремум функцию xyyxz
• Пример. Исследовать на экстремум функцию xyyxz
 • Решение. Находим частные производные 1 -го порядка yx x z 33 2 . 33 2 xy y z
• Решение. Находим частные производные 1 -го порядка yx x z 33 2 . 33 2 xy y z
 • Стационарные точки найдем из системы уравнений , 0 , 0 , 033 4 2 2 2 xx xy xy yx
• Стационарные точки найдем из системы уравнений , 0 , 0 , 033 4 2 2 2 xx xy xy yx
 • Получили две стационарные точки: M 1 (0, 0) , и M 2 (1, 1). . 1, 0, 1, 0 0)1(2121 3 yyxx xx
• Получили две стационарные точки: M 1 (0, 0) , и M 2 (1, 1). . 1, 0, 1, 0 0)1(2121 3 yyxx xx
 • Находим частные производные 2 -го порядка: • Исследуем каждую стационарную точку. y y z yx z x x z 6, 3,
• Находим частные производные 2 -го порядка: • Исследуем каждую стационарную точку. y y z yx z x x z 6, 3,
 • В точке M 1 (0, 0) имеем: A = 0 , B = – 3 , C = 0. • Тогда • Так как Δ < 0 , то в этой точке нет экстремума.
• В точке M 1 (0, 0) имеем: A = 0 , B = – 3 , C = 0. • Тогда • Так как Δ < 0 , то в этой точке нет экстремума.
 • В точке M 2 (1, 1) имеем: A = 6 , B = – 3 , C = 6. • В этом случае • Так как Δ >0 и A > 0 , то в этой точке функция имеет минимум 027936 1311)1; 1( min zz
• В точке M 2 (1, 1) имеем: A = 6 , B = – 3 , C = 6. • В этом случае • Так как Δ >0 и A > 0 , то в этой точке функция имеет минимум 027936 1311)1; 1( min zz


