Пример исследования Однофакторная линейная регрессионная модель

Пример исследования «Однофакторная линейная регрессионная модель»

• Цель работы: проверка умения решать основные типы задач по парному регрессионному анализу.

• Типы задач : 1. оценка с помощью МНК параметров линейного регрессионного уравнения; 2. экономическая интерпретация оценок параметров; 3. система нормальных уравнений и ее решение; 4. дисперсионный анализ; 5. нахождение коэффициента детерминации; 6. построение доверительных интервалов оценок параметров; 7. проверка гипотез о значимости оценок параметров; 8. проверка адекватности регрессии; 9. построение точечного прогноза по построенному линейному однофакторному уравнению регрессии; 10. построение доверительных интервалов для прогнозных значений

• Сначала следует определить причинную зависимость результативного признака (его вариации) от вариации факторного признак, т. е. определить, какой из данных показателей является фактором, а какой результатом. • Например. Расходы на питание — это переменная Y (результат), а душевой доход — переменная X (независимая переменная – фактор).

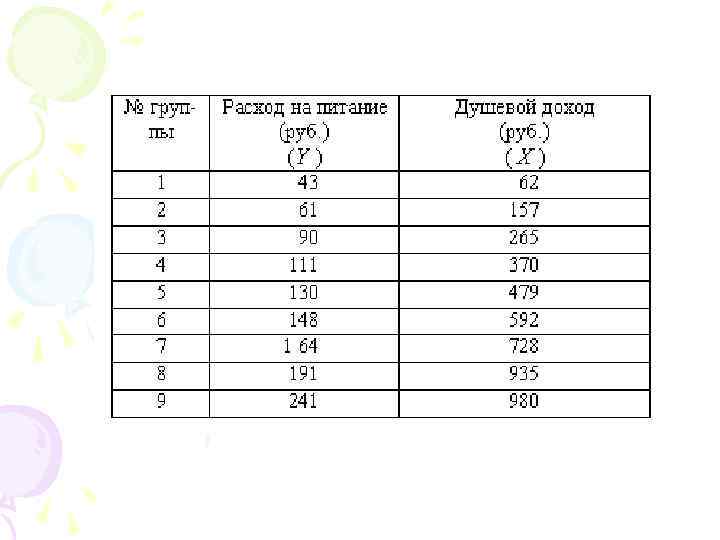
• Постройте поле корреляции и сделайте выводы о направлении и характере связи, выявите форму воздействия фактора X на результат Y.

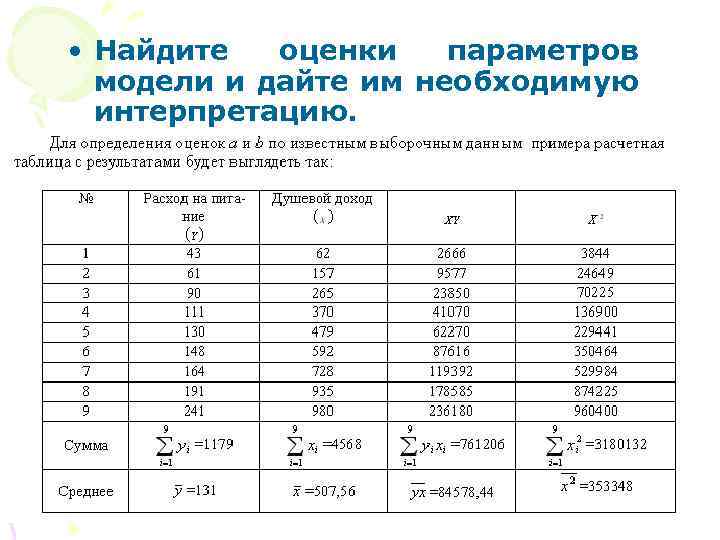• Найдите оценки параметров модели и дайте им необходимую интерпретацию.

• Коэффициентам уравнения линейной регрессии можно придать экономический смысл. • a) Коэффициент b=0, 19 показывает среднее изменение результативного показателя y с повышением или понижением величины фактора х на единицу его измерения. • В данном примере с увеличением дохода на 1 единицу расходы на питание повышаются в среднем на 0, 19. • Другими словами, из каждого дополнительного рубля дохода в среднем 0, 19 копеек будут израсходованы на питание.

• Связь между у и х определяет знак коэффициента регрессии b (если >0 – прямая связь, иначе обратная). • В нашем примере связь прямая, т. е. с увеличением душевого дохода расходы на питание также увеличиваются

• Коэффициент a=35, 1 формально показывает прогнозируемый уровень у, но только в том случае, если х =0 находится близко с выборочными значениями. • Но если х =0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.

• Подставив в уравнение регрессии соответствующие значения х, можно определить предсказанные значения результативного показателя для каждого наблюдения. • Полученные величины показывают, какой бы был расход на питание при соответствующих доходах, если бы данная группа n использовала бы свои доходы в такой степени, как в среднем все анализируемые группы

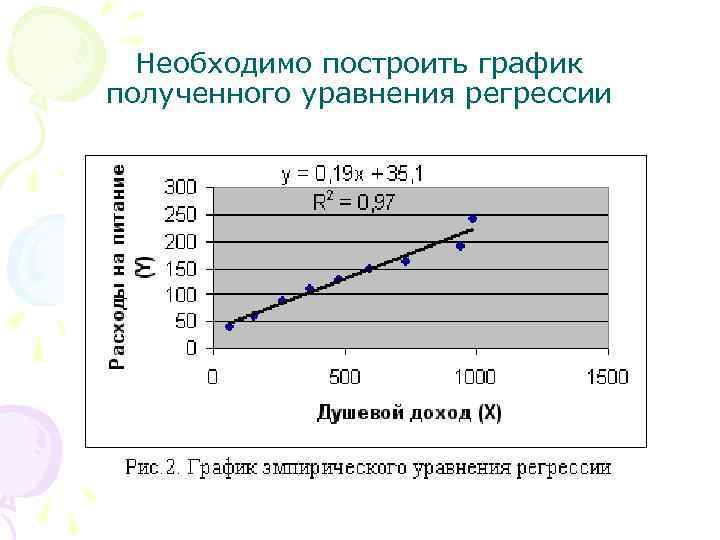Необходимо построить график полученного уравнения регрессии

• Далее нужно рассчитать показатель тесноты связи. • Таким показателем является выборочный линейный коэффициент корреляции r=0, 98. Таким образом, линейная связь между расходами на питание и душевым доходом очень тесная

• Определите коэффициент детерминации и дайте его интерпретацию • В нашем примере R 2=0, 97. • Это означает, что фактором душевого дохода можно объяснить почти 97% изменения расходов на питание. • Остальные 3% изменения расходов на питание объясняются факторами, не учтенными в модели

• Коэффициент эластичности равен что говорит о том, что если фактор x изменится на 1%, то фактор y изменится в среднем на 0, 58%.

• Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных

• Т. е. увеличение душевого дохода на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения расходов на питание на 0, 99 среднеквадратичного отклонения этих расходов. • Это означает, что при увеличении дохода в нашем примере на 309, 41 руб. , расходы на питание в среднем увеличатся на 58, 86 руб. (0, 99∙ 59, 45).

• «Проверка статистических гипотез» . • Для парной линейной регрессии оценка статистической значимости коэффициента β производится по следующему алгоритму: 1. Выдвигается нулевая гипотеза о том, что коэффициент регрессии статистически незначим: H 0: β =0 на уровне значимости α.

2. Определяется фактическое значение t-критерия для коэффициента регрессии по формуле где S(b) – стандартная ошибка для b

3. Определяется табличное значение tтабл. по таблицам распределения Стьюдента для заданного уровня значимости , принимая во внимание, что число степеней свободы для распределения Стьюдента равно (n-2).

3. Если фактическое значение t-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. • В противном случае говорят, что нулевая гипотеза отклоняется и на уровне значимости α принимается альтернативная гипотеза о статистической значимости коэффициента уравнения.

• В рассматриваемом примере S(b)= 0, 013, tфакт> tкрит, где tфакт = 14, 36 и tкрит. =2, 36. • Значит, коэффициент существенно отличен от нуля, и зависимость является достоверной

• Проверка значимости линейного коэффициента корреляции r проводится с помощью t-критерия Стьюдента: сравнивается с критическим значением t-критерия из таблицы значений с учетом заданного уровня значимости ( =0, 05) и числа степеней свободы (n-2). Если tнабл> tкритич. , то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). Т. е. делается вывод, что есть статистическая взаимосвязь.

• В парной регрессии, t 2 r = t 2 b , и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии. • В рассматриваемом примере t 2 r = t 2 b = 206, 20.

• • • Проверка значимости модели регрессии проводится с использованием Fкритерия Фишера, Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H 0: R 2=0 на уровне значимости α. Далее определяют фактическое значение F-критерия по формуле

• Если фактическое значение Fкритерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. • В противном случае, нулевая гипотеза отклоняется и с вероятностью (1 - ) принимается альтернативная гипотеза о статистической значимости уравнения в целом.

• В рассматриваемом примере а Fтабл. =5, 59. Таким образом, Fфакт. > Fтабл. , и принимается гипотеза о статистической значимости уравнения в целом.

• Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных. • Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.

• Эти значения могут быть получены на основе экстраполяционных методов, например с использованием средних абсолютных приростов факторных признаков; они могут быть получены также методами экспертных оценок или непосредственно заданы исследователем экономического процесса. • Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя

С доверительной вероятностью 0, 95 постройте доверительный интервал ожидаемого значения результативного признака, если факторный признак увеличится на 5% от своего среднего значения.

• Построим точечный прогноз y при хпрогн. = 1, 05 *xср=1, 05* 507, 56 = 532, 94(руб. ). • Для этого подставим в оценочное уравнение регрессии соответствующее значение хпрогн. . • Тогда прогнозное значение расходов на питание при прогнозном значении дохода, равном 532, 94 рубля, в среднем составит

• Точечный прогноз дополним расчетом стандартной ошибки sey и интервальной оценкой прогнозного значения y :