Семинар_5_РА(искл+включ+мультик).ppt
- Количество слайдов: 32
 Пример 5
Пример 5
 Пример По данным 20 сельскохозяйственных районов требуется построить регрессионную модель урожайности зерновых культур (у). Для анализа использовать следующие показатели: х1 -число колесных тракторов; х2 -число зерноуборочных комбайнов; х3 -число орудий поверхностной обработки почвы; х4 -количество удобрений; х5 -количество хим. удобрений.
Пример По данным 20 сельскохозяйственных районов требуется построить регрессионную модель урожайности зерновых культур (у). Для анализа использовать следующие показатели: х1 -число колесных тракторов; х2 -число зерноуборочных комбайнов; х3 -число орудий поверхностной обработки почвы; х4 -количество удобрений; х5 -количество хим. удобрений.
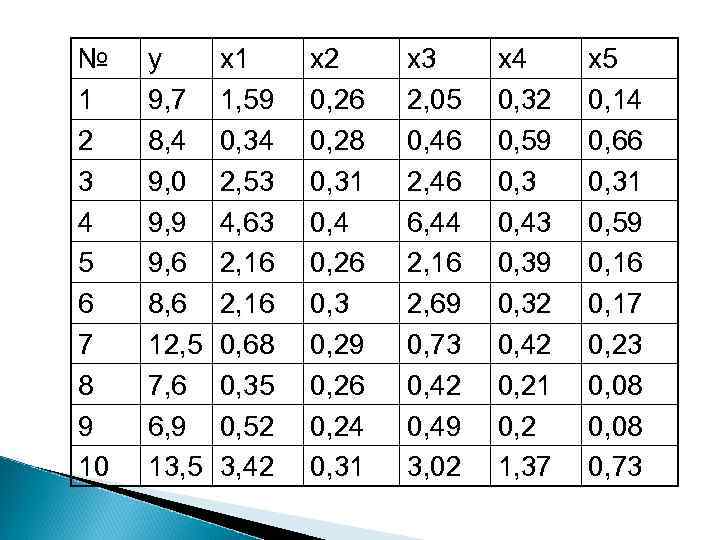 № 1 2 3 4 5 6 7 8 9 10 y 9, 7 8, 4 9, 0 9, 9 9, 6 8, 6 12, 5 7, 6 6, 9 13, 5 х1 1, 59 0, 34 2, 53 4, 63 2, 16 0, 68 0, 35 0, 52 3, 42 х2 0, 26 0, 28 0, 31 0, 4 0, 26 0, 3 0, 29 0, 26 0, 24 0, 31 х3 2, 05 0, 46 2, 46 6, 44 2, 16 2, 69 0, 73 0, 42 0, 49 3, 02 х4 0, 32 0, 59 0, 3 0, 43 0, 39 0, 32 0, 42 0, 21 0, 2 1, 37 х5 0, 14 0, 66 0, 31 0, 59 0, 16 0, 17 0, 23 0, 08 0, 73
№ 1 2 3 4 5 6 7 8 9 10 y 9, 7 8, 4 9, 0 9, 9 9, 6 8, 6 12, 5 7, 6 6, 9 13, 5 х1 1, 59 0, 34 2, 53 4, 63 2, 16 0, 68 0, 35 0, 52 3, 42 х2 0, 26 0, 28 0, 31 0, 4 0, 26 0, 3 0, 29 0, 26 0, 24 0, 31 х3 2, 05 0, 46 2, 46 6, 44 2, 16 2, 69 0, 73 0, 42 0, 49 3, 02 х4 0, 32 0, 59 0, 3 0, 43 0, 39 0, 32 0, 42 0, 21 0, 2 1, 37 х5 0, 14 0, 66 0, 31 0, 59 0, 16 0, 17 0, 23 0, 08 0, 73
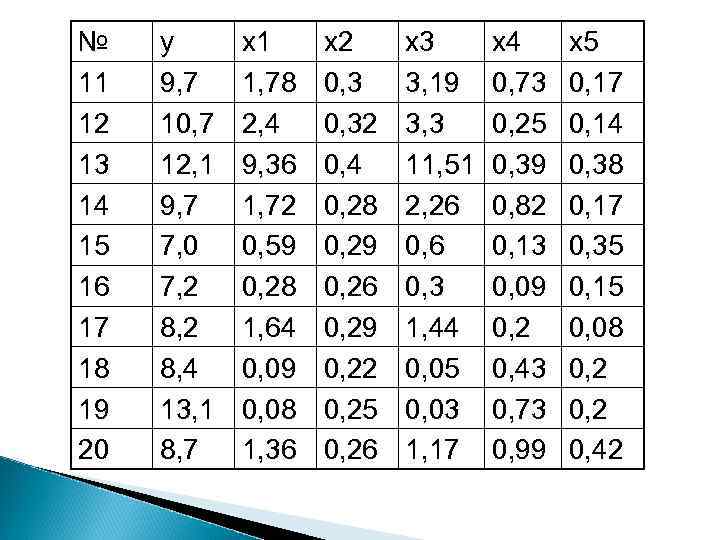 № 11 12 13 14 15 16 17 18 19 20 y 9, 7 10, 7 12, 1 9, 7 7, 0 7, 2 8, 4 13, 1 8, 7 х1 1, 78 2, 4 9, 36 1, 72 0, 59 0, 28 1, 64 0, 09 0, 08 1, 36 х2 0, 32 0, 4 0, 28 0, 29 0, 26 0, 29 0, 22 0, 25 0, 26 х3 3, 19 3, 3 11, 51 2, 26 0, 3 1, 44 0, 05 0, 03 1, 17 х4 0, 73 0, 25 0, 39 0, 82 0, 13 0, 09 0, 2 0, 43 0, 73 0, 99 х5 0, 17 0, 14 0, 38 0, 17 0, 35 0, 15 0, 08 0, 2 0, 42
№ 11 12 13 14 15 16 17 18 19 20 y 9, 7 10, 7 12, 1 9, 7 7, 0 7, 2 8, 4 13, 1 8, 7 х1 1, 78 2, 4 9, 36 1, 72 0, 59 0, 28 1, 64 0, 09 0, 08 1, 36 х2 0, 32 0, 4 0, 28 0, 29 0, 26 0, 29 0, 22 0, 25 0, 26 х3 3, 19 3, 3 11, 51 2, 26 0, 3 1, 44 0, 05 0, 03 1, 17 х4 0, 73 0, 25 0, 39 0, 82 0, 13 0, 09 0, 2 0, 43 0, 73 0, 99 х5 0, 17 0, 14 0, 38 0, 17 0, 35 0, 15 0, 08 0, 2 0, 42
 Решение. Построим Получим уравнение регрессии в виде: оценку уравнения: Уравнения регрессии значимо, т. к. Fнабл > Fкр Fнабл Fкр(α=0, 1; ν 1=5; ν 2=14)=2, 31.
Решение. Построим Получим уравнение регрессии в виде: оценку уравнения: Уравнения регрессии значимо, т. к. Fнабл > Fкр Fнабл Fкр(α=0, 1; ν 1=5; ν 2=14)=2, 31.
 Решение. Приступаем к проверке значимости отдельных коэффициентов регрессии - H 0: j=0: tкр(α; ν=n-k-1)
Решение. Приступаем к проверке значимости отдельных коэффициентов регрессии - H 0: j=0: tкр(α; ν=n-k-1)
 Решение. Приступаем у проверке значимости отдельных коэффициентов регрессии - H 0: j=0: tкр(α; ν=n-k-1) Получим оценку уравнения: В скобках – расчетные значения t-критерия для проверки значимости коэффициентов регрессии.
Решение. Приступаем у проверке значимости отдельных коэффициентов регрессии - H 0: j=0: tкр(α; ν=n-k-1) Получим оценку уравнения: В скобках – расчетные значения t-критерия для проверки значимости коэффициентов регрессии.
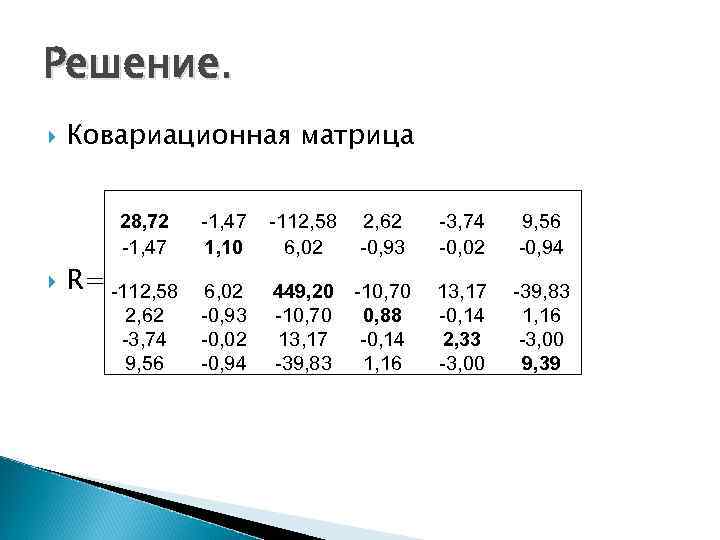 Решение. Ковариационная матрица 28, 72 -1, 47 R= -112, 58 2, 62 -3, 74 9, 56 -1, 47 1, 10 -112, 58 6, 02 2, 62 -0, 93 -3, 74 -0, 02 9, 56 -0, 94 6, 02 -0, 93 -0, 02 -0, 94 449, 20 -10, 70 13, 17 -39, 83 -10, 70 0, 88 -0, 14 1, 16 13, 17 -0, 14 2, 33 -3, 00 -39, 83 1, 16 -3, 00 9, 39
Решение. Ковариационная матрица 28, 72 -1, 47 R= -112, 58 2, 62 -3, 74 9, 56 -1, 47 1, 10 -112, 58 6, 02 2, 62 -0, 93 -3, 74 -0, 02 9, 56 -0, 94 6, 02 -0, 93 -0, 02 -0, 94 449, 20 -10, 70 13, 17 -39, 83 -10, 70 0, 88 -0, 14 1, 16 13, 17 -0, 14 2, 33 -3, 00 -39, 83 1, 16 -3, 00 9, 39
 Решение. Проверка значимости отдельных коэффициентов регрессии дает, что значимым является b 4, т. к. tкр(α=0, 1; ν=14)=1, 761. Экономически не интерпретируются отрицательные знаки коэффициентов регрессии при х3 и х5.
Решение. Проверка значимости отдельных коэффициентов регрессии дает, что значимым является b 4, т. к. tкр(α=0, 1; ν=14)=1, 761. Экономически не интерпретируются отрицательные знаки коэффициентов регрессии при х3 и х5.
 Пошаговый алгоритм исключения переменных Исключим из модели переменную х3, т. к. ей соответствует минимальное по абсолютной величине значение tстатистики (-0, 66). Для оставшихся переменных строим уравнение регрессии:
Пошаговый алгоритм исключения переменных Исключим из модели переменную х3, т. к. ей соответствует минимальное по абсолютной величине значение tстатистики (-0, 66). Для оставшихся переменных строим уравнение регрессии:
 Решение. Уравнения регрессии значимо, т. к. Fнабл=4, 009 > Fкр(α=0, 1; ν 1=4; ν 2=15)=2, 36. Проверка значимости отдельных коэффициентов регрессии дает, что значимым является b 4, т. к. tкр(α=0, 1; ν=15)=1, 75. Экономически не интерпретируются отрицательный знак коэффициента регрессии при х5.
Решение. Уравнения регрессии значимо, т. к. Fнабл=4, 009 > Fкр(α=0, 1; ν 1=4; ν 2=15)=2, 36. Проверка значимости отдельных коэффициентов регрессии дает, что значимым является b 4, т. к. tкр(α=0, 1; ν=15)=1, 75. Экономически не интерпретируются отрицательный знак коэффициента регрессии при х5.
 Пошаговый алгоритм исключения переменных Исключим из модели переменную х1, т. к. ей соответствует минимальное по абсолютной величине значение t-статистики (0, 32). Для оставшихся переменных строим уравнение регрессии:
Пошаговый алгоритм исключения переменных Исключим из модели переменную х1, т. к. ей соответствует минимальное по абсолютной величине значение t-статистики (0, 32). Для оставшихся переменных строим уравнение регрессии:
 Решение. Уравнения регрессии значимо, т. к. Fнабл=5, 628 > Fкр(α=0, 1; ν 1=3; ν 2=16)=2, 46. Проверка значимости отдельных коэффициентов регрессии дает, что значимым является b 2 и b 4, т. к. tкр(α=0, 1; ν=16)=1, 746. Экономически не интерпретируются отрицательный знак коэффициента регрессии при х5.
Решение. Уравнения регрессии значимо, т. к. Fнабл=5, 628 > Fкр(α=0, 1; ν 1=3; ν 2=16)=2, 46. Проверка значимости отдельных коэффициентов регрессии дает, что значимым является b 2 и b 4, т. к. tкр(α=0, 1; ν=16)=1, 746. Экономически не интерпретируются отрицательный знак коэффициента регрессии при х5.
 Пошаговый алгоритм исключения переменных Исключим из модели переменную х5, т. к. ей соответствует минимальное по абсолютной величине значение t-статистики (1, 3). Для оставшихся переменных строим уравнение регрессии:
Пошаговый алгоритм исключения переменных Исключим из модели переменную х5, т. к. ей соответствует минимальное по абсолютной величине значение t-статистики (1, 3). Для оставшихся переменных строим уравнение регрессии:
 Решение. Уравнения регрессии значимо, т. к. Fнабл=7, 297 > Fкр(α=0, 1; ν 1=2; ν 2=17)=2, 64. Проверка значимости отдельных коэффициентов регрессии дает, что все значимы, т. к. tкр(α=0, 1; ν=17)=1, 739. Итак, получили уравнение регрессии:
Решение. Уравнения регрессии значимо, т. к. Fнабл=7, 297 > Fкр(α=0, 1; ν 1=2; ν 2=17)=2, 64. Проверка значимости отдельных коэффициентов регрессии дает, что все значимы, т. к. tкр(α=0, 1; ν=17)=1, 739. Итак, получили уравнение регрессии:
 Решение. Для получения уравнения регрессии мы использовали алгоритм пошагового исключения переменных. Помним, что его минусом является большая вероятность пропуска наилучшего состава регрессоров. Возникает вопрос: «Является ли оно самой лучшей моделью? »
Решение. Для получения уравнения регрессии мы использовали алгоритм пошагового исключения переменных. Помним, что его минусом является большая вероятность пропуска наилучшего состава регрессоров. Возникает вопрос: «Является ли оно самой лучшей моделью? »
 Решение. Абсолютно надежным методом поиска наилучшего состава регрессоров из имеющихся является перебор всех их возможных комбинаций. Однако этот способ предполагает необходимость построения и анализа большого числа моделей. Проверим наши регрессоры на наличие мультиколлинеарности.
Решение. Абсолютно надежным методом поиска наилучшего состава регрессоров из имеющихся является перебор всех их возможных комбинаций. Однако этот способ предполагает необходимость построения и анализа большого числа моделей. Проверим наши регрессоры на наличие мультиколлинеарности.
 Мультиколлинеарность Линейная зависимость между переменными Если парный коэффициент корреляции больше 0, 8.
Мультиколлинеарность Линейная зависимость между переменными Если парный коэффициент корреляции больше 0, 8.
 Решение. Построим и проанализируем матрицу парных коэффициентов корреляции:
Решение. Построим и проанализируем матрицу парных коэффициентов корреляции:
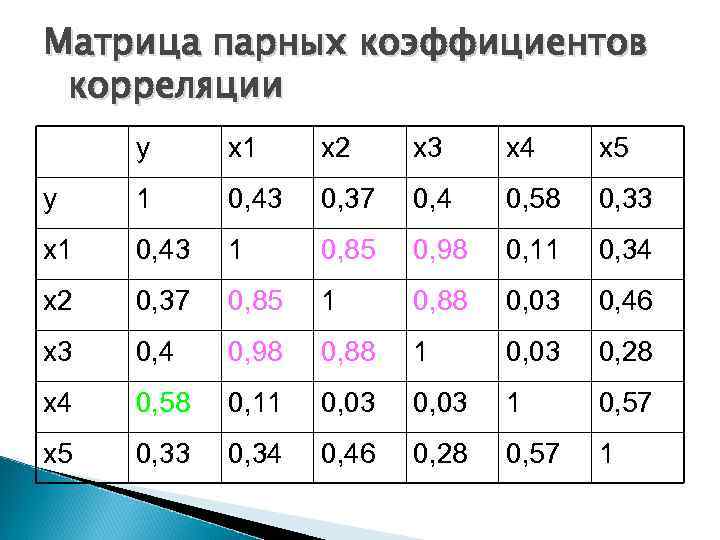 Матрица парных коэффициентов корреляции y х1 х2 х3 х4 х5 у 1 0, 43 0, 37 0, 4 0, 58 0, 33 х1 0, 43 1 0, 85 0, 98 0, 11 0, 34 х2 0, 37 0, 85 1 0, 88 0, 03 0, 46 х3 0, 4 0, 98 0, 88 1 0, 03 0, 28 х4 0, 58 0, 11 0, 03 1 0, 57 х5 0, 33 0, 34 0, 46 0, 28 0, 57 1
Матрица парных коэффициентов корреляции y х1 х2 х3 х4 х5 у 1 0, 43 0, 37 0, 4 0, 58 0, 33 х1 0, 43 1 0, 85 0, 98 0, 11 0, 34 х2 0, 37 0, 85 1 0, 88 0, 03 0, 46 х3 0, 4 0, 98 0, 88 1 0, 03 0, 28 х4 0, 58 0, 11 0, 03 1 0, 57 х5 0, 33 0, 34 0, 46 0, 28 0, 57 1
 Анализ матрицы 1. 2. Показывает, что результативный показатель (у) наиболее тесно связан с показателем х4 - количество удобрений (зеленый цвет): ryx 4=0, 58. О наличии мультиколлинеарности свидетельствуют (розовый): rx 1 x 3=0, 98 (почти функциональная зависимость) rх1 х2=0, 85 rx 3 x 2=0, 88.
Анализ матрицы 1. 2. Показывает, что результативный показатель (у) наиболее тесно связан с показателем х4 - количество удобрений (зеленый цвет): ryx 4=0, 58. О наличии мультиколлинеарности свидетельствуют (розовый): rx 1 x 3=0, 98 (почти функциональная зависимость) rх1 х2=0, 85 rx 3 x 2=0, 88.
 Анализ матрицы Так как анализ матрицы коэффициентов корреляции выявил наличие мультиколлинеарности, то для получения оптимального уравнения регрессии есть смысл использовать алгоритм пошагового включения переменных.
Анализ матрицы Так как анализ матрицы коэффициентов корреляции выявил наличие мультиколлинеарности, то для получения оптимального уравнения регрессии есть смысл использовать алгоритм пошагового включения переменных.
 Пошаговый алгоритм с включением переменных 1 шаг: в модель включим объясняющую переменную х4, имеющую самый высокий коэффициент корреляции с зависимой переменной Получим уравнение регрессии:
Пошаговый алгоритм с включением переменных 1 шаг: в модель включим объясняющую переменную х4, имеющую самый высокий коэффициент корреляции с зависимой переменной Получим уравнение регрессии:
 Пошаговый алгоритм с включением переменных 2 шаг: включаем поочередно остальные переменные х1, х2, х3 и х5, получаем:
Пошаговый алгоритм с включением переменных 2 шаг: включаем поочередно остальные переменные х1, х2, х3 и х5, получаем:
 Пошаговый алгоритм с включением переменных 2 шаг: включаем поочередно остальные переменные х1, х2, х3 и х5, получаем: Проверка значимости уравнений показывает, что все уравнения значимы: Fкр(0, 1; 2; 17)=2, 645 Fнабл(х1)=7, 52 Fнабл(х2)=7, 29 Fнабл(х3)=7, 42 Fнабл(х5)=4, 25
Пошаговый алгоритм с включением переменных 2 шаг: включаем поочередно остальные переменные х1, х2, х3 и х5, получаем: Проверка значимости уравнений показывает, что все уравнения значимы: Fкр(0, 1; 2; 17)=2, 645 Fнабл(х1)=7, 52 Fнабл(х2)=7, 29 Fнабл(х3)=7, 42 Fнабл(х5)=4, 25
 Пошаговый алгоритм с включением переменных Проверка значимости коэффициентов регрессии в каждом уравнении показывает значимость всех, кроме коэффициента при х5. Следовательно, исключаем уравнение регрессии, содержащее переменную х5.
Пошаговый алгоритм с включением переменных Проверка значимости коэффициентов регрессии в каждом уравнении показывает значимость всех, кроме коэффициента при х5. Следовательно, исключаем уравнение регрессии, содержащее переменную х5.
 Пошаговый алгоритм с включением переменных 3 шаг: включаем в отобранные три уравнения по очереди каждую из оставшихся переменных. Получаем уравнения регрессии:
Пошаговый алгоритм с включением переменных 3 шаг: включаем в отобранные три уравнения по очереди каждую из оставшихся переменных. Получаем уравнения регрессии:
 Пошаговый алгоритм с включением переменных Включение в эти уравнения дополнительно любой из трех оставшихся переменных приводит к тому, что уравнения регрессии в целом значимо, но появляются не значимые коэффициенты. Процедура включения завершена.
Пошаговый алгоритм с включением переменных Включение в эти уравнения дополнительно любой из трех оставшихся переменных приводит к тому, что уравнения регрессии в целом значимо, но появляются не значимые коэффициенты. Процедура включения завершена.
 Выбор лучшей модели Итак, методом исключения получили 1 модель и методом включения получили еще 2 модели. Какая является лучшей? Та, что имеет лучшую информативность (т. е. наибольший коэффициент детерминации) и ясный экономический смысл (логическая интерпретация).
Выбор лучшей модели Итак, методом исключения получили 1 модель и методом включения получили еще 2 модели. Какая является лучшей? Та, что имеет лучшую информативность (т. е. наибольший коэффициент детерминации) и ясный экономический смысл (логическая интерпретация).
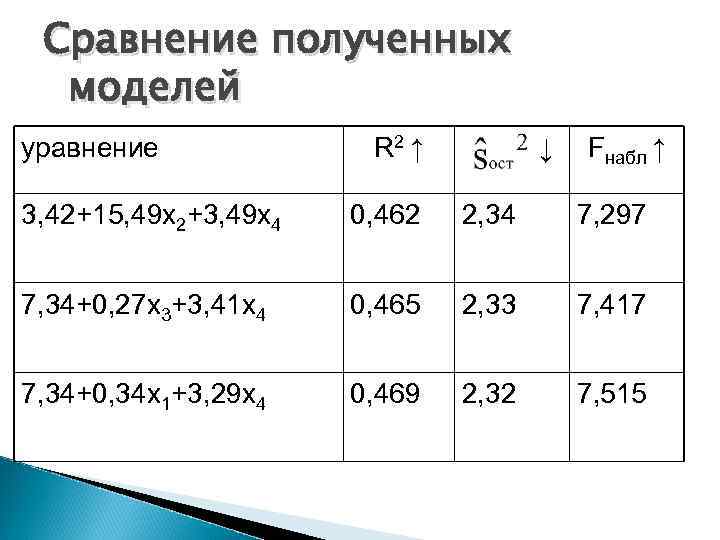 Сравнение полученных моделей уравнение R 2 ↑ ↓ Fнабл ↑ 3, 42+15, 49 х2+3, 49 х4 0, 462 2, 34 7, 297 7, 34+0, 27 х3+3, 41 х4 0, 465 2, 33 7, 417 7, 34+0, 34 х1+3, 29 х4 0, 469 2, 32 7, 515
Сравнение полученных моделей уравнение R 2 ↑ ↓ Fнабл ↑ 3, 42+15, 49 х2+3, 49 х4 0, 462 2, 34 7, 297 7, 34+0, 27 х3+3, 41 х4 0, 465 2, 33 7, 417 7, 34+0, 34 х1+3, 29 х4 0, 469 2, 32 7, 515
 Выбор лучшей модели По статистическим критериям наиболее адекватна последняя из моделей. Ей соответствует минимальное значение остаточной дисперсии, а также наибольшие значения коэффициента детерминации и Fстатистики. Несколько худшими показателями обладает вторая модель, затем следует модель (первая), полученная методом пошагового исключения переменных.
Выбор лучшей модели По статистическим критериям наиболее адекватна последняя из моделей. Ей соответствует минимальное значение остаточной дисперсии, а также наибольшие значения коэффициента детерминации и Fстатистики. Несколько худшими показателями обладает вторая модель, затем следует модель (первая), полученная методом пошагового исключения переменных.
 Интерпретация модели Множественный коэффициент детерминации свидетельствует о том, что только 46, 9% вариации урожайности объясняется вошедшими в модель факторами x 1 и x 4, то есть насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием не учтенных факторов (x 2, x 3, x 5, погодными условиями, особенностями почвы и другими).
Интерпретация модели Множественный коэффициент детерминации свидетельствует о том, что только 46, 9% вариации урожайности объясняется вошедшими в модель факторами x 1 и x 4, то есть насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием не учтенных факторов (x 2, x 3, x 5, погодными условиями, особенностями почвы и другими).


