 Пример 1 //Ищет элемент e в массиве a. //Возвращает индекс элемента //в массиве или -1, если элемент не найден static int find. Element(int e, int[] a) { for (int i = 0; i < a. Length; i++) if (a[i] == e) return i; return -1; }
Пример 1 //Ищет элемент e в массиве a. //Возвращает индекс элемента //в массиве или -1, если элемент не найден static int find. Element(int e, int[] a) { for (int i = 0; i < a. Length; i++) if (a[i] == e) return i; return -1; }
 Пример 2 //Ищет последовательность элементов e в массиве a. //Возвращает индекс первого элемента посл-ти //в массиве или -1, если элемент не найден static int find. Seq(int[] e, int[] a) { if (e. Length > a. Length) return -1; for (int i = 0; i
Пример 2 //Ищет последовательность элементов e в массиве a. //Возвращает индекс первого элемента посл-ти //в массиве или -1, если элемент не найден static int find. Seq(int[] e, int[] a) { if (e. Length > a. Length) return -1; for (int i = 0; i
 Бинарный поиск. Производительность бинарного поиска - log 2(n). При n = 1000 бинарный поиск в 100 раз быстрее последовательного, а при n = 1 000 в 50 000 раз.
Бинарный поиск. Производительность бинарного поиска - log 2(n). При n = 1000 бинарный поиск в 100 раз быстрее последовательного, а при n = 1 000 в 50 000 раз.
 Пример 3. //искать заданный элемент в массиве //если нашли - вернуть его индекс в массиве //если не нашли - вернуть -1 static int find. Binary(int e, int[] ar) { int a, b, c; if (e <= ar[0] || ar[ar. Length-1] < e) return -1; else
Пример 3. //искать заданный элемент в массиве //если нашли - вернуть его индекс в массиве //если не нашли - вернуть -1 static int find. Binary(int e, int[] ar) { int a, b, c; if (e <= ar[0] || ar[ar. Length-1] < e) return -1; else
 a = 0; b = ar. Length-1 ; while (a != (b - 1)) { c = (a + b) / 2; if (ar[c] < e) a = c; else if (ar[c] == e) {b = c; a = b - 1; } else if (ar[c] > e) b = c; } if (b <= ar. Length-1 && ar[b] == e) return b; else return -1; }
a = 0; b = ar. Length-1 ; while (a != (b - 1)) { c = (a + b) / 2; if (ar[c] < e) a = c; else if (ar[c] == e) {b = c; a = b - 1; } else if (ar[c] > e) b = c; } if (b <= ar. Length-1 && ar[b] == e) return b; else return -1; }
 Поиск. m-блочный поиск. Исходный массив B длины n делится на m упорядоченных подмассивов B 1, B 2, …, Bm. Они имеют длины n 1, n 2, …, nm, причем сумма этих длин равна n. При поиске v сначала определяется первый из подмассивов Bi, у которого последний элемент больше v, а потом к этому подмассиву применяется последовательный поиск.
Поиск. m-блочный поиск. Исходный массив B длины n делится на m упорядоченных подмассивов B 1, B 2, …, Bm. Они имеют длины n 1, n 2, …, nm, причем сумма этих длин равна n. При поиске v сначала определяется первый из подмассивов Bi, у которого последний элемент больше v, а потом к этому подмассиву применяется последовательный поиск.
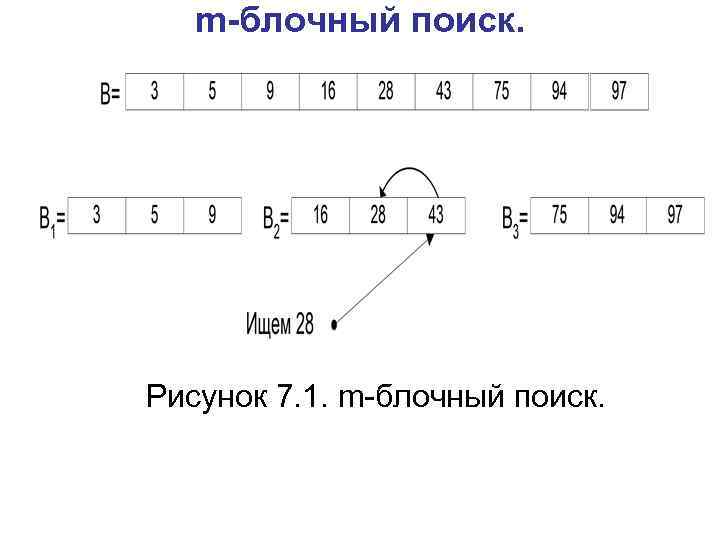 m-блочный поиск. Рисунок 7. 1. m-блочный поиск.
m-блочный поиск. Рисунок 7. 1. m-блочный поиск.
 m-блочный поиск. Если длины всех подсписков примерно одинаковы, , то максимальное быстродействие m-блочного поиска равняется . При одинаковой частоте использования всех элементов среднее быстродействие m-блочного поиска равняется .
m-блочный поиск. Если длины всех подсписков примерно одинаковы, , то максимальное быстродействие m-блочного поиска равняется . При одинаковой частоте использования всех элементов среднее быстродействие m-блочного поиска равняется .
 Задача выбора. В массиве целых чисел длины n, необходимо найти элемент, который разместился бы на i-ом месте, если массив упорядочить по убыванию. Это задача выбора i-го наибольшего значения. Сформулированная задача является симметричной в том смысле, что поиск i-го наибольшего значения эквивалентен поиску (n-i+1)-го наименьшего значения.
Задача выбора. В массиве целых чисел длины n, необходимо найти элемент, который разместился бы на i-ом месте, если массив упорядочить по убыванию. Это задача выбора i-го наибольшего значения. Сформулированная задача является симметричной в том смысле, что поиск i-го наибольшего значения эквивалентен поиску (n-i+1)-го наименьшего значения.
 Пример 4 //решает задачу выбора i-го элемента //в массиве a, если бы он был отсортирован //по убыванию //возвращает значение требуемого элемента static int find. I(int i, int [] a) { int x; for (int j = 0; j <= i; j++) for (int z = j + 1; z
Пример 4 //решает задачу выбора i-го элемента //в массиве a, если бы он был отсортирован //по убыванию //возвращает значение требуемого элемента static int find. I(int i, int [] a) { int x; for (int j = 0; j <= i; j++) for (int z = j + 1; z
 Алгоритм Бойера-Мура. Пусть у нас есть набор символов из пяти символов: a, b, c, d, e и мы хотим найти вхождение образца “abbad” например, в строке “abeccacbadbabbad”. Рисунок 7. 2. Таблица смещений для образца “abbad”.
Алгоритм Бойера-Мура. Пусть у нас есть набор символов из пяти символов: a, b, c, d, e и мы хотим найти вхождение образца “abbad” например, в строке “abeccacbadbabbad”. Рисунок 7. 2. Таблица смещений для образца “abbad”.
 Алгоритм Бойера-Мура. Рисунок 7. 3. Начало поиска.
Алгоритм Бойера-Мура. Рисунок 7. 3. Начало поиска.
 Алгоритм Бойера-Мура. Рисунок 7. 4. Продолжение поиска.
Алгоритм Бойера-Мура. Рисунок 7. 4. Продолжение поиска.
 Алгоритм Бойера-Мура. Рисунок 7. 5. Продолжение поиска.
Алгоритм Бойера-Мура. Рисунок 7. 5. Продолжение поиска.
 Алгоритм Бойера-Мура. Рисунок 7. 6. Продолжение поиска.
Алгоритм Бойера-Мура. Рисунок 7. 6. Продолжение поиска.
 Алгоритм Бойера-Мура. Рисунок 7. 7. Продолжение поиска.
Алгоритм Бойера-Мура. Рисунок 7. 7. Продолжение поиска.
 Алгоритм Бойера-Мура. Рисунок 7. 8. Окончание поиска.
Алгоритм Бойера-Мура. Рисунок 7. 8. Окончание поиска.