Применения двойного интеграла Пушникова Марина Юрьевна Замена

Применения двойного интеграла Пушникова Марина Юрьевна

Замена переменных в двойном интеграле Если x=x(u; v) и y=y(u; v), эти функции непрерывны вместе с частными производными первого порядка по u и v в некоторой замкнутой -называется якобианом области G плоскости Ouv и взаимно однозначно где преобразования отражают область G на область D, тогда G в D

Двойной интеграл в полярных координатах К полярным координатам удобно переходить в тех случаях, когда область интегрирования круг или часть круга

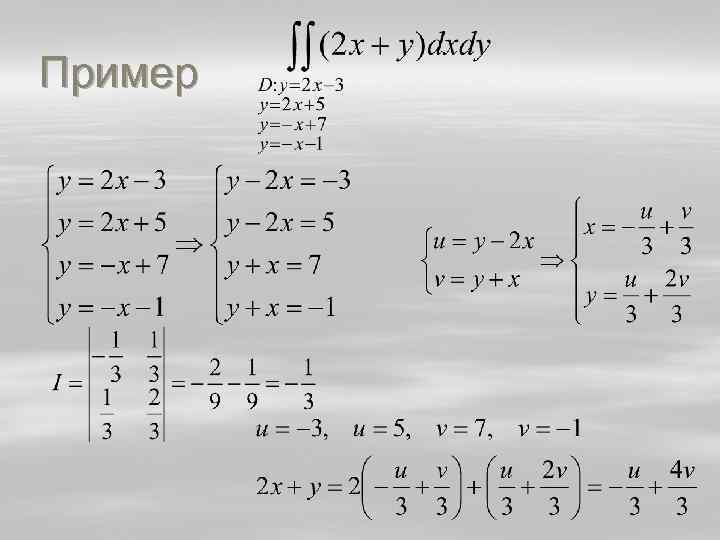Пример

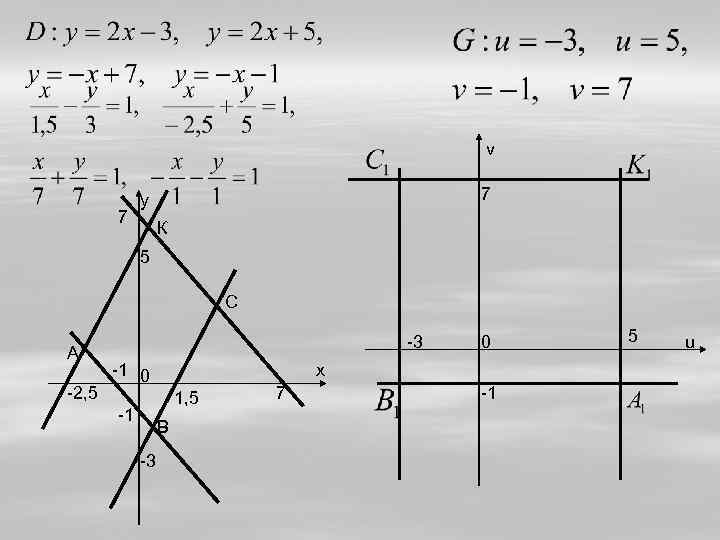v 7 7 у К 5 С А -2, 5 -3 -1 0 х 1, 5 -1 В -3 0 7 -1 5 u

Пример у р 0 х

Применения двойного интеграла § § При вычислении площади фигур При вычислении объемов тел При вычислении площади поверхности тел При вычислении массы материальной пластины по известной плотности § При вычислении моментов инерции материальной пластины по известной плотности § При вычислении координат центра тяжести материальной пластины по известной плотности

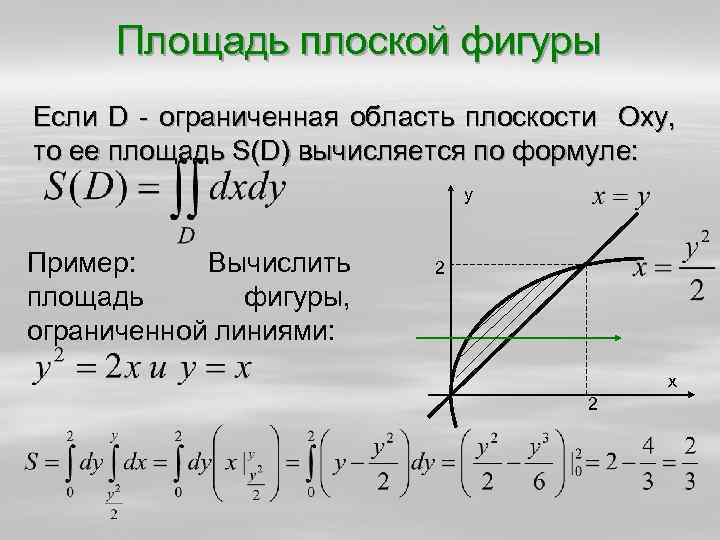Площадь плоской фигуры Если D - ограниченная область плоскости Oxy, то ее площадь S(D) вычисляется по формуле: у Пример: Вычислить площадь фигуры, ограниченной линиями: 2 х 2

Вычисление объема тела Если V - тело, ограниченное сверху поверхностью z=f(x; y) (неотрицательная и непрерывная функция в замкнутой области D), снизу – областью D, а сбоку – соответствующей цилиндрической поверхностью с образующей параллельной оси Oz и направляющей, совпадающей с границей области D, то объем этого тела равен

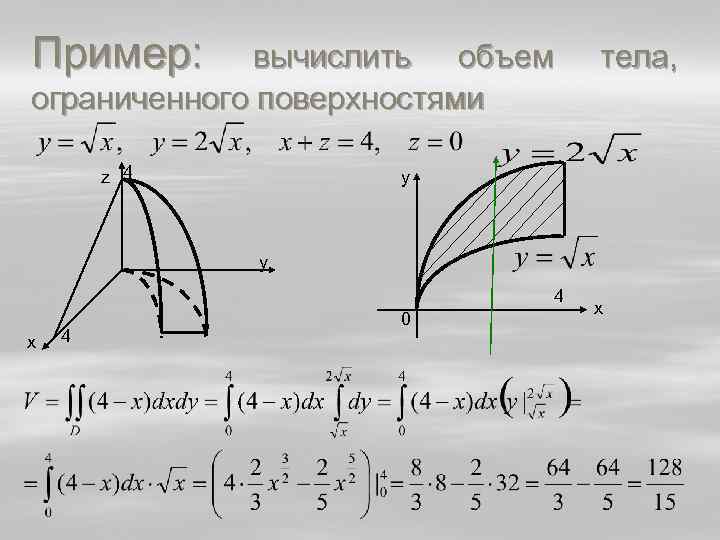Пример: вычислить объем ограниченного поверхностями z 4 тела, y у 4 х 4 0 x

Площадь поверхности тела Если поверхность задана уравнением z=f(x; y), где функция z=f(x; y) и ее частные производные первого порядка непрерывны в области D, тогда площадь этой поверхности равна

Пример: вычислить площадь части поверхности параболоида z=xy, принадлежащей цилиндру

Масса плоской пластины Если плоская пластина D имеет поверхностную плотность распределения масс непрерывную в D, то масса пластины вычисляется по формуле

Моменты инерции § Моменты инерции плоской материальной пластины D с поверхностной плотностью относительно координатных осей Ox, Oy и начала координат О(0; 0) соответственно вычисляются по формулам: § В случае однородной пластины принимают простой вид: эти формулы

Координаты центра тяжести § Координаты центра тяжести материальной пластины D с плотностью вычисляются по формулам где - статистические моменты пластины D относительно осей Ох и Оу соответственно, а m - ее масса § В случае однородной пластины соответственно имеем: