ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ Глава 4 34 стр

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ. Глава 4 , § 34, стр. 177

ТЕМА: УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ. § 34

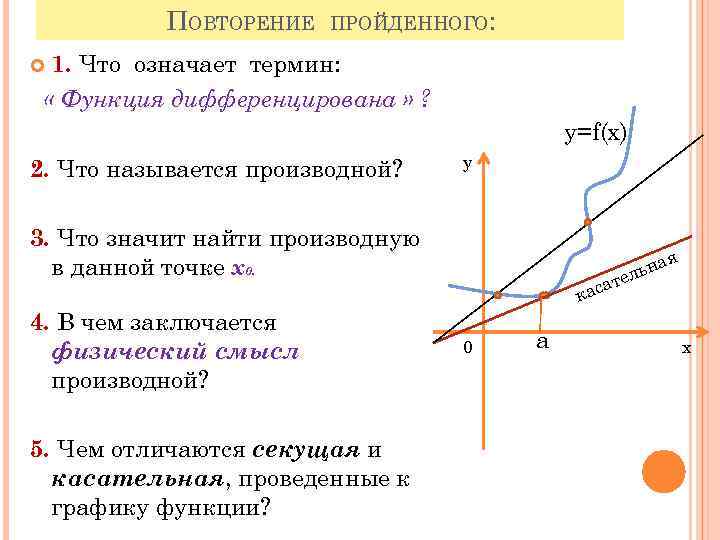ПОВТОРЕНИЕ ПРОЙДЕННОГО: 1. Что означает термин: « Функция дифференцирована » ? у=f(х) 2. Что называется производной? у 3. Что значит найти производную в данной точке х0. 4. В чем заключается физический смысл производной? 5. Чем отличаются секущая и касательная, проведенные к графику функции? т аса к 0 а я ьна ел х

ПОВТОРЕНИЕ ПРОЙДЕННОГО графики функций у=2 х+1 и у=-2 х+1 Описать их свойства (Возрастание, убывание) Построение. Построить

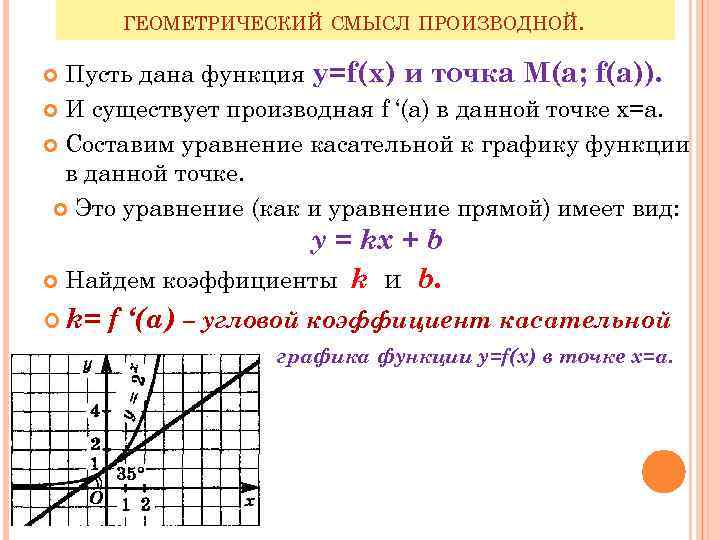ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. Пусть дана функция у=f(х) и точка М(а; f(а)). И существует производная f ‘(а) в данной точке х=а. Составим уравнение касательной к графику функции в данной точке. Это уравнение (как и уравнение прямой) имеет вид: у = kх + b Найдем коэффициенты k и b. k= f ‘(а) – угловой коэффициент касательной графика функции у=f(х) в точке х=а.

Т. к. точка М(а; f(а)) є графику функции, то ее координаты удовлетворяют графику функции ( или уравнению прямой): у = kх + b Подставим координаты в уравнение прямой: f(а) = kа + b b= f (а) - kа Подставим k и b в уравнение прямой: у = kх + b у= kx + f(а) -kа = f(а) + k(x-a) Т. к. k= f ‘(а) – угловой коэффициент касательной, то уравнение касательной к графику функции у=f(x) в точке х=а имеет вид: у= f(а) + f ‘(а)(x-a)

ЗАДАНИЕ-1. СОСТАВИТЬ УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=Х²В ТОЧКЕ Х=1. Решение. 1. 2. 3. Т. к. точка касания х=1, то а=1. f(a)= f´(x)= f´(a)= 4. Подставим найденные коэффициенты а, f(a), f´(a) в уравнение касательной у= f(а) + f ‘(а)(x-a) у= Ответ: уравнение касательной имеет вид : у=

Задание-2. Составить уравнение касательной к графику функции у=tgх в начале координат. • Решение. 1. Т. к. точка касания х=0, то а=0. 2. f(a)= 3. f´(x)= f´(a)= 4. Подставим найденные коэффициенты а, f(a), f´(a) в уравнение касательной у= f(а) + f ‘(а)(x-a) у= Ответ: уравнение касательной имеет вид: у=

Задание-3. Составить уравнение касательной к графику функции у=1/х в точке х=1. • Решение. 1. Т. к. точка касания х=1, то а=1. 2. f(a)= f(1)= 3. f´(x)= (1/x) ´= f´(a)= f´(1)= 4. Подставим найденные коэффициенты а, f(a), f´(a) в уравнение касательной у= f(а) + f ‘(а)(x-a) у= Ответ: уравнение касательной имеет вид: у=