Применение производной для исследования функций Обобщение темы § 30 -32
1. Найдите наибольшее значение функции • 1 вариант • 2 вариант 2. Представьте число 12 в виде суммы двух неотрицательных слагаемых, так чтобы их произведение было наибольшим • сумма их квадратов была наименьшей
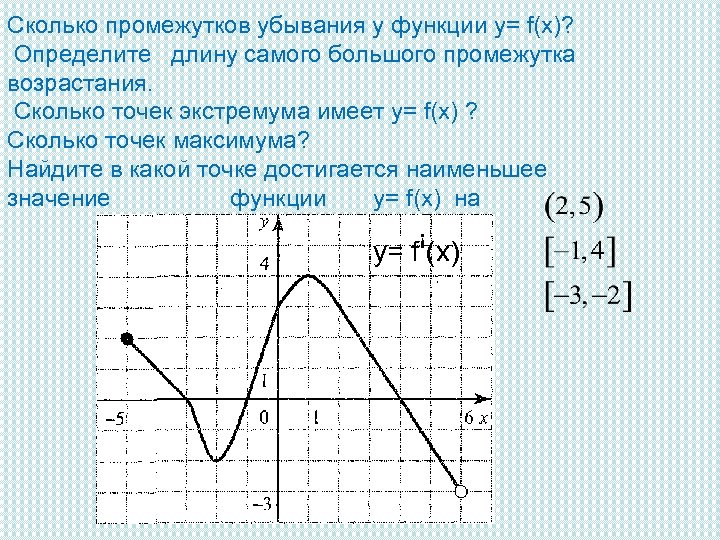
Сколько промежутков убывания у функции у= f(x)? Определите длину самого большого промежутка возрастания. Сколько точек экстремума имеет у= f(x) ? Сколько точек максимума? Найдите в какой точке достигается наименьшее значение функции у= f(x) на у= fꜞ(x)
Алгоритм исследования непрерывной функции y= f (x) на монотонность и экстремумы 1. Найти область определения y=f (x) : D(f) 2. Найти производную: f '(x) 3. Разложить f '(x) на множители 3. Найти а) f '(x) = 0 - стационарные точки б)f '(x) не существует- критические 4. Отметить стационарные и критические точки на D(f) и определить знаки производной на получившихся промежутках. 5. По знакам производной найти промежутки монотонности и точки экстремума
• • • План построения графика функции или алгоритм исследования функций Найти: область определения функции, если необходимо- асимптоты (горизонтальные и вертикальные), точки пересечения с осями координат, четность, нечетность периодичность, производную, критические и стационарные точки, точки экстремума и экстремумы функции, промежутки монотонности, множество значений функции, при необходимости- промежутки знакопостоянства, дополнительные точки.
Признаки монотонности • Признак возрастания • Признак убывания функции Если f'(x)≥ 0, то функция возрастает на промежутке Х. Если f'(x) ≤ 0, то функция убывает на промежутке Х.
Свойство экстремума Если функция имеет экстремум в точке х = х 0, то в этой точке f '(x 0) = 0 или f '(x 0) не существует. • Стационарные точки- • Критические точки это внутренние точки области определения, в • в которых f непрерывна, которых f '(x) = 0 но f '(x) не существует.
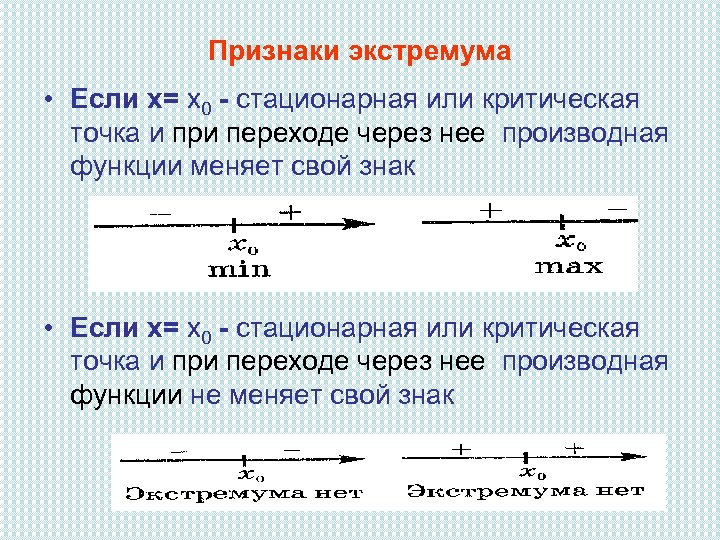
Признаки экстремума • Если х= х0 - стационарная или критическая точка и при переходе через нее производная функции меняет свой знак • Если х= х0 - стационарная или критическая точка и при переходе через нее производная функции не меняет свой знак
Асимптоты • Горизонтальные • Вертикальные Если y = p(x) : q(x) и Если lim f(x) = b, то x→ ∞ y = f(x) имеет горизонтальную асимптоту y= b. при х=а q(x)=0, то х=а- вертикальная асимптота • Полюсы функции y = p(x) : q(x), • Точки разрыва –это точки, где q(x)=0.
Нахождение наибольшего и наименьшего значений непрерывной функции 1. Теоремы о монотонной функции на отрезке 2. Метод оценки значений 3. Алгоритм для непрерывной функции на отрезке 4. Алгоритм для непрерывной функции на отрезке или на промежутке в случае, если у нее одна точка экстремума на этом промежутке.
![• Если функция возрастающая на отрезке [а, в], то наибольшее (наименьшее) значение на](https://present5.com/presentation/b20a12f04bf8d45ae4c2a9f77d20dfc6/image-11.jpg "• Если функция возрастающая на отрезке [а, в], то наибольшее (наименьшее) значение на")
• Если функция возрастающая на отрезке [а, в], то наибольшее (наименьшее) значение на отрезке [а, в] она достигает в… • Если функция убывающая на отрезке [а, в], то наибольшее ( наименьшее) значение на отрезке [а, в] она достигает в…
![Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у= f(x) на отрезке [a, b]](https://present5.com/presentation/b20a12f04bf8d45ae4c2a9f77d20dfc6/image-12.jpg "Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у= f(x) на отрезке [a, b]")
Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у= f(x) на отрезке [a, b] • 1. Найти производную f |(x) и разложить ее на множители • 2. Найти стационарные и критические точки функции • 3. Выбрать те из них, которые лежат внутри отрезка [a, b] • 4. Вычислить значения функции у = f(x) в точках, отобранных в пункте 3 и на концах отрезка- в точках aиb • 5. Выбрать среди этих значений наименьшее ( это будет у наим. ) и наибольшее ( это будет у наиб. )
Алгоритм отыскания наименьшего или наибольшего значений непрерывной функции у= f(x) на промежутке Х, если она имеет внутри него единственную стационарную или критическую точку • Найти производную и разложить ее на множители. • Найти стационарные и критические точки. • Выбрать ту из них, которая принадлежит заданному промежутку. • Определить вид экстремума в этой точке. • Определить наименьшее или наибольшее значение непрерывной функции на основании теоремы
Алгоритм отыскания наименьшего или наибольшего значений непрерывной функции у= f(x) на промежутке Х, если она имеет внутри него несколько стационарных или критических точек • Найти производную и разложить ее на множители • Найти стационарные и критические точки • Определить вид экстремумов • Найти значения функции в этих точках • Построить график функции • Сделать вывод
Задачи на отыскание наибольших и наименьших величин - задачи на оптимизацию 1. Составление математической модели. 2. Работа с составленной моделью. 3. Ответ на вопрос задачи.
Алгоритм решения задач на оптимизацию 1. Найти оптимизируемую величину (О. В. )и обозначить ее буквой Y или S, V, R. 2. Выбрать независимую переменную х 3. Выразить оптимизируемую величину Y (S, V, R) через х. 4. Установить границы изменения независимой переменной х (Х). 5. Найти наибольшее или наименьшее значение О. В. по алгоритмам- отыскать наибольшего или наименьшего значения функции у=f(х) с областью определения Х 6. Проанализировать полученные результаты и дать конкретный ответ на вопрос задачи.
АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x) в точке х=а 1. Записать уравнение касательной у = f(а) + f (а) (x – а) 2. Обозначить абсциссу точки касания буквой а (или х0 ). 2. Вычислить f(а). 3. Найти f (x) и вычислить f (а). 4. Подставить найденные числа а , f(а), f (а) в формулу у = f(а) + f (а) (x – а)
Скачать презентацию Применение производной для исследования функций Обобщение темы
b20a12f04bf8d45ae4c2a9f77d20dfc6.ppt