Применение неравенств в исследовании устойчивости разностных динамических

«Применение неравенств в исследовании устойчивости разностных динамических систем» Ким Екатерина Лян Анастасия Ученицы 12 С НИШ г. Талдыкорган

ЦЕЛЬ РАБОТЫ: Получить различные дискретные неравенства и систематизировать различные типы дискретных неравенств, используемых в теории устойчивости РДС, а также показать область их применения.

Актуальность работы и Научная новизна исследования

Лемма о дискретном аналоге неравенства Беллмана

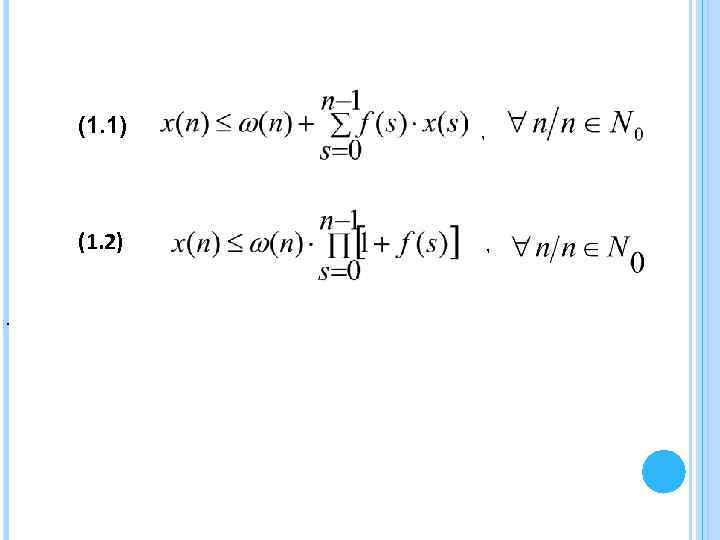(1. 1) (1. 2). , ,

Теорема 1 Если выполняется неравенство (1. 3) , то справедливо неравенство (1. 4) , .

Применение дискретных неравенств к исследованию РДС

Оценки решения нелинейных разностных динамических систем

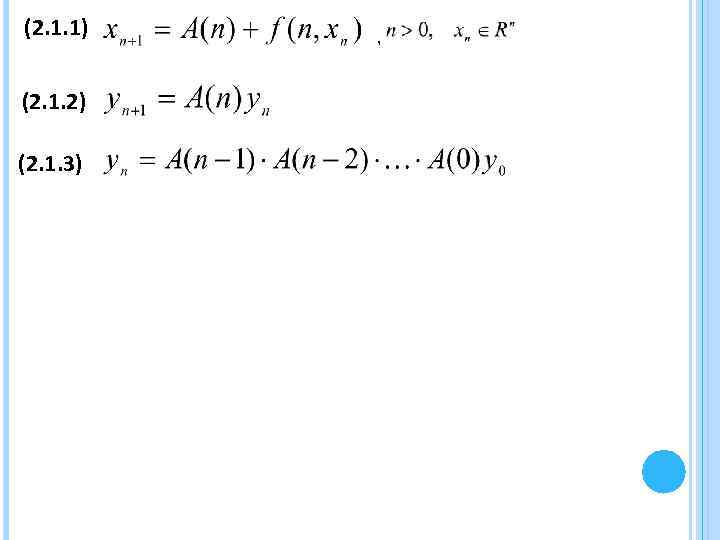(2. 1. 1) (2. 1. 2) (2. 1. 3) ,

Обозначим (2. 1. 4) Теперь возьмем некоторую функцию так как то , тогда получим

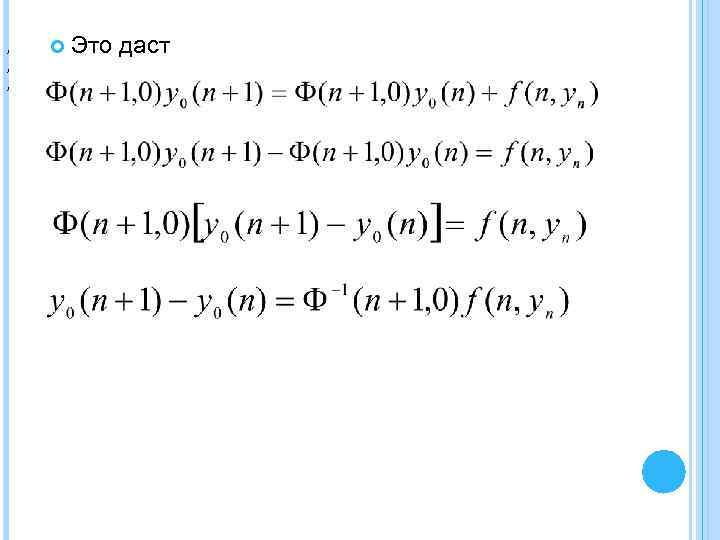, , , Это даст

. Варьируя по n получим (2. 1. 5) где Подставим (2. 1. 5) в (2. 1. 4), получим

По свойству модуля имеем Пусть вектор функция удовлетворяет условию (2. 1. 6) где , - некоторое положительное число, - сколь угодно малое положительное число, тогда получим следующее неравенство

Введем обозначения. , и получим , где Применяя лемму 1, получим следующую оценку (2. 1. 7) где так как (2. 1. 8) , то

Теорема 2. 1. 1 Если нелинейная часть РДС (2. 1. 1) в окрестности начала координат удовлетворяет условию (2. 1. 6), то ее решение оценивается сверху неравенством (2. 1. 8). Получены некоторые новые дискретные неравенства, которые позволяют судить об устойчивости РДС

ТЕОРЕМА 2. 1. 2 Пусть, Если при (2. 1. 9) тогда , - неотрицательные функции. выполняется неравенство

Доказательство: Отметим Положим Очевидно, что. Из того, что , тогда при

находим Умножая обе части неравенства 2. 1. 13 на и учитывая, 2. 1. 11 преобразуем его. Получим оценку (2. 1. 14) Далее, пусть. Преобразуем левую часть неравенства (2. 1. 14) к виду (2. 1. 15)

где D - некоторое значение, находящееся между и Из того, что - неубывающая, а - невозрастающая, следует если

и если Из 2. 1. 13 и 2. 1. 15 получаем (2. 1. 16) при Учитывая, что до n+1 находим (2. 1. 17) при , и суммируя (2. 1. 16) по n от 0

Из оценки (2. 1. 17) получаем (2. 1. 18) При Учитывая, что и из неравенства (2. 1. 18) находим оценку (2. 1. 10). Таким образом, теорема доказана.

Теорема 2. 1. 2 Пусть функция - непрерывная положительная и неубывающая на Если при имеет место неравенство (2. 1. 19) то , при , а также

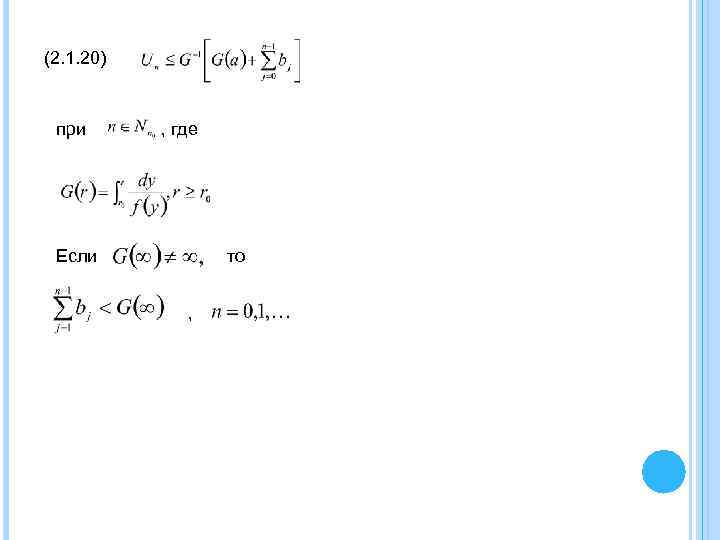(2. 1. 20) при , где Если то ,

Доказательство: Определим последовательность формулой рекуррентной (2. 1. 21) очевидно, что (2. 1. 22) - удовлетворяет уравнению

Из (2. 1. 19), (2. 1. 21) и (2. 1. 22) получаем причем. Отсюда по свойству функции находим (2. 1. 23) при Суммируя обе части неравенства (2. 1. 23) по от 0 до получаем

отсюда Теорема доказана. Отсюда пусть Тогда из неравенства (2. 1. 24) и того, что , , ,

, следует оценка (2. 1. 25) В работе получено одно неравенство типа Гронуолла, которое применяется для оценки решения нелинейных разностно-динамических систем с помощью фундаментальных решений линейного приближения.

Теорема 2. 1. 3 Пусть функции , - непрерывны и функции , - суммируемы, предположим, что , неотрицательны на N и удовлетворяют неравенству (2. 1. 26) , тогда справедливо неравенство (2. 1. 27) ,

(2. 1. 29) , Зададим функцию равенством (2. 1. 30) , отсюда , учитывая (2. 1. 27) имеем

Доказательство : Обозначим (2. 1. 28) очевидно, что , Отметим, что умножив обе части неравенства на получим: , в свою очередь получим

то есть. , или Отсюда Суммируем по n от (2. 1. 31) до n-1 , получим

Из (2. 1. 31) следует Отсюда Значение подставим в (2. 1. 26), получим (2. 1. 27). Теорема доказана. Рассмотрим разностную динамическую систему (РДС)

(2. 1. 32) где , - невырожденная , матрица, ; Представим решение виде РДС (2. 1. 32)в следующем (2. 1. 33) где линейной РДС: фундаментальная матрица

Из соотношения , где - некоторое положительное число, , , - сколь угодно малое положительное число, получим следующее неравенство ,

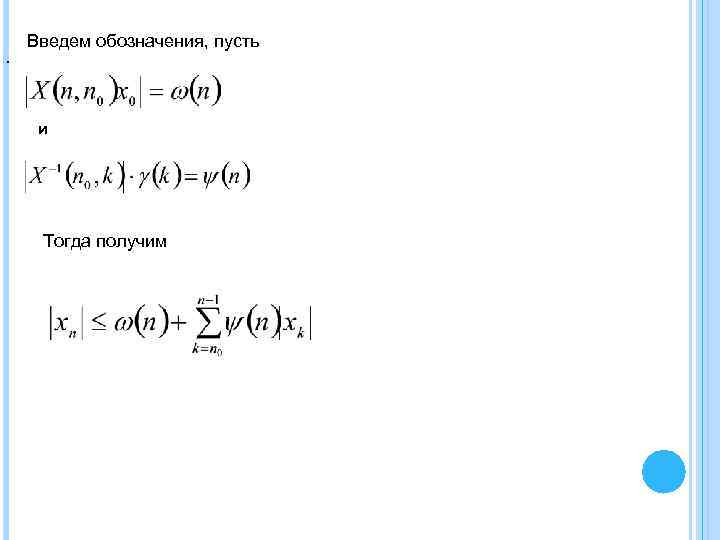Введем обозначения, пусть. и Тогда получим

Теорема 2. 1. 4 Пусть функция - непрерывна и функция - суммируема. Предположим, что - неотрицательна на N и удовлетворяют неравенству тогда справедливо неравенство

Доказательство: Применяя теорему 2. 1. 4, получим оценку Из этого неравенства следует утверждение теоремы.

Теорема 2. 21 ( об устойчивости РДС по первому приближению)

Если все собственные значения матрицы имеют значения по модулю меньшие единицы, то положение равновесия РДС (2. 2. 1) экспоненциально устойчиво. Доказательство: Мы будем доказывать экспоненциальную устойчивость нулевого решения РДС ( ), что эквивалентно утверждению теоремы. Требуется найти такие положительные , чтобы из неравенств , следовало неравенство

Для функции по известной формуле оператора сдвига 2. 1. 13 для линейной неоднородной РДС мы можем получить из Теперь учитывая , что получим оценку

Применив условие положительное , выберем по любому так, чтобы из неравенства неравенство Пусть на интервале Тогда при следовало . справедливо неравенство

Следовательно, функция удовлетворяет следующему неравенству По аналогу леммы Гронуолла-Беллмана 2. 1. 12 получаем Для функции это дает где

, Зафиксируем теперь условий , где так, чтобы было , выбирается по так, как показано выше. Покажем, что константы Пусть , тогда и являются искомыми. , так как Рассмотрим максимальный полуинтервал на котором сохраняется неравенство (2. 2. 2) и заметим, что . Выберем, наконец, . . из

Действительно. Если это не так, то на отрезке выполняется (2. 2. 1), откуда следует сохранение (2. 2. 2) в точке n 1. Итак, (2. 2. 2) выполнено на множестве выполняется и (2. 2. 2). Теорема доказана. , но тогда на этом

Теорема 2. 2. 3 Пусть решение РДС (2. 3. 1) существует на N , где A - постоянная матрица, f и g непрерывны и ограничены на при. Предположим, что а) матрица имеет все б) равномерно по при достаточно малом значении выполняется соотношение

в) для любого положительные числа и такие, что при . Тогда существует решения такое, что при достаточно малом. Доказательство: Линейное преобразование (2. 3. 2) где приводит РДС (2. 3. 1) к виду

Суммируя по n от 0 до n-1 , получим Подставляя в (2. 3. 2), получим или (2. 3. 3) ) Так как (2. 3. 4) И (2. 3. 5 при

то применяя (2. 3. 4) и (2. 3. 5) к (2. 3. 3) получим Применяя к последнему дискретный аналог неравенства Гронуолла получим: , где Учитывая, что . , приходим к оценке: . Отсюда и следует доказательство существования достаточно малом решения при , что при.

Результаты исследования: некоторые новые дискретные неравенства, которые позволяют судить об устойчивости РДС; одно неравенство типа Гронуолла, которое применяется для оценки решения нелинейных разностно-динамических систем с помощью фундаментальных решений линейного приближения; результат об устойчивости по первому приближению решения разностной динамической системы по предположениям относительно нелинейности;

Вывод: В работе проведено исследование, при котором решение оценивается функциями, зависящими от известных параметров, входящих в правые части РДС. При этом были систематизированы различные типы дискретных неравенств, используемых в теории устойчивости РДС. Эти задачи до сих пор не были проработаны и поэтому полученные результаты представляют теоретическую и практическую ценность и важны в приложениях, а также будут полезны для дальнейшего развития теории устойчивости РДС.