Применение линейного программирования для принятия решения о сокращении

Применение линейного программирования для принятия решения о сокращении Поиск самого дешевого способа сокращения работы можно трансформировать в форме линейного программирования: Пусть Z = общая стоимость сокращения работ. Задача состоит в том, чтобы свести Z к минимуму, с учетом того ограничения, что продолжительность проекта должна быть ≤ желаемым срокам по мнению руководителя проекта.

xj = время на которое сокращаем работу j , для j = A, B. . . , N. Используем последний столбец колонки целевая функция для минимизации: Z = 100, 000 x. A + 50, 000 x. B +… + 60, 000 x. N. Переменные решения должны быть ограничены: они должны иметь неотрицательные значения и не превышать максимум. Применяем: Продолжительность проекта должна быть ≤ нужному значению (40 недель), пусть y. FINISH = длительность проекта, т. е. время, за которое достигается конечный узел ограничение: y. FINISH ≤ 40.

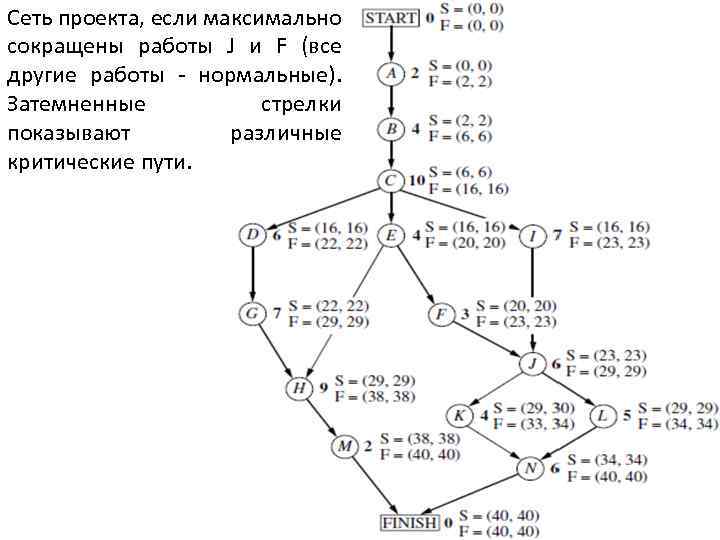Сеть проекта, если максимально сокращены работы J и F (все другие работы - нормальные). Затемненные стрелки показывают различные критические пути.

Чтобы назначить соответствующее значение для y. FINISH, при известных значениях x. A, x. B, . . . , x. N, вводятся следующие дополнительные переменные: yj = начальное время работы j (для j = B, C, . . . , N) (не требуется для работы А, так как начальной работе автоматически присваивается значение 0). Рассматривая конечный узел как работу (хотя и с нулевой длительностью), это определение yj для конечной работы также подходит под определение y. FINISH. Начальное время каждой работы (в том числе и конечной) напрямую связано с начальным временем и продолжительностью предшествующей ей работы. Для каждой работы (B, C, . . . , N, конечной) и каждой из предшествующей ей работ, начальное время этой работы ≥ (начальному времени + продолжительность) предшествующей ей работы. Используя обычные сроки, продолжительность каждой работы определяется по следующей формуле: Продолжительность работы j = ее нормальное время - xj,

Работа, предшествующая работе F : работа Е, с продолжительностью = 4 - x. E. Отношения между этими работами: y. F ≥ y. E + 4 - x. E. работа F не может начаться до тех пор, пока не начнется и не завершится работа E с продолжительностью 4 - x. E. Работы, предшествующие работе J: Работа F с продолжительностью = 5 - x. F. Работа I с продолжительностью = 7 - x. I. Отношения между этими работами: y. J ≥ y. F + 5 - x. F, y. J ≥ y. I + 7 - x. I. работа j не может начаться, пока не завершатся предшествующие работы

Модель линейного программирования: Минимизировать: Z = 100, 000 x. A + 50, 000 x. B +… + 60, 000 x. N, С учетом: 1. Ограничения максимального сокращения: x. A ≤ 1, x. B ≤ 2, . . . , x. N ≤ 3. 2. Ограничения неотрицательности: x. A ≥ 0, x. B ≥ 0, . . . , x. N ≥ 0 y. B ≥ 0, y. C ≥ 0, . . . , y. N ≥ 0, y. FINISH ≥ 0. 3. Ограничения начального времени: одно ограничение (кроме как для A, с которой начинается проект) для работ с одной предшествующей работой (B, C, D, E, F, G, I, K, L, M), 2 ограничения для работ с 2 предшествующими работами (H, J, N, FINISH): 4. Ограничение продолжительности проекта y. FINISH ≤ 40

Эта задача может быть сформулирована в виде модели линейного программирования в таблице. Решения приведены в изменяемых ячейках, I 6: J 19 and J 21. Столбцы от B до H соответствуют столбцам таблицы. Уравнения для столбца К отражают, что конечное время каждой работы = ее начальному времени + нормальная продолжительность - уменьшение ее продолжительности вследствие ее сокращения. Уравнение в ячейке J 22 складывает все нормальные затраты плюс дополнительные расходы в связи с сокращениями, так получаем общую стоимость. Последний набор ограничений в диалоговом окне Поиск решения (Solver) (J 6: J 19 ≤ G 6: G 19) уточняет, что сокращение времени для каждой работы не может превышать максимального сокращения времени, приведенного в колонке G. Два предыдущих ограничения (J 21 ≥ K 18 и J 21 ≥ K 19 ) показывают, что проект не может закончиться, пока не завершится каждая из предшествующих работ (работы М и N). J 21 ≤ 40 указывает, что проект должен завершиться в течение 40 недель.

Ограничения, связанные с ячейками I 7: I 19 являются ограничениями начального времени, устанавливающими, что работа не может начаться, пока не закончатся все предшествующие работы, например, первое ограничение (I 10 ≥ K 8) показывает, что работа E не может начаться, пока не закончена работа С (предшествующая ей работа). Когда для работы существует более , чем одна предшествующая работа, для каждой из них существует одно такое ограничение. Для работы H имеются предшествующие работы E и G работа H имеет 2 ограничения начального времени, I 13 ≥ K 10 and I 13 ≥ K 12. Форма ≥ для ограничений начального времени допускает задержку начала работы после того, как закончились предшествующие ей работы. Хотя такая задержка в модели и возможна, она не может быть оптимальной для любой работы на критическом пути, так как эта задержка увеличивает общий объем расходов (требуя дополнительных сокращений для выполнения проекта в срок) оптимальное решение не будет иметь такие задержки, за исключением работ, которые не лежат на критическом пути.

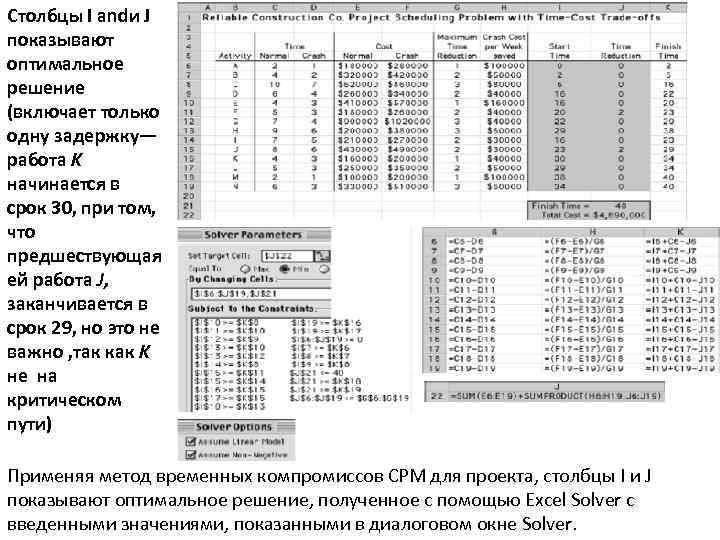Столбцы I andи J показывают оптимальное решение (включает только одну задержку— работа K начинается в срок 30, при том, что предшествующая ей работа J, заканчивается в срок 29, но это не важно , так как K не на критическом пути) Применяя метод временных компромиссов CPM для проекта, столбцы I и J показывают оптимальное решение, полученное с помощью Excel Solver с введенными значениями, показанными в диалоговом окне Solver.

Выводы менеджера: Когда сотрудники приносят план сокращения проекта с 44 до 40 недель, менеджер смотрит на предполагаемую общую стоимость = $4. 69 млн. Полная сметная стоимость без сокращения = $4. 55 млн, дополнительные расходы на сокращение = $ 140, 000, это на $ 10, 000 <бонуса = $ 150, 000, если закончить в течение 40 недель. Существует неопределенность в отношении того, сколько времени потребуется для каждой работы и проекта в целом. Метод PERT 3 -х оценок привел к тому, что среднее значение распределения вероятностей продолжительности проекта (без сокращения) = 44 недель, но с большой дисперсией, того, что вероятность не закончить за 47 недель = 0, 2 (вызвав штраф в размере $ 300 000). При снижении среднего значения до 40 недель, есть столько же шансов, что фактическая длительность проекта превысит 40 недель. Зачем тратить дополнительные $ 140 000, чтобы получить 50%-ый шанс заработать бонус в размере $ 150 000?

Вывод 1: План по сокращению проекта дает вероятность = 0, 5 для завершения проекта в течение 40 недель, поэтому дополнительная стоимость плана ($ 140, 000) не оправдана любые сокращения на данном этапе отвергаются. Отмечаем, что 2 работы, которые было предложено сократить (F и J) приходятся примерно на середину проекта если проект идет со значительным опережением графика до работы F, то реализации плана сокращения почти наверняка позволит завершить проект до 40 недель. Закончить в этот срок было бы хорошо для репутации компании (и для менеджера лично).

Вывод 2: Дополнительные расходы на сокращение оправданы, если будет получен бонус = $ 150, 000 за завершение проекта в течение 40 недель план нужно держать в резерве, чтобы реализовать, если проект идет с опережением графика до работы F. Также существует возможность, что проект будет отставать от графика, и что придется платить штраф $ 300, 000, если не закончить за 47 недель. Если это происходит без применения сокращений, очевидно, что этого можно избежать путем сокращения работы J (это будет стоить = $ 30, 000 / неделю) и, при необходимости, сокращения работы F, а также (это будет стоить = $ 40, 000 / неделю). Это верно, если данные работы лежат на критическом пути после возникновения задержки.

Вывод 3: Дополнительные расходы (полные или частичные) на план по сокращению могут быть легко оправданы, если можно избежать штраф в размере $ 300 000 если не закончить проект в течение 47 недель План по сокращению должен быть в резерве, чтобы быть частично или полностью реализованы, если проект сильно отстает от графика до начала работ F или J. Нужно внимательно следить за графиком по мере развития проекта (и принять решение о сокращении), и за расходами, чтобы попытаться сохранить проект в рамках бюджета.

СОСТАВЛЕНИЕ ГРАФИКА И КОНТРОЛЬ РАСХОДОВ ПРОЕКТА • Расходы на составление графика • Расходы на контроль

Хороший руководитель проекта тщательно планирует и контролирует как время, так и расходы проекта. Важен как график, так и бюджет. Вопрос 9: Как следует контролировать текущие расходы, чтобы попытаться сохранить проект в рамках бюджета? Метод PERT / CPM , известный как PERT / Cost разработан специально для этой цели.

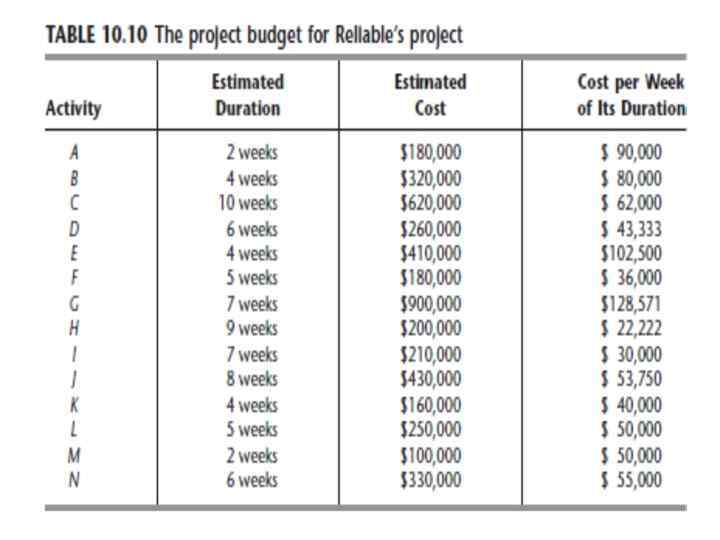
PERT/Cost : систематическая процедура, помогающая руководителю проекта планировать, составлять график и контролировать стоимость проекта. Она начинается с составления оценки расходов для каждой работы. При этом менеджер не планирует сокращение, поэтому сметные расходы на работы проекта в Таблице – нормальные значения. Эти расходы затем отображаются в бюджете проекта. Таблица также включает установленную длительность для каждой работы (столбец с обычными сроками), Стоимость каждой работы / ее продолжительность правый столбец Таблицы.

Предположение: при использовании PERT/Cost, затраты на выполнение работ равномерны на всем его протяжении. Менеджер делает это предположение, получаем сметную стоимость продолжительности работ для каждой недели в крайнем правом столбце таблицы. При применении PERT / Cost к более крупным проектам (многочисленные работы), обычно группы связанных друг с другом работ объединяют в «рабочие пакеты» . И бюджет проекта и график проекта (описанные далее) разрабатываются с точки зрения этих рабочих пакетов, а не отдельных работ. Менеджер решил не делать этого, так как проект включает только 14 работ.

Планирование расходов проекта: Менеджер должен знать, сколько денег требуется для покрытия расходов по проекту неделя за неделей. PERT/Cost предоставляет эту информацию посредством правого столбца таблицы 10. 10 чтобы разработать еженедельный график расходов, когда отдельные работы начинаются в самый ранний срок. Затем, чтобы показать, насколько гибкой является возможность задержки расходы, PERT / Cost делает то же самое, если отдельные работы начинаются в самый поздний срок. Чтобы это сделать, Excel файл включает в себя шаблон Excel (с маркировкой PERT Cost) для составления графика затрат проекта на срок до 45 периодов времени. (MS Project генерирует в основном ту же самую информацию, выбрав Таблица: Стоимость и Отчет в меню Вид, затем выбирая вариант Расходы. . . Cash Flow (отчета о денежных средствах). ) Это показано на рисунке 10. 14

Шаблон Excel (включая уравнения в ячейках результата) в начале проекта основан на самых ранних сроках начала (столбец B ), столбцы B, C, и D получаются непосредственно из таблицы. Рисунок показывает этот же шаблон для 17 – 25 недель. Работы D, E, и I имеют ранний срок начала - 16 (16 недель после начала проекта ) они начинаются на 17 -той неделе, к работам F и G приступают позже, во время, показанное на рисунке. Столбец W через AE показывает еженедельную стоимость (в долларах ) каждой из работ, полученную из колонки F , для длительности работы (заданной в колонке C). Строка 22 показывает сумму еженедельных расходов на работу для каждой недели. Строка 23 этого шаблона показывает общую стоимость проекта от 1 -й недели до указанной недели. Рассмотрим, например, неделю 17. До недели 17 , были завершены работы A, B, и C, но никакие другие работы не были начаты общая стоимость для первых 16 недель (из 3 -го столбца таблицы) = $180, 000 _ $320, 000 _ $620, 000 _ $1, 120, 000. Складываем еженедельные стоимости проекта до недели 17 $1, 120, 000 _ $175, 833 _ $1, 295, 833.

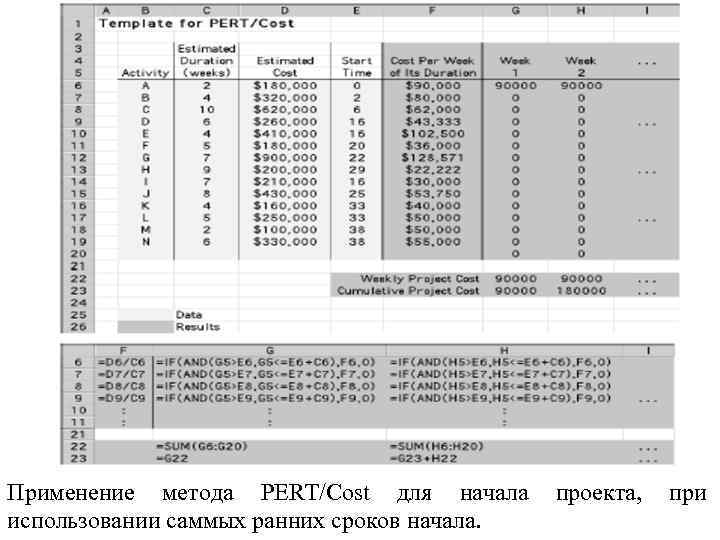Применение метода PERT/Cost для начала использовании саммых ранних сроков начала. проекта, при