bc67e850e126171755f33217d2438e6b.ppt
- Количество слайдов: 53

Primary Mathematics Subject Knowledge Course Day 4 - Algebra Developing teaching and learning in mathematics Hampshire Mathematics Advisory Team 1

“Algebra …” • What does the word conjure up in your own mind? • What are your thoughts and feelings about it? 2

Session 1 - The art of noticing … • • • What stays the same? What changes? How does it change? What patterns and relationships are there? How can these relationships be generalised? (in words first, then later with symbols) 3

Repeating patterns What would the 15 th shape be? What do you see? What do you notice? What colour would the 18 th square be? In what position is the 4 th black square? Hampshire Mathematics Advisory Team 4 4

Repeating patterns in context Mr Smith is laying a new path he is using a mixture of grey, white and pink slabs. Here is his pattern… How many pink slabs would he need if his path was – 24 slabs? – 40 slabs? – 100 slabs? How do you know? What colour is the 28 th slab? Hampshire Mathematics Advisory Team 5 5

Hidden sections 6

From counting to patterning • Jane’s dotty squares (NCETM) – Shady circles Pg 97 H. Cooke book 7
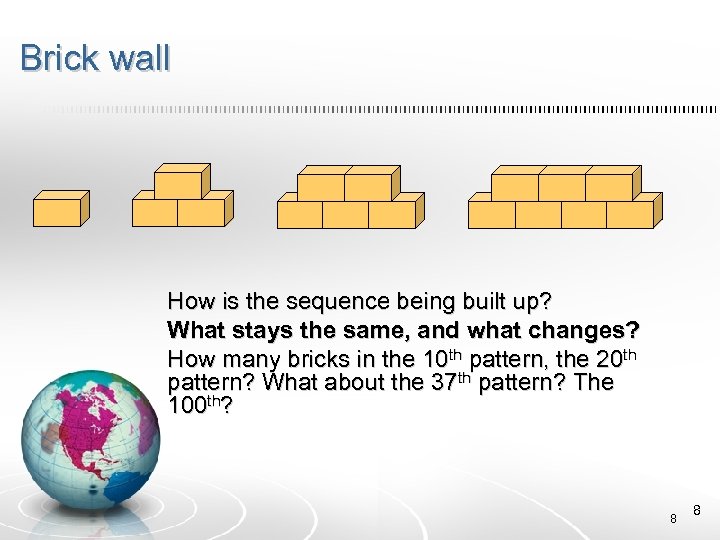
Brick wall How is the sequence being built up? What stays the same, and what changes? How many bricks in the 10 th pattern, the 20 th pattern? What about the 37 th pattern? The 100 th? 8 8
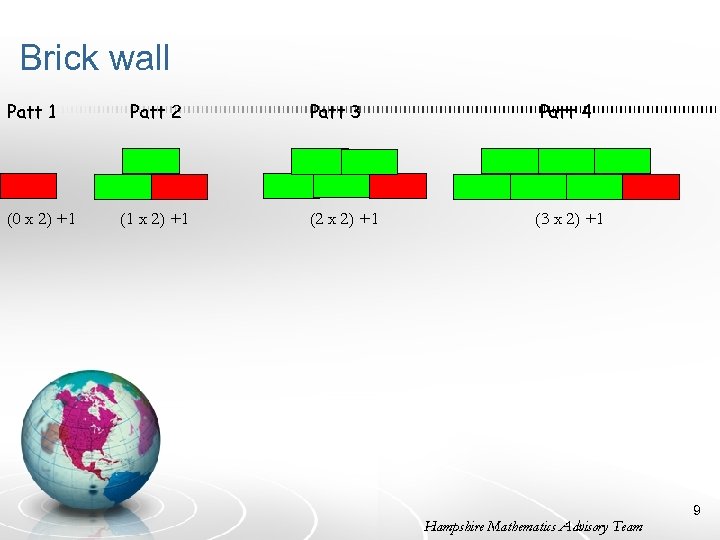
Brick wall Patt 1 (0 x 2) +1 Patt 2 (1 x 2) +1 Patt 3 Patt 4 (2 x 2) +1 (3 x 2) +1 Hampshire Mathematics Advisory Team 9
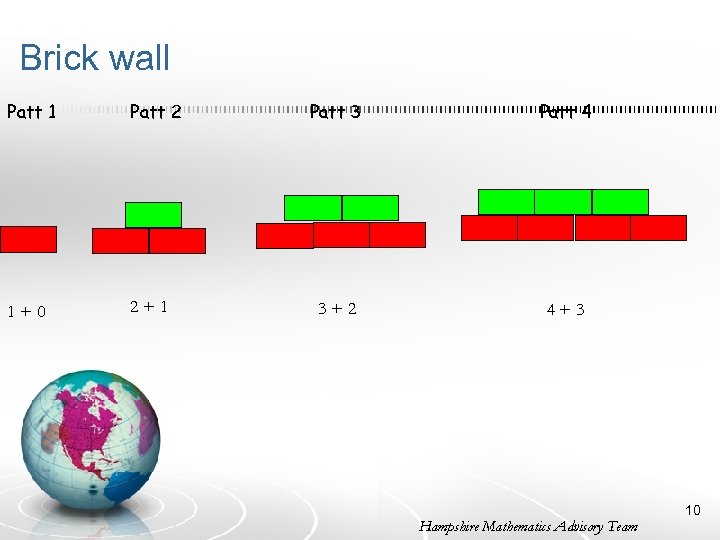
Brick wall Patt 1 Patt 2 1+0 2+1 Patt 3 Patt 4 3+2 4+3 Hampshire Mathematics Advisory Team 10
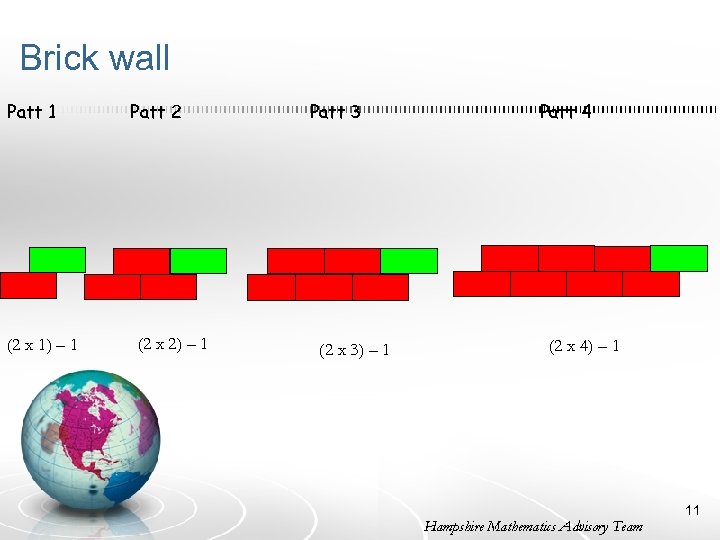
Brick wall Patt 1 (2 x 1) – 1 Patt 2 (2 x 2) – 1 Patt 3 (2 x 3) – 1 Patt 4 (2 x 4) – 1 Hampshire Mathematics Advisory Team 11
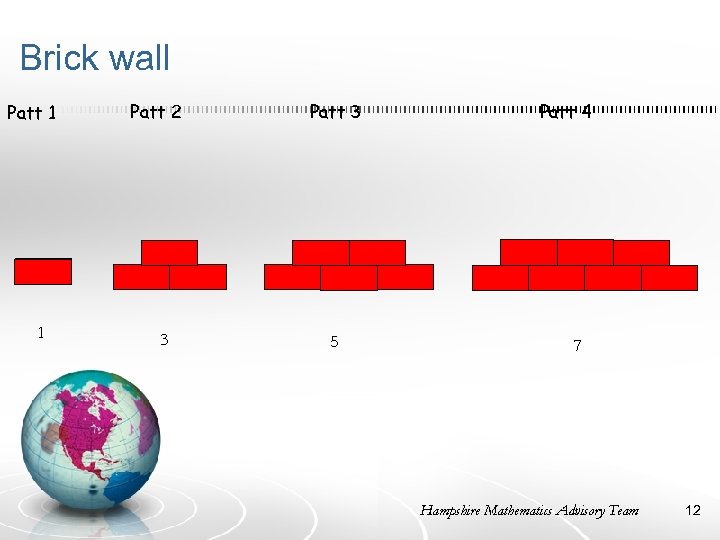
Brick wall Patt 1 1 Patt 2 3 Patt 3 5 Patt 4 7 Hampshire Mathematics Advisory Team 12
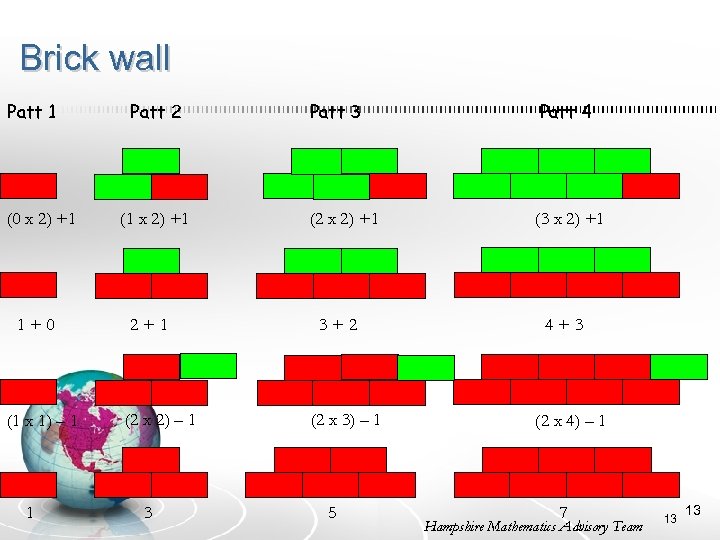
Brick wall Patt 1 (0 x 2) +1 1+0 (1 x 1) – 1 1 Patt 2 (1 x 2) +1 2+1 (2 x 2) – 1 3 Patt 4 (2 x 2) +1 (3 x 2) +1 3+2 (2 x 3) – 1 5 4+3 (2 x 4) – 1 7 Hampshire Mathematics Advisory Team 13 13

What next? Look at the sequences below. Predict the next three numbers 2, 4, 6, 8, 10, . . . 2, 5, 8, 11, 14, . . . 1, 1 , 2, 3, 5, 8, . . . Find a rule, in words, for working out the next term in each sequence based on: • the value of the previous term (or terms) • the term number (i. e. the position number) • Calculators – use of the constant function to generate sequences 14 14
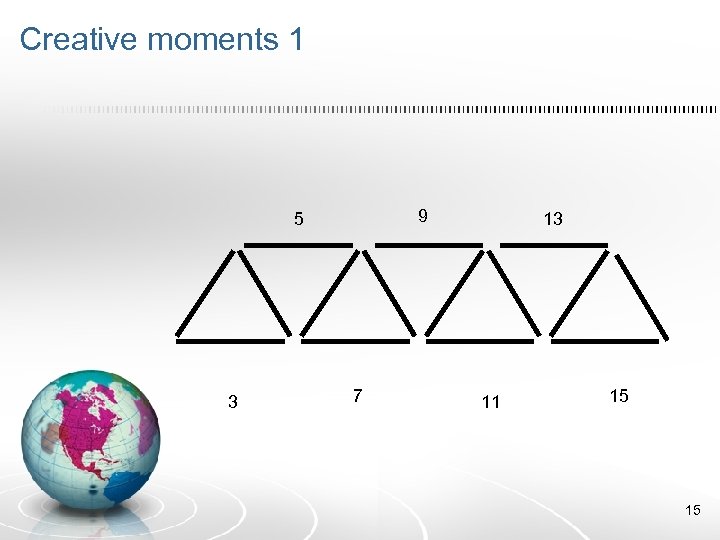
Creative moments 1 9 5 3 7 13 11 15 15
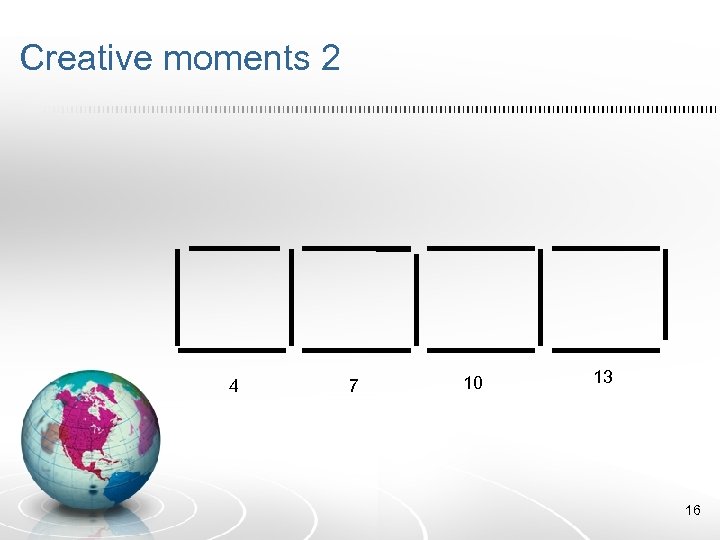
Creative moments 2 4 7 10 13 16

Algebraic links - graphing • Use the numbers in the sequences to create “coordinates” • What sort of “graph” is created? 17

Generating number sequences from diagrams • Array Creator files (Yvonne Excel) • What is the next diagram? • Think about how you draw the next one in the sequence? • What would this be recorded like as a calculation? • Are these all the same? (multiple expressions) 18

Chelsea Flower Show… • • • Simon Singer, a famous garden designer, has come up with a plan for a water feature in his showgarden. He decides it will be surrounded by 1 square metre square pink paving slabs But Simon can’t quite decide how long the water feature will be. . . 4 m, or 5 m, or maybe 12 m, or maybe even 53 m! How could he work out quickly how many paving slabs to order once he has decided on the length of the water feature? 19
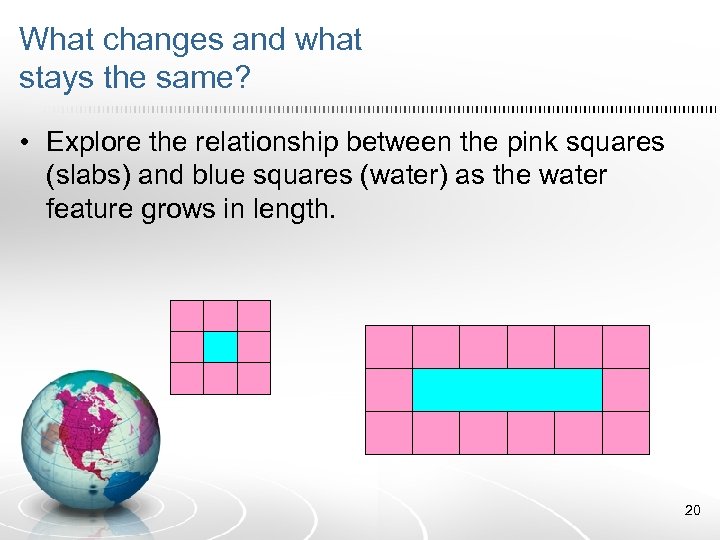
What changes and what stays the same? • Explore the relationship between the pink squares (slabs) and blue squares (water) as the water feature grows in length. 20

Chelsea Flower Show 2 • • • Later one of Simon’s friends suggests they change his design to an “L” shape water feature Another friend suggests they could make the water feature in the middle a square How would they work out the number of paving slabs needed if Simon still couldn’t quite decide how big the whole thing would be? 21
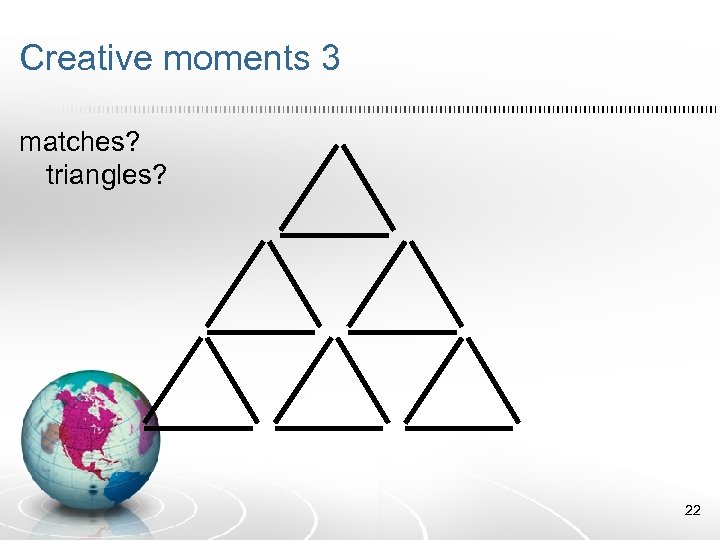
Creative moments 3 matches? triangles? 22
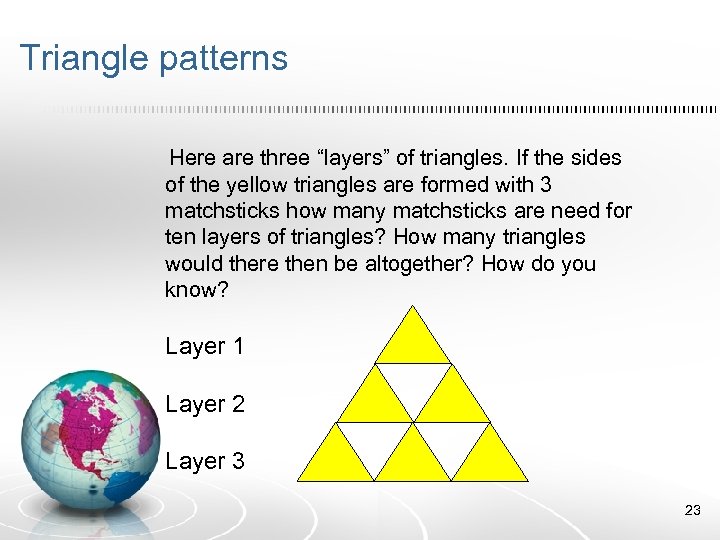
Triangle patterns Here are three “layers” of triangles. If the sides of the yellow triangles are formed with 3 matchsticks how many matchsticks are need for ten layers of triangles? How many triangles would there then be altogether? How do you know? Layer 1 Layer 2 Layer 3 23

Primary Numeracy Strategy • Look through the mathematical strands – Which objectives appear to relate to what we have been doing? 24

Lunch 25

Sharing session • Discuss the class-based task you tried out with your children • What did you find out about their knowledge and understanding of this aspect of mathematics? • What impact did the task(s) have? 26

Number patterns … • Specific sequences to be recognised • Multiples • Square numbers • Triangle numbers 27

Multiple expressions • What multiple expressions are there for calculating the perimeter of a rectangle? • • a + b + a + b a+b doubled 2 a + 2 b 2(a + b) 28

Using arrays • Create a 8 x 5 array • What multiple expressions are there to describe this array? 29
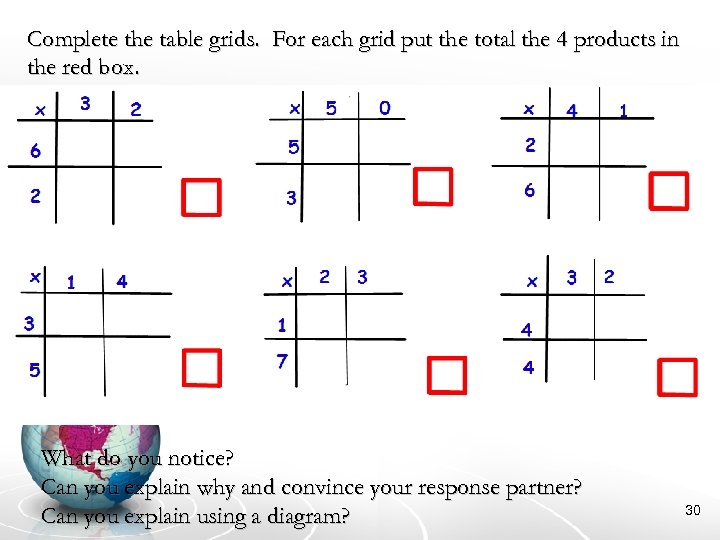
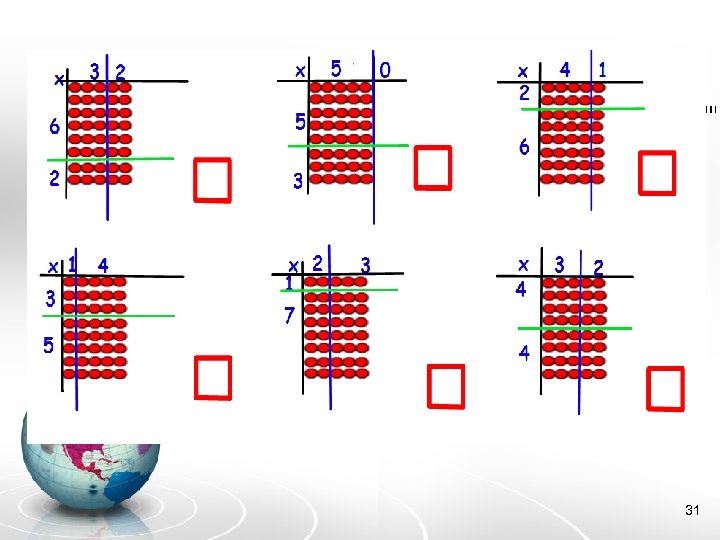
Complete the table grids. For each grid put the total the 4 products in the red box. What do you notice? Can you explain why and convince your response partner? Can you explain using a diagram? 30
31

Number sentences Hampshire Mathematics Advisory Team 32 32

What else can you work out from knowing that…. 9 + 3 = 12 6 x 3 = 18 8 – f = 3 a x b = 12 y – d = w Hampshire Mathematics Advisory Team 33 33

Families of four 2 + 3 = 5 a + b = c 3 + 2 = 5 3 + a = 5 b + a = c 5 – 2 = 3 5 – a = 3 c – a = b 5 – 3 = 2 5 – 3 = a c – b = a Hampshire Mathematics Advisory Team 34 34

Arrays – what do you see? 2 x 3=6 3 x 2=6 6÷ 3=2 6÷ 2=3 Hampshire Mathematics Advisory Team 35 35
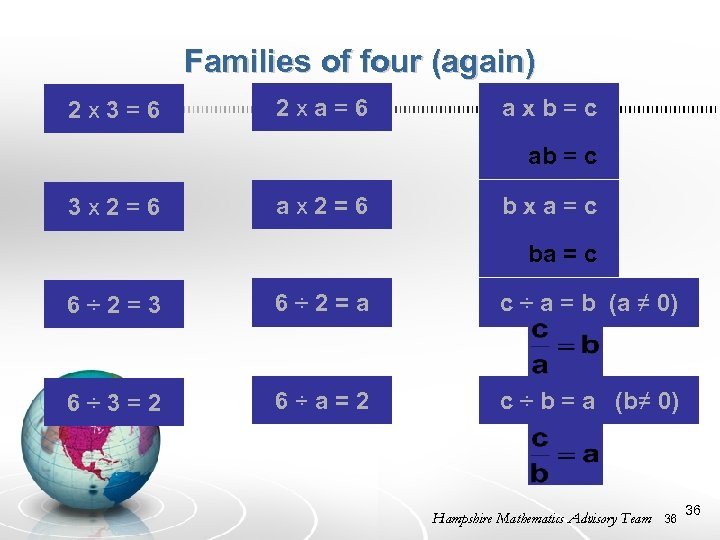
Families of four (again) 2 x 3 = 6 2 x a = 6 a x b = c ab = c 3 x 2 = 6 a x 2 = 6 b x a = c ba = c 6 ÷ 2 = 3 6 ÷ 2 = a c ÷ a = b (a ≠ 0) 6 ÷ 3 = 2 6 ÷ a = 2 c ÷ b = a (b≠ 0) Hampshire Mathematics Advisory Team 36 36

Aspects of algebra • • Marbles Packets of mints Algebra pairs Always sometimes never • Expressions or equations? 37

Aspects of algebra Mints A teacher has 5 full packets of mints and 6 single mints. The number of mints inside each packet is the same. The teacher tells the class: “Write an expression to show many mints there altogether. Call the number of mints inside each packet y” Here are some of the expressions that the pupils write: 5 + 6 + y 5 y 6 5 y + 6 5 + 6 y (5 + 6) x y 6 + 5 y Which expressions are correct, and why? 38

Aspects of algebra Bags of marbles !!! Jill took 2 marbles out of one of the bags, and none out of the other bags. Jill has 3 bags of marbles. Jill took 2 marbles out of each of the bags. Each bag has p marbles inside. Jill takes some marbles out. Now the total of marbles in Jill’s 3 bags is 3 p – 6 Some of the statements on the right could be true. Jill took 3 marbles out of one of the bags, and none out of the other bags. Jill took 3 marbles out each of two of the bags, and none out of the other bag. Put a tick by each statement which could be true. Jill took 6 marbles out of one of the bags, and none out of the other bags. Jill took 6 marbles out of each of two of the bags, and none out of the other bag. 39
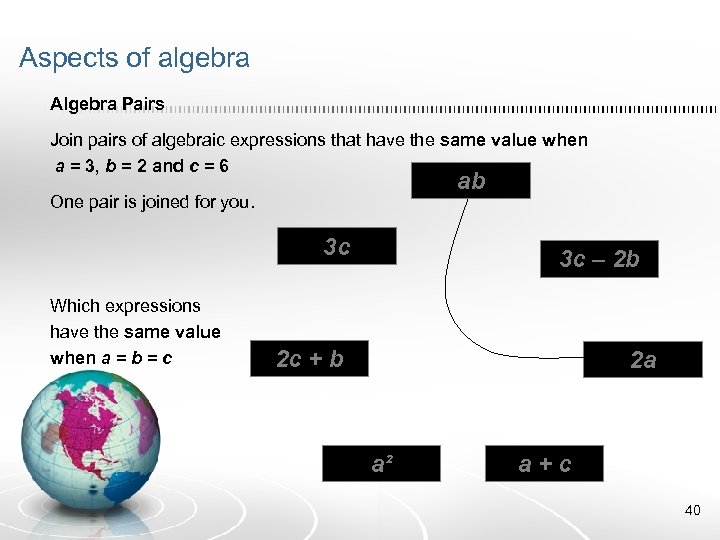
Aspects of algebra Algebra Pairs Join pairs of algebraic expressions that have the same value when a = 3, b = 2 and c = 6 ab One pair is joined for you. 3 c Which expressions have the same value when a = b = c 3 c – 2 b 2 c + b 2 a a² a+c 40

Aspects of algebra Sort these equations into ‘always true’, ‘sometimes true’ or ‘never true’: a + 5 = 12 b + 12 = b + 16 2 c + 3 = 3 + 2 c 2 d – 5 = 5 – 2 d f + 12 = g + 12 k + 5 < 20 4 + 2 e = 6 e p² = 10 p 3(m + 3) = 3 m + 3 4(3 + n) = 12 + 3 n 41

Bury the bone x = 2 2 x = 4 2 x + 5 = 9 (2 x + 5) = 3 (2 x + 5) - 6 = -3 3 Ref: Malcolm Swan Hampshire Mathematics Advisory Team 42 42
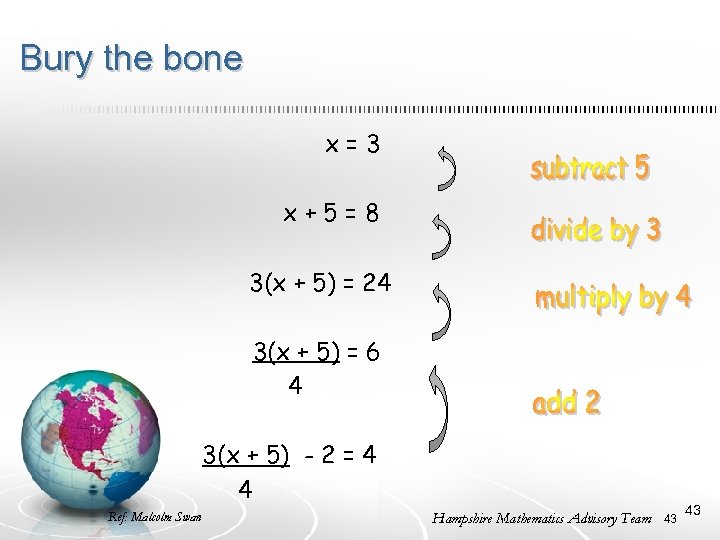
Bury the bone x=3 x+5=8 3(x + 5) = 24 3(x + 5) = 6 4 3(x + 5) - 2 = 4 4 Ref: Malcolm Swan Hampshire Mathematics Advisory Team 43 43

Power point problems • Can you identify the algebra that lies within the task? 44

Using Word Problems A(1) When two numbers are added together their total is 50. The difference between the numbers is 16. What are the two numbers? When two numbers are added together their total is 67. The difference between the numbers is 23. What are the two numbers? 45

Using Word Problems (A 2) Two people had £ 100 between them. The first person had £ 40 more than the second. How much did they each have? A bottle of orange juice and a glass together cost £ 1. 25. The bottle costs 35 p more than the glass. What is the price of the bottle? A man whose daughter was born when he was 36 have lived 100 years altogether between them. How old are they both? 46

Problems A(3) Two boxes of cornflakes have a total mass of 300 g. If 30 g is taken out of one box and put into the other box there would be the same amount of cornflakes in each box. How much does each box contain to begin with? I have put 720 marbles into three different sized bags. There are 80 more marbles in the biggest bag than in the smallest. There are 40 more marbles in the middle-sized bag than the smallest. How many marbles are there in each bag? 47

Problems B(1) Two people had £ 120 between them. The first person had 3 times more than the second. How much did they each have? A litre carton of apple juice and a bottle of Coca Cola together cost £ 2. 40. The apple juice costs four times as much as the Coca Cola. What is the price of the bottle of Coca Cola? 48

Problems (B 2) Jane’s age is 5 times Fred’s age. The sum of their ages is 54. How old are each of them? A farmer owns two farms. Their total area covers 225 square kilometres. One farm is 4 times as large as the other. How many square kilometres does each farm cover? 49

Problems (B 3) Sophie is 42 and Adam is 15. In how many years will Sophie be twice as old as Adam? Tim’s grandfather is now 87. Tim is 42. How many years ago was grandfather four times older than Tim? Alex is now twice as old as Ben. Seven years ago Ben was one third as old as Alex. How old are they both now? 50

Problems C(1) Buying tickets to the zoo for 1 adult and 4 children costs £ 19 and for 2 adults and 2 children costs £ 17. How much are the tickets? Six horses and five cows cost £ 180 and five horses and six cows cost £ 172. How much is each cow and each horse worth? 51

Problems C(2) Four lobsters cost a certain amount of money. If the price drops by £ 2 for each lobster I could buy 6 lobsters for the same price as 4. How much do the lobsters cost? A man has two horses, and a saddle worth £ 7. 50. If he puts the saddle onto the first horse it is then worth double the other. If he puts the saddle on the second horse it is worth £ 15 less than the first. What is the value of each horse? 52

Sharing session a) • Bring the work of one child … – What do you know about this child? – What level are they working at? (How do you know? ) – What are their strengths and weaknesses? – Do they have any identified barriers to learning? 53
bc67e850e126171755f33217d2438e6b.ppt