6319cbe17f31617ddccc0ef8fdd9a92a.ppt
- Количество слайдов: 25
 Приложно нелинейно програмиране ЛЕКЦИЯ 5 Нелинейно програмиране – Директни методи Prof. Boyan Bonev Ivanov, Ph. D. Email: bivanov@bas. bg Institute of Chemical Engineering-BAS
Приложно нелинейно програмиране ЛЕКЦИЯ 5 Нелинейно програмиране – Директни методи Prof. Boyan Bonev Ivanov, Ph. D. Email: bivanov@bas. bg Institute of Chemical Engineering-BAS
 Лекции Лекция 1 Въведение в математичното програмиране Лекция 2 Линейно програмиране Лекция 3 Оптимизация при целеви функции с един управляващ параметър Лекция 4 Нелинейно програмиране – Градиентни методи Лекция 5 Нелинейно програмиране – Директни методи Лекция 6 Нелинейно програмиране – Методи с ограничения Лекция 7 Методи за булева и дискретна оптимизация Лекция 8 Методи за глобална оптимизация Лекция 9 Методи за многоцелева оптимизация 2
Лекции Лекция 1 Въведение в математичното програмиране Лекция 2 Линейно програмиране Лекция 3 Оптимизация при целеви функции с един управляващ параметър Лекция 4 Нелинейно програмиране – Градиентни методи Лекция 5 Нелинейно програмиране – Директни методи Лекция 6 Нелинейно програмиране – Методи с ограничения Лекция 7 Методи за булева и дискретна оптимизация Лекция 8 Методи за глобална оптимизация Лекция 9 Методи за многоцелева оптимизация 2
 План на лекцията 1. Обща постановка на задачите на нелинейното програмиране без ограничения 2. Общ принцип на без градиентните методи за търсене на екстремум 3. Методи на сканирането 4. Метод на Гаус-Зайдел 5. Методи на случайното търсене 6. Симплексен метод за оптимизация 7. Предимства, недостатъци и област на приложение на без градиентните методи
План на лекцията 1. Обща постановка на задачите на нелинейното програмиране без ограничения 2. Общ принцип на без градиентните методи за търсене на екстремум 3. Методи на сканирането 4. Метод на Гаус-Зайдел 5. Методи на случайното търсене 6. Симплексен метод за оптимизация 7. Предимства, недостатъци и област на приложение на без градиентните методи
 Обща постановка на задачите на нелинейното програмиране без ограничения Целева функция Допустима област
Обща постановка на задачите на нелинейното програмиране без ограничения Целева функция Допустима област
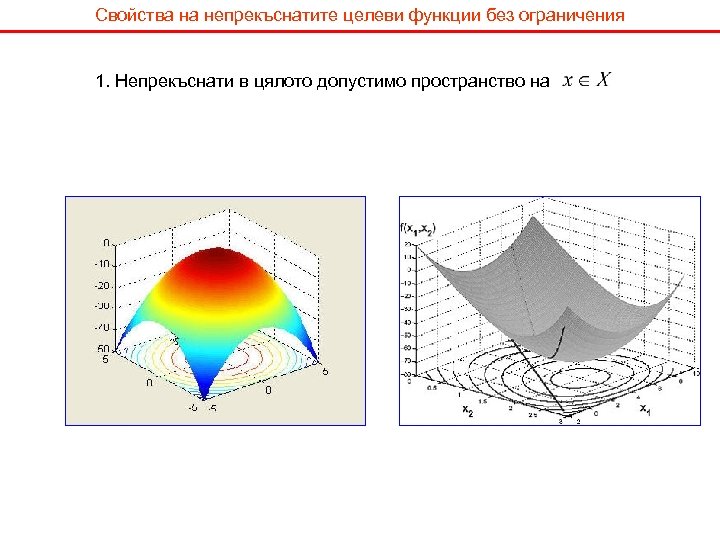 Свойства на непрекъснатите целеви функции без ограничения 1. Непрекъснати в цялото допустимо пространство на
Свойства на непрекъснатите целеви функции без ограничения 1. Непрекъснати в цялото допустимо пространство на
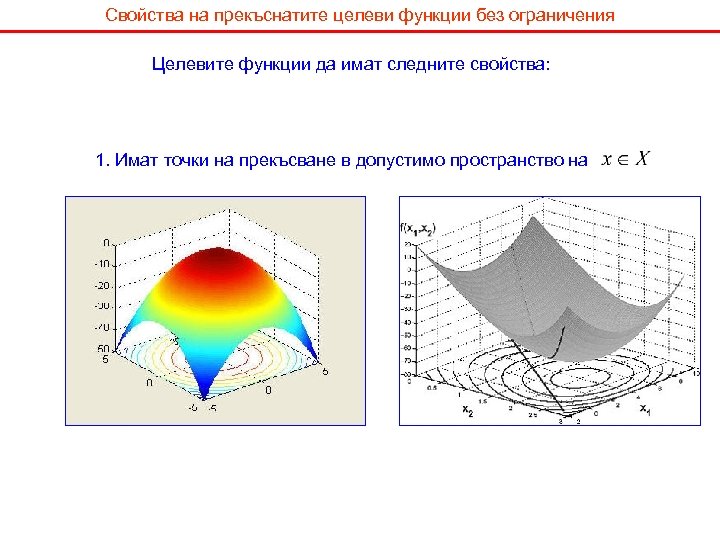 Свойства на прекъснатите целеви функции без ограничения Целевите функции да имат следните свойства: 1. Имат точки на прекъсване в допустимо пространство на
Свойства на прекъснатите целеви функции без ограничения Целевите функции да имат следните свойства: 1. Имат точки на прекъсване в допустимо пространство на
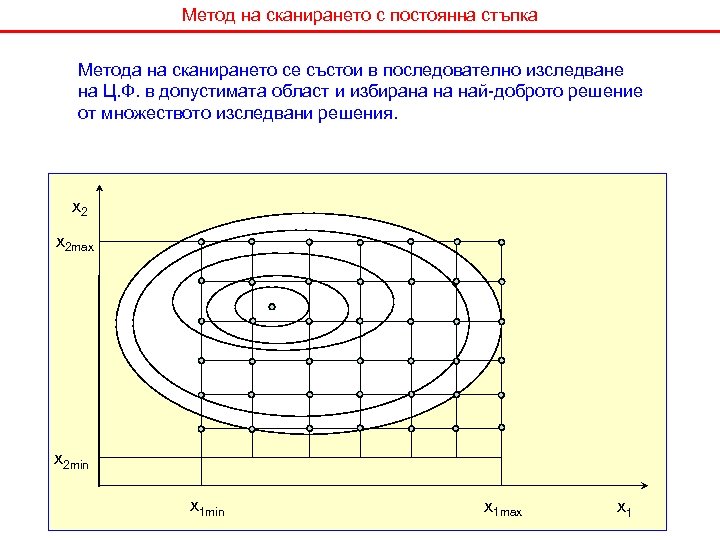 Метод на сканирането с постоянна стъпка Метода на сканирането се състои в последователно изследване на Ц. Ф. в допустимата област и избирана на най-доброто решение от множеството изследвани решения. x 2 max x 2 min x 1 max x 1
Метод на сканирането с постоянна стъпка Метода на сканирането се състои в последователно изследване на Ц. Ф. в допустимата област и избирана на най-доброто решение от множеството изследвани решения. x 2 max x 2 min x 1 max x 1
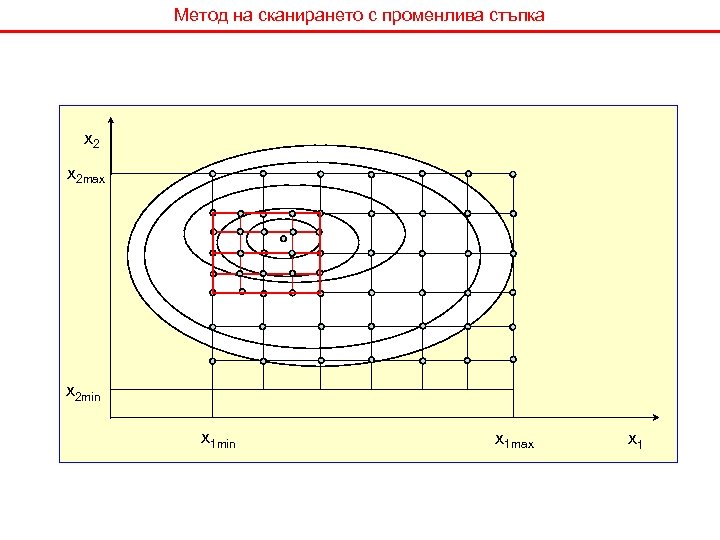 Метод на сканирането с променлива стъпка x 2 max x 2 min x 1 max x 1
Метод на сканирането с променлива стъпка x 2 max x 2 min x 1 max x 1
 Метод на сканирането с постоянна стъпка - предимства и недостатъци Предимства на метода 1. При малка стъпка дава възможност за намиране на глобален екстремум 2. Лесно се алгоритмизира 3. При две променливи могат да се построят линиите на постоянни стойност на целевата функция Недостатъци на метода 1. Необходим е голям брой на изчисления на целевата функция 2. Не е приложим при задачи с много променливи
Метод на сканирането с постоянна стъпка - предимства и недостатъци Предимства на метода 1. При малка стъпка дава възможност за намиране на глобален екстремум 2. Лесно се алгоритмизира 3. При две променливи могат да се построят линиите на постоянни стойност на целевата функция Недостатъци на метода 1. Необходим е голям брой на изчисления на целевата функция 2. Не е приложим при задачи с много променливи
 Метод на Гаус-Зайдел Методът на Гаус-Зайдел е метод на многократно изменение на управляващите параметри. Алгоритъма на метода е следния: 1. Избира се определен ред на управляващите параметри 2. Локализира се екстремума по първия управляващ параметър 3. Намерената стойност се приема за постоянна и се прави локализация по следващия параметър 4. Тази процедура се повтаря до последния управляващ параметър, след което отново започва с първия 5. Критерият за спиране на търсенето е достигането на такава точност от която при изменение с по всеки управляващ параметър не може да се намери по-добър резултат
Метод на Гаус-Зайдел Методът на Гаус-Зайдел е метод на многократно изменение на управляващите параметри. Алгоритъма на метода е следния: 1. Избира се определен ред на управляващите параметри 2. Локализира се екстремума по първия управляващ параметър 3. Намерената стойност се приема за постоянна и се прави локализация по следващия параметър 4. Тази процедура се повтаря до последния управляващ параметър, след което отново започва с първия 5. Критерият за спиране на търсенето е достигането на такава точност от която при изменение с по всеки управляващ параметър не може да се намери по-добър резултат
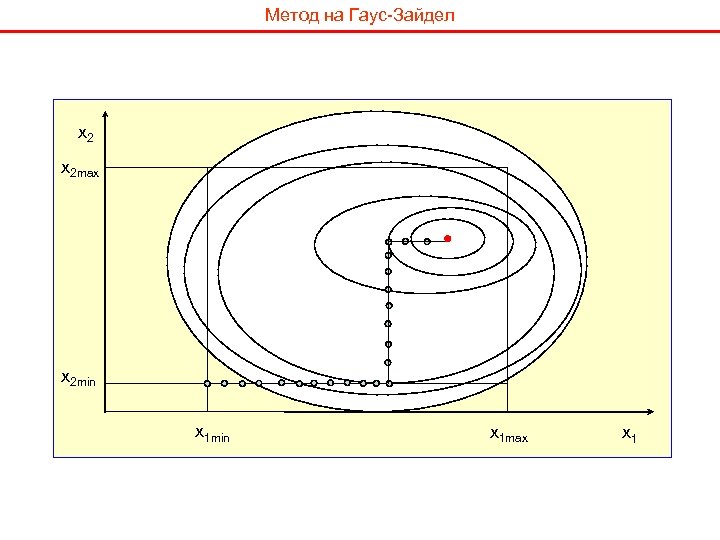 Метод на Гаус-Зайдел x 2 max x 2 min x 1 max x 1
Метод на Гаус-Зайдел x 2 max x 2 min x 1 max x 1
 Метод на простото случайно търсене Алгоритъма на метода на простото случайно търсене е следния: 1. Генерират се последователно случайни точки в допустимото пространство по формулата: N равномерно разпределени числа в границите [0, +1] 2. Във всяка точка се изчислява целевата функция 3. Сравнява се текущия екстремум до този момент. Ако. . последната точка е по-добра то тя се запомня за най-добра до този момент и генерирането на нова точка продължава. 4. Търсенето се прекратява при: a. Достигане на предварително зададен брой изчисления b. Достигане на определен брой изчисления след които не се. . е получило подобрение на текущия максимум
Метод на простото случайно търсене Алгоритъма на метода на простото случайно търсене е следния: 1. Генерират се последователно случайни точки в допустимото пространство по формулата: N равномерно разпределени числа в границите [0, +1] 2. Във всяка точка се изчислява целевата функция 3. Сравнява се текущия екстремум до този момент. Ако. . последната точка е по-добра то тя се запомня за най-добра до този момент и генерирането на нова точка продължава. 4. Търсенето се прекратява при: a. Достигане на предварително зададен брой изчисления b. Достигане на определен брой изчисления след които не се. . е получило подобрение на текущия максимум
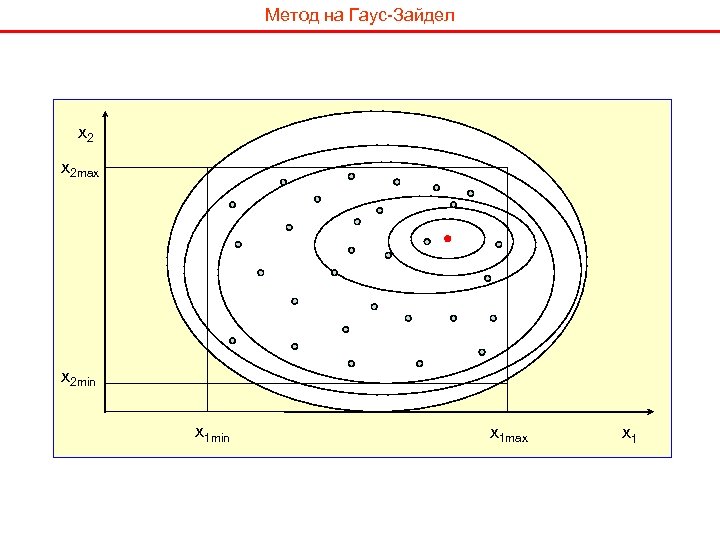 Метод на Гаус-Зайдел x 2 max x 2 min x 1 max x 1
Метод на Гаус-Зайдел x 2 max x 2 min x 1 max x 1
 Метод на случайното търсене с увеличена плътност Алгоритъма на метода е следния: 1. Генерират се първа случайна точка в допустимото пространство по формулата: 2. Изчислява се Ц. Ф. И се приема получената стойност за текущ екстремум 3. Следващите случайни точки се определят по формулата: 4. Ако новата точка нарушава допустимото пространство, тя се връща на нарушената граница. 5. Изчислява се Ц. Ф. в новата точка 6. Ако проверява се дали е изпълнен критерия за спиране на търсенето, т. е. Ако има M неудачни изчисления без подобрение на Ц. Ф. 7. Ако приема се и алгоритъма се повтаря в т. 3 Запомня се
Метод на случайното търсене с увеличена плътност Алгоритъма на метода е следния: 1. Генерират се първа случайна точка в допустимото пространство по формулата: 2. Изчислява се Ц. Ф. И се приема получената стойност за текущ екстремум 3. Следващите случайни точки се определят по формулата: 4. Ако новата точка нарушава допустимото пространство, тя се връща на нарушената граница. 5. Изчислява се Ц. Ф. в новата точка 6. Ако проверява се дали е изпълнен критерия за спиране на търсенето, т. е. Ако има M неудачни изчисления без подобрение на Ц. Ф. 7. Ако приема се и алгоритъма се повтаря в т. 3 Запомня се
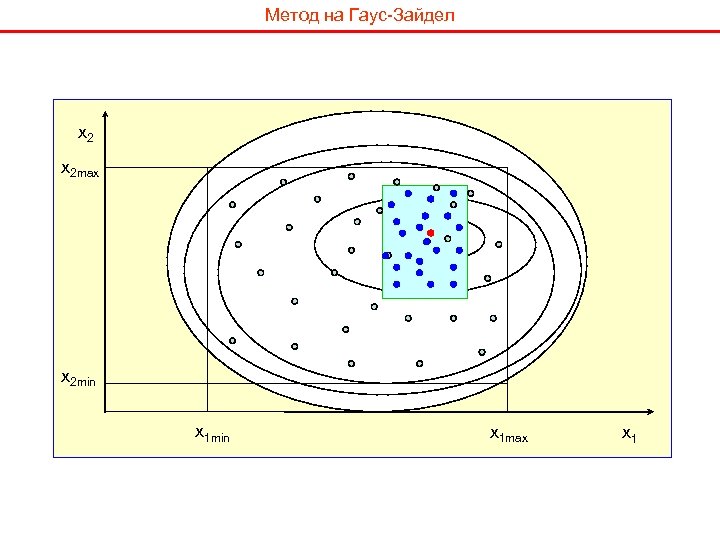 Метод на Гаус-Зайдел x 2 max x 2 min x 1 max x 1
Метод на Гаус-Зайдел x 2 max x 2 min x 1 max x 1
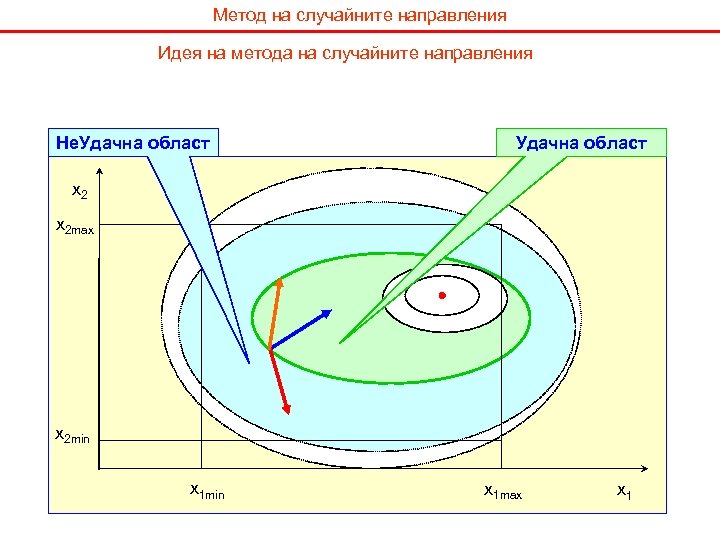 Метод на случайните направления Идея на метода на случайните направления Не. Удачна област x 2 max x 2 min x 1 max x 1
Метод на случайните направления Идея на метода на случайните направления Не. Удачна област x 2 max x 2 min x 1 max x 1
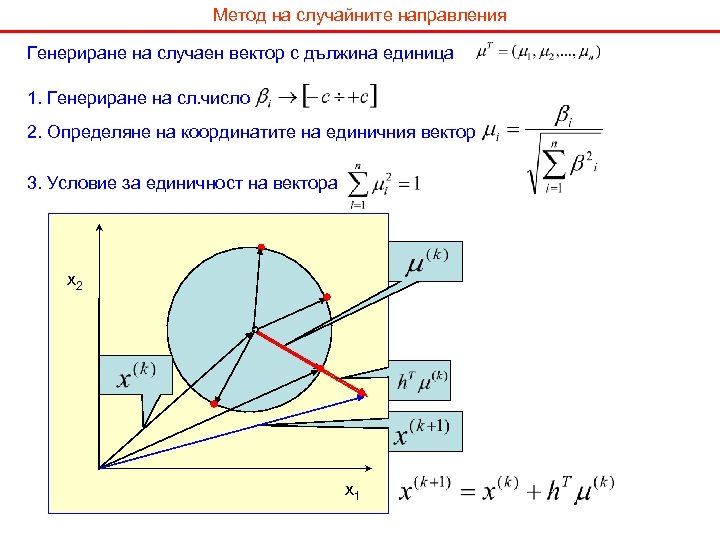 Метод на случайните направления Генериране на случаен вектор с дължина единица 1. Генериране на сл. число 2. Определяне на координатите на единичния вектор 3. Условие за единичност на вектора x 2 x 1
Метод на случайните направления Генериране на случаен вектор с дължина единица 1. Генериране на сл. число 2. Определяне на координатите на единичния вектор 3. Условие за единичност на вектора x 2 x 1
 Метод на случайните направления Алгоритъм на метода на случайните направления 1. Задава се начална стартова точка в допустимата област 2. Генерира се случаен вектор с дължина единица 3. Формира се вектора за (k+1) –та стъпка, чрез векторната сума 4. Проверява се дали полученият вектор е в удачно направление MAXIMUM MINIMUM 5. При вектор в неудачно направление се генерира нов единичен вектор 6. Проверява се дали е изпълнен критерия за спиране на търсенето 7. Ако критерия е изпълнен то полученото най добро решение се приема за окончателно, ако не процедурата се повтаря в т. 3
Метод на случайните направления Алгоритъм на метода на случайните направления 1. Задава се начална стартова точка в допустимата област 2. Генерира се случаен вектор с дължина единица 3. Формира се вектора за (k+1) –та стъпка, чрез векторната сума 4. Проверява се дали полученият вектор е в удачно направление MAXIMUM MINIMUM 5. При вектор в неудачно направление се генерира нов единичен вектор 6. Проверява се дали е изпълнен критерия за спиране на търсенето 7. Ако критерия е изпълнен то полученото най добро решение се приема за окончателно, ако не процедурата се повтаря в т. 3
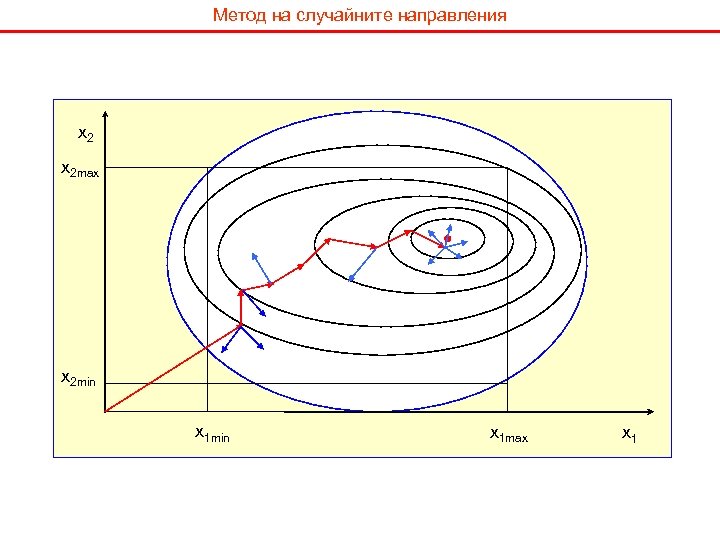 Метод на случайните направления x 2 max x 2 min x 1 max x 1
Метод на случайните направления x 2 max x 2 min x 1 max x 1
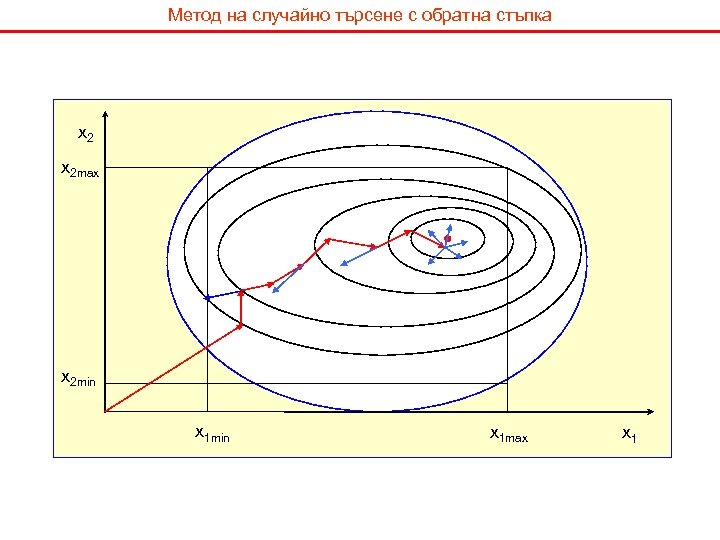 Метод на случайно търсене с обратна стъпка x 2 max x 2 min x 1 max x 1
Метод на случайно търсене с обратна стъпка x 2 max x 2 min x 1 max x 1
 Симплексен метод за оптимизация Метод за едновременно изучаване на Ц. Ф. И за движение към екстремума въз основа на изчисления на Ц. Ф. В точки образуващи симплекс в пространството. Симплекс в многомерното пространство 1. Симплекс в нуламерното пространство - точка 2. Симплекс в едномерното пространство – права линия 3. Симплекс в двумерното пространство – триъгълник 4. Симплекс в тримерното пространство – пирамида
Симплексен метод за оптимизация Метод за едновременно изучаване на Ц. Ф. И за движение към екстремума въз основа на изчисления на Ц. Ф. В точки образуващи симплекс в пространството. Симплекс в многомерното пространство 1. Симплекс в нуламерното пространство - точка 2. Симплекс в едномерното пространство – права линия 3. Симплекс в двумерното пространство – триъгълник 4. Симплекс в тримерното пространство – пирамида
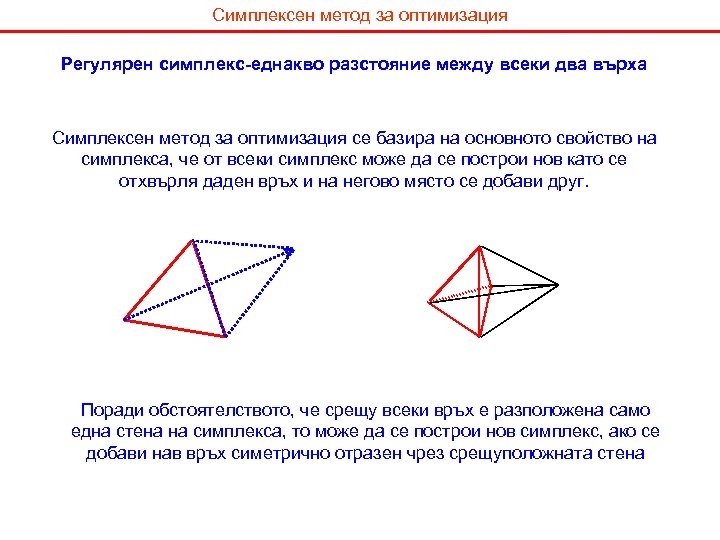 Симплексен метод за оптимизация Регулярен симплекс-еднакво разстояние между всеки два върха Симплексен метод за оптимизация се базира на основното свойство на симплекса, че от всеки симплекс може да се построи нов като се отхвърля даден връх и на негово място се добави друг. Поради обстоятелството, че срещу всеки връх е разположена само една стена на симплекса, то може да се построи нов симплекс, ако се добави нав връх симетрично отразен чрез срещуположната стена
Симплексен метод за оптимизация Регулярен симплекс-еднакво разстояние между всеки два върха Симплексен метод за оптимизация се базира на основното свойство на симплекса, че от всеки симплекс може да се построи нов като се отхвърля даден връх и на негово място се добави друг. Поради обстоятелството, че срещу всеки връх е разположена само една стена на симплекса, то може да се построи нов симплекс, ако се добави нав връх симетрично отразен чрез срещуположната стена
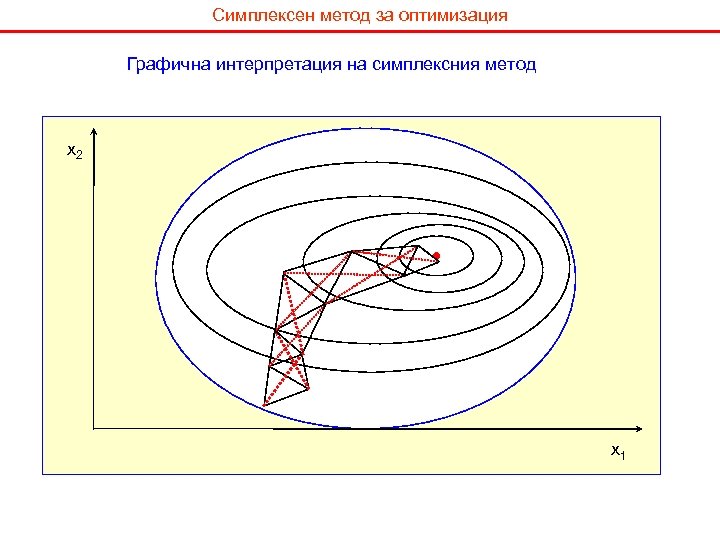 Симплексен метод за оптимизация Графична интерпретация на симплексния метод x 2 x 1
Симплексен метод за оптимизация Графична интерпретация на симплексния метод x 2 x 1
 Симплексен метод за оптимизация Алгоритъм на симплексния метод 1. Избира се стартова точка около която се формира начален симплекс 2. Задават се условни размери на началния симплекс 3. Около началната точка се формира началния симплекс със зададените условни размери 4. Изчислява се Ц. Ф. За всеки връх на симплекса 5. Определя се върха с най лош резултат 6. Изчисляват се координатите на нов връх симетрично отразен от върха с най лош резултат 7. Новополученият връх се приема за връх на симплекса на мястото на отразения 8. Изчислява се Ц. Ф. В новия връх на симплекса 9. Алгоритъма се повтаря в т. 5 10. Критерия за спиране на търсенето е зацикляне на симплекса около един връх с най-добър резултат за Ц. Ф. 11. След зацикляне на симплекса, около точката с най-добър резултат се формира нав симплекс с намалени размери и търсенето продължава в т. 4
Симплексен метод за оптимизация Алгоритъм на симплексния метод 1. Избира се стартова точка около която се формира начален симплекс 2. Задават се условни размери на началния симплекс 3. Около началната точка се формира началния симплекс със зададените условни размери 4. Изчислява се Ц. Ф. За всеки връх на симплекса 5. Определя се върха с най лош резултат 6. Изчисляват се координатите на нов връх симетрично отразен от върха с най лош резултат 7. Новополученият връх се приема за връх на симплекса на мястото на отразения 8. Изчислява се Ц. Ф. В новия връх на симплекса 9. Алгоритъма се повтаря в т. 5 10. Критерия за спиране на търсенето е зацикляне на симплекса около един връх с най-добър резултат за Ц. Ф. 11. След зацикляне на симплекса, около точката с най-добър резултат се формира нав симплекс с намалени размери и търсенето продължава в т. 4
 Симплексен метод за оптимизация Предимства на симплексния метод 1. Методът е много ефективен при голям брой управляващи променливи 2. Методът е приложим и за числена, и за експериментална оптимизация 3. Методът може да се усъвършенства като размерите на симплекса се изменят в зависимост от получените резултати (Метод на Нелдер-Мид) Недостатъци на симплексния метод 1. Силна зависимост на сходимостта от удачния избор на ориентацията на началния симплекс 2. Трудност при опериране с матрицата с координатите на върховете при голям брой променливи
Симплексен метод за оптимизация Предимства на симплексния метод 1. Методът е много ефективен при голям брой управляващи променливи 2. Методът е приложим и за числена, и за експериментална оптимизация 3. Методът може да се усъвършенства като размерите на симплекса се изменят в зависимост от получените резултати (Метод на Нелдер-Мид) Недостатъци на симплексния метод 1. Силна зависимост на сходимостта от удачния избор на ориентацията на началния симплекс 2. Трудност при опериране с матрицата с координатите на върховете при голям брой променливи


