Приложно математично програмиране ЛЕКЦИЯ 4 Нелинейно програмиране —

Приложно математично програмиране ЛЕКЦИЯ 4 Нелинейно програмиране - Градиентни методи Prof. Boyan Bonev Ivanov, Ph. D. Email: bivanov@bas. bg Institute of Chemical Engineering-BAS

Лекции Лекция 1 Въведение в математичното програмиране Лекция 2 Линейно програмиране Лекция 3 Оптимизация при целеви функции с един управляващ параметър Лекция 4 Нелинейно програмиране – Градиентни методи Лекция 5 Нелинейно програмиране – Директни методи Лекция 6 Нелинейно програмиране – Методи с ограничения Лекция 7 Методи за булева и дискретна оптимизация Лекция 8 Методи за глобална оптимизация Лекция 9 Методи за многоцелева оптимизация 2

План на лекцията 1. Обща постановка на задачите на нелинейното програмиране без ограничения 2. Свойства на непрекъснатите целеви функции без ограничения 3. Условия за съществуване на екстремум на целеви функции без ограничения 4. Общ принцип на градиентните методи за търсене на екстремум 5. Градиентни методи от I-ви порядък 6. Градиентни методи от II-ри порядък 7. Предимства, недостатъци и област на приложение на градиентните методи

Обща постановка на задачите на нелинейното програмиране без ограничения Целева функция Допустими области Задача без ограничения

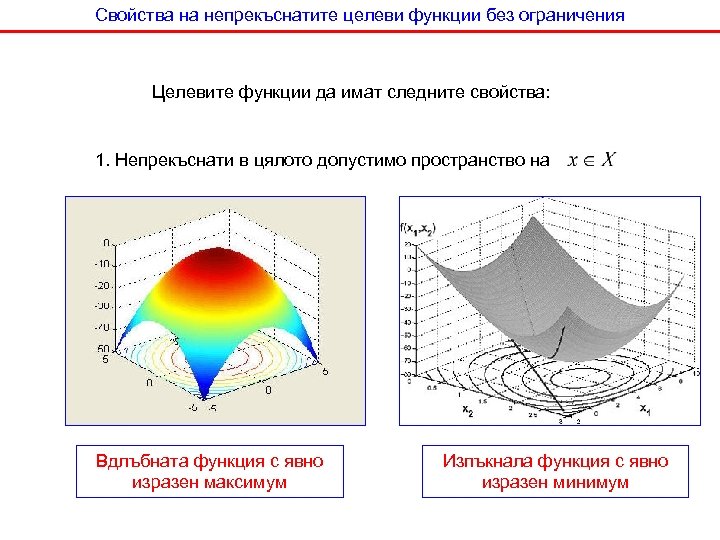Свойства на непрекъснатите целеви функции без ограничения Целевите функции да имат следните свойства: 1. Непрекъснати в цялото допустимо пространство на Вдлъбната функция с явно изразен максимум Изпъкнала функция с явно изразен минимум

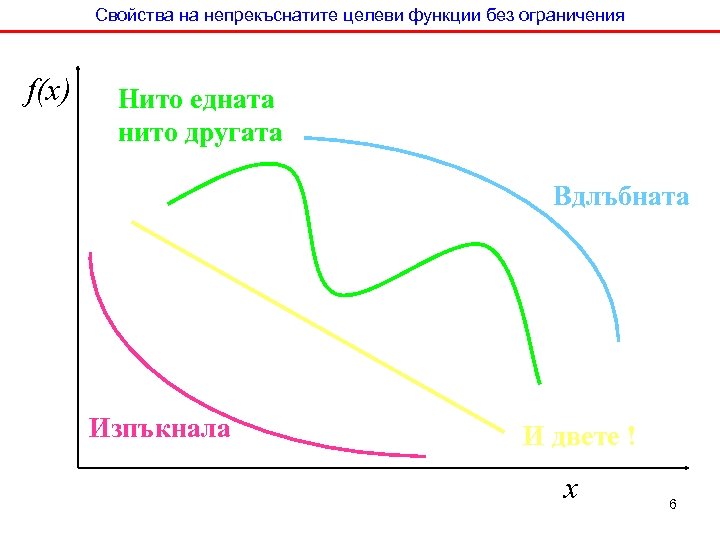Свойства на непрекъснатите целеви функции без ограничения f(x) Нито едната нито другата Вдлъбната Изпъкнала И двете ! x 6

Условия за съществуване на екстремум на целеви функции без ограничения

Общ принцип на градиентните методи за търсене на екстремум 1. Градиентните алгоритми за търсене на екстремум се базират на линейната или квадратичната апроксимация на целевата функция 2. Линейната апроксимация от първи ред на функцията може да се представи като част от разложението в ред на Тейлор 3. Квадратичната апроксимация на функцията може да се представи като част от разложението в ред на Тейлор, като се отхвърлят членовете от трети и по-висок ред

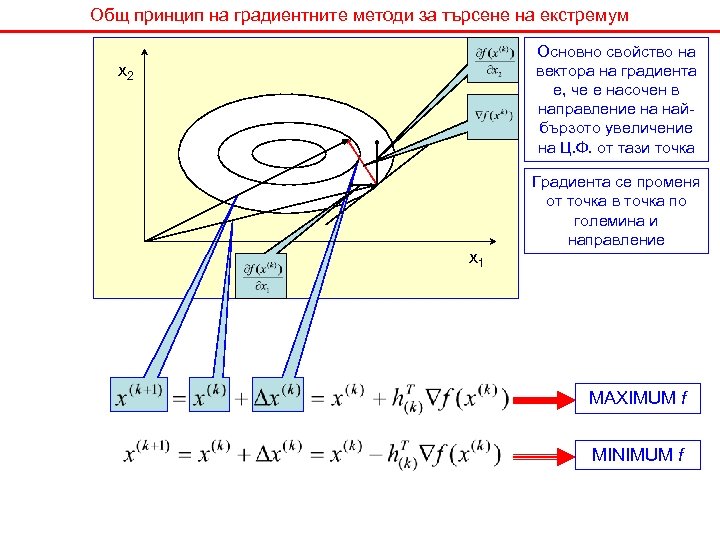Общ принцип на градиентните методи за търсене на екстремум Основно свойство на вектора на градиента е, че е насочен в направление на найбързото увеличение на Ц. Ф. от тази точка x 2 x 1 Градиента се променя от точка в точка по големина и направление MAXIMUM f MINIMUM f

Общ принцип на градиентните методи за търсене на екстремум Основен алгоритъм за търсене на екстремум на Ц. Ф. 1. Определя се стартова точка за начало на търсенето 2. Определя се вектора на градиента в стартовата точка 3. Изчисляват се координатите на следващата точка с използуване на векторната сума MAXIMUM f MINIMUM f 4. Определя се вектора на градиента в новата точка 5. Изчисляват се координатите на новата точка 6. Проверява се дали е изпълнен критерия за спиране на търсенето 6. При изпълнение на критерия за спиране търсенето приключва, а в противен случай се изпълняват стъпките от т. 3

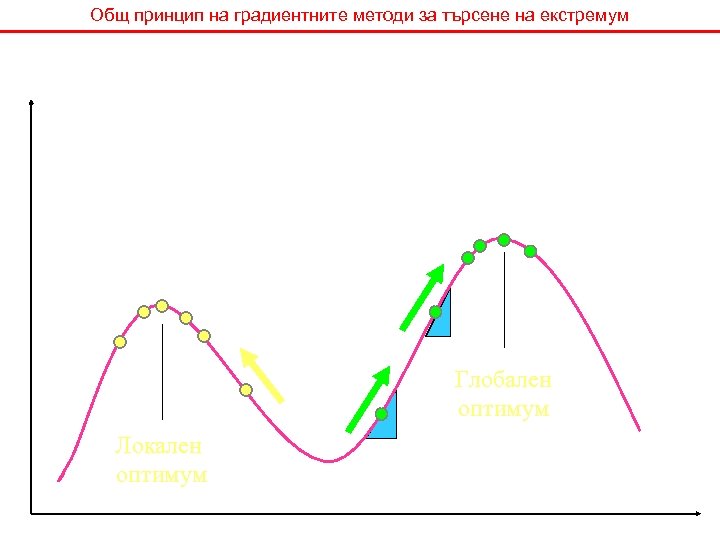Общ принцип на градиентните методи за търсене на екстремум Глобален оптимум Локален оптимум

Градиентни методи от I-ви порядък- Метод на най-бързото изкачване Алгоритъм на метод на най-бързото изкачване 1. В дадена начална точка се оценява градиента на целевата функция 2. Проверява се критерия за спиране на търсенето 3. В градиентно направление се правят стъпки до точката, в която Ц. Ф. се подобрява без да се оценява градиента MAXIMUM f MINIMUM f 4. След локализация на екстремума в първоначалното градиентно направление получената точка се приема за начална и търсенето продължава от т. 1.

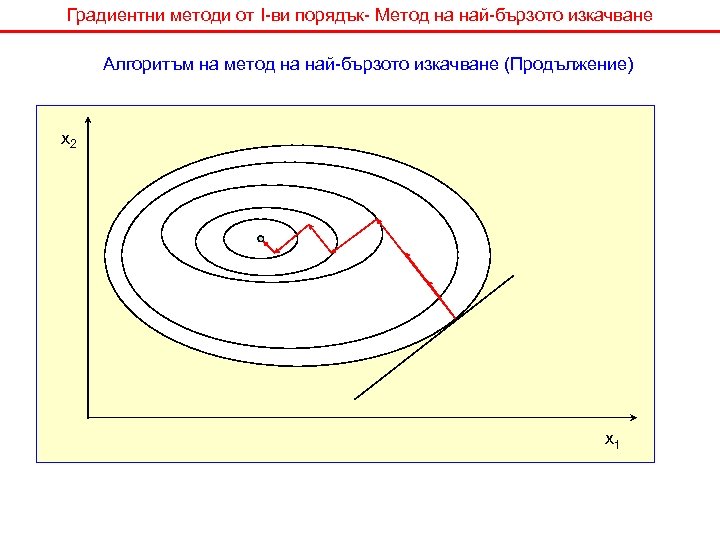Градиентни методи от I-ви порядък- Метод на най-бързото изкачване Алгоритъм на метод на най-бързото изкачване (Продължение) x 2 x 1

Градиентни методи от I-ви порядък-Метод на релаксацията Алгоритъм на метод на релаксацията 1. В дадена начална точка се оценява градиента на целевата функция и се проверява критерия за спиране на търсенето 2. Избира се управляващ параметър по който Ц. Ф. се изменя най-бързо 3. Всички параметри с изключение на xr се приемат равни на началните им стойности 4. Локализира се MAX по xr 5. След локализацията на екстремума по дадения параметър, новата точка се приема за начална и алгоритъма се повтаря в т. 2.

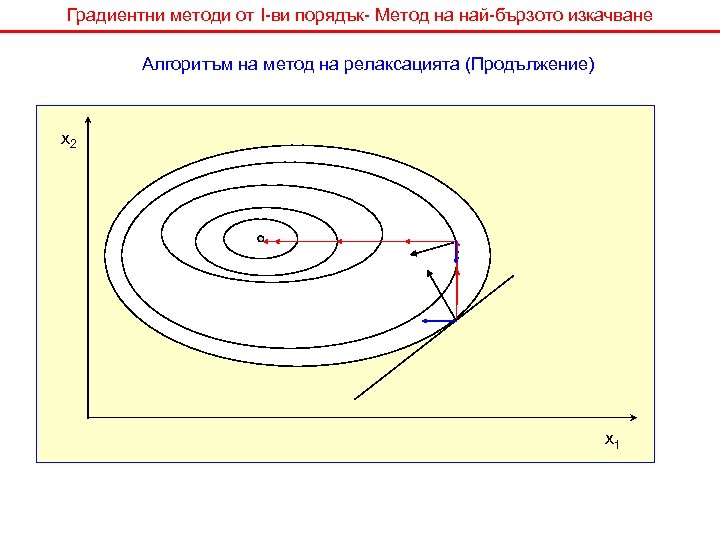Градиентни методи от I-ви порядък- Метод на най-бързото изкачване Алгоритъм на метод на релаксацията (Продължение) x 2 x 1

Градиентни методи от II-ри порядък Метод на Нютон-Рафсън, използуващ втори производни на Ц. Ф. Метода се базира на квадратичната апроксимация на Ц. Ф. MAX на Ц. Ф. В направление на се определя от условието:

Градиентни методи от II-ри порядък Метод на Нютон-Рафсън, използуващ втори производни на Ц. Ф. 1. Направлението към екстремума и големината на стъпката са точно дефинирани при положително определена матрица на Хес. 2. При квадратична функция за намиране на екстремума е необходима една стъпка, но за произволна функция екстремума се достига итеративно. 3. При всяка итерация е необходимо да се обръща матрицата на Хес и аналитично изчисляване на вторите частни производни. 4. Сходимостта на метода се гарантира само ако функцията е два пъти диференцируема и обратната матрица на Хес е положителна 5. Метода на Нютон е добре да се използува като завършваща процедура, като в началото се използува подхода на най-бързото спускане.

Градиентни методи от II-ри порядък Предимства и недостатъци на градиентните методи Предимства на градиентните методи 1. Бърза сходимост при аналитично зададени производни 2. Бърза сходимост при квадратични или близки до тях функции Недостатъци на градиентните методи 1. Градиентните методи дават възможност за локализация на най-близкия локален екстремум 3. Трудно се избират параметрите за численото диференциране 2. Възможно е засядане в седловидна точка 4. Посоката на движение към екстремума и скоростта на сходимост зависят от дименсиите и големината на параметъра на стъпката 5. При много управляващи променливи се изисква голям брой изчисления на целевата функция