e63a3b37c97286462bc87352bf70203a.ppt
- Количество слайдов: 63
 Приложно математично програмиране ЛЕКЦИЯ 2 Линейно програмиране Prof. Boyan Bonev Ivanov, Ph. D. Email: bivanov@bas. bg Institute of Chemical Engineering-BAS
Приложно математично програмиране ЛЕКЦИЯ 2 Линейно програмиране Prof. Boyan Bonev Ivanov, Ph. D. Email: bivanov@bas. bg Institute of Chemical Engineering-BAS
 Лекции Лекция 1 Въведение в математичното програмиране Лекция 2 Линейно програмиране Лекция 3 Оптимизация при целеви функции с един управляващ параметър Лекция 4 Нелинейно програмиране – Градиентни методи Лекция 5 Нелинейно програмиране – Директни методи Лекция 6 Нелинейно програмиране – Методи с ограничения Лекция 7 Методи за булева и дискретна оптимизация Лекция 8 Методи за глобална оптимизация Лекция 9 Методи за многоцелева оптимизация
Лекции Лекция 1 Въведение в математичното програмиране Лекция 2 Линейно програмиране Лекция 3 Оптимизация при целеви функции с един управляващ параметър Лекция 4 Нелинейно програмиране – Градиентни методи Лекция 5 Нелинейно програмиране – Директни методи Лекция 6 Нелинейно програмиране – Методи с ограничения Лекция 7 Методи за булева и дискретна оптимизация Лекция 8 Методи за глобална оптимизация Лекция 9 Методи за многоцелева оптимизация
 Въведение в линейното програмиране
Въведение в линейното програмиране
 План на лекцията • История на линейното програмиране • Примери за задачи от линейното програмиране • Графическа интерпретация на задачи от линейното програмиране • Стандартна форма на записване • Основни понятия използувани в линейното програмиране 4
План на лекцията • История на линейното програмиране • Примери за задачи от линейното програмиране • Графическа интерпретация на задачи от линейното програмиране • Стандартна форма на записване • Основни понятия използувани в линейното програмиране 4
 Основоположник на линейното програмиране • George Dantzig – Junior Statistician U. S. Bureau of Labor Statistics (1937 -39) – Head of USAF Combat Analysis Branch (1941 -46) – Ph. D Mathematics, Cal Berkeley (1946) – Invented “Simplex” method for solving linear programs (1947) 5
Основоположник на линейното програмиране • George Dantzig – Junior Statistician U. S. Bureau of Labor Statistics (1937 -39) – Head of USAF Combat Analysis Branch (1941 -46) – Ph. D Mathematics, Cal Berkeley (1946) – Invented “Simplex” method for solving linear programs (1947) 5
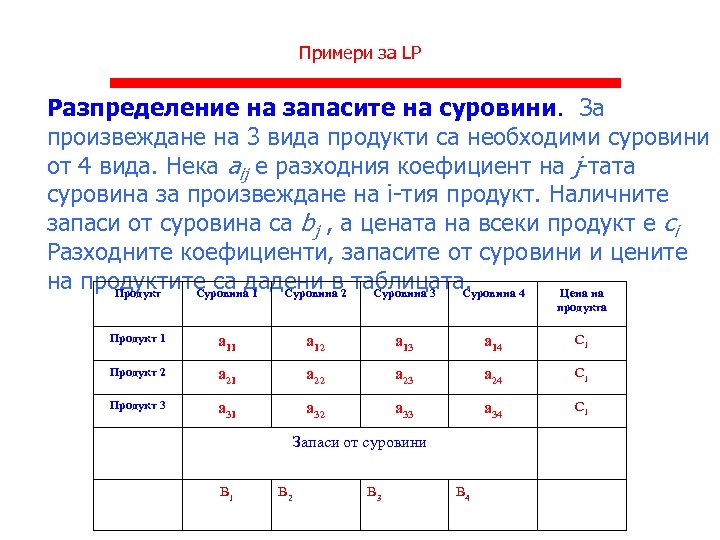 Примери за LP Разпределение на запасите на суровини. За произвеждане на 3 вида продукти са необходими суровини от 4 вида. Нека aij е разходния коефициент на j-тата суровина за произвеждане на i-тия продукт. Наличните запаси от суровина са bj , а цената на всеки продукт е ci Разходните коефициенти, запасите от суровини и цените на продуктите са дадени в таблицата. Продукт Суровина 1 Суровина 2 Суровина 3 Суровина 4 Цена на продукта Продукт 1 a 12 a 13 a 14 С 1 Продукт 2 a 21 a 22 a 23 a 24 С 1 Продукт 3 a 31 a 32 a 33 a 34 С 1 Запаси от суровини B 1 B 2 B 3 B 4
Примери за LP Разпределение на запасите на суровини. За произвеждане на 3 вида продукти са необходими суровини от 4 вида. Нека aij е разходния коефициент на j-тата суровина за произвеждане на i-тия продукт. Наличните запаси от суровина са bj , а цената на всеки продукт е ci Разходните коефициенти, запасите от суровини и цените на продуктите са дадени в таблицата. Продукт Суровина 1 Суровина 2 Суровина 3 Суровина 4 Цена на продукта Продукт 1 a 12 a 13 a 14 С 1 Продукт 2 a 21 a 22 a 23 a 24 С 1 Продукт 3 a 31 a 32 a 33 a 34 С 1 Запаси от суровини B 1 B 2 B 3 B 4
 Примери за LP Задачата е да се определи колко продукт от трите вида може да се произведе при наличните запаси от суровини, така че да се получи максимална печалба.
Примери за LP Задачата е да се определи колко продукт от трите вида може да се произведе при наличните запаси от суровини, така че да се получи максимална печалба.
 Примери за LP Задача за съставяне на оптимални смеси. Разполага се с n вида продукти за хранене xi (i=1, …n) съответно с цени ci (i=1, …n). Задачата е да се състави оптимална хранителна смес с минимална цена. Хранителната смес трябва да отговаря на определени изисквания за съставките (белтъчни, въглехидрати, мазнини и др. ) bj (j=1, …m). Нека съдържанието на jтата съставка в i-тия продукт е aij. Задачата е да се определят количествата от отделните продукти така, че цената на получената смес да бъде минимална.
Примери за LP Задача за съставяне на оптимални смеси. Разполага се с n вида продукти за хранене xi (i=1, …n) съответно с цени ci (i=1, …n). Задачата е да се състави оптимална хранителна смес с минимална цена. Хранителната смес трябва да отговаря на определени изисквания за съставките (белтъчни, въглехидрати, мазнини и др. ) bj (j=1, …m). Нека съдържанието на jтата съставка в i-тия продукт е aij. Задачата е да се определят количествата от отделните продукти така, че цената на получената смес да бъде минимална.
 LP Стандартна форма Max Z = c 1 x 1 + c 2 x 2 + … + cnxn Subject to (s. t. ) a 11 x 1 + a 12 x 2 + … + a 1 nxn b 1 a 21 x 1 + a 22 x 2 + … + a 2 nxn b 2 … am 1 x 1 + am 2 x 2 + … + amnxn bm x 1 0, x 2 0, …, xn 0 9
LP Стандартна форма Max Z = c 1 x 1 + c 2 x 2 + … + cnxn Subject to (s. t. ) a 11 x 1 + a 12 x 2 + … + a 1 nxn b 1 a 21 x 1 + a 22 x 2 + … + a 2 nxn b 2 … am 1 x 1 + am 2 x 2 + … + amnxn bm x 1 0, x 2 0, …, xn 0 9
 LP Стандартна форма n Max Z = cj xj j =1 Subject to (s. t. ) n aij xj bj j =1 i = 1, … , m xj 0 j = 1, … , m 10
LP Стандартна форма n Max Z = cj xj j =1 Subject to (s. t. ) n aij xj bj j =1 i = 1, … , m xj 0 j = 1, … , m 10
 Основни положения от LP • Линейна целева функция, ограничения – Пропорционалност – Адитивност • Делимост – Непрекъснатост на променливите • Сигурност – Определени параметри 11
Основни положения от LP • Линейна целева функция, ограничения – Пропорционалност – Адитивност • Делимост – Непрекъснатост на променливите • Сигурност – Определени параметри 11
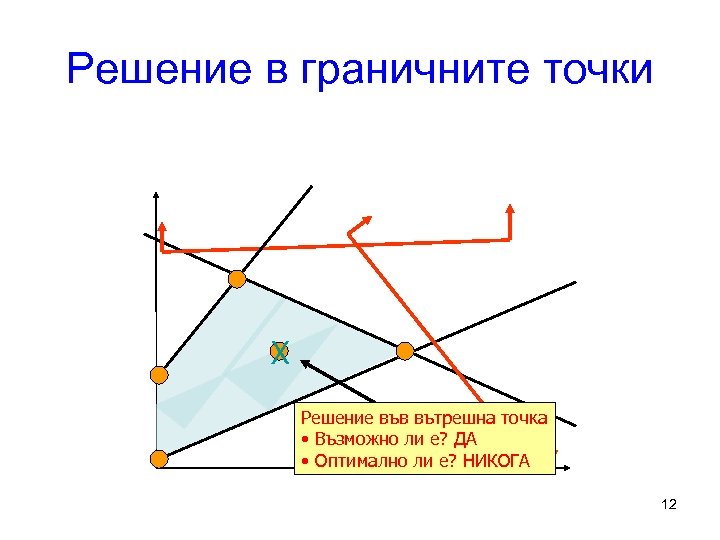 Решение в граничните точки X Решение във вътрешна точка • Възможно ли е? ДА • Оптимално ли е? НИКОГА 12
Решение в граничните точки X Решение във вътрешна точка • Възможно ли е? ДА • Оптимално ли е? НИКОГА 12
 LP Специални случаи • Алтернативни оптимуми • Невъзможни проблеми • Безкрайни проблеми 13
LP Специални случаи • Алтернативни оптимуми • Невъзможни проблеми • Безкрайни проблеми 13
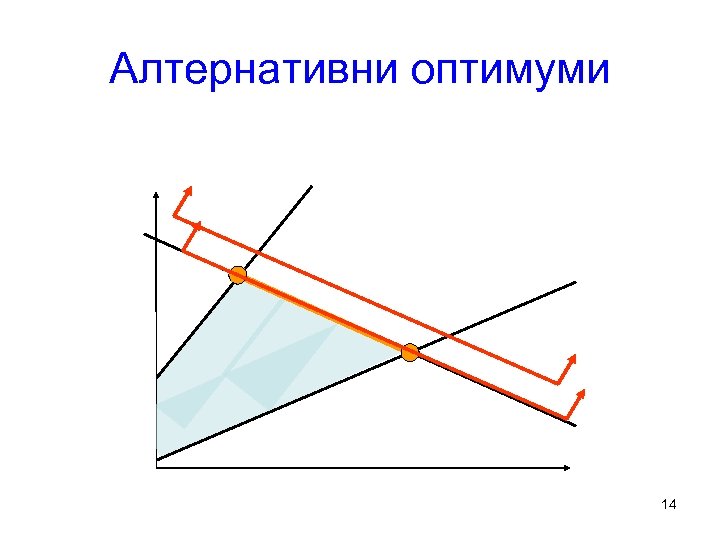 Алтернативни оптимуми 14
Алтернативни оптимуми 14
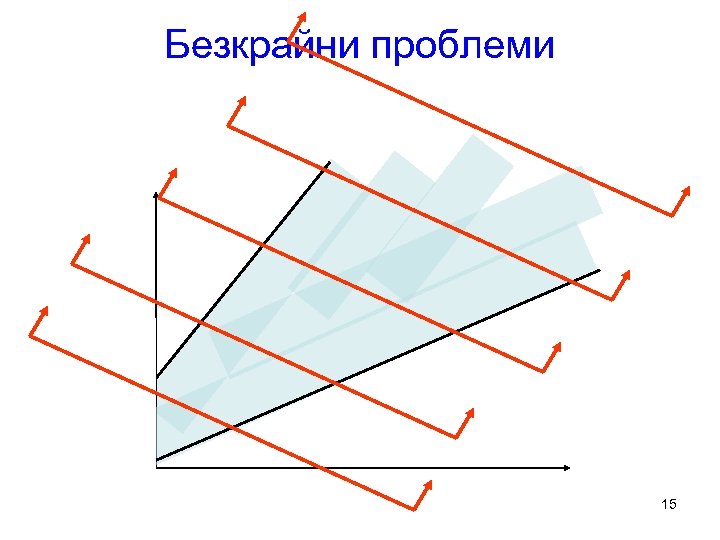 Безкрайни проблеми 15
Безкрайни проблеми 15
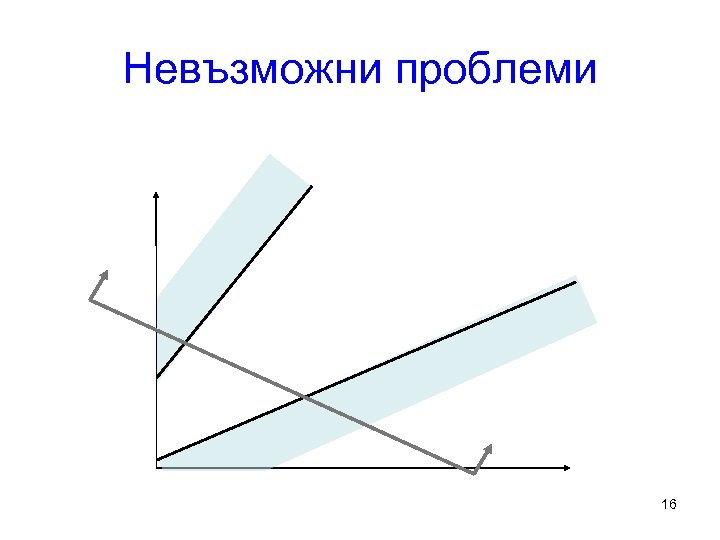 Невъзможни проблеми 16
Невъзможни проблеми 16
 LP Понятия • • Независими променливи Целева функция Ограничения Възможни решения Възможни области Гранични точки на решението Оптимално решение Оптималност на границата 17
LP Понятия • • Независими променливи Целева функция Ограничения Възможни решения Възможни области Гранични точки на решението Оптимално решение Оптималност на границата 17
 Метод на линейното програмиране
Метод на линейното програмиране
 План на лекцията • Основи на симплексния метод • Симплексен метод за решаване задачата за максимум • Теория на симплексния метод • Симплексен метод за други проблеми 19
План на лекцията • Основи на симплексния метод • Симплексен метод за решаване задачата за максимум • Теория на симплексния метод • Симплексен метод за други проблеми 19
 Пример за задача на LP Product Mix LP. A potter produces two products, a pitcher and a bowl. It takes about 1 hour to produce a bowl and requires 4 pounds of clay. A pitcher takes about 2 hours and consumes 3 pounds of clay. The profit on a bowl is $40 and $50 on a pitcher. She works 40 hours weekly, has 120 pounds of clay available each week, and wants more profits. Max Z = 40 x + 50 y s. t. 1 x + 2 y 40 4 x + 3 y 120 x, y 0 Печалба времетраене глина не отрицателност 20
Пример за задача на LP Product Mix LP. A potter produces two products, a pitcher and a bowl. It takes about 1 hour to produce a bowl and requires 4 pounds of clay. A pitcher takes about 2 hours and consumes 3 pounds of clay. The profit on a bowl is $40 and $50 on a pitcher. She works 40 hours weekly, has 120 pounds of clay available each week, and wants more profits. Max Z = 40 x + 50 y s. t. 1 x + 2 y 40 4 x + 3 y 120 x, y 0 Печалба времетраене глина не отрицателност 20
 Стандартна форма на представяне Изходна задача Max Z = 40 x 1 + 50 x 2 s. t. 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1 , x 2 - свободни управляващи променливи 21
Стандартна форма на представяне Изходна задача Max Z = 40 x 1 + 50 x 2 s. t. 1 x 1 + 2 x 2 40 4 x 1 + 3 x 2 120 x 1 , x 2 - свободни управляващи променливи 21
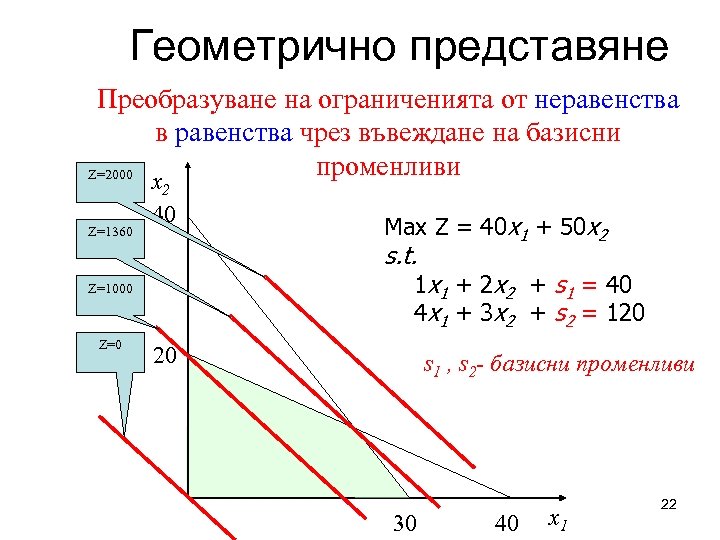 Геометрично представяне Преобразуване на ограниченията от неравенства в равенства чрез въвеждане на базисни променливи Z=2000 x 2 Z=1360 40 s. t. 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 Z=1000 Z=0 Max Z = 40 x 1 + 50 x 2 20 s 1 , s 2 - базисни променливи 30 40 x 1 22
Геометрично представяне Преобразуване на ограниченията от неравенства в равенства чрез въвеждане на базисни променливи Z=2000 x 2 Z=1360 40 s. t. 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 Z=1000 Z=0 Max Z = 40 x 1 + 50 x 2 20 s 1 , s 2 - базисни променливи 30 40 x 1 22
 Стандартна форма на представяне Решаване на уравненията на ограниченията спрямо базисните променливи Max Z = 40 x 1 + 50 x 2 s. t. s 1 = 40 -1 x 1 - 2 x 2 s 2 = 120 -4 x 1 -3 x 2 x 1 , x 2 , s 1 , s 2 0 x 1 , x 2 - свободни управляващи променливи s 1 , s 2 - базисни променливи 23
Стандартна форма на представяне Решаване на уравненията на ограниченията спрямо базисните променливи Max Z = 40 x 1 + 50 x 2 s. t. s 1 = 40 -1 x 1 - 2 x 2 s 2 = 120 -4 x 1 -3 x 2 x 1 , x 2 , s 1 , s 2 0 x 1 , x 2 - свободни управляващи променливи s 1 , s 2 - базисни променливи 23
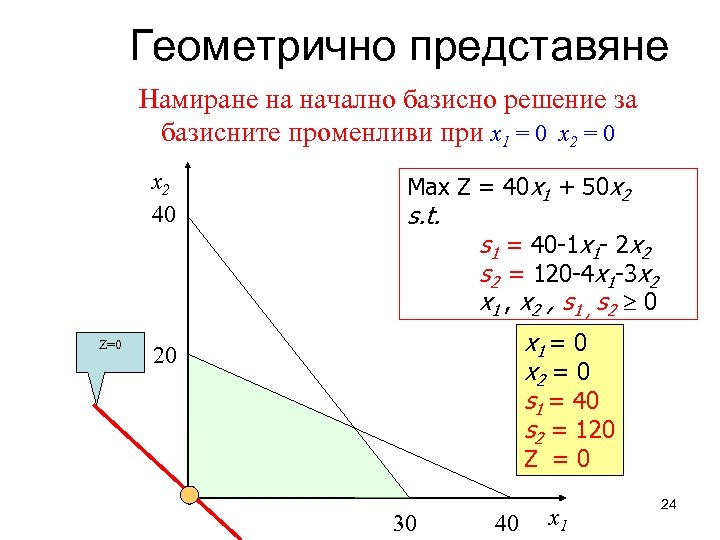 Геометрично представяне Намиране на начално базисно решение за базисните променливи при x 1 = 0 x 2 40 Z=0 Max Z = 40 x 1 + 50 x 2 s. t. s 1 = 40 -1 x 1 - 2 x 2 s 2 = 120 -4 x 1 -3 x 2 x 1 , x 2 , s 1 , s 2 0 x 1 = 0 x 2 = 0 s 1 = 40 s 2 = 120 20 Z = 0 30 40 x 1 24
Геометрично представяне Намиране на начално базисно решение за базисните променливи при x 1 = 0 x 2 40 Z=0 Max Z = 40 x 1 + 50 x 2 s. t. s 1 = 40 -1 x 1 - 2 x 2 s 2 = 120 -4 x 1 -3 x 2 x 1 , x 2 , s 1 , s 2 0 x 1 = 0 x 2 = 0 s 1 = 40 s 2 = 120 20 Z = 0 30 40 x 1 24
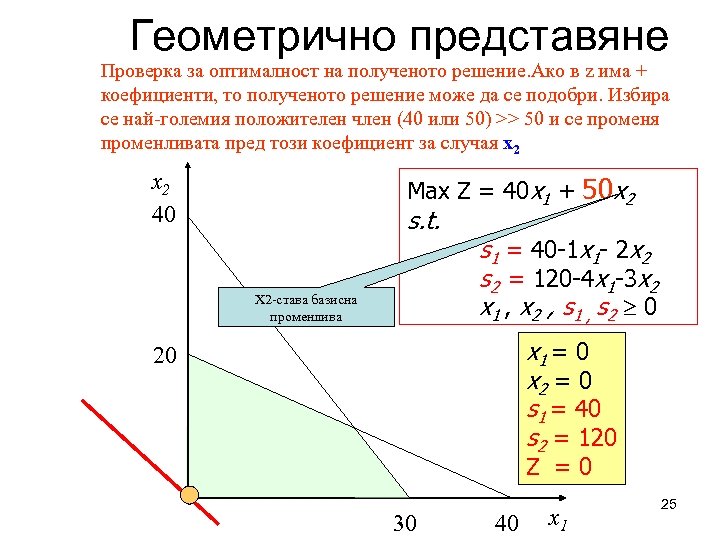 Геометрично представяне Проверка за оптималност на полученото решение. Ако в z има + коефициенти, то полученото решение може да се подобри. Избира се най-големия положителен член (40 или 50) >> 50 и се променя променливата пред този коефициент за случая x 2 40 Max Z = 40 x 1 + 50 x 2 s. t. X 2 -става базисна променлива s 1 = 40 -1 x 1 - 2 x 2 s 2 = 120 -4 x 1 -3 x 2 x 1 , x 2 , s 1 , s 2 0 x 1 = 0 x 2 = 0 s 1 = 40 s 2 = 120 20 Z = 0 30 40 x 1 25
Геометрично представяне Проверка за оптималност на полученото решение. Ако в z има + коефициенти, то полученото решение може да се подобри. Избира се най-големия положителен член (40 или 50) >> 50 и се променя променливата пред този коефициент за случая x 2 40 Max Z = 40 x 1 + 50 x 2 s. t. X 2 -става базисна променлива s 1 = 40 -1 x 1 - 2 x 2 s 2 = 120 -4 x 1 -3 x 2 x 1 , x 2 , s 1 , s 2 0 x 1 = 0 x 2 = 0 s 1 = 40 s 2 = 120 20 Z = 0 30 40 x 1 25
 Геометрично представяне Уравненията се видоизменят, като x 1=0. За да останат s 1 и s 2 положителни, то x 2 може да се изменя до 20. В този случай за свободна променлива се приема s 1, а за базисна x 2 40 Max Z = 40 x 1 + 50 x 2 S 1, x 1 -стават свободни променливи S 2, X 2 -стават базисни променливи 20 ? s. t. s 1 = 40 - 2 x 2 s 2 = 120 - 3 x 2 x 1 = 0 s 1 = 0 x 2 = 20 s 2 = 60 Z = 1, 000 30 40 x 1 26
Геометрично представяне Уравненията се видоизменят, като x 1=0. За да останат s 1 и s 2 положителни, то x 2 може да се изменя до 20. В този случай за свободна променлива се приема s 1, а за базисна x 2 40 Max Z = 40 x 1 + 50 x 2 S 1, x 1 -стават свободни променливи S 2, X 2 -стават базисни променливи 20 ? s. t. s 1 = 40 - 2 x 2 s 2 = 120 - 3 x 2 x 1 = 0 s 1 = 0 x 2 = 20 s 2 = 60 Z = 1, 000 30 40 x 1 26
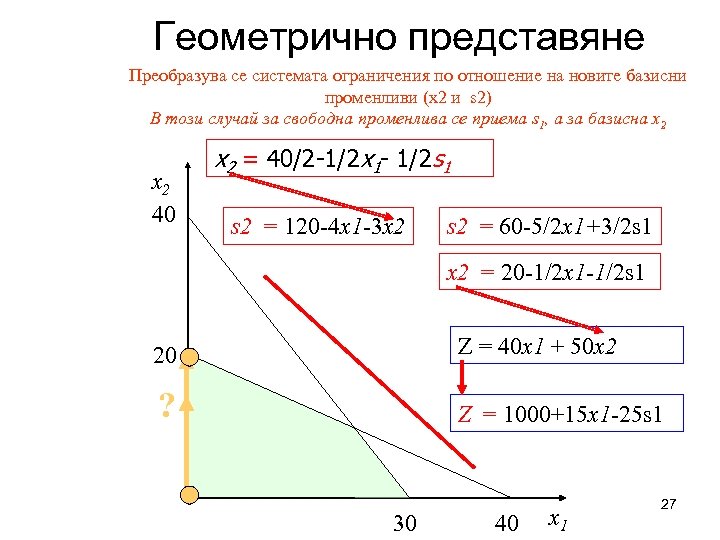 Геометрично представяне Преобразува се системата ограничения по отношение на новите базисни променливи (x 2 и s 2) В този случай за свободна променлива се приема s 1, а за базисна x 2 40 x 2 = 40/2 -1/2 x 1 - 1/2 s 1 s 2 = 120 -4 x 1 -3 x 2 s 2 = 60 -5/2 x 1+3/2 s 1 x 2 = 20 -1/2 x 1 -1/2 s 1 20 Z = 40 x 1 + 50 x 2 ? Z = 1000+15 x 1 -25 s 1 30 40 x 1 27
Геометрично представяне Преобразува се системата ограничения по отношение на новите базисни променливи (x 2 и s 2) В този случай за свободна променлива се приема s 1, а за базисна x 2 40 x 2 = 40/2 -1/2 x 1 - 1/2 s 1 s 2 = 120 -4 x 1 -3 x 2 s 2 = 60 -5/2 x 1+3/2 s 1 x 2 = 20 -1/2 x 1 -1/2 s 1 20 Z = 40 x 1 + 50 x 2 ? Z = 1000+15 x 1 -25 s 1 30 40 x 1 27
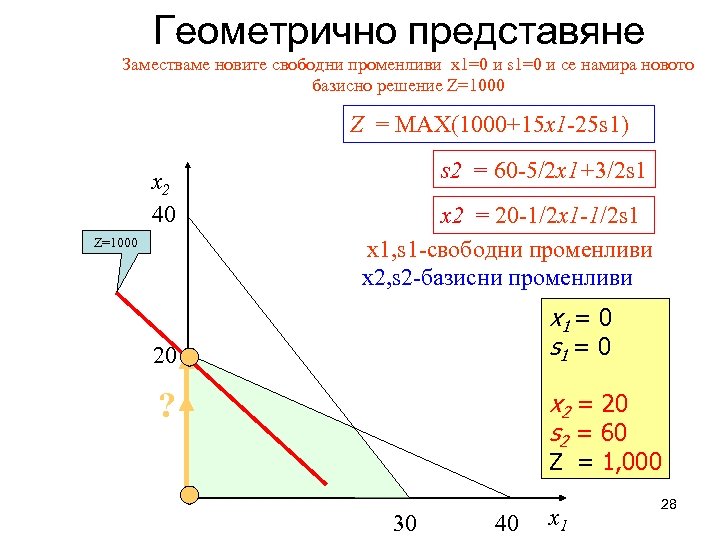 Геометрично представяне Заместваме новите свободни променливи x 1=0 и s 1=0 и се намира новото базисно решение Z=1000 Z = MAX(1000+15 x 1 -25 s 1) x 2 40 Z=1000 s 2 = 60 -5/2 x 1+3/2 s 1 x 2 = 20 -1/2 x 1 -1/2 s 1 x 1, s 1 -свободни променливи x 2, s 2 -базисни променливи x 1 = 0 s 1 = 0 20 ? x 2 = 20 s 2 = 60 Z = 1, 000 30 40 x 1 28
Геометрично представяне Заместваме новите свободни променливи x 1=0 и s 1=0 и се намира новото базисно решение Z=1000 Z = MAX(1000+15 x 1 -25 s 1) x 2 40 Z=1000 s 2 = 60 -5/2 x 1+3/2 s 1 x 2 = 20 -1/2 x 1 -1/2 s 1 x 1, s 1 -свободни променливи x 2, s 2 -базисни променливи x 1 = 0 s 1 = 0 20 ? x 2 = 20 s 2 = 60 Z = 1, 000 30 40 x 1 28
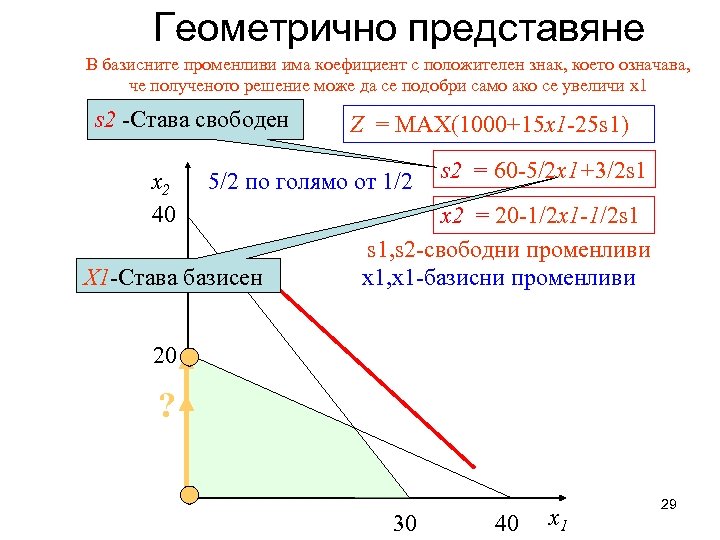 Геометрично представяне В базисните променливи има коефициент с положителен знак, което означава, че полученото решение може да се подобри само ако се увеличи x 1 s 2 -Става свободен x 2 40 Z = MAX(1000+15 x 1 -25 s 1) 5/2 по голямо от 1/2 X 1 -Става базисен s 2 = 60 -5/2 x 1+3/2 s 1 x 2 = 20 -1/2 x 1 -1/2 s 1 s 1, s 2 -свободни променливи x 1, x 1 -базисни променливи 20 ? 30 40 x 1 29
Геометрично представяне В базисните променливи има коефициент с положителен знак, което означава, че полученото решение може да се подобри само ако се увеличи x 1 s 2 -Става свободен x 2 40 Z = MAX(1000+15 x 1 -25 s 1) 5/2 по голямо от 1/2 X 1 -Става базисен s 2 = 60 -5/2 x 1+3/2 s 1 x 2 = 20 -1/2 x 1 -1/2 s 1 s 1, s 2 -свободни променливи x 1, x 1 -базисни променливи 20 ? 30 40 x 1 29
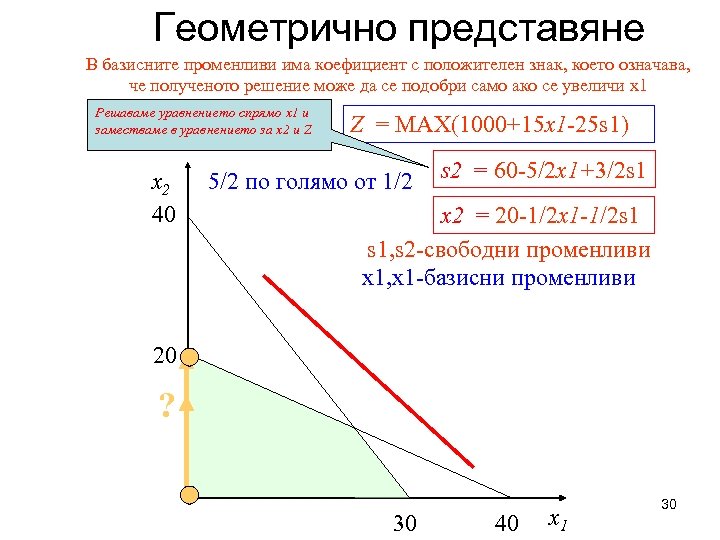 Геометрично представяне В базисните променливи има коефициент с положителен знак, което означава, че полученото решение може да се подобри само ако се увеличи x 1 Решаваме уравнението спрямо x 1 и заместваме в уравнението за x 2 и Z x 2 40 Z = MAX(1000+15 x 1 -25 s 1) 5/2 по голямо от 1/2 s 2 = 60 -5/2 x 1+3/2 s 1 x 2 = 20 -1/2 x 1 -1/2 s 1 s 1, s 2 -свободни променливи x 1, x 1 -базисни променливи 20 ? 30 40 x 1 30
Геометрично представяне В базисните променливи има коефициент с положителен знак, което означава, че полученото решение може да се подобри само ако се увеличи x 1 Решаваме уравнението спрямо x 1 и заместваме в уравнението за x 2 и Z x 2 40 Z = MAX(1000+15 x 1 -25 s 1) 5/2 по голямо от 1/2 s 2 = 60 -5/2 x 1+3/2 s 1 x 2 = 20 -1/2 x 1 -1/2 s 1 s 1, s 2 -свободни променливи x 1, x 1 -базисни променливи 20 ? 30 40 x 1 30
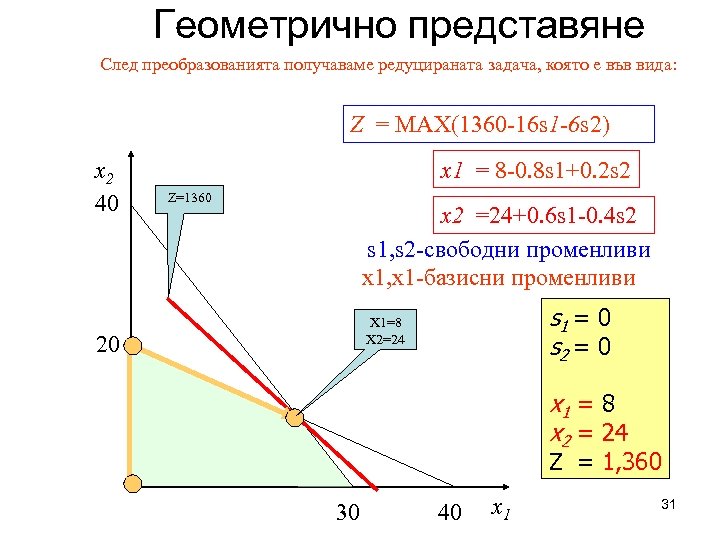 Геометрично представяне След преобразованията получаваме редуцираната задача, която е във вида: Z = MAX(1360 -16 s 1 -6 s 2) x 2 40 x 1 = 8 -0. 8 s 1+0. 2 s 2 Z=1360 x 2 =24+0. 6 s 1 -0. 4 s 2 s 1, s 2 -свободни променливи x 1, x 1 -базисни променливи s 1 = 0 s 2 = 0 X 1=8 X 2=24 20 x 1 = 8 x 2 = 24 Z = 1, 360 30 40 x 1 31
Геометрично представяне След преобразованията получаваме редуцираната задача, която е във вида: Z = MAX(1360 -16 s 1 -6 s 2) x 2 40 x 1 = 8 -0. 8 s 1+0. 2 s 2 Z=1360 x 2 =24+0. 6 s 1 -0. 4 s 2 s 1, s 2 -свободни променливи x 1, x 1 -базисни променливи s 1 = 0 s 2 = 0 X 1=8 X 2=24 20 x 1 = 8 x 2 = 24 Z = 1, 360 30 40 x 1 31
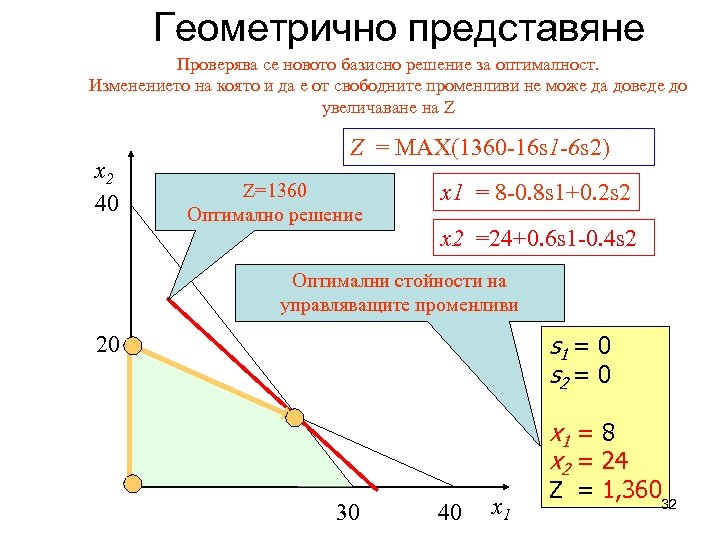 Геометрично представяне Проверява се новото базисно решение за оптималност. Изменението на която и да е от свободните променливи не може да доведе до увеличаване на Z x 2 40 Z = MAX(1360 -16 s 1 -6 s 2) Z=1360 Оптимално решение x 1 = 8 -0. 8 s 1+0. 2 s 2 x 2 =24+0. 6 s 1 -0. 4 s 2 Оптимални стойности на управляващите променливи s 1 = 0 s 2 = 0 20 x 1 = 8 x 2 = 24 30 40 x 1 Z = 1, 36032
Геометрично представяне Проверява се новото базисно решение за оптималност. Изменението на която и да е от свободните променливи не може да доведе до увеличаване на Z x 2 40 Z = MAX(1360 -16 s 1 -6 s 2) Z=1360 Оптимално решение x 1 = 8 -0. 8 s 1+0. 2 s 2 x 2 =24+0. 6 s 1 -0. 4 s 2 Оптимални стойности на управляващите променливи s 1 = 0 s 2 = 0 20 x 1 = 8 x 2 = 24 30 40 x 1 Z = 1, 36032
 33
33
 34
34
 Algebraic Representation Max Z = 40 x 1 + 50 x 2 s. t. 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 • 2 equations in 4 unknowns • Multiple solutions (4 feasible) • Guided search to move to optimal solution • “Simplex Method” 35
Algebraic Representation Max Z = 40 x 1 + 50 x 2 s. t. 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 • 2 equations in 4 unknowns • Multiple solutions (4 feasible) • Guided search to move to optimal solution • “Simplex Method” 35
 Algebraic Representation Max Z = 40 x 1 + 50 x 2 s. t. 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 Simplex Method Tableau 36
Algebraic Representation Max Z = 40 x 1 + 50 x 2 s. t. 1 x 1 + 2 x 2 + s 1 = 40 4 x 1 + 3 x 2 + s 2 = 120 Simplex Method Tableau 36
 Simplex Method • • s 1 and s 2 represent “basic” variables x 1 and x 2 are “non-basic” variables Basic solutions represent corner points Systematically change basic solution to improve objective function … • … while maintaining feasibility! 37
Simplex Method • • s 1 and s 2 represent “basic” variables x 1 and x 2 are “non-basic” variables Basic solutions represent corner points Systematically change basic solution to improve objective function … • … while maintaining feasibility! 37
 Another Simplex Example Max Z = x 1 + 2 x 2 + 2 x 3 s. t. 5 x 1 + 2 x 2 + 3 x 3 15 x 1 + 4 x 2 + 2 x 3 12 2 x 1 + 3 x 3 8 x 1 , x 2 , x 3 0 38
Another Simplex Example Max Z = x 1 + 2 x 2 + 2 x 3 s. t. 5 x 1 + 2 x 2 + 3 x 3 15 x 1 + 4 x 2 + 2 x 3 12 2 x 1 + 3 x 3 8 x 1 , x 2 , x 3 0 38
 Yet Another Simplex Example Max Z = 4, 500 x 1 + 4, 500 x 2 s. t. x 1 1 x 2 1 5, 000 x 1 + 4, 000 x 2 6, 000 400 x 1 + 500 x 2 600 x 1 , x 2 0 39
Yet Another Simplex Example Max Z = 4, 500 x 1 + 4, 500 x 2 s. t. x 1 1 x 2 1 5, 000 x 1 + 4, 000 x 2 6, 000 400 x 1 + 500 x 2 600 x 1 , x 2 0 39
 Theory of the Simplex Method • The optimal solution of an LP must be a corner-point feasible (CPF) solution • If there alternate optima, then at least two must be adjacent CPF solutions • There a finite number of CPF solutions • A CPF solution is optimal if there are no other adjacent CPF solutions that are better 40
Theory of the Simplex Method • The optimal solution of an LP must be a corner-point feasible (CPF) solution • If there alternate optima, then at least two must be adjacent CPF solutions • There a finite number of CPF solutions • A CPF solution is optimal if there are no other adjacent CPF solutions that are better 40
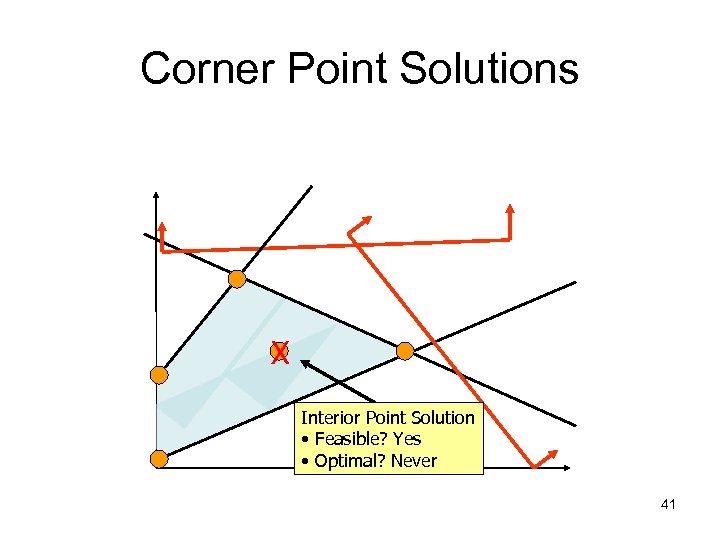 Corner Point Solutions X Interior Point Solution • Feasible? Yes • Optimal? Never 41
Corner Point Solutions X Interior Point Solution • Feasible? Yes • Optimal? Never 41
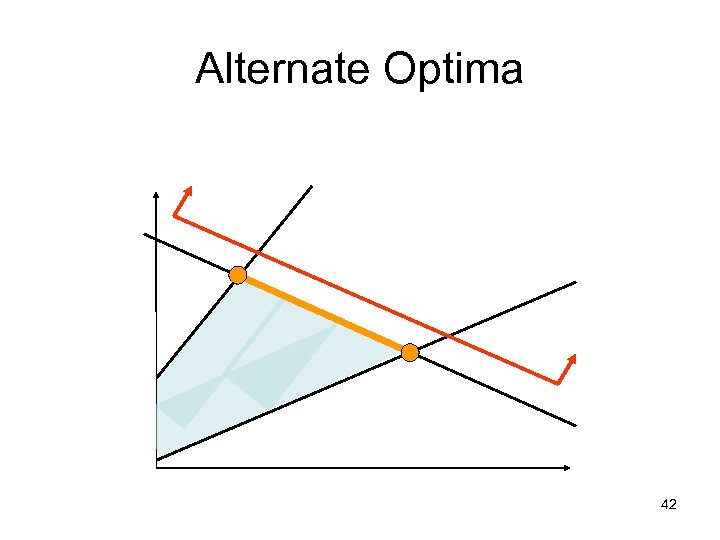 Alternate Optima 42
Alternate Optima 42
 Finite Number of CPF Solutions Example: m=50 constraints, n=100 decision variables Greater than the number of atoms in Universe! 43
Finite Number of CPF Solutions Example: m=50 constraints, n=100 decision variables Greater than the number of atoms in Universe! 43
 Solving Other Types of Linear Programs
Solving Other Types of Linear Programs
 Agenda (review) • The Simplex Method • Simplex Method for max problems • Theory of the Simplex Method • Simplex Method for other LP problems • Unbounded and infeasible problems • Interior point methods 45
Agenda (review) • The Simplex Method • Simplex Method for max problems • Theory of the Simplex Method • Simplex Method for other LP problems • Unbounded and infeasible problems • Interior point methods 45
 Today’s Agenda • Other LP Problems – – – Negative RHS’s Equality constraints Greater than constraints Negative RHS’s Minimization problems • Other Solution Techniques • Extra Credit – Two phase method – Goal programming • LP Solution Problems – Unbounded solutions – No feasible solutions 46
Today’s Agenda • Other LP Problems – – – Negative RHS’s Equality constraints Greater than constraints Negative RHS’s Minimization problems • Other Solution Techniques • Extra Credit – Two phase method – Goal programming • LP Solution Problems – Unbounded solutions – No feasible solutions 46
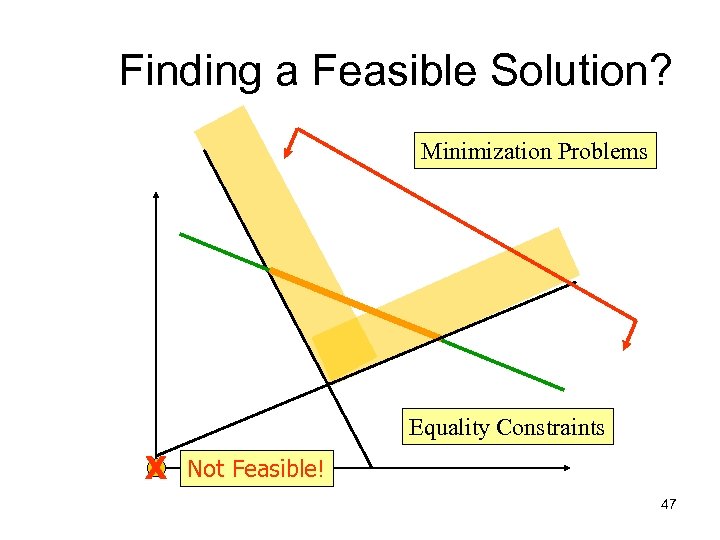 Finding a Feasible Solution? Minimization Problems Equality Constraints X Not Feasible! 47
Finding a Feasible Solution? Minimization Problems Equality Constraints X Not Feasible! 47
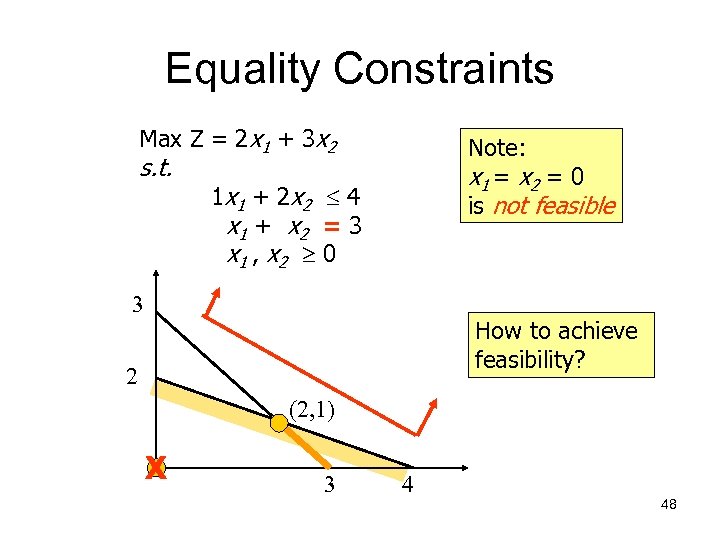 Equality Constraints Max Z = 2 x 1 + 3 x 2 s. t. Note: x 1 = x 2 = 0 is not feasible 1 x 1 + 2 x 2 4 x 1 + x 2 = 3 x 1 , x 2 0 3 How to achieve feasibility? 2 (2, 1) X 3 4 48
Equality Constraints Max Z = 2 x 1 + 3 x 2 s. t. Note: x 1 = x 2 = 0 is not feasible 1 x 1 + 2 x 2 4 x 1 + x 2 = 3 x 1 , x 2 0 3 How to achieve feasibility? 2 (2, 1) X 3 4 48
 Strategy: Start Big M Method feasible, then drive artificial variables from the basis with Max Z = 2 x 1 + 3 x 2 s. t. 1 x 1 + 2 x 2 4 x 1 + x 2 = 3 x 1 , x 2 0 Max Z = 2 x 1 + 3 x 2 s. t. Add artificial variable a 1 M - M a 1 M is a VERY big number 1 x 1 + 2 x 2 + s 1 = 4 x 1 + x 2 + a 1 = 3 Note: x 1 , x 2 , s 1, a 1 0 x 1 = x 2 = 0 is now feasible 49
Strategy: Start Big M Method feasible, then drive artificial variables from the basis with Max Z = 2 x 1 + 3 x 2 s. t. 1 x 1 + 2 x 2 4 x 1 + x 2 = 3 x 1 , x 2 0 Max Z = 2 x 1 + 3 x 2 s. t. Add artificial variable a 1 M - M a 1 M is a VERY big number 1 x 1 + 2 x 2 + s 1 = 4 x 1 + x 2 + a 1 = 3 Note: x 1 , x 2 , s 1, a 1 0 x 1 = x 2 = 0 is now feasible 49
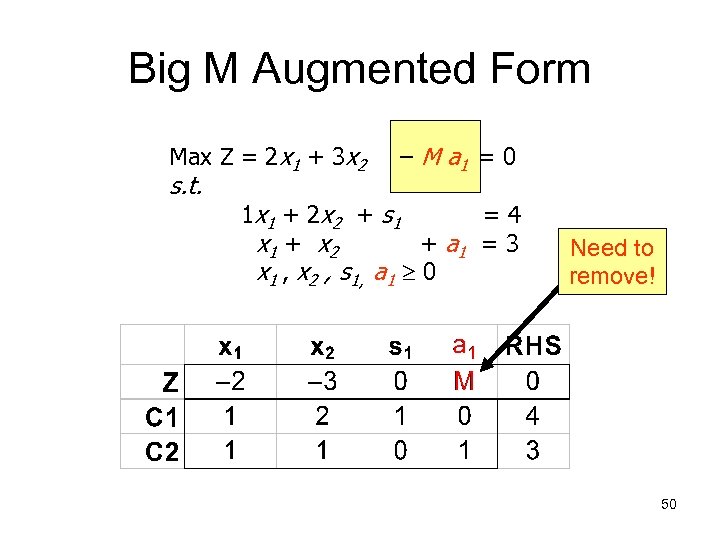 Big M Augmented Form Max Z = 2 x 1 + 3 x 2 s. t. – M a 1 = 0 1 x 1 + 2 x 2 + s 1 = 4 x 1 + x 2 + a 1 = 3 x 1 , x 2 , s 1, a 1 0 Need to remove! 50
Big M Augmented Form Max Z = 2 x 1 + 3 x 2 s. t. – M a 1 = 0 1 x 1 + 2 x 2 + s 1 = 4 x 1 + x 2 + a 1 = 3 x 1 , x 2 , s 1, a 1 0 Need to remove! 50
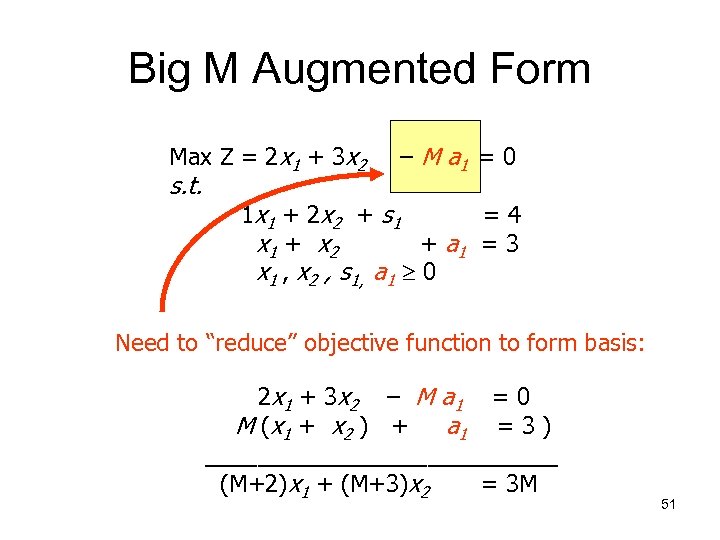 Big M Augmented Form Max Z = 2 x 1 + 3 x 2 s. t. – M a 1 = 0 1 x 1 + 2 x 2 + s 1 = 4 x 1 + x 2 + a 1 = 3 x 1 , x 2 , s 1, a 1 0 Need to “reduce” objective function to form basis: 2 x 1 + 3 x 2 – M a 1 = 0 M (x 1 + x 2 ) + a 1 = 3 ) ______________ (M+2)x 1 + (M+3)x 2 = 3 M 51
Big M Augmented Form Max Z = 2 x 1 + 3 x 2 s. t. – M a 1 = 0 1 x 1 + 2 x 2 + s 1 = 4 x 1 + x 2 + a 1 = 3 x 1 , x 2 , s 1, a 1 0 Need to “reduce” objective function to form basis: 2 x 1 + 3 x 2 – M a 1 = 0 M (x 1 + x 2 ) + a 1 = 3 ) ______________ (M+2)x 1 + (M+3)x 2 = 3 M 51
 Big M Tableau Max Z = (M+2)x 1 + (M+3)x 2 = 3 M s. t. 1 x 1 + 2 x 2 + s 1 = 4 x 1 + x 2 + a 1 = 3 x 1 , x 2 , s 1, a 1 0 Initial Solution x 1 = 0 x 2 = 0 s 1 = 4 a 1 = 3 52
Big M Tableau Max Z = (M+2)x 1 + (M+3)x 2 = 3 M s. t. 1 x 1 + 2 x 2 + s 1 = 4 x 1 + x 2 + a 1 = 3 x 1 , x 2 , s 1, a 1 0 Initial Solution x 1 = 0 x 2 = 0 s 1 = 4 a 1 = 3 52
 “Greater Than” Constraints Max Z = 2 x 1 + 5 x 2 + 3 x 3 s. t. 1 x 1 – 2 x 2 + x 3 20 2 x 1 + 4 x 2 + x 3 = 50 x 1 , x 2 , x 3 0 Subtract slack variable to create equality 1 x 1 – 2 x 2 + x 3 – s 1 = 20 Add artificial variable for equality… 1 x 1 – 2 x 2 + x 3 – s 1 + a 1 = 50 53
“Greater Than” Constraints Max Z = 2 x 1 + 5 x 2 + 3 x 3 s. t. 1 x 1 – 2 x 2 + x 3 20 2 x 1 + 4 x 2 + x 3 = 50 x 1 , x 2 , x 3 0 Subtract slack variable to create equality 1 x 1 – 2 x 2 + x 3 – s 1 = 20 Add artificial variable for equality… 1 x 1 – 2 x 2 + x 3 – s 1 + a 1 = 50 53
 “Greater-Than” Big M Max Z = x 1 + 2 x 2 + 2 x 3 s. t. – Ma 1 – Ma 2 = 0 1 x 1 – 2 x 2 + x 3 – s 1 + a 1 = 20 2 x 1 + 4 x 2 + x 3 + + a 2 = 50 x 1 , x 2 , x 3 , s 1 , a 2 0 Tableau with reduced objective function: 54
“Greater-Than” Big M Max Z = x 1 + 2 x 2 + 2 x 3 s. t. – Ma 1 – Ma 2 = 0 1 x 1 – 2 x 2 + x 3 – s 1 + a 1 = 20 2 x 1 + 4 x 2 + x 3 + + a 2 = 50 x 1 , x 2 , x 3 , s 1 , a 2 0 Tableau with reduced objective function: 54
 Negative Variables xj allowed to be any value (+ or –) Substitute xj = xj+ – xj+ , xj – 0 55
Negative Variables xj allowed to be any value (+ or –) Substitute xj = xj+ – xj+ , xj – 0 55
 Negative RHS’s 0. 4 x 1 – 0. 3 x 2 – 10 Is exactly equivalent to Multiply by – 1 – 0. 4 x 1 + 0. 3 x 2 10 56
Negative RHS’s 0. 4 x 1 – 0. 3 x 2 – 10 Is exactly equivalent to Multiply by – 1 – 0. 4 x 1 + 0. 3 x 2 10 56
 Minimization Problems Min Z = 0. 4 x 1 + 0. 3 x 2 Is exactly equivalent to Multiply by – 1 Max Z = – 0. 4 x 1 – 0. 3 x 2 57
Minimization Problems Min Z = 0. 4 x 1 + 0. 3 x 2 Is exactly equivalent to Multiply by – 1 Max Z = – 0. 4 x 1 – 0. 3 x 2 57
 LP Solution Problems • Unbounded Solutions • No Feasible Solutions 58
LP Solution Problems • Unbounded Solutions • No Feasible Solutions 58
 Unbounded Solutions 40/0= 120/0= • • Pivot cell is zero Can bring in unlimited x 2 Z increases without limit! LP is “unbounded” 59
Unbounded Solutions 40/0= 120/0= • • Pivot cell is zero Can bring in unlimited x 2 Z increases without limit! LP is “unbounded” 59
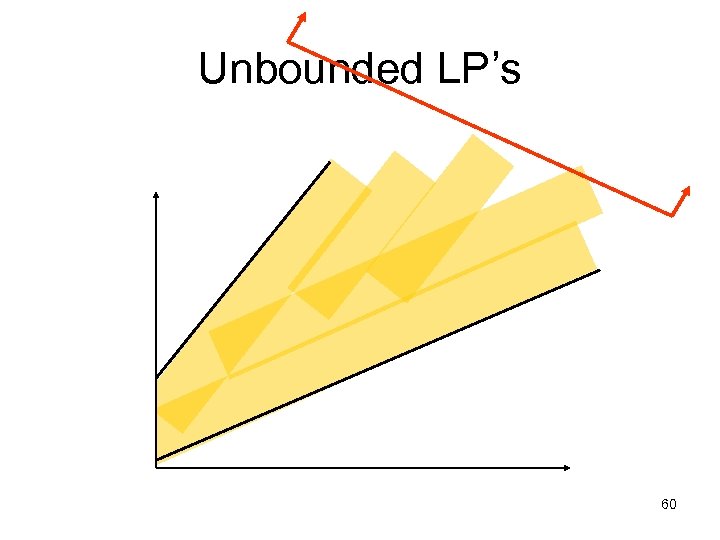 Unbounded LP’s 60
Unbounded LP’s 60
 No Feasible Solutions An LP is infeasible if an artificial variable remains basic in the optimal solution 61
No Feasible Solutions An LP is infeasible if an artificial variable remains basic in the optimal solution 61
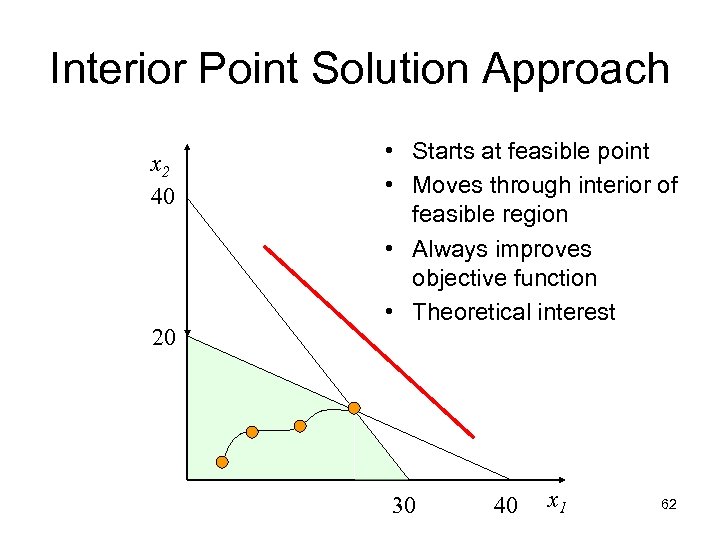 Interior Point Solution Approach x 2 40 20 • Starts at feasible point • Moves through interior of feasible region • Always improves objective function • Theoretical interest 30 40 x 1 62
Interior Point Solution Approach x 2 40 20 • Starts at feasible point • Moves through interior of feasible region • Always improves objective function • Theoretical interest 30 40 x 1 62
 Next week… LP Sensitivity and Duality
Next week… LP Sensitivity and Duality


