ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

• • • Вычисление площадей плоских фигур • Пример Вычисление площади фигуры в полярной системе координат • Пример Вычисление объема тел • Пример Вычисление длины дуги • Пример Вычисление площади поверхности тела вращения • Пример инженерной задачи

y S – площадь криволинейной трапеции, ограниченной сверху графиком функции, снизу осью абсцисс x , двумя прямыми x = a и x = b , параллельными оси ординат. Пример: вычислить площадь фигуры, ограниченной косинусоидой и синусоидой y cos x x -5 p /4 sin x f(x) S a x b

@ Найти площадь фигуры, ограниченной прямой, параболой и осью x y Точки пересечения кривых : (0; 0), (2; 0), (4; 2) Первое решение : S 2 S 1 0 x 2 4 Второе решение :

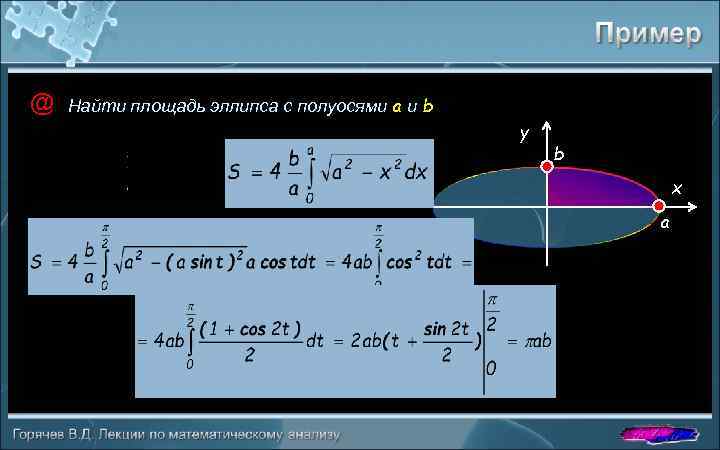@ Найти площадь эллипса с полуосями a и b y b x a

@ Найти площадь астроиды : Используем уравнение астроиды в параметрической форме

r ( jb ) b dl = r dj M(x, y) dj r j 0 x y a r ( ja ) 0 r(j)

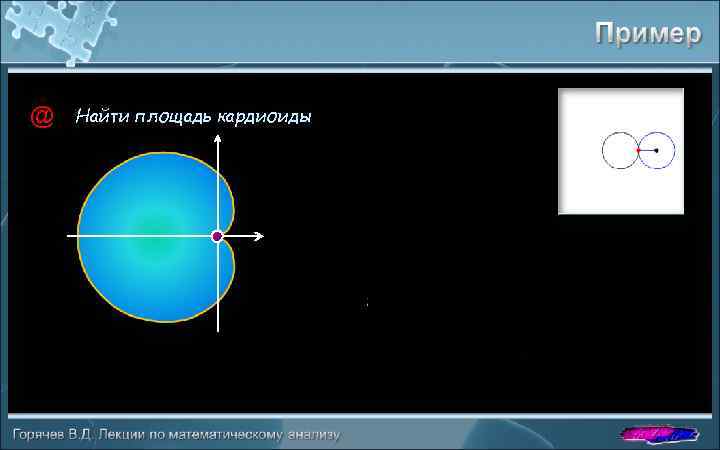@ Найти площадь кардиоиды

В общем случае для этих целей используются двойной или тройной интеграл. В частном случае, если известны площади параллельных сечений вдоль выбранного направления, можно получить расчетную формулу для объема.

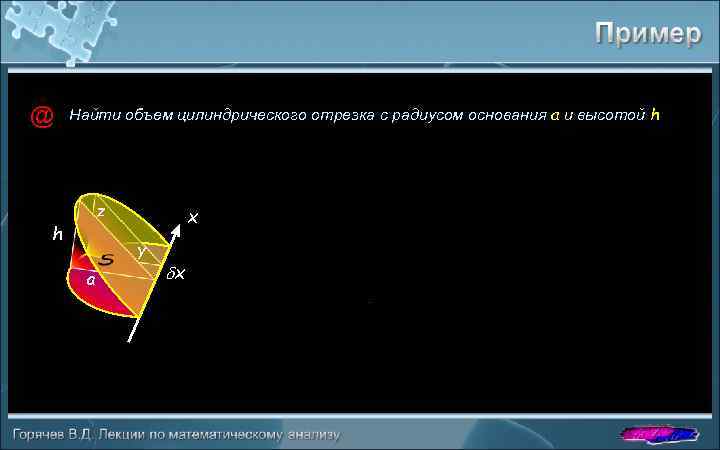@ Найти объем цилиндрического отрезка с радиусом основания a и высотой h z h x y a dx

y x

@ Найти объем шара радиуса a y x

@ Найти объем тора с радиусами R = 2 и a = 1 x R a

B dz dx A dy Плоская кривая 0

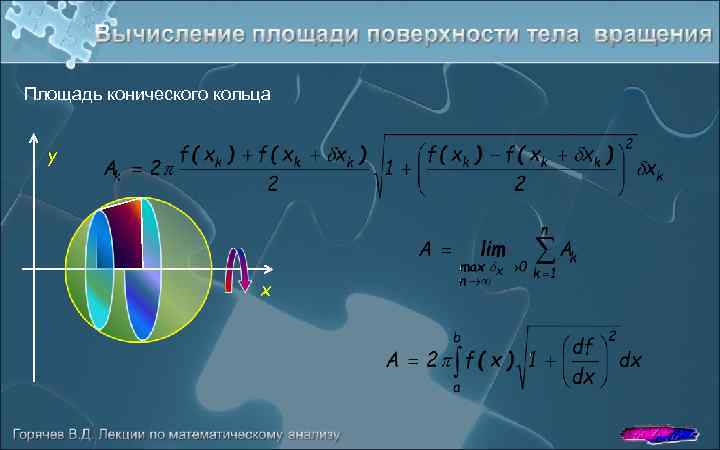Площадь конического кольца y x

@ Найти площадь сферы радиуса a y x

@ Найти силу давления воды на стенку шлюза в форме полукруга радиуса R, диаметр которого совпадает с поверхностью воды O R x r dx R