Прикладные задачи динамики космического полёта Лектор Храмов

Прикладные задачи динамики космического полёта Лектор – Храмов Андрей Александрович, старший преподаватель кафедры космического машиностроения, к. т. н. Определения: Прикладная задача - задача, решение которой имеет практическое значение. Динамика полёта - научная дисциплина, которая рассматривает вопросы, связанные с исследованием траекторий движения летательного аппарата, его устойчивости и управляемости. Космический аппарат (КА) - общее название технических устройств, используемых для выполнения разнообразных задач в космическом пространстве, а также проведения исследовательских и иного рода работ на поверхности различных небесных тел. Будем считать космическими аппаратами такие объекты как: ракеты-носители (аппараты, обеспечивающие выведение космических объектов на орбиты спутников Земли с её поверхности); искусственные спутники Земли, космические станции и платформы; разгонные блоки, обеспечивающие перевод космического объекта с одной орбиты на другую (межорбитальные перелёты); спускаемые на Землю из космоса КА; лунные и межпланетные космические аппараты, их отдельные отделяемые части, которые обеспечивают операции посадки на поверхности планет, орбитального маневрирования или операций возврата КА к Земле.

Траектория КА - некоторая кривая в рассматриваемом пространстве, характеризующая перемещение космического аппарата и определяющая положение его центра масс. В курсе рассматривается комплекс проблем, которые определяют траекторию КА, дают возможность анализировать траекторию, выбирать её для решения той или иной транспортной, народно-хозяйственной, коммерческой или научной задачи, которая стоит перед КА. Отметим, что реальный КА это не твердое тело, он включает ёмкости, частично заполненные жидкостью, он имеет определённую жёсткость с определёнными «жёсткостными» характеристиками, которые приводят к очень сложному перемещению (например, колебанию) одних частей КА относительно других частей. В нашем курсе мы будем считать (это оказывается допустимым и обоснованным при анализе многих проблем), что КА это жесткое твердое тело переменной массы, движение которого характеризуется тремя поступательными степенями свободы и тремя вращательными степенями свободы. Причем главными для нас будут поступательные степени свободы, определяющие траекторию КА. Для определения характеристик движения, законов управления движением и траектории КА необходима математическая модель движения - полная (замкнутая) система уравнений. Как правило это система обыкновенных дифференциальных уравнений.

Тема 1: Траектории движения ракеты-носителя при выведении космического аппарата на околоземную орбиту Ракета-носитель для выведения на орбиту спутника Земли должна обеспечить: – определенную высоту КА; – определенную скорость КА; – определенный угол между скоростью КА и плоскостью местного горизонта (плоскостью, перпендикулярной радиус-вектору КА). Выбор условий старта Геоцентрическая широта космодрома – определяет скорость движения космодрома (начальную скорость ракеты-носителя) в инерциальном пространстве. Скорость движения космодрома направлена по местной параллели, а её величина равна произведению угловой скорости вращения Земли (7, 29*10 -5 рад/с) на расстояние космодрома от оси Земли ( ). Азимут запуска - угол между северным направлением меридиана и направлением запуска ракеты-носителя. При азимуте запуска +90 градусов масса выводимого спутника максимальна; при этом наклонение орбиты будет равно геоцентрической широте космодрома. Допустимые азимуты запуска ограничены допустимыми трассами ракетыносителя: - трасса должна выбираться так, чтобы она не проходила над сильно населенными районами Земли; - отработанные конструкции (ускорители) должны падать в специальных зонах земной поверхности (зонах отчуждения).

К определению азимута запуска Азимут движения в точке старта вычисляется по формуле: Скорость полёта в конце участка выведения в стартовой системе координат равен: Азимут запуска рассчитывается по формуле:

Характеристики космодромов

Понятие характеристической скорости Характеристической скоростью (идеальной скоростью) летательного аппарата называют скорость, которую теоретически он может развить под действием реактивных сил, двигаясь прямолинейно в вакууме при отсутствии гравитации. Эта скорость определяется известной формулой Циолковского: Для многоступенчатого РН: Характеристическая скорость (располагаемая характеристическая скорость) – энергетическая характеристика ракеты-носителя. Потребная характеристическая скорость - скорость, необходимая для выведения КА на заданную орбиту под действием силы тяги двигателей в условиях действия внешних сил. Является энергетической характеристикой космической операции. где - идеальная потребная характеристическая скорость запуска - скорость, которая должна быть сообщена КА на поверхности Земли мгновенным импульсом, чтобы он вышел без сопротивления атмосферы в точку, соответствующую концу активного участка, с заданной орбитальной скоростью, - гравитационные потери, - аэродинамические потери, - потери на управление. Условие возможности выведения: .

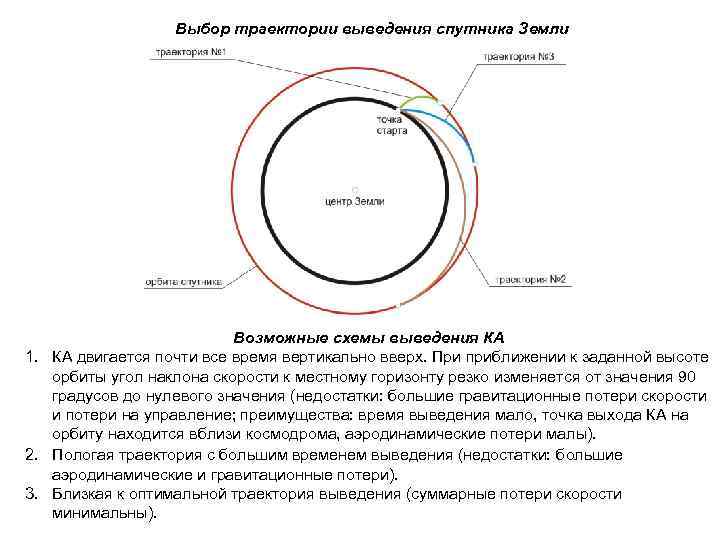Выбор траектории выведения спутника Земли Возможные схемы выведения КА 1. КА двигается почти все время вертикально вверх. При приближении к заданной высоте орбиты угол наклона скорости к местному горизонту резко изменяется от значения 90 градусов до нулевого значения (недостатки: большие гравитационные потери скорости и потери на управление; преимущества: время выведения мало, точка выхода КА на орбиту находится вблизи космодрома, аэродинамические потери малы). 2. Пологая траектория с большим временем выведения (недостатки: большие аэродинамические и гравитационные потери). 3. Близкая к оптимальной траектория выведения (суммарные потери скорости минимальны).

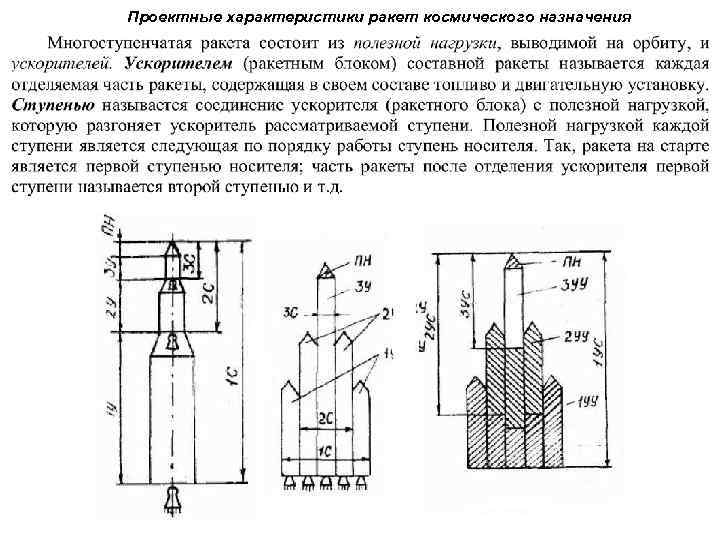Проектные характеристики ракет космического назначения

Траекторию полёта можно разделить на ряд участков, отличающихся по своей специфике: 1. Стартовый участок 2. Полёт первой ступени 3. Разделение ступеней 4. Полёт второй и последующих ступеней 5. Отделение полезной нагрузки 1. Стартовый участок Этот участок начинается в момент поступления сигнала о начальном перемещении РН (на несколько сантиметров над стартовым столом), и заканчивается подъёмом на высоту нескольких десятков метров. Характер движения на стартовом участке и нагрузки, действующие на РН, определяются типом стартового устройства: - открытая или частично углубленная; - шахтная (свободный старт, старт по направляющим). 2. Участок полёта первой ступени Полёт первой ступени проходит в плотных слоях атмосферы при начальной тяговооружённости (отношения земной тяги двигателей первой ступени к её начальному весу) больше единицы. Обычно для многоступенчатых РН высота в конце участка работы двигателей первой ступени достигает 40… 60 км. Выключение двигателей производится после достижения, например, определённого значения скорости или по сигналу выгорания одного из компонентов топлива.

3. Разделение ступеней Участок разделения начинается с момента подачи главной команды на выключение двигательной установки предыдущей ступени и заканчивается, когда отделившийся ускоритель не может влиять на полёт последующей ступени. Возможны две основные схемы разделения: холодное разделение и горячее разделение. Холодное разделение, или разделение торможением отработавшего ускорителя предыдущей ступени, имеет место в том случае, когда основной двигатель последующей ступени запускается после достижения безопасного расстояния от отделившегося ускорителя. Горячее, или огневое, разделение происходит, когда двигатель последующей ступени запускается ещё до разрыва механических связей между разделяющимися частями. При этом ускоритель предыдущей ступени отбрасывается струёй истекающих газов включённого двигателя. Важное значение имеет выбор правильного соотношения между моментами времени запуска двигателя последующей ступени, выключения двигателя отделяющегося ускорителя предыдущей ступени и выдачи команды на разрыв связей. При слишком раннем разделении имеет место потеря скорости из-за недоиспользования топлива предыдущей ступени. В случае слишком позднего разделения затрудняется запуск двигателя последующей ступени из-за уменьшения продольной перегрузки.

4. Участки полёта второй и последующих ступеней Полёт летательных аппаратов на участке работы второй и последующих ступеней протекает, в условиях пренебрежимо малых аэродинамических нагрузок из-за разрежённости атмосферы. Это позволяет снять ограничение на допустимые углы атаки (не более 2… 3 ), которое является обязательным для участка полёта первой ступени. В результате появляется возможность использования оптимальных законов управления. Начальные тяговооружённости верхних ступеней могут быть меньше единицы, поскольку траектория полёта на участках работы этих ступеней существенно отклоняется от вертикали. Как правило, на участке работы второй и последующих ступеней выбирается такая траектория, чтобы при отсутствии возмущений углы крена и рыскания равнялись нулю. Тогда существенно упрощаются условия управления по тангажу, которое осуществляется путём поворота продольной оси летательного аппарата в плоскости прицеливания. Обычно программа угла тангажа задаётся в виде зависимости от времени . x y Рысканье Крен z Тангаж Связанная система координат, углы ориентации

Для ракет-носителей программа угла тангажа определяется требованием выведения на заданную орбиту максимальной полезной нагрузки с обеспечением приемлемой точности параметров получаемой орбиты. 5. Участок отделения полезной нагрузки При достижении требуемых параметров движения подаётся главная команда на выключение двигателей. Участок отделения полезной нагрузки начинается с этого момента, а заканчивается после её отхода на безопасное расстояние. Для уменьшения разброса параметров движения в конце активного участка целесообразно уменьшать величину тяги перед выключением двигателя. Траектория полёта полезной нагрузки определяется целевым назначением летательного аппарата. Так, головные части баллистических ракет движутся по траекториям вблизи поверхности Земли, а космические летательные аппараты совершают полёт по околоземным орбитам или межпланетным траекториям. Силы, действующие на ракету-носитель В общем случае считается, что на РН в полёте действуют три силы и моменты, создаваемые ими: - сила земного притяжения, действие которой описывается законом всемирного тяготения Ньютона , где - для центрального поля; - сила тяги, равная сумме реактивной силы и силы статического давления окружающей среды, приходящейся на площадь сопла ракетного двигателя ; - полная аэродинамическая сила, возникающая в результате взаимодействия движущейся РН с атмосферой Земли .

Основные понятия математической модели движения

1. 1 Движение первой ступени ракеты-носителя

Выбор программы полёта первой ступени РН

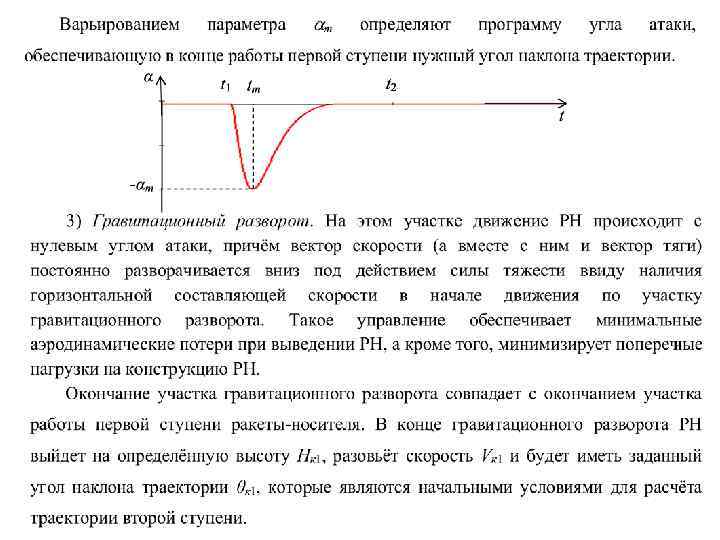
1. 2 Движение второй ступени ракеты-носителя

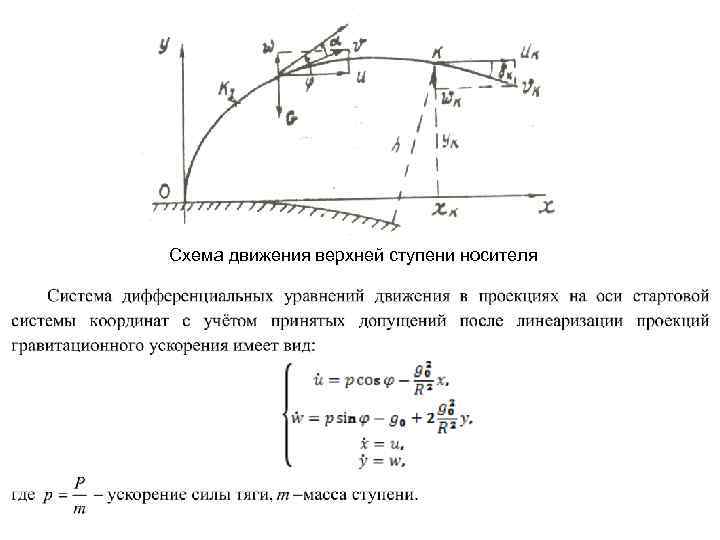Схема движения верхней ступени носителя

Пересчет конечных параметров из стартовой системы координат в инерциальную геоцентрическую систему координат

Определение параметров опорной орбиты КА