ПРИЧИНЫ РАЗРУШЕНИЯ И ОТНОСИТЕЛЬНОЙ СТАБИЛЬНОСТИ ДИСПЕРСНЫХ СИСТЕМ Принципиальная

ПРИЧИНЫ РАЗРУШЕНИЯ И ОТНОСИТЕЛЬНОЙ СТАБИЛЬНОСТИ ДИСПЕРСНЫХ СИСТЕМ Принципиальная термодинамическая неравновесность лиофобных дисперсных систем, связанная с наличием в них значительного избытка свободной поверхностной энергии, обусловливает протекание в них процессов разрушения. Седиментационная и агрегативная устойчивость дисперсных систем. Роль теплового движения. Под устойчивостью лиофобных коллоидных систем подразумевают их способность сохранять постоянными во времени основные параметры: 1) дисперсность; 2) распределение частиц по объему среды. Седиментационная (кинетическая) устойчивость - устойчивость системы против снижения потенциальной энергии частиц дисперсной фазы при их оседании под действием силы тяжести.

Агрегативная устойчивость - способность системы противостоять процессам, ведущим к уменьшению свободной энергии поверхностей раздела частиц дисперсной фазы с дисперсионной средой. Процессами разрушения дисперсных систем, приводящими к уменьшению свободной поверхностной энергии служат: изотермическая перегонка (массоперенгосвещества от малых частиц к более крупным); коалесценция (слияние частиц); коагуляция (агрегирование частиц при их слипании). Изотермическая перегонка и коалесценция - ∆Fs= σ ΔS < 0 Коагуляция - ∆Fs= Δσ S < 0 При одинаковой исходной дисперсности коалесценция и изотермическая перегонка приводят к значительно более резкому уменьшению свободной поверхностной энергии системы, чем коагуляция.

Агрегат (коагулят), содержит N частиц, каждая из которых взаимодействует с Z соседями Число контактов между частицами - ½ ZN Энергия сцепления м/у частицами - ик Выигрыш свободной поверхностной энергии при коагуляции - ½ZNик

Для свободнодисперсных систем природа устойчивости и закономерности разрушения в значительной степени определяются тепловым движением частиц дисперсной фазы. При условии σ ≤ βk. T/αd 2 где α –коэффициент формы; k – постоянная Больцмана. тепловое движение частиц дисперсной фазы при коалесценции и изотермической перегонке обусловливает термодинамическую устойчивость дисперсных систем. Процесс самопроизвольного распада агрегатов (коагулятов) и переход связнодисперсных систем в свободнодисперсные называется пептизацией.

Изменение свободной энергии системы при распаде агрегата. Возрастание свободной энергии системы при полном диспергировании агрегата: ΔFs= 1/2 Z 0 Nuк Повышение энтропии ΔS ≈ β*Nk β* = ln(nа / n. П) Концентрация частиц дисперсной фазы в агрегированном nа и пептизированном п. П состоянии. β* ≈ 10 -20 Общее изменение свободной энергии системы: ΔF = ½ZN uк - β*Nk. T

Условие самопроизвольного диспергирования - Пептизация невыгодна - Условие равновесия между процессами агрегирования и пептизации частиц -

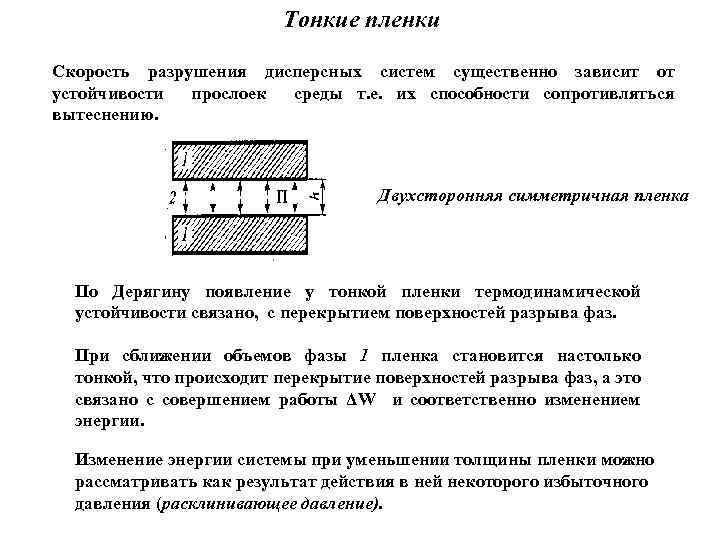
Тонкие пленки Скорость разрушения дисперсных систем существенно зависит от устойчивости прослоек среды т. е. их способности сопротивляться вытеснению. Двухсторонняя симметричная пленка По Дерягину появление у тонкой пленки термодинамической устойчивости связано, с перекрытием поверхностей разрыва фаз. При сближении объемов фазы 1 пленка становится настолько тонкой, что происходит перекрытие поверхностей разрыва фаз, а это связано с совершением работы ΔW и соответственно изменением энергии. Изменение энергии системы при уменьшении толщины пленки можно рассматривать как результат действия в ней некоторого избыточного давления (расклинивающее давление).

Расклинивающее давление П = П(h) избыточное давление, действующее со стороны прослойки на ограничивающие ее поверхности и стремящееся раздвинуть (расклинить) их. Чтобы в равновесном процессе уменьшить толщину прослойки на величину dh, необходимо совершить работу: d. W = - П(h)dh Связь между расклинивающим давлением П, энергией пленки и ее толщиной:

Молекулярная составляющая расклинивающего давления Ионно-электростатическая составляющая расклинивающего давления

Молекулярные взаимодействия в дисперсных системах Энергия притяжения на единицу площади зазора - А = (3/4)πhν 0 a 2 мn 2 - константа Гамакера где число молекул в единице объема взаимодействующих фаз - n, поляризуемостью молекул – ам, энергией ионизации - hv 0 Дифференцирование выражения для по толщине зазора: - молекулярная составляющая расклинивающего давления между двумя конденсированными фазами, разделенными вакуумом.

Взаимодействие двух разных фаз - энергии взаимодействия А* - сложная константа Гамакера Симметричная плена типа 121

Взаимодействие двух сферических частиц радиусом r Сила взаимодействия частиц - Сила притяжения двух одинаковых сферических частиц -

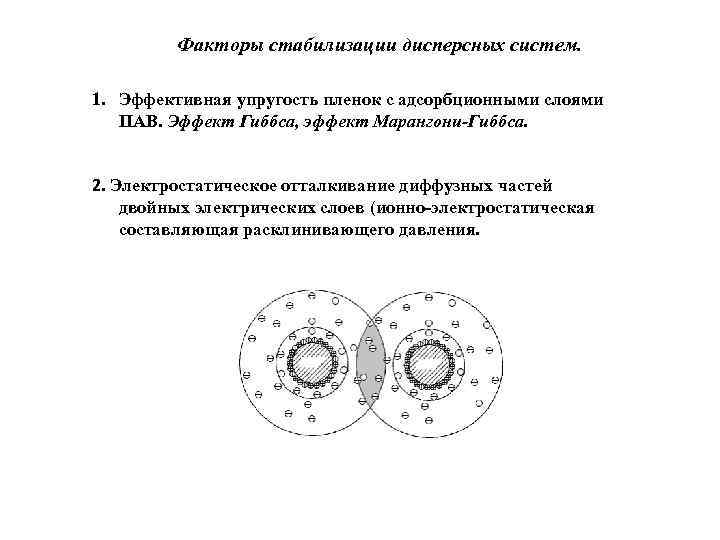
Факторы стабилизации дисперсных систем. 1. Эффективная упругость пленок с адсорбционными слоями ПАВ. Эффект Гиббса, эффект Марангони-Гиббса. 2. Электростатическое отталкивание диффузных частей двойных электрических слоев (ионно-электростатическая составляющая расклинивающего давления.

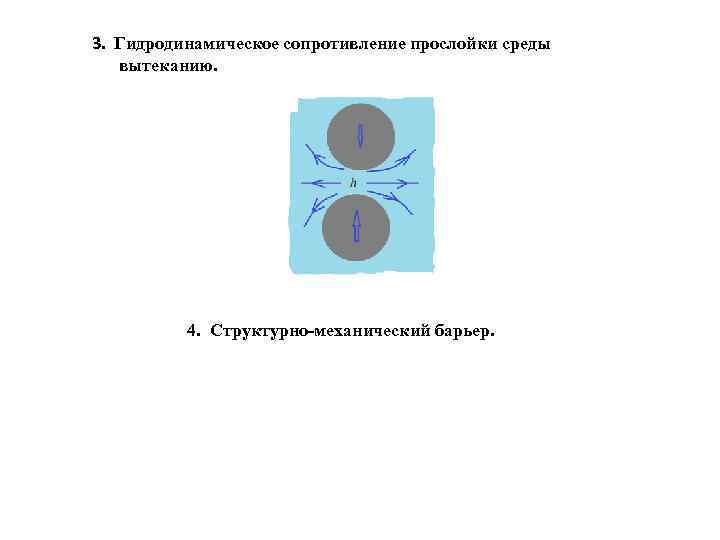
3. Гидродинамическое сопротивление прослойки среды вытеканию. 4. Структурно-механический барьер.

Marian Smoluchowski (1872 -1917)

Wilder Bankroft (1876 -1953)

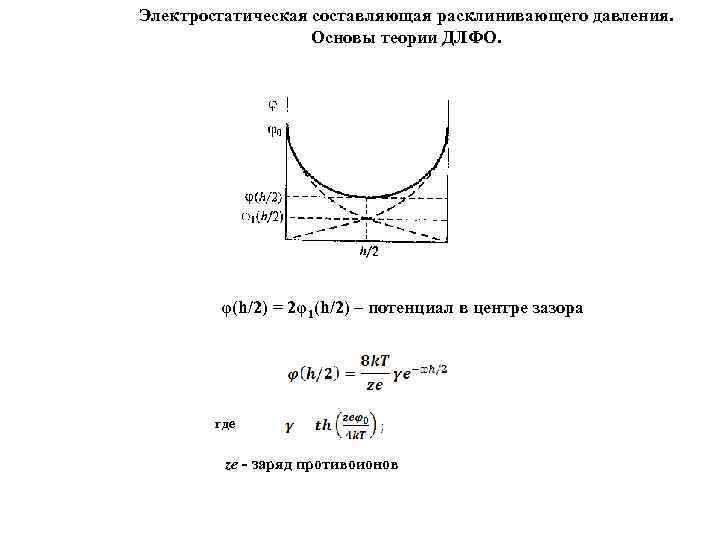
Электростатическая составляющая расклинивающего давления. Основы теории ДЛФО. φ(h/2) = 2φ1(h/2) – потенциал в центре зазора где ze - заряд противоионов

- избыточная плотность заряда ρν(h/2) Произведение ρν(h/2)∙φ(h/2): характеризует плотность электростатической энергии в центре зазора равная расклинивающему давлению (1) Для слабозаряженной поверхности когда - и

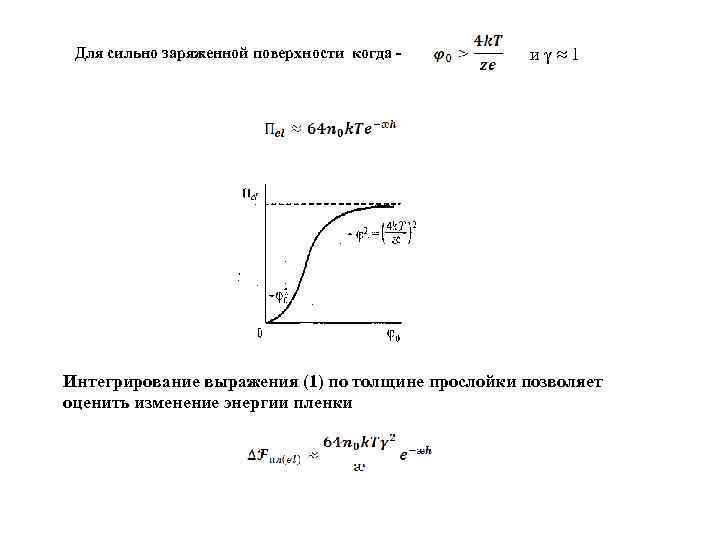
Для сильно заряженной поверхности когда - иγ≈1 Интегрирование выражения (1) по толщине прослойки позволяет оценить изменение энергии пленки

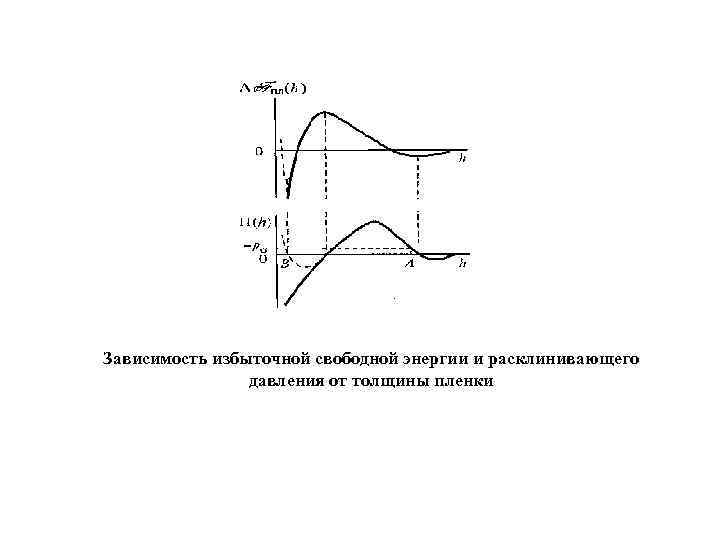
Зависимость избыточной свободной энергии и расклинивающего давления от толщины пленки

∆Fпл= 0 - критическое условие потери устойчивости (2) (3) Деля выражение (2) на (3), находим ӕс = 2/hс или hс = 2ӕс Подставляя найденное значение hc в выражение (2) или (3) Возводя это равенство в квадрат и учитывая, что

где k 1 ≈ 2 • 105 Критическая концентрация электролита, когда исчезает энергетический барьер Для сильно заряженных частиц дисперсной фазы когда γ ≈ 1 Концентрационная коагуляция Для слабозаряженных коллоидных частиц когда γ ≈ zеφо/4 k. Т (5)

где k 2 ≈ 800 Нейтрализационная коагуляция Заменяем в (5) на 1/ӕ 2 c и извлекаем корень квадратный где k 3 ≈ 0, 024

Критерий Эйлерса - Корфа где ξ 2/ӕc = const

Кинетика коагуляции J = kmn пт пn содержащего т - частота столкновения m-мерной частицы (агрегата, первичных частиц) с n-мерной частицей - константа скорости - уравнение Смолуховского t. K = 1 /kn 0 - время половинной коагуляции

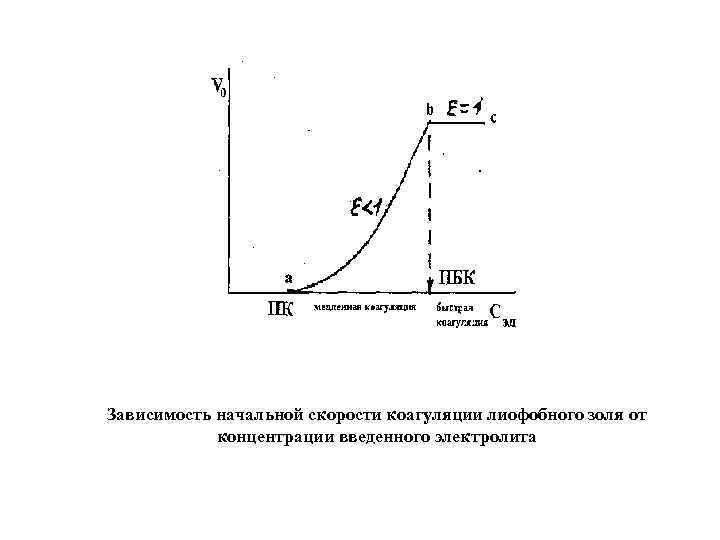
Зависимость начальной скорости коагуляции лиофобного золя от концентрации введенного электролита

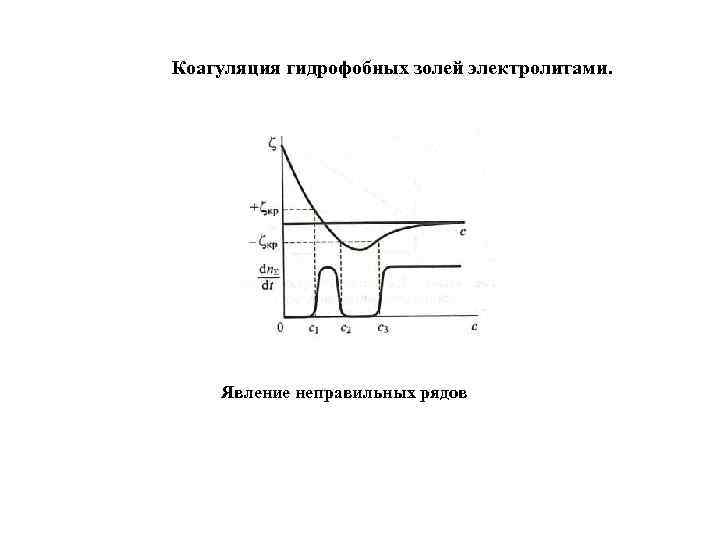
Коагуляция гидрофобных золей электролитами. Явление неправильных рядов