Приближенные методы решения нелинейных алгебраических уравнений.
План лекции 1. Метод простой итерации. 2. Метод половинного деления. 3. Метод касательных. 4. Метод хорд.
. 1. Метод простой итерации. Дано нелинейное алгебраическое уравнение вида f(x)=0. Требуется найти корни данного уравнения с точностью .
1. Метод простой итерации. Алгоритм 1 шаг. Исходное уравнение преобразуют к виду х=y (х). Например: а) f(х)=ех-х-2=0 х=ех-2; y(х)= ех-2. б) f(х)=ех-cos(x) = 0, оно не содержит х в этом случае левую и правую часть уравнения домножают на произвольную const К и прибавляют х, корни от этого не изменятся: (ех-cos(x))*к +х= 0*к+х у(х)=к* ех-к* cos(x)+х;
1. Метод простой итерации. Алгоритм 2 шаг. Выбирают начальное приближение корня. Для этого: а) Приблизительно оценивают на каком отрезке находится корень. Существует два способа: • Графический • Аналитический
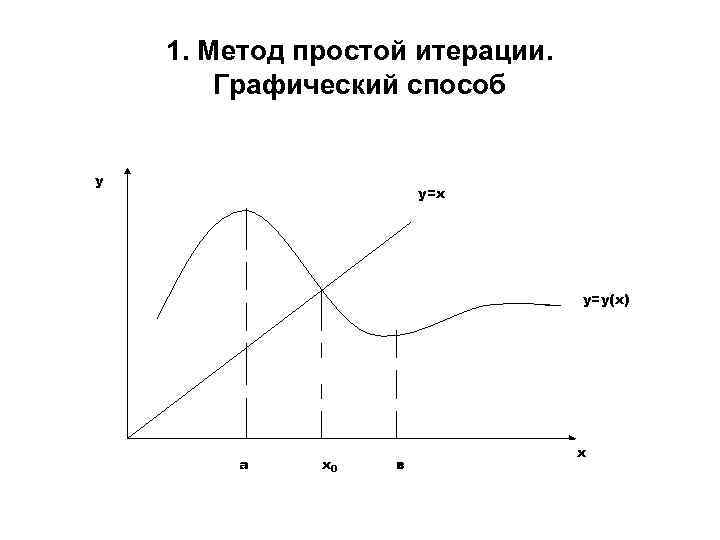
1. Метод простой итерации. Графический способ у у=х у=у(х) а х0 в х
1. Метод простой итерации. Аналитический способ Строят таблицу значений функции у=f(х) на некотором интервале с определенным шагом. Корень находится в том интервале, на концах которого функция имеет разные знаки.
1. Метод простой итерации. Алгоритм б) За первое приближение берут точку х0=(a+b)/2 - середину найденного отрезка. 3 шаг. Вычисляют новые приближения к корню по формуле х1=y(х0), х2=y(х1), …, хк+1=y(хк). Процесс итераций продолжают до тех пор пока разница между соседними приближениями не станет меньше , т. е. |хк+1 - хк|< . Корнем будет последнее найденное приближение.
1. Метод простой итерации. Замечание Итерационный процесс может быть как сходящимся так и расходящимся. В случае расходящегося процесса с каждой итерацией мы отдаляемся от корня. Итерационный процесс является сходящимся: |у’(х)|>1.
1. Метод простой итерации. Замечание Перед составлением программы нужно проанализировать функцию. Если окажется, что |у’(х)|>1, тогда нужно подобрать const к так, чтобы это условие выполнилось. x+k*f(x)=x+0*k y(x)=x+ k*f(x) у’(х)=1+ k*f ’ (x) у’(х)<1, если взять у’(х)=0 k= - 1/ f ’ (x)
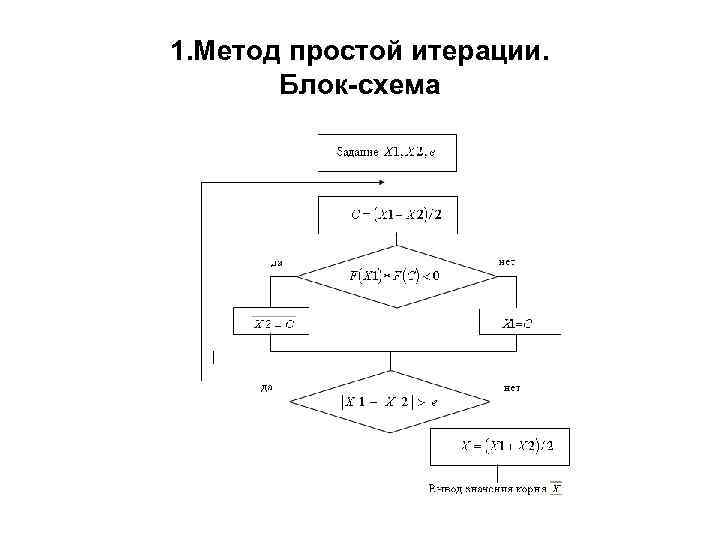
1. Метод простой итерации. Блок-схема
2. Метод половинного деления (дихотомии) Дано нелинейное алгебраическое уравнение вида f(x)=0. Требуется найти корни данного уравнения с точностью .
2. Метод половинного деления. Алгоритм 1 шаг. Приблизительно оценивают на каком отрезке находится корень уравнения. Для этого существуют 2 способа: Графический. а) Исходное уравнение, для удобства построения графиков функций, преобразуют к виду: f 1(x)=f 2(x). Например: x-cos(x)=0 x=cos(x), б) Строят графики функций у= f 1(x) и y=f 2(x) и находят точки их пересечения. Точек пересечения может быть несколько. Абсциссы этих мочек пересечения являются приближенными корнями исходного уравнения.
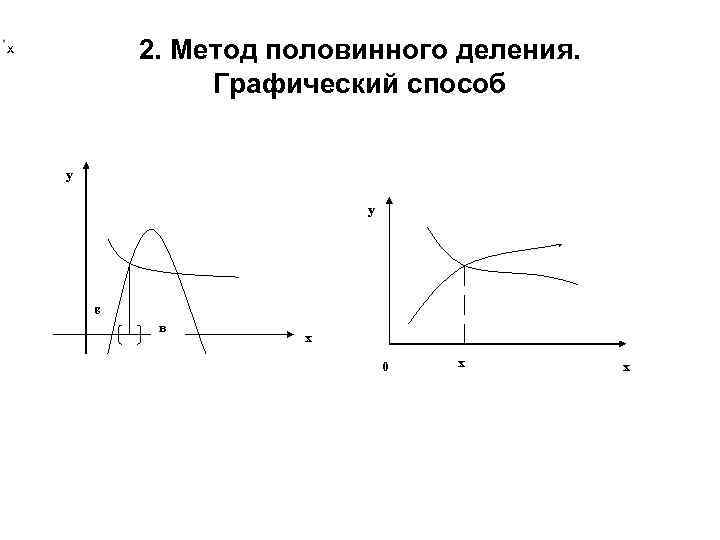
2. Метод половинного деления. Графический способ х у у в х 0 х х а
![2. Метод половинного деления. Графический и аналитический способ в) далее выбираем отрезок [a, в]](https://present5.com/presentation/157156096_427886391/image-15.jpg "2. Метод половинного деления. Графический и аналитический способ в) далее выбираем отрезок [a, в]")
2. Метод половинного деления. Графический и аналитический способ в) далее выбираем отрезок [a, в] содержащий тот единственных корень исходного уравнения, которых находится ближе к нулю (с той или иной стороны). При этом функция f(x) на концах отрезка будет иметь разные знаки, т. е. f(а)* f(в)<0. • Аналитический. Строят таблицу значений функции у= f(x), корень будет находится в том интервале, на концах которого функция имеет разные знаки. (Шаг брать 0. 1).
![2. Метод половинного деления. Алгоритм 2 шаг. Уточнение корня. а) Найденный отрезок [а, в]](https://present5.com/presentation/157156096_427886391/image-16.jpg "2. Метод половинного деления. Алгоритм 2 шаг. Уточнение корня. а) Найденный отрезок [а, в]")
2. Метод половинного деления. Алгоритм 2 шаг. Уточнение корня. а) Найденный отрезок [а, в] делят пополам, в точке с = (a+b)/2 вычисляют значение функции f(с). б) Точка с делит [а, в] на два отрезка: [а, с] и [с, в]. а с в
2. Метод половинного деления. Алгоритм 2 шаг. Корень находится в том интервале, на концах которого функция f(x) имеет разные знаки, т. е. f(a)*f(c)<0 f(a)*f(c)>0 f(в)* f(c)<0 корень на [а, с] либо корень на [в, с] Для дальнейшего уточнения выбирается отрезок, содержащий корень. Таким образом отрезок сужается вдвое.
2. Метод половинного деления. Алгоритм Например, f(a)>0 f(c)<0 f(в)>0 а х с в в) Полученный отрезок вновь делится пополам и т. д. г) Процесс повторяется до тех пор пока длина отрезка [a, в] не станет меньше , т. е. |а-в|< . Тогда процесс вычисления заканчивается и корень уравнения находится как х = (a+b)/2.
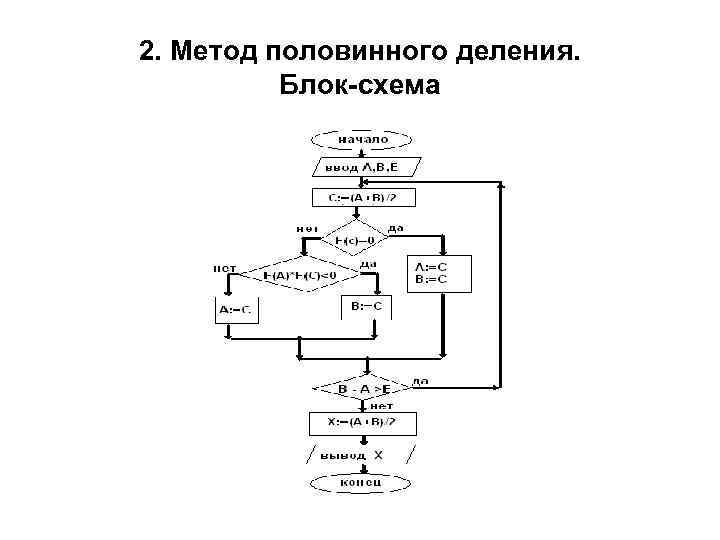
2. Метод половинного деления. Блок-схема
3. Метод Ньютона (метод касательных) Дано нелинейное алгебраическое уравнение вида f(x)=0. Требуется найти корни данного уравнения с точностью .
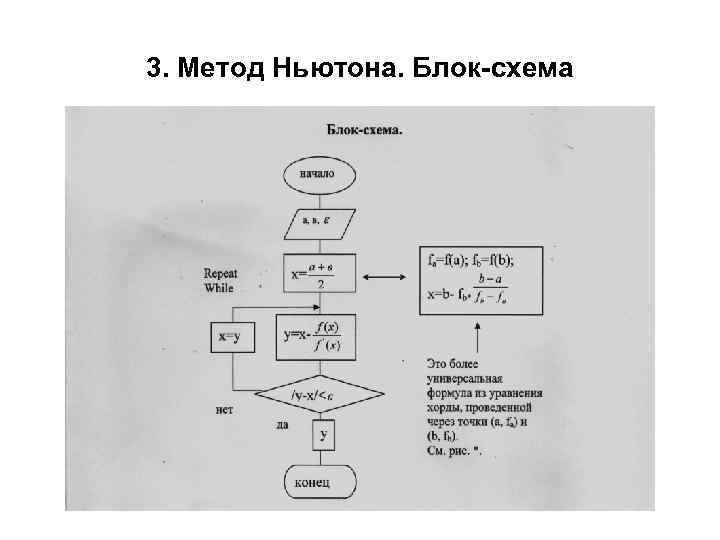
3. Метод Ньютона. Алгоритм 1 шаг. Выбирается отрезок на котором находится корень уравнения (см. метод половинного деления). 2 шаг. Уточнение корня. а) За начальное приближение берется любая точка отрезка [а, в]. Допустим середина
3. Метод Ньютона. Геометрический смысл метода х1 - ? tgα 0=f ’(x 0) (x 0 -x 1)*tg α 0= f(x 0) x 0 -x 1= x 1 =x 0 - .
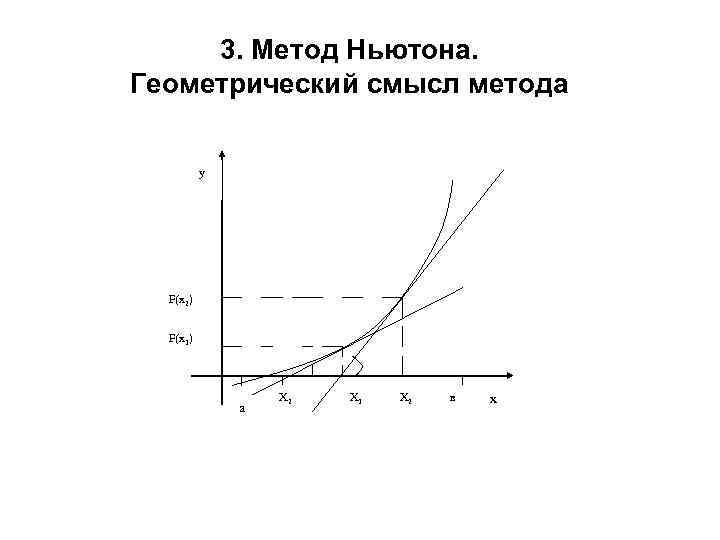
3. Метод Ньютона. Геометрический смысл метода у F(x 2) F(x 1) а Х 2 Х 1 Х 2 в х
3. Метод Ньютона. Алгоритм. 2 шаг • Проводим касательную к кривой у=f(x) в точке (х0 , f(x 0)). Пересечение касательной с осью (ох) обозначим за х1 – эта точка будет следующим приближением корня. • б) Далее проводим касательную к кривой у=f(x) в точке (х1, f(x 1)), ее пересечение с осью (ох) даст очередное приближение корня. И так далее. • в) Процесс продолжается до тех пор пока разница между очередным приближением и предыдущим не станет меньше ε.
3. Метод Ньютона. Аналитические выражения Из геометрических соотношений (из уравнения касательной) получаем что x 1 = x 0 xк+1 =xк- ; x 2 =x 1. ;
3. Метод Ньютона. Блок-схема
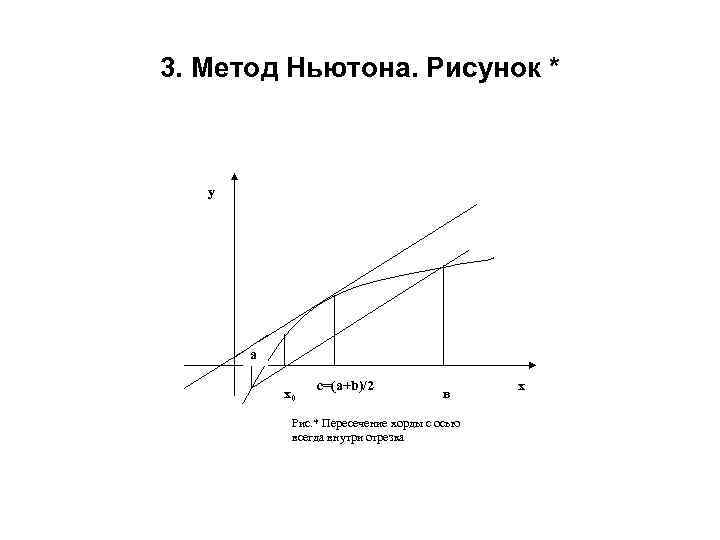
3. Метод Ньютона. Рисунок * у а х0 с=(a+b)/2 в Рис. * Пересечение хорды с осью всегда внутри отрезка х
4. Метод хорд. Дано нелинейное алгебраическое уравнение вида f(x)=0. Требуется найти корни данного уравнения с точностью .
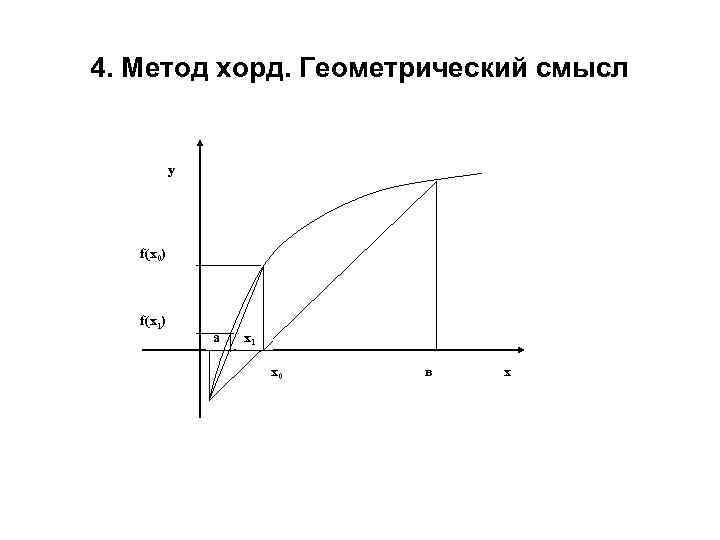
4. Метод хорд. Алгоритм 1 шаг. Выбирается отрезок, на котором находится корень уравнения (см. метод половинного деления). 2 шаг. Уточняется корень. а) В качестве начального приближения берётся точка х0=в-f(в)* - точка пересечения хорды (а, f(a)) и (в, f(в)) с осью (ох).
4. Метод хорд. Геометрический смысл у f(х0) f(х1) а х1 х0 в х
![4. Метод хорд. Алгоритм Далее из двух отрезков [а, х0] и [х0, в] выбирается](https://present5.com/presentation/157156096_427886391/image-31.jpg "4. Метод хорд. Алгоритм Далее из двух отрезков [а, х0] и [х0, в] выбирается")
4. Метод хорд. Алгоритм Далее из двух отрезков [а, х0] и [х0, в] выбирается тот на концах, которого функция f(x) имеет разные знаки. б) Вновь проводится хорда через концы нового отрезка – точка ее пересечения с осью (ох) является очередным приближением корня. в) Процесс продолжается до тех пор пока разница между очередным приближением и предыдущим не станет меньше , т. е. |хк+1 -хк|< .
d= 4. Метод хорд. Аналитические выражения Получим формулу для вычисления приближения хк. 1) Уравнение прямой проходящей через точку х: у(х)= dx+с. 2) Хорда проходит через две точки (а, f(a)) и (в, f(в)) имеет место система уравнений:
4. Метод хорд. Аналитические выражения 3)В точке пересечения хорды с осью (ох) имеем dx 0+c = 0 x 0= следовательно x 0=в-f(в)* либо x 0=а-f(а)*
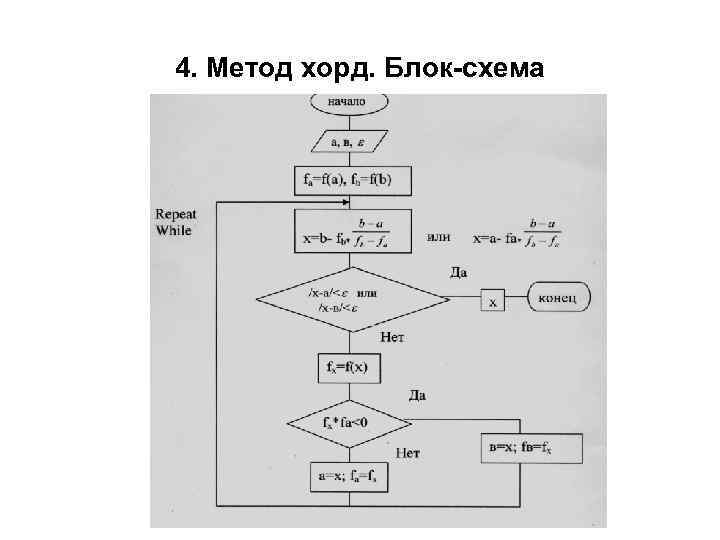
4. Метод хорд. Блок-схема
Скачать презентацию Приближенные методы решения нелинейных алгебраических уравнений План
Методы решения нелинейных алгебраических уравнений.ppt