Приближенное решение уравнений.ppt
- Количество слайдов: 67

Приближенное решение уравнений Преподаватель: Редькина Белла Александровна

Постановка задачи: n Рассмотрим решение нелинейных уравнений с одним неизвестным. n Число х* называется корнем уравнения или нулем функции если при подстановке его в уравнение, оно превращается в верное равенство.

n n n Решить уравнение – это значит найти множество всех его корней. Решать уравнения можно аналитическими и численными методами. При помощи численных методов можно получить решения уравнений, совершенно недоступных для аналитических методов.
Процесс приближенного решения уравнений Отделение корней Уточнение корней

n Решение задачи начинается с отделения корней. Отделить корни уравнения – значит для каждого из корней найти свой отрезок изоляции. n Поиск приближенного значения корня с точностью до заданного числа >0 называется уточнением этого корня.

Отделение корней n Графический способ отделения корней уравнений заключается в поиске таких отрезков [a; b], внутри которых находится абсцисса точки пересечения графика функции с осью Ох.
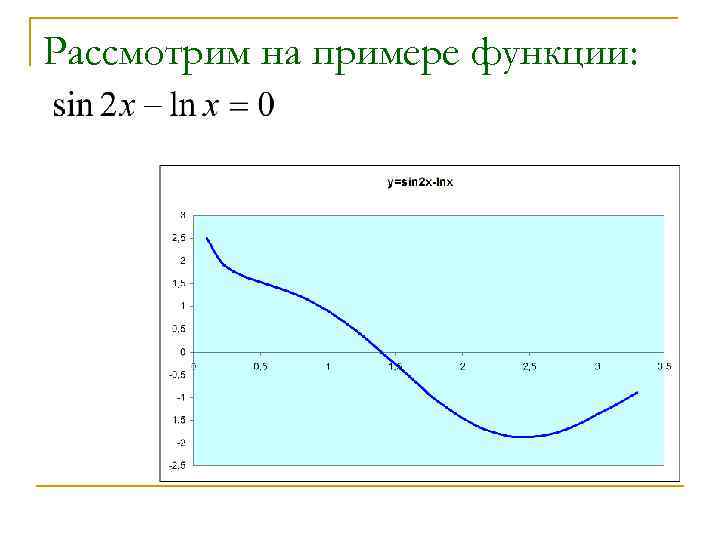
Рассмотрим на примере функции:

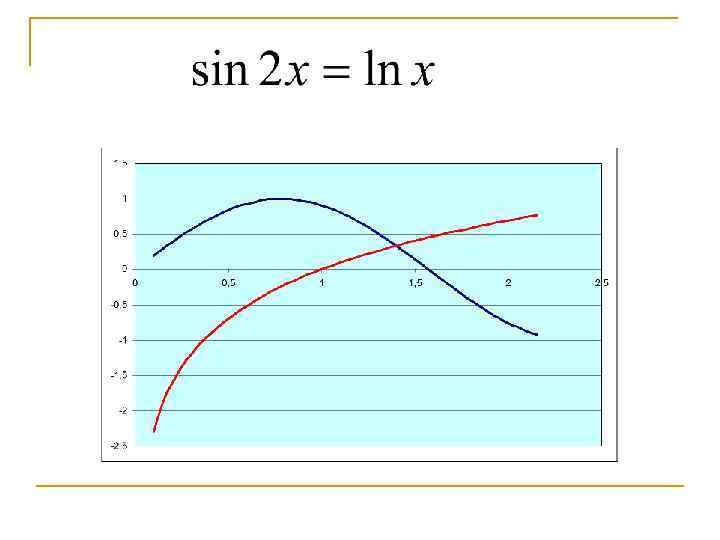
n Задачу можно упростить заменив исходное уравнение на равносильное: Строятся отдельные графики для и , потом, на оси х отмечаются отрезки на которых находится точка пересечения графиков.
![Отделение корней n n Если непрерывная на отрезке [a, b] функция принимает на его Отделение корней n n Если непрерывная на отрезке [a, b] функция принимает на его](https://present5.com/presentation/41393827_224114781/image-10.jpg)
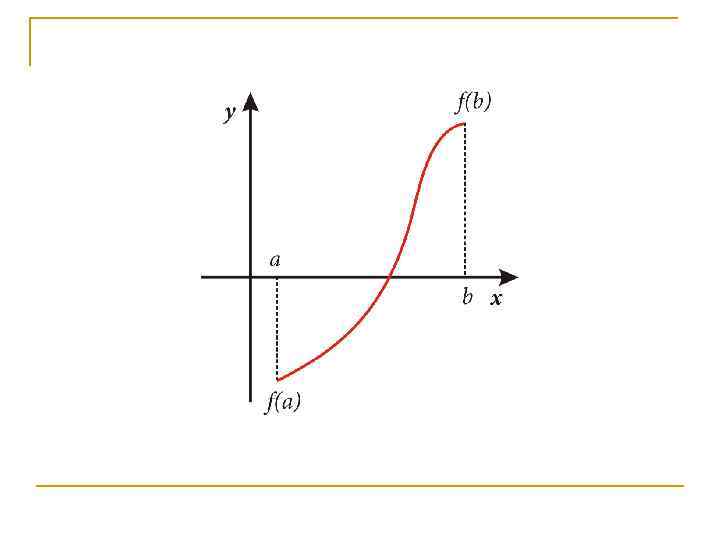
Отделение корней n n Если непрерывная на отрезке [a, b] функция принимает на его концах значения разных знаков, то уравнение имеет на этом отрезке по меньшей мере один корень. Если функция при этом монотонна, то этот корень единственный.
![n Пусть имеется уравнение и все корни находятся на отрезке [A; B], на котором n Пусть имеется уравнение и все корни находятся на отрезке [A; B], на котором](https://present5.com/presentation/41393827_224114781/image-11.jpg)
n Пусть имеется уравнение и все корни находятся на отрезке [A; B], на котором функция определена, непрерывна и на концах отрезка принимает разные знаки. Требуется отделить корни, т. е указать все отрезки , содержащие по одному корню.

n Будем вычислять значения функции начиная с точки А, двигаясь вправо с некоторым шагом h. Как только обнаружится пара соседних значений, имеющих разные знаки, и функция монотонна на данном отрезке, то можно считать этот отрезок, содержащим корень.
![Пример: n Рассмотрим отрезок [-3; 2] шаг h=1 х y -3 1, 049787 -2 Пример: n Рассмотрим отрезок [-3; 2] шаг h=1 х y -3 1, 049787 -2](https://present5.com/presentation/41393827_224114781/image-13.jpg)
Пример: n Рассмотрим отрезок [-3; 2] шаг h=1 х y -3 1, 049787 -2 0, 135335 -1 -0, 63212 0 -1 1 -0, 28172 2 3, 389056

Уточнение корней
![Метод половинного деления n Пусть уравнение имеет на отрезке [a; b] единственный корень. Функция Метод половинного деления n Пусть уравнение имеет на отрезке [a; b] единственный корень. Функция](https://present5.com/presentation/41393827_224114781/image-15.jpg)
Метод половинного деления n Пусть уравнение имеет на отрезке [a; b] единственный корень. Функция на отрезке непрерывна. Разделим отрезок пополам точкой с

n Если при этом случая: то возможны два n Выбирая тот отрезок, на котором функция меняет знак и отбрасывая оставшийся отрезок, мы продолжаем метод половинного деления.
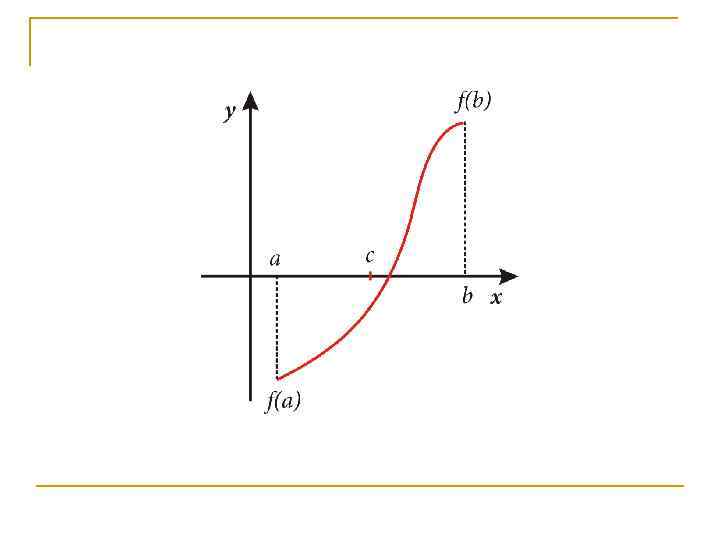
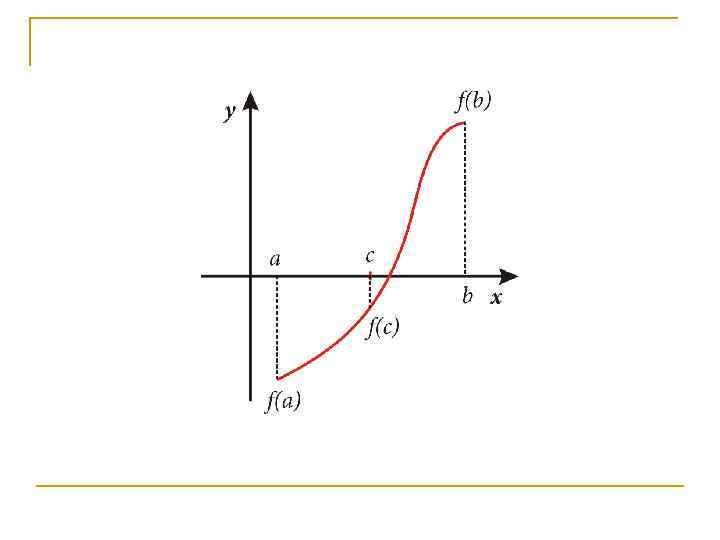
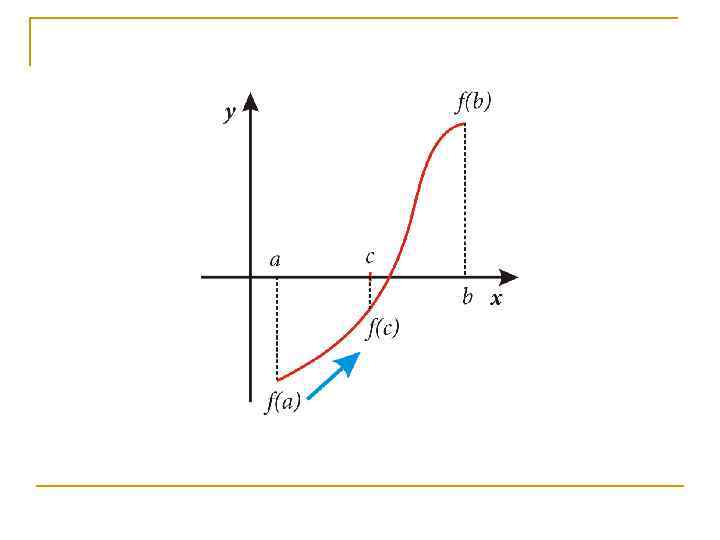
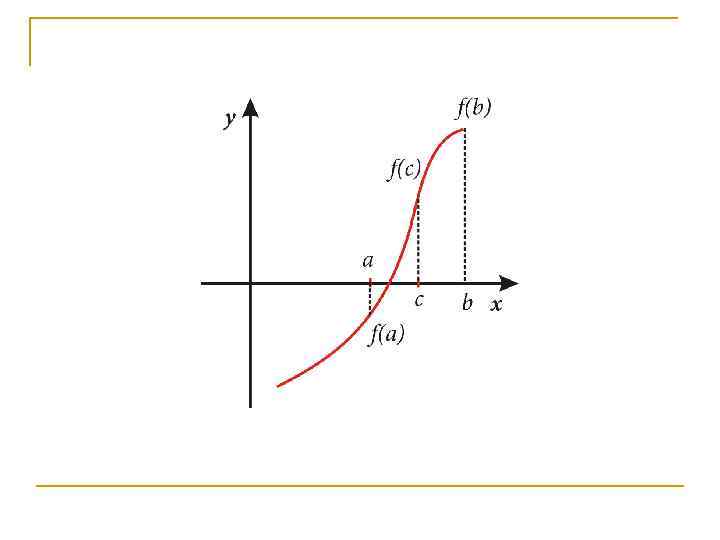

n Для того чтобы найти приближенное значение корня с точностью до >0, необходимо остановить процесс половинного деления на таком шаге n, на котором отрезок [a; b] будет иметь длину
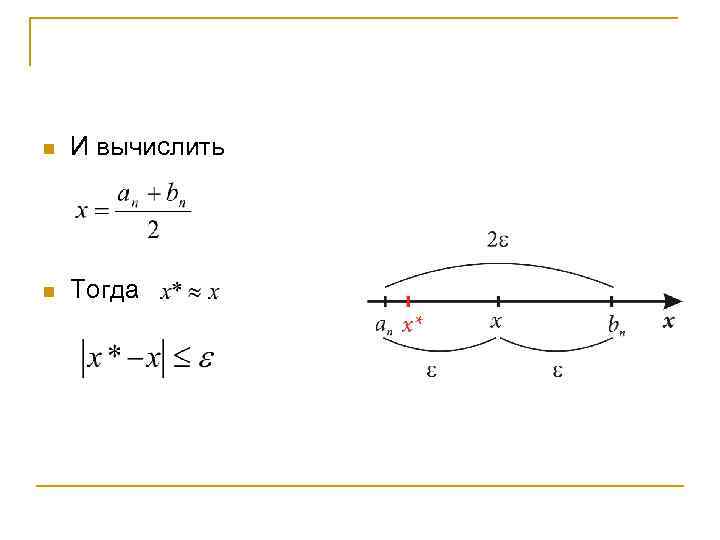
n И вычислить n Тогда

Пример n Дано уравнение n Необходимо найти корень уравнения с точностью
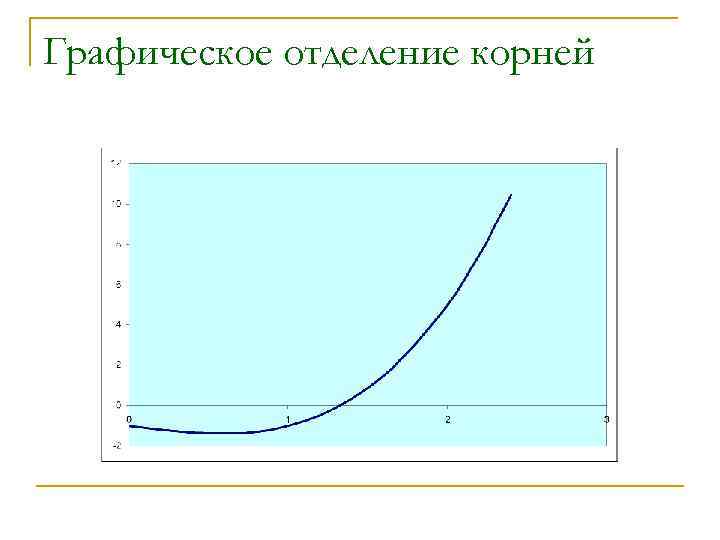
Графическое отделение корней
![n Единственный корень уравнения расположен на отрезке [1; 2] n Единственный корень уравнения расположен на отрезке [1; 2]](https://present5.com/presentation/41393827_224114781/image-26.jpg)
n Единственный корень уравнения расположен на отрезке [1; 2]

n Для уточнения корня уравнения можно применить метод половинного деления, поскольку функция непрерывна на этом отрезке и на его концах принимает разные знаки:
![1. 2. 3. 4. 5. Найдем середину с=1, 5 отрезка [1; 2] Вычислим значение 1. 2. 3. 4. 5. Найдем середину с=1, 5 отрезка [1; 2] Вычислим значение](https://present5.com/presentation/41393827_224114781/image-28.jpg)
1. 2. 3. 4. 5. Найдем середину с=1, 5 отрезка [1; 2] Вычислим значение функции в этой точке Значит, число 1, 5 не является точным корнем уравнения. Далее проверяем: Следовательно корень уравнения находится на отрезке [1; 1, 5]

n n Делим полученный отрезок точкой и находим Необходимая точность вычисления не достигнута. Проверяем дальше: Следовательно корень уравнения находится на отрезке [1, 25; 1, 5]. И так продолжается до достижения необходимой точности двух верных цифр после запятой.

Метод хорд и метод касательных

n n Эти методы относятся к методам последовательных приближений. Приближение к корню находится так: q n если известно предыдущее приближение xn , то последующее приближение xn+1 вычисляется по формуле: Где Р – некоторое выражение, устанавливающее связь между предыдущим и последующим приближениями.
![Метод касательных n Пусть дано уравнение , корень которого отделен на отрезке [a; b], Метод касательных n Пусть дано уравнение , корень которого отделен на отрезке [a; b],](https://present5.com/presentation/41393827_224114781/image-32.jpg)
Метод касательных n Пусть дано уравнение , корень которого отделен на отрезке [a; b], кроме того на отрезке функция имеет непрерывные первую и вторую производные, сохраняющие знак при всех
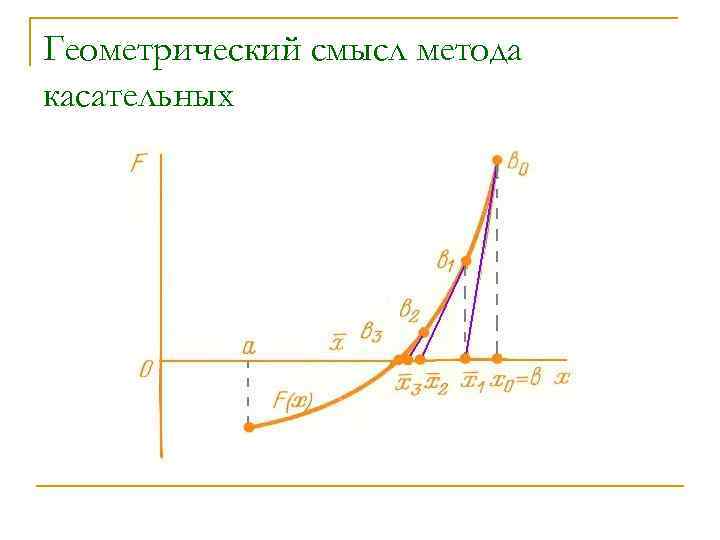
Геометрический смысл метода касательных

n За нулевое приближение берется тот конец отрезка, на котором функция и ее вторая производная имеют одинаковые знаки, т. е. выполняется условие n Процесс уточнения корня заканчивается когда f(x)<
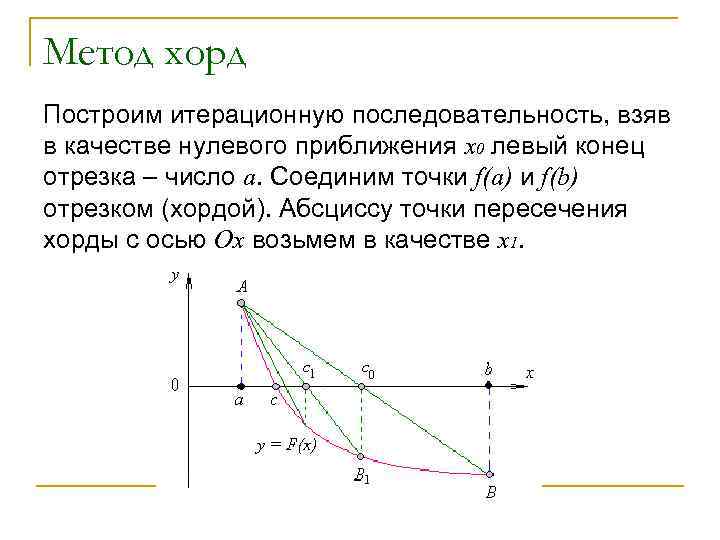
Метод хорд Построим итерационную последовательность, взяв в качестве нулевого приближения х0 левый конец отрезка – число а. Соединим точки f(a) и f(b) отрезком (хордой). Абсциссу точки пересечения хорды с осью Ох возьмем в качестве х1.

n Уравнение хорды n Положив в этом уравнении y=0 получим x=x Следовательно n 1 n Продолжаю итерационную последовательность получим: n Процесс продолжаем до тех пор, пока не начнет выполняться условие |хn - хn-1 | < .

Численное интегрирование

Задача приближенного вычисления определенных интегралов n n n Интеграл от некоторой интегрируемой на отрезке [a; b] функции f. Далее всегда будем считать a<b. При a=b интеграл равен нулю.
![Постановка задачи n n n Когда f непрерывна на [a; b], для нее существует Постановка задачи n n n Когда f непрерывна на [a; b], для нее существует](https://present5.com/presentation/41393827_224114781/image-39.jpg)
Постановка задачи n n n Когда f непрерывна на [a; b], для нее существует первообразная F (F’(x)=f(x) для всех x [a; b]), причем Формула Ньютона-Лейбница, представляет точный метод вычисления определенного интеграла.
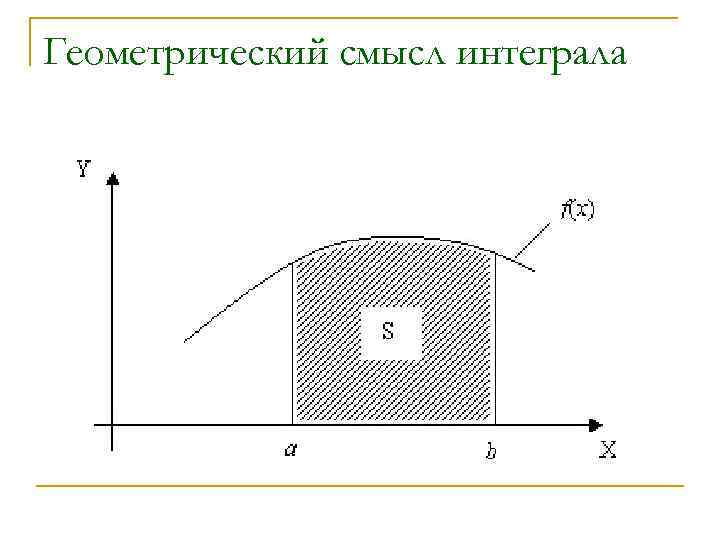
Геометрический смысл интеграла

n Формула Ньютона-Лейбница теряет практический смысл в случае неберущихся интегралов, если отыскание первообразной требует сложной процедуры или интеграл берется от табличной функции.

Приближенные методы интегрирования n Аналитические q Суть методов состоит в замене подынтегральной функции f на отрезке [a; b] некоторой аналитически заданной функцией p, чью первообразную нетрудно найти. Тогда имеет место формула:

Численные методы интегрирования n n Приближение к интегралу отыскивается по числовому выражению на основе значений подынтегральной функции в конечном множестве точек из отрезка интегрирования. Такой способ вычисления называется механической квадратурой.

n Приближенные формулы называют формулами численного интегрирования или квадратурными формулами, а используемые при этом аргументы функции – узлами квадратуры.
![Численное интегрирование n Разделим отрезок интегрирования [a; b] на n равных частей одинаковой длины Численное интегрирование n Разделим отрезок интегрирования [a; b] на n равных частей одинаковой длины](https://present5.com/presentation/41393827_224114781/image-45.jpg)
Численное интегрирование n Разделим отрезок интегрирования [a; b] на n равных частей одинаковой длины n h – шаг интегрирования
![Формулы прямоугольников n Интегрируемость функции f на отрезке [a; b] означает, что если отрезок Формулы прямоугольников n Интегрируемость функции f на отрезке [a; b] означает, что если отрезок](https://present5.com/presentation/41393827_224114781/image-46.jpg)
Формулы прямоугольников n Интегрируемость функции f на отрезке [a; b] означает, что если отрезок разбить точками a=x 0<x 1<x 2<…<xn=b на n частей, выбрать ti [xi-1; xi] и составить интегральные суммы

Формулы прямоугольников n При h→ 0 , будет существовать конечный предел этих сумм, не зависящий ни от способа разбиения отрезка на части, ни от выбора точек ti из этих частей. Этот предел и есть определенный интеграл

Формулы прямоугольников n n Поскольку способ разбиения отрезка может быть любым, в дальнейшем всегда будем разбивать его на равные части, а при h→ 0, что равносильно Следовательно можно положить
![Формула левых прямоугольников n Если взять ti равными левым концам отрезков [xi-1; xi], yi-1=f(xi-1), Формула левых прямоугольников n Если взять ti равными левым концам отрезков [xi-1; xi], yi-1=f(xi-1),](https://present5.com/presentation/41393827_224114781/image-49.jpg)
Формула левых прямоугольников n Если взять ti равными левым концам отрезков [xi-1; xi], yi-1=f(xi-1), то получим: n Формулу прямоугольников с левыми ординатами
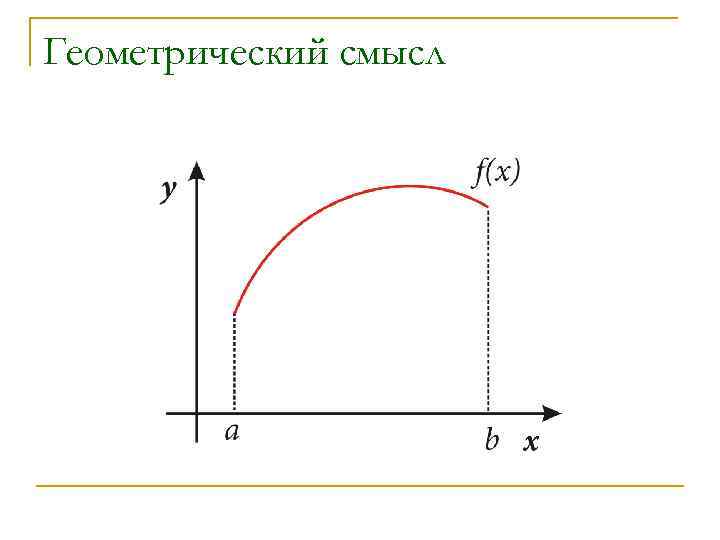
Геометрический смысл
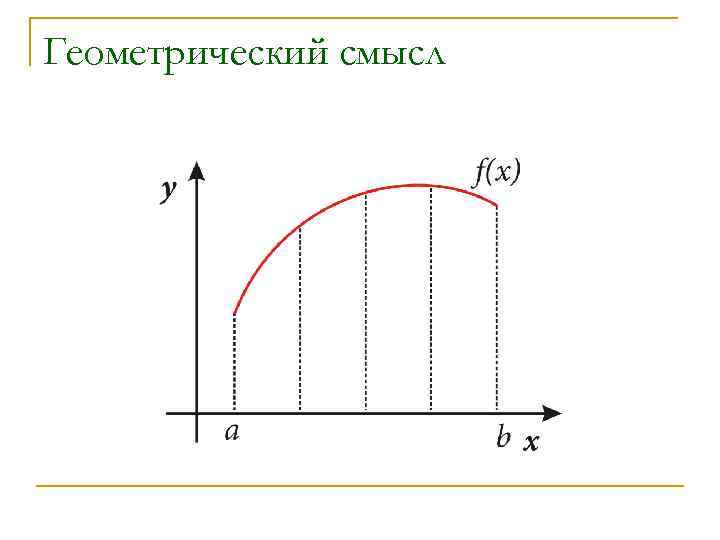
Геометрический смысл
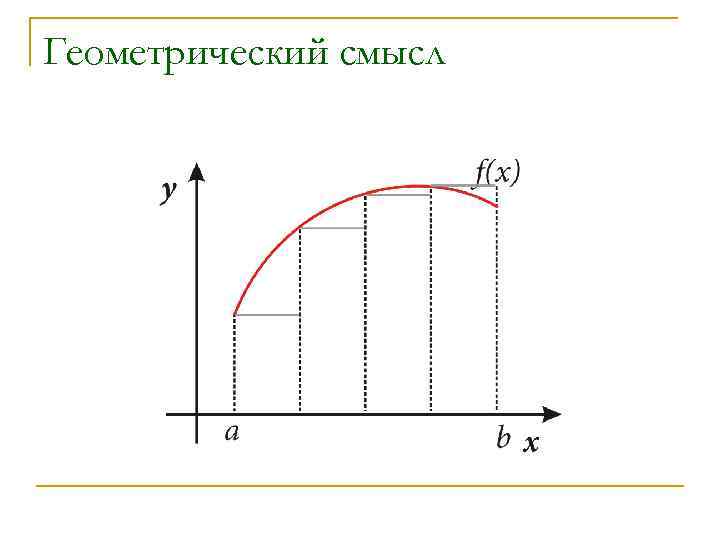
Геометрический смысл
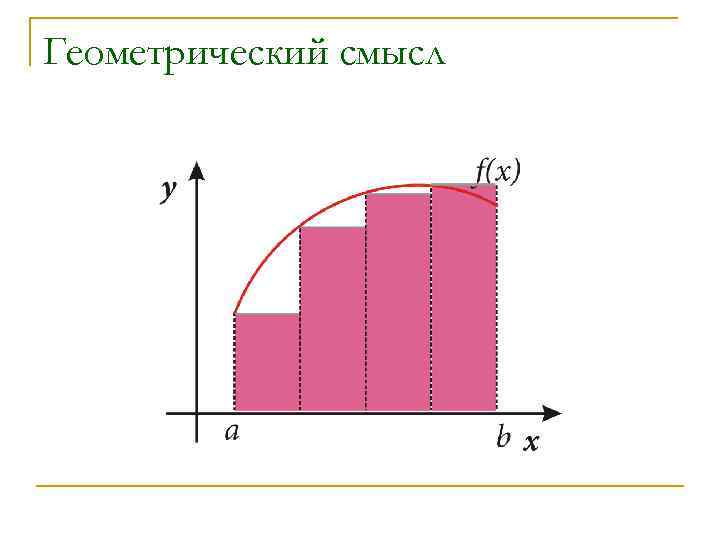
Геометрический смысл
![Формула правых прямоугольников n Если взять ti равными правым концам отрезков [xi-1; xi], yi=f(xi), Формула правых прямоугольников n Если взять ti равными правым концам отрезков [xi-1; xi], yi=f(xi),](https://present5.com/presentation/41393827_224114781/image-54.jpg)
Формула правых прямоугольников n Если взять ti равными правым концам отрезков [xi-1; xi], yi=f(xi), то получим: n Формулу прямоугольников с правыми ординатами
Геометрический смысл
Геометрический смысл
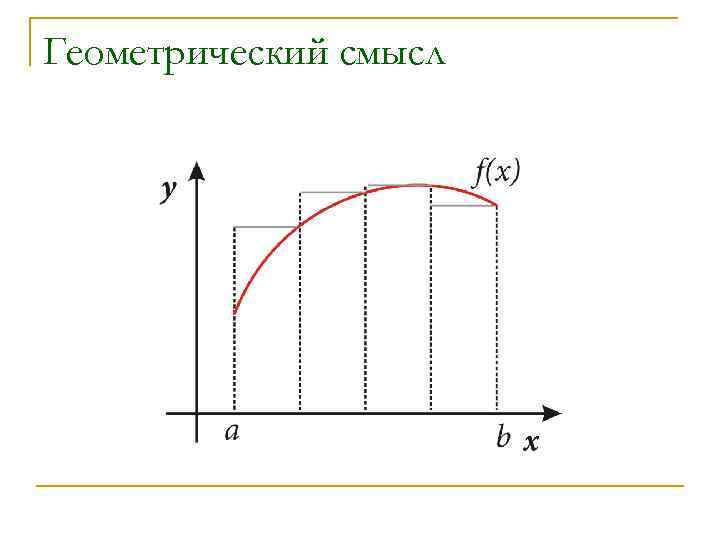
Геометрический смысл
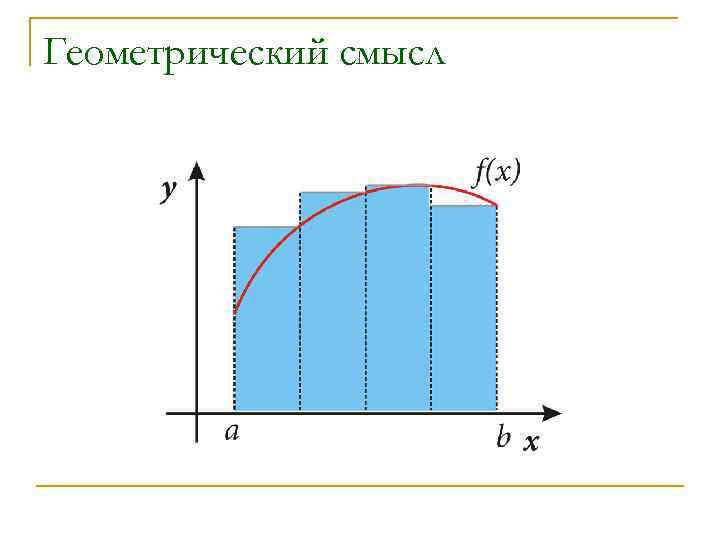
Геометрический смысл
![Метод трапеций n Разобъем отрезок [a; b] точками a=x 0<x 1<x 2<…<xn=b на n Метод трапеций n Разобъем отрезок [a; b] точками a=x 0<x 1<x 2<…<xn=b на n](https://present5.com/presentation/41393827_224114781/image-59.jpg)
Метод трапеций n Разобъем отрезок [a; b] точками a=x 0<x 1<x 2<…<xn=b на n частей n На каждом из отрезков [xi-1; xi] функцию f заменим по формуле линейного интерполирования
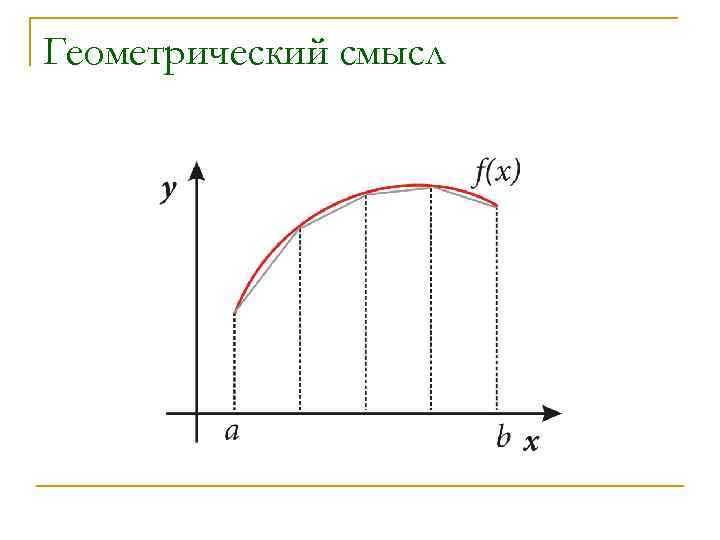
Геометрический смысл
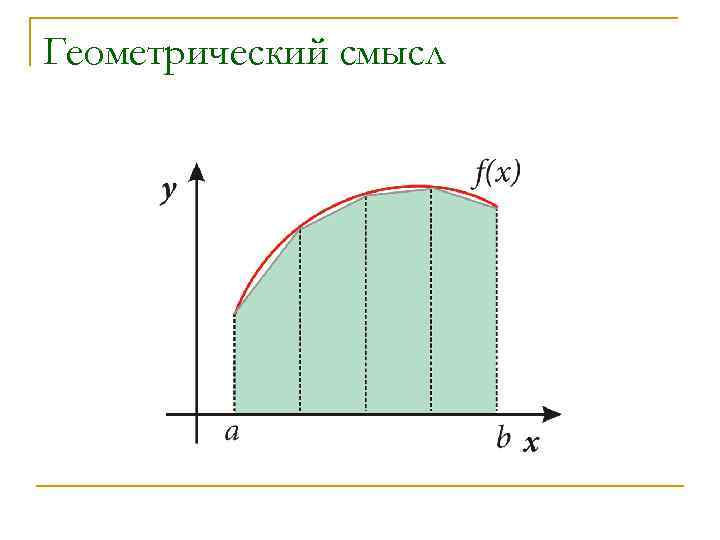
Геометрический смысл

Метод трапеций n n Вычисление интеграла сводится к вычислению площадей трапеций. Площадь трапеции вычисляется по формуле:

Формула трапеций n На всем отрезке интегрирования получим формулу:

Погрешность численного интегрирования n n У погрешности численного интегрирования два источника: это погрешность квадратурных формул Vn и погрешность вычислений vn Абсолютная погрешность приближенного интеграла определяется по формуле: n Jn=Vn+vn

Контрольная работа Вариант 15 n n f(x) a 0, 1 b 1, 1 Вычислить интеграл от заданной функции методом прямоугольников и методом трапеций при разбиении отрезка интегрирования на 10 частей. Вычисления проводятся с точностью <0, 0005

Задания к зачету: Вариант 13 n n Уравнение Отделить корни уравнения любым способом (аналитическим или графическим). Определить интервалы, где содержатся корни и уточнить их методом половинного деления с точностью <0, 0005

Структура контрольной работы 1 • Автор 2 • Вариант 3 • Условия задачи 4 • Описание хода решения 5 • Блок-схема 6 • Программа (соотнести с блок-схемой) 7 • Результаты 8 • Объяснение результатов
Приближенное решение уравнений.ppt