Приближение функций
Пример. Получить приближение функции f(x) для аргумента x=1, 5 методом Лагранжа. x y Х 0 Y 0 0 0 Х 1 Y 1 1 1 Х 2 Y 2 2 4 Х 3 Y 3 3 9
x y Х 0 Y 0 0 0 Х 1 Y 1 1 1 Х 2 Y 2 2 4 Х 3 Y 3 3 9
![Пример. Необходимо оценить погрешность приближения f(x)= x в точке x=116 на отрезке [a, b],](https://present5.com/presentation/15751739_91860122/image-4.jpg "Пример. Необходимо оценить погрешность приближения f(x)= x в точке x=116 на отрезке [a, b],")
Пример. Необходимо оценить погрешность приближения f(x)= x в точке x=116 на отрезке [a, b], где a=100, b=144 с помощью интерполяционного многочлена Лагранжа L 2(X), построенного с узлами X 0=100, X 1=121, X 2=144.
Решение. Так как n=2, необходимо найти максимальное значения производной 3 го порядка функции f(x)=x½. Производные заданной функции до третьего порядка включительно: Функция f (X) на отрезке [100, 144] принимает максимальное значение в точке Х=100:
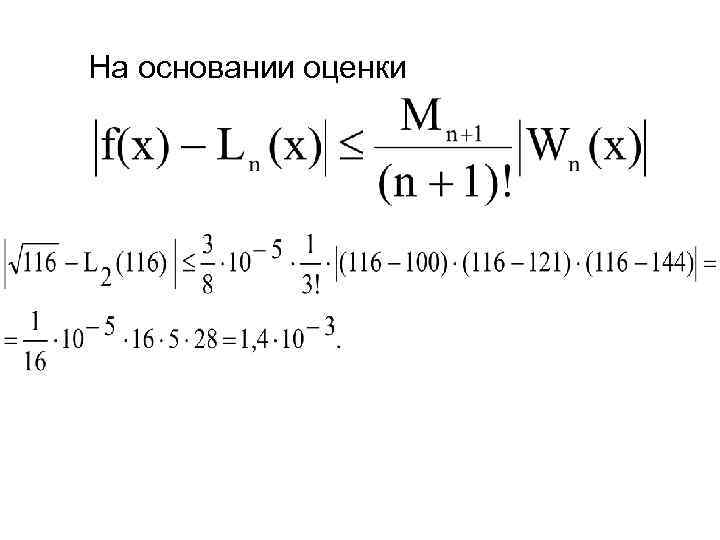
На основании оценки
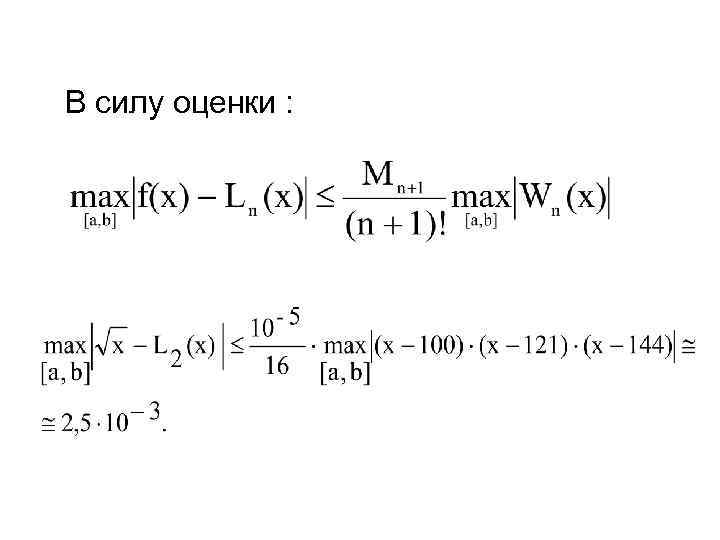
В силу оценки :
Геометрическая интерпретация приближения функции с использованием аппроксимирующего многочлена y Результаты измерений yn y 0 Х 0 Х 1 Х 2 Хn Х
Геометрическая интерпретация приближения функции с использованием аппроксимирующего многочлена f(Х) –истинное поведение функции y yn y 0 Х 0 Х 1 Х 2 Хn Х
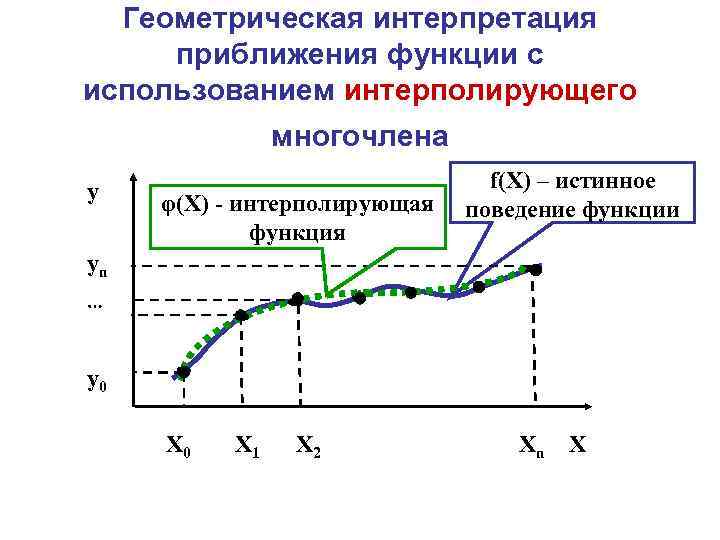
Геометрическая интерпретация приближения функции с использованием интерполирующего многочлена y φ(Х) - интерполирующая функция f(Х) – истинное поведение функции yn y 0 Х 0 Х 1 Х 2 Хn Х
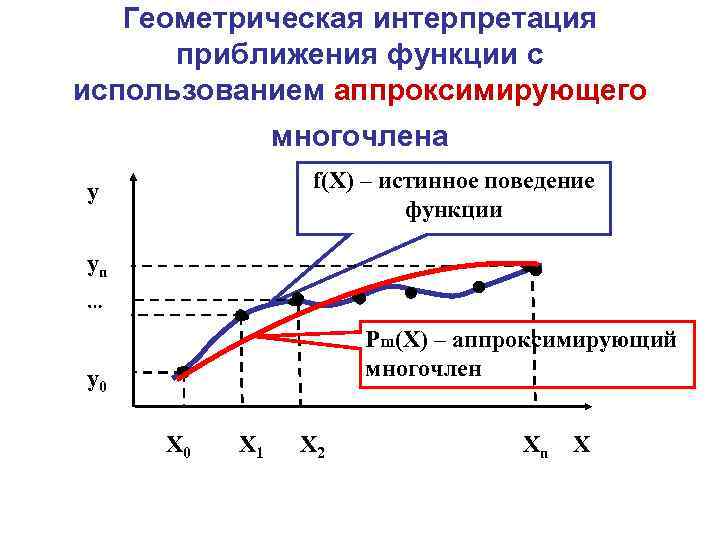
Геометрическая интерпретация приближения функции с использованием аппроксимирующего многочлена f(Х) – истинное поведение функции y yn Рm(Х) – аппроксимирующий многочлен y 0 Х 0 Х 1 Х 2 Хn Х
Численное интегрирование
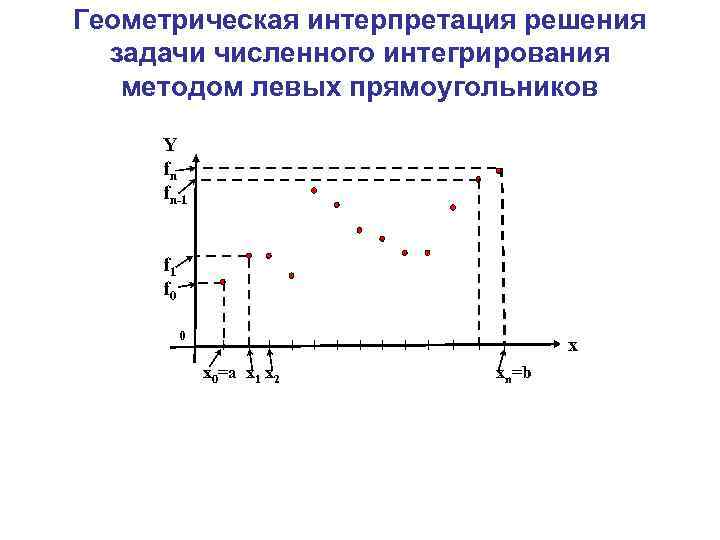
Геометрическая интерпретация решения задачи численного интегрирования методом левых прямоугольников Y fn fn-1 А 1 f 0 А 0 0 x x 0=a x 1 x 2 xn=b
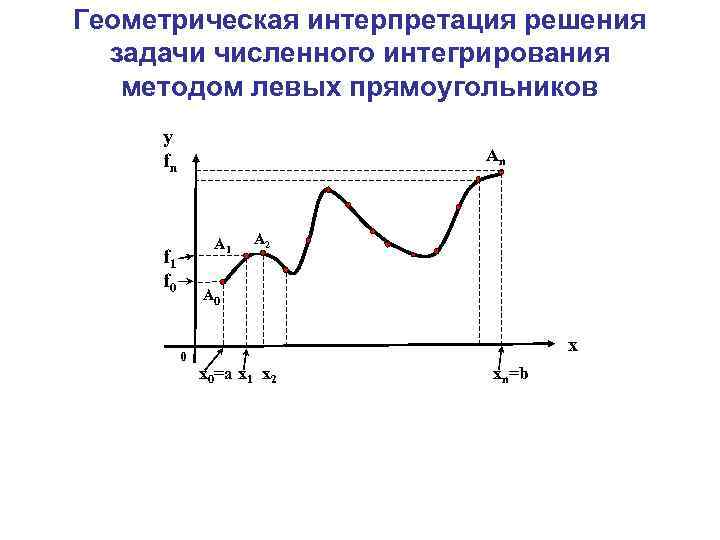
Геометрическая интерпретация решения задачи численного интегрирования методом левых прямоугольников y fn Аn А 1 f 0 А 2 А 0 0 x x 0=a x 1 x 2 xn=b
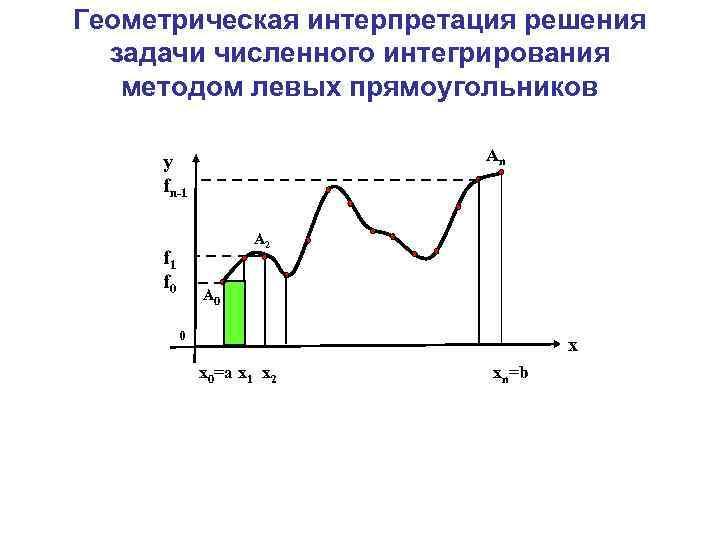
Геометрическая интерпретация решения задачи численного интегрирования методом левых прямоугольников Аn y fn-1 А 1 f 0 А 2 А 0 0 x x 0=a x 1 x 2 xn=b
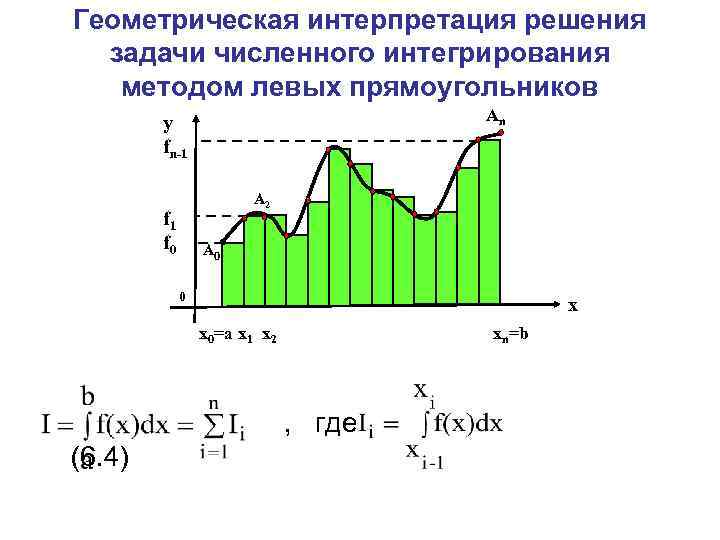
Геометрическая интерпретация решения задачи численного интегрирования методом левых прямоугольников Аn y fn-1 А 1 f 0 А 2 А 0 0 x x 0=a x 1 x 2 xn=b , где (6. 4)
Принимаемые обозначения fi=f(хi) значение подынтегральной функции в узле интегрирования, хi-½ = середины частичных отрезков [хi – хi-1], fi-½ = f(хi-½) значение функции для середины частичного отрезка [xi-1, xi], hi = хi – хi-1 длины частичных отрезков. Обычно шаг интегрирования h величина постоянная, т. е. hi=h=const.
Квадратурная формула для метода левых прямоугольников: (6. 5)
Пример 1. Получить численное значение определённого интеграла по формуле левых прямоугольников если подынтегральная функция задана таблицей (h=1): i 0 1 2 3 4 x f(x)=fi -1 1 0 0 1 1 2 4 3 9 Точное значение интеграла
h=0, 5 i 0 1 2 3 4 5 6 7 8 x f(x)=fi -1 1 -0, 5 0, 25 0 0 0, 5 0, 25 1 1 1, 5 2, 25 2 4 2, 5 6, 25 3 9 Точное значение интеграла
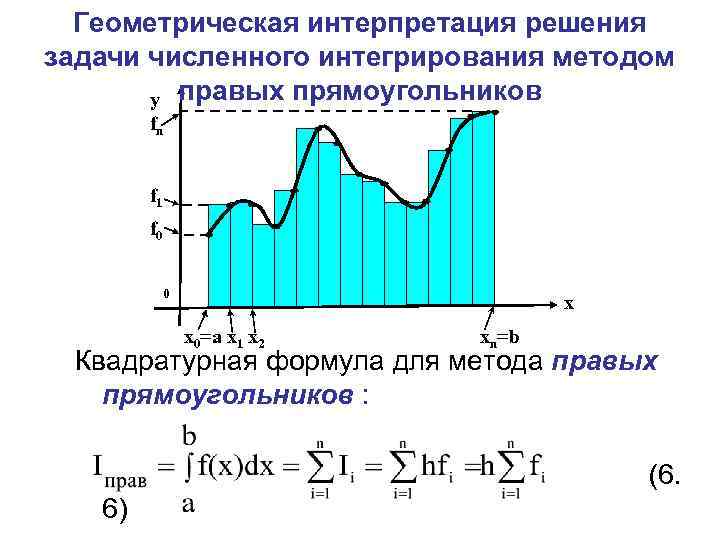
Геометрическая интерпретация решения задачи численного интегрирования методом y правых прямоугольников fn f 1 f 0 0 x x 0=a x 1 x 2 xn=b Квадратурная формула для метода правых прямоугольников : (6. 6)
Пример 2. Получить численное значение определённого интеграла по формуле правых прямоугольников если подынтегральная функция задана таблицей (h=1): i 0 1 2 3 4 x f(x)=fi -1 1 0 0 1 1 2 4 3 9 Точное значение интеграла
h=0, 5 i 0 1 2 3 4 5 6 7 8 x f(x)=fi -1 1 -0, 5 0, 25 0 0 0, 5 0, 25 1 1 1, 5 2, 25 2 4 2, 5 6, 25 3 9 Точное значение интеграла
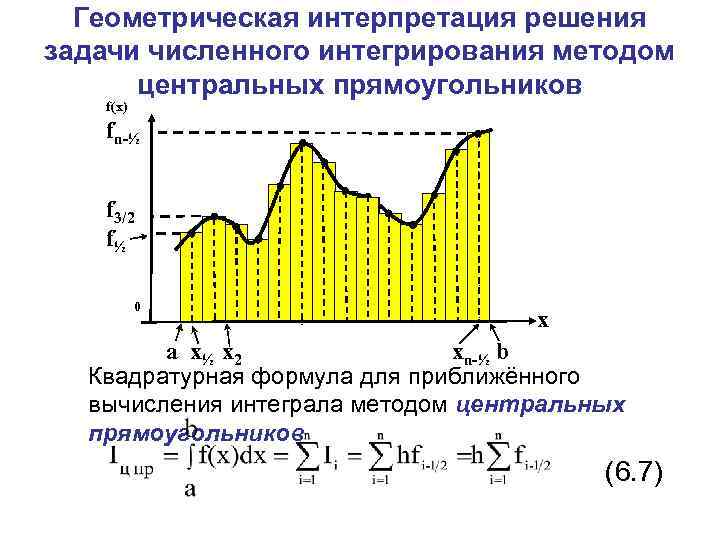
Геометрическая интерпретация решения задачи численного интегрирования методом центральных прямоугольников f(x) fn-½ f 3/2 f½ 0 x a x½ x 2 xn-½ b Квадратурная формула для приближённого вычисления интеграла методом центральных прямоугольников (6. 7)
Пример 3. Получить численное значение определённого интеграла по формуле центральных прямоугольников если подынтегральная функция задана таблицей (h=1): i 0 1 2 3 4 x f(x)=fi -1 1 0 0 1 1 2 4 3 9
h=0, 5 i 0 1 2 3 4 5 6 7 8 x f(x)=fi -1 1 -0, 5 0, 25 0 0 0, 5 0, 25 1 1 1, 5 2, 25 2 4 2, 5 6, 25 3 9
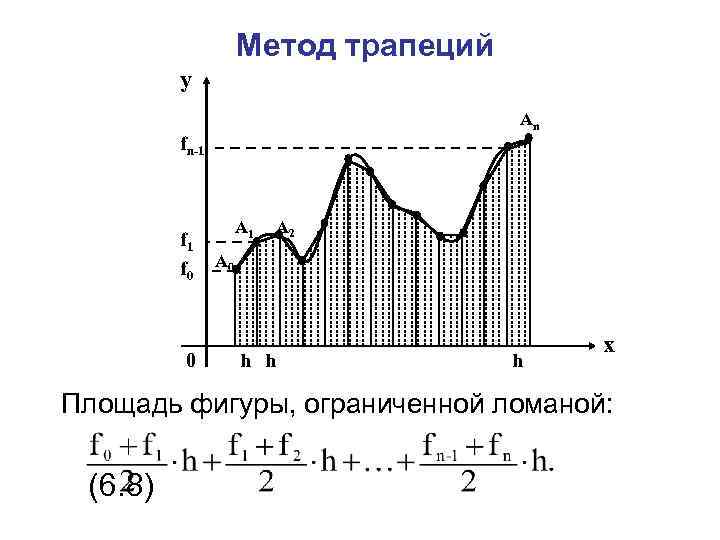
Метод трапеций y Аn fn-1 f 0 0 А 1 А 2 А 0 h h h x Площадь фигуры, ограниченной ломаной: (6. 8)
Формула трапеций:
Пример 4. Получить численное значение определённого интеграла по формуле трапеций, если подынтегральная функция задана таблицей (h=1): i 0 1 2 3 4 x f(x)=fi -1 1 0 0 1 1 2 4 3 9
h=0, 5 i 0 1 2 3 4 5 6 7 8 x f(x)=fi -1 1 -0, 5 0, 25 0 0 0, 5 0, 25 1 1 1, 5 2, 25 2 4 2, 5 6, 25 3 9 Точное значение интеграла
![Формула Симпсона На частичных отрезках [хi-1, хi+1] (i=1, …, n) подынтегральная функция f(х) приближается](https://present5.com/presentation/15751739_91860122/image-31.jpg "Формула Симпсона На частичных отрезках [хi-1, хi+1] (i=1, …, n) подынтегральная функция f(х) приближается")
Формула Симпсона На частичных отрезках [хi-1, хi+1] (i=1, …, n) подынтегральная функция f(х) приближается интерполяционным многочленом Лагранжа второго порядка. Для частичного отрезка [х0, х2] такой многочлен : (6. 14)
![Геометрическая интерпретация квадратичной интерполяции подынтегральной функции для частичного отрезка [хi-1, хi+1]. y Mi fi](https://present5.com/presentation/15751739_91860122/image-32.jpg "Геометрическая интерпретация квадратичной интерполяции подынтегральной функции для частичного отрезка [хi-1, хi+1]. y Mi fi")
Геометрическая интерпретация квадратичной интерполяции подынтегральной функции для частичного отрезка [хi-1, хi+1]. y Mi fi fi-1 Mi- fi+1 1 0 y=L 2(x) Mi+1 xi-1 xi xi+1 y=f(x) x
Из математического анализа известно: Площадь криволинейной трапеции, ограниченной параболой с осью, параллельной оси Оy (т. е. графиком квадратного трёхчлена y=Аx 2+Bx+C), равна произведению основания этой трапеции на сумму крайних ординат (ул и уп) и учетверённой средней ординаты параболы (ус): (6. 15)
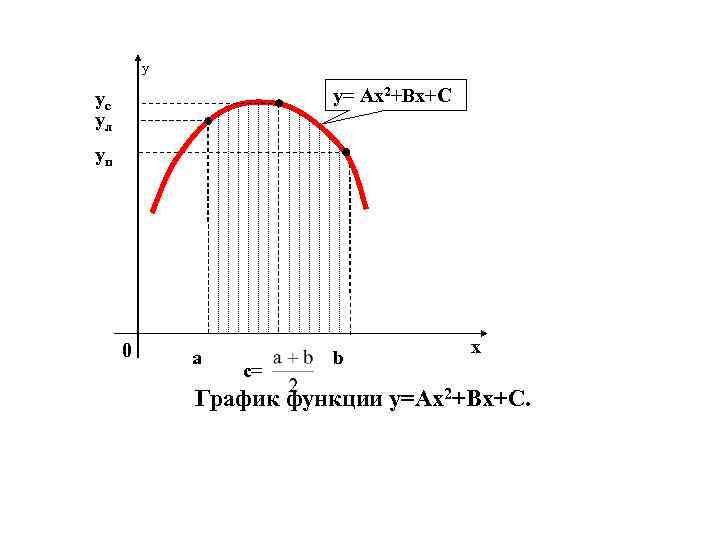
y y= Аx 2+Bx+C ус ул уп 0 a c= b x График функции у=Аx 2+Bx+C.
![Рассмотрим решение поставленной задачи для отрезка интегрирования произвольной длины. Заданный отрезок [a, b] разделим](https://present5.com/presentation/15751739_91860122/image-35.jpg "Рассмотрим решение поставленной задачи для отрезка интегрирования произвольной длины. Заданный отрезок [a, b] разделим")
Рассмотрим решение поставленной задачи для отрезка интегрирования произвольной длины. Заданный отрезок [a, b] разделим на чётное число (2 n) равных отрезков точками x 1, x 2, …, x 2 n-1. Длина каждого частичного отрезка равна Точки деления определяются формулами: x 1=a+h, x 2=a+2 h, …, xk=a+kh, …. Объединяя построенные отрезки попарно, будем рассматривать отрезки удвоенной длины : [x 0, x 2], [x 2, x 4], …, [x 2 n-2, x 2 n], x 0=а, x 2 n=b. Значения функции в точках x 0, x 1, x 2, … обозначим f 0, f 1, f 2, …, соответственно.
К каждому из членов этой суммы применим формулу (6. 15) и получим:
Формула Симпсона или формула парабол
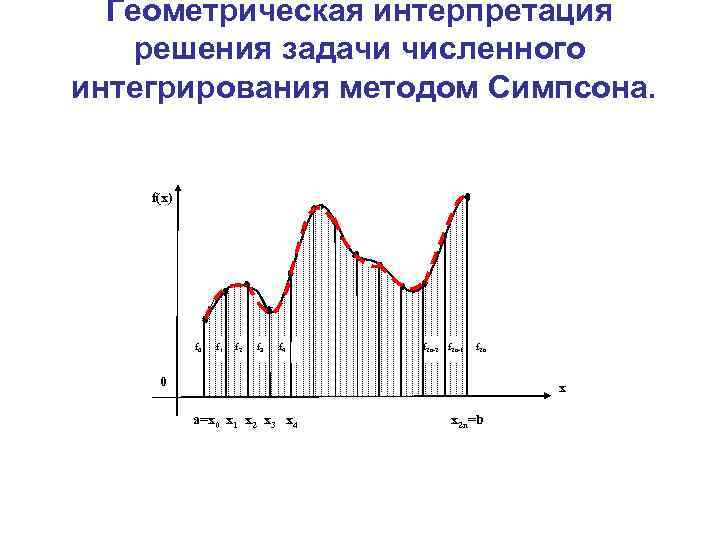
Геометрическая интерпретация решения задачи численного интегрирования методом Симпсона. f(x) f 0 f 1 f 2 f 3 f 4 f 2 n-2 f 2 n-1 f 2 n 0 x a=x 0 x 1 x 2 x 3 x 4 x 2 n=b
Формула Гаусса для численного интегрирования
Задача. При заданном числе N+1 узлов построить квадратурную формулу, точную для многочленов наиболее высокой степени. Формулы, удовлетворяющие этому условию, называются квадратурными формулами Гаусса. Сначала строят формулы Гаусса (1) для стандартного отрезка [-1, 1].
![Откажемся от равномерного распределения узлов xi на промежутке интегрирования [a, b]. Сделаем линейную замену](https://present5.com/presentation/15751739_91860122/image-41.jpg "Откажемся от равномерного распределения узлов xi на промежутке интегрирования [a, b]. Сделаем линейную замену")
Откажемся от равномерного распределения узлов xi на промежутке интегрирования [a, b]. Сделаем линейную замену переменной и преобразуем исходный интеграл к интегралу со стандартным промежутком интегрирования [ 1, 1]: (2)
Формула (1) точна для многочленов степени m тогда и только тогда, когда она точна для функций f(t) = 1, t, t 2, . . . , tm. Это эквивалентно тому, что узлы ti и веса Ai в (1) должны удовлетворять системе нелинейных уравнений k = 0, 1, . . . , m. (3) Система (3) имеет единственное решение A 0, A 1, . . . An, t 0, t 1, . . . tn (ti [-1, 1]) тогда и только тогда, когда число уравнений системы совпадает с числом неизвестных, т. е. m = 2 N + 1.
Пример. Построим функцию Гаусса с двумя узлами. В этом случае N =1, m = 3. Система (3) примет вид: (4)
Решая систему (4), получим: A 0 =A 1 =1; t 0 =-1/ , t 1 =1/. Т. о. получаем квадратурную формулу Гауссa, Для квадратурной формулы Гаусса справедлива следующая оценка погрешности:
Методы решения нелинейных алгебраических уравнений
Метод половинного деления (частный случай метода дихотомии)
![Основная идея метода состоит в следующем: для нахождения корня, принадлежащего отрезку [ , ],](https://present5.com/presentation/15751739_91860122/image-47.jpg "Основная идея метода состоит в следующем: для нахождения корня, принадлежащего отрезку [ , ],")
Основная идея метода состоит в следующем: для нахождения корня, принадлежащего отрезку [ , ], делим отрезок пополам, то есть выбираем начальное приближение Если f( X(0) )=0, то X(0) является корнем уравнения. Если f(X(0) ) 0, то выбирается тот из отрезков [ (0), X(0) ] или [X(0) , (0)], на концах которого функция f(X) имеет противоположные знаки. Новый отрезок будем обозначать [ (1), (1)].
![Неограниченное продолжение итерационного процесса дает последовательность отрезков: [ (1), (1)], [ (2), (2)], .](https://present5.com/presentation/15751739_91860122/image-48.jpg "Неограниченное продолжение итерационного процесса дает последовательность отрезков: [ (1), (1)], [ (2), (2)], .")
Неограниченное продолжение итерационного процесса дает последовательность отрезков: [ (1), (1)], [ (2), (2)], . . . , [ (n), (n)], . . . , содержащих искомый корень. Середина n-го отрезка точка (1) дает приближение к корню оценку погрешности: , имеющее (2) .
![f(x) [α, β] α 2 0 β 2 х α 0 β 0 Геометрическая](https://present5.com/presentation/15751739_91860122/image-49.jpg "f(x) [α, β] α 2 0 β 2 х α 0 β 0 Геометрическая")
f(x) [α, β] α 2 0 β 2 х α 0 β 0 Геометрическая интерпретация итерационного процесса приближения к корню уравнения методом половинного деления.
![f(x) [α 1, β 1] α 2 0 β 2 х α β 1](https://present5.com/presentation/15751739_91860122/image-50.jpg "f(x) [α 1, β 1] α 2 0 β 2 х α β 1")
f(x) [α 1, β 1] α 2 0 β 2 х α β 1 1 Геометрическая интерпретация итерационного процесса приближения к корню уравнения методом половинного деления.
![f(x) [α 2, β 2] α 2 0 β 2 х α β 2](https://present5.com/presentation/15751739_91860122/image-51.jpg "f(x) [α 2, β 2] α 2 0 β 2 х α β 2")
f(x) [α 2, β 2] α 2 0 β 2 х α β 2 2 Геометрическая интерпретация итерационного процесса приближения к корню уравнения методом половинного деления.
Пример. Решить уравнение x 2+2=0 методом половинного деления с точностью ε=0, 5 для поиска корня на интервале (0, 6). α=α 1=0; β= β 1=6. [0; 6] f( α 1)= 02+2=2; f( β 1)= 62+2= 34. f( α 1) f(β 1)=2 ( 34 )<0 Корень есть! X 1=(0+6)/2=3; f(X 1)= 32+2= 7. f( α 1) f(Х 1)=2 ( 7) <0 Корень есть! α 2=α 1=0; β 2=Х 1=3. [0; 3] X 2=(0+3)/2=1, 5; f(X 2)= 1, 52+2= 0, 25. |X 1 X 2|= |3 1, 5|=1, 5>0, 5 Продолжать! f( α 2) f(Х 2)=2 ( 0. 25) <0 Корень есть! α 3=α 2=0; β 3= β 2=Х 2 =1, 5. [0; 1, 5]
![α 3=α 2=0, β 3= β 2=Х 2 =1, 5. [0; 1, 5] X](https://present5.com/presentation/15751739_91860122/image-53.jpg "α 3=α 2=0, β 3= β 2=Х 2 =1, 5. [0; 1, 5] X")
α 3=α 2=0, β 3= β 2=Х 2 =1, 5. [0; 1, 5] X 3=(0+1, 5)/2=0, 75; f(X 3)= 0, 752+2 0, 56. | X 2 X 3 |= |1, 5 0, 56 |=0, 94>0, 5 Продолжать! f( α 3)= 02+2=2; f(X 3 )= 0, 56. f( α 3) f(X 3 )=2 0, 56 >0 Корня нет! f(β 3)= 1, 52+2= 0, 25. f(β 3) f(X 3 )= 0, 25 0, 56 <0 Корень есть! α 4= X 3 = 0, 75; β 4= β 3=1, 5. [0, 75; 1, 5] X 4=(0, 75+1, 5)/2=1, 125 1, 13; f(X 4)= 1, 132+2 0, 72. | X 3 X 4 |= |0, 75 1, 13|=0, 38 < 0, 5 КОНЕЦ!!! КОРЕНЬ= X 4 =1, 13.
Метод хорд В методе половинного деления получение очередного приближения к корню осуществляется по жёстко заданному плану и не учитывает вычисляемые на каждом шаге значения функции. Можно достичь лучших результатов, если отрезок [ , ] делить точкой с на части не пополам, а пропорционально величинам ординат f( ) и f( ) графика заданной функции f(х). Т. е. точку с следует находить как абсциссу точки пересечения оси Ох с прямой, проходящей через точки А( , f( )) и В( , f( )), иными словами, с хордой АВ дуги АВ.
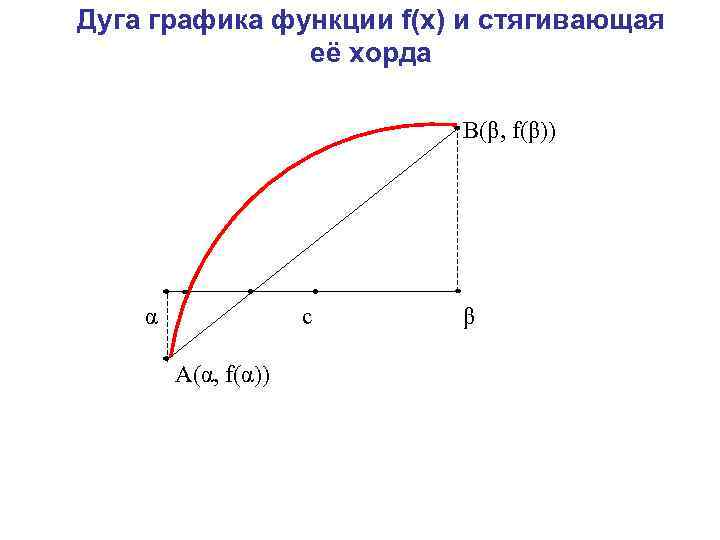
Дуга графика функции f(x) и стягивающая её хорда B(β, f(β)) α с β А(α, f(α))
Уравнение прямой, проходящей через две заданные точки А и В имеет вид: Полагая y=0 и х=с (обозначение искомой точки пересечения прямой АВ с осью Ох), находим Метод, получающийся из метода дихотомии таким фиксированием точки деления очередного отрезка, называется методом хорд.
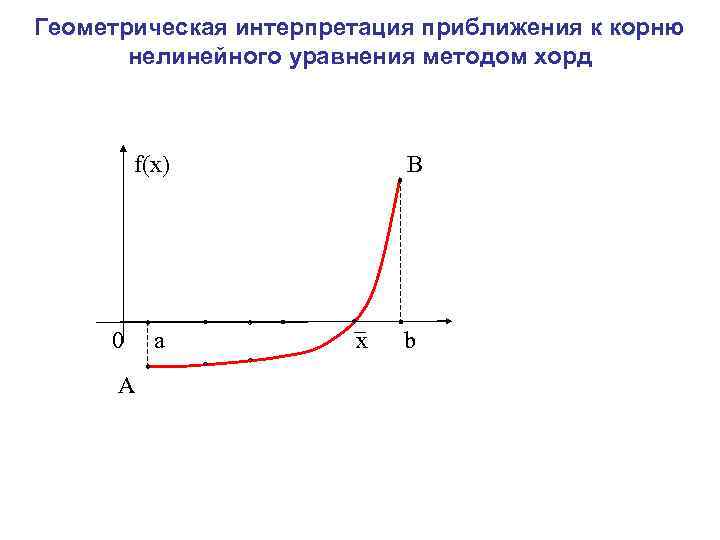
Геометрическая интерпретация приближения к корню нелинейного уравнения методом хорд f(x) В 0 a x 1 x 2 x 3 x b А
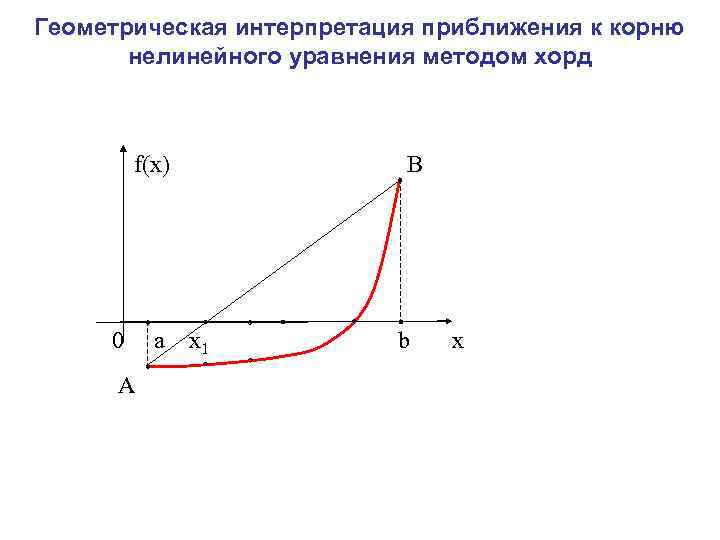
Геометрическая интерпретация приближения к корню нелинейного уравнения методом хорд f(x) В 0 a x 1 x 2 x 3 b x А
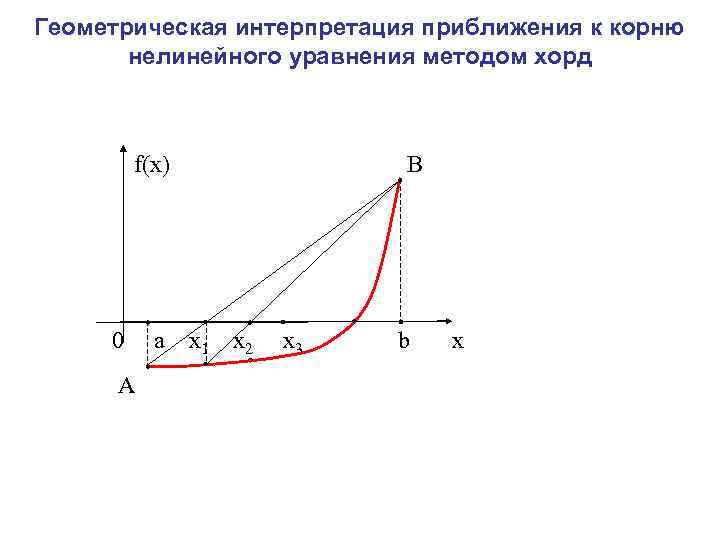
Геометрическая интерпретация приближения к корню нелинейного уравнения методом хорд f(x) В 0 a x 1 x 2 x 3 b x А
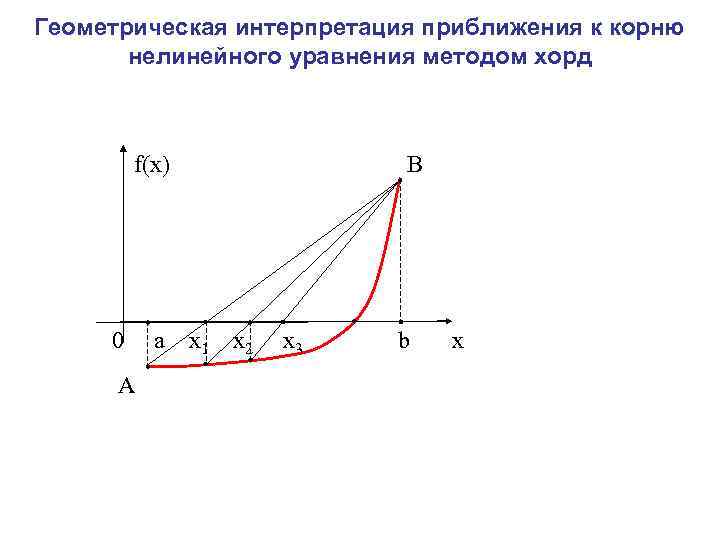
Геометрическая интерпретация приближения к корню нелинейного уравнения методом хорд f(x) В 0 a x 1 x 2 x 3 b x А
Метод последовательных приближений (метод простой итерации) Предположим, что уравнение вида: F(X)=0 (1) преобразовано к виду: X=f(Х). (2) Пусть X(0) является исходным приближенным значением корня. Тогда в качестве первого приближения примем X(1) = f(X(0)), в качестве второго X(2) = f(X(1)) и т. д. Основная расчетная формула в таком случае имеет вид: X(n) = f(X(n-1)). (3)
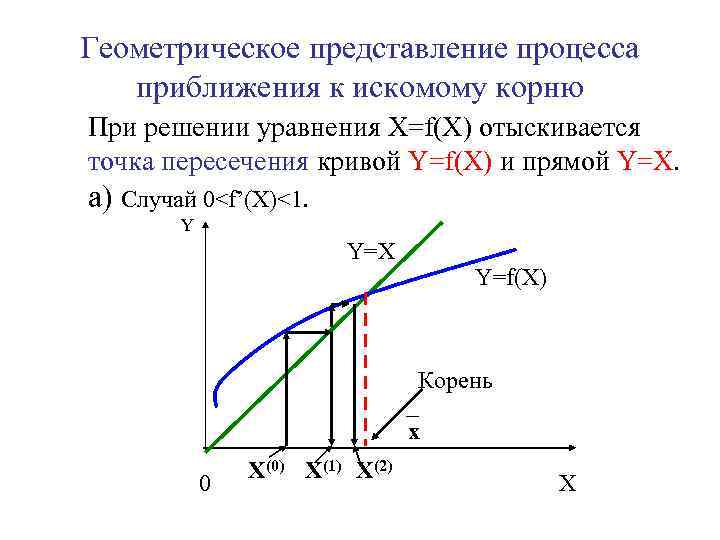
Геометрическое представление процесса приближения к искомому корню При решении уравнения X=f(X) отыскивается точка пересечения кривой Y=f(X) и прямой Y=X. а) Случай 0<f’(X)<1. Y Y=X Y=f(X) Корень х (1) Х Х(0) Х(1) (2) 0 Х(0) Х Х X
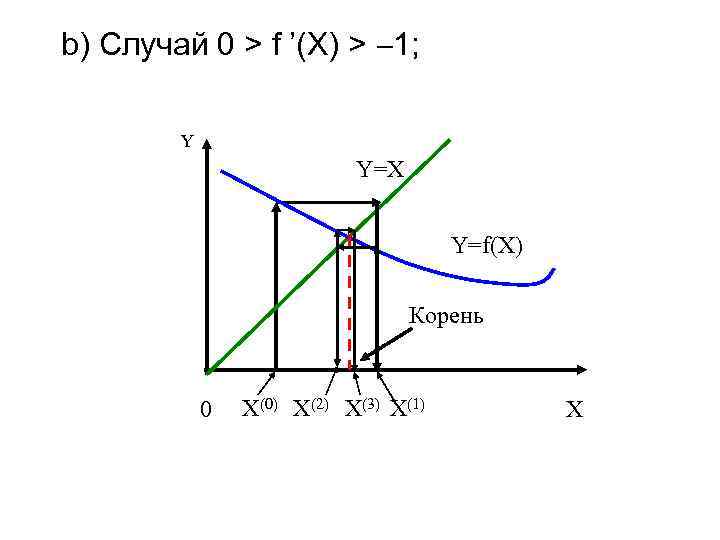
b) Случай 0 > f ’(X) > 1; Y Y=X Y=f(X) Корень Х(0) Х(2) Х(3) Х(1) 0 X
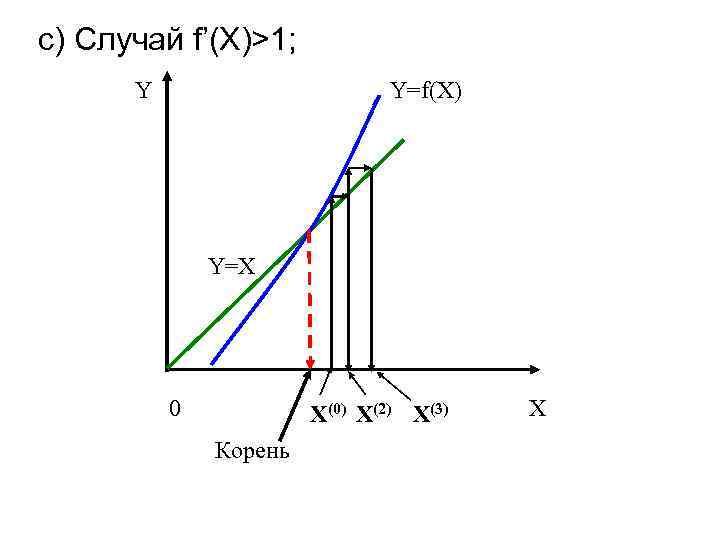
c) Случай f’(X)>1; Y Y=f(X) Y=X 0 X X(0) X(2) X(3) Корень
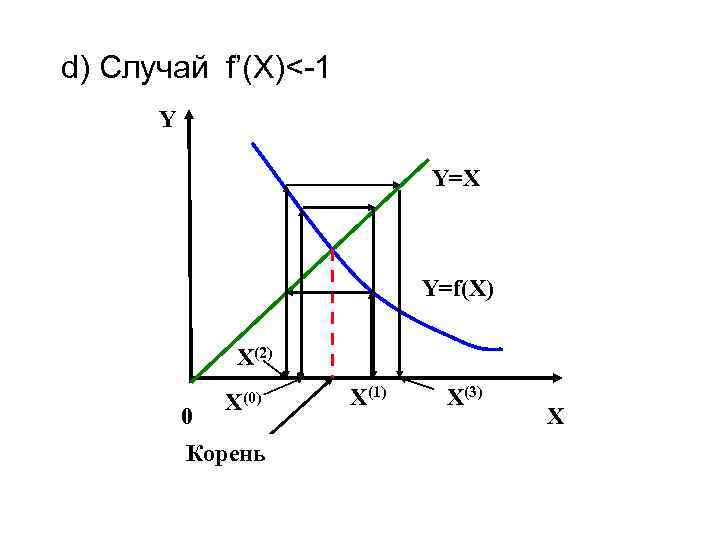
d) Cлучай f’(X)<-1 Y Y=X Y=f(X) X(2) 0 X(0) Корень X(1) X(3) X
Метод Ньютона – Рафсона Описание классического метода Ньютона - Рафсона Предположим, что уравнение f(X)=0 имеет один корень на интервале [ , ], f’(X) и f’’(X) определены, непрерывны и сохраняют постоянные знаки на отрезке [ , ].
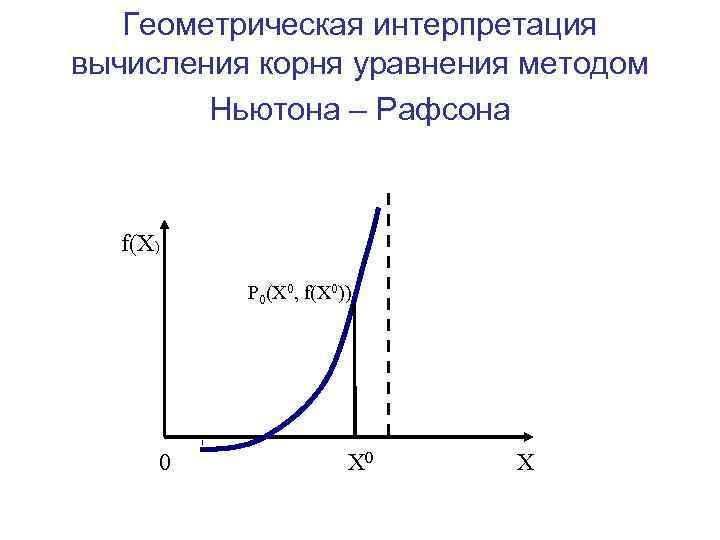
Геометрическая интерпретация вычисления корня уравнения методом Ньютона – Рафсона f(X) P 0(X 0, f(X 0)) P 1(X 1, f(X 1)) 0 X 2 X 1 X 0 X
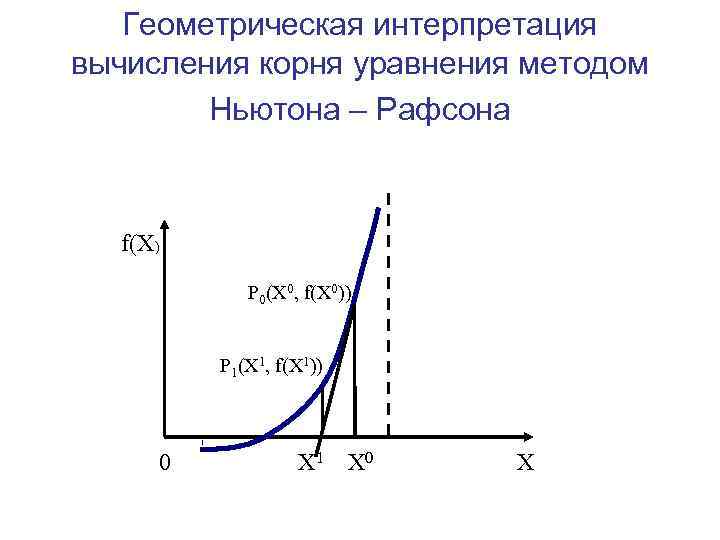
Геометрическая интерпретация вычисления корня уравнения методом Ньютона – Рафсона f(X) P 0(X 0, f(X 0)) P 1(X 1, f(X 1)) 0 X 2 X 1 X 0 X
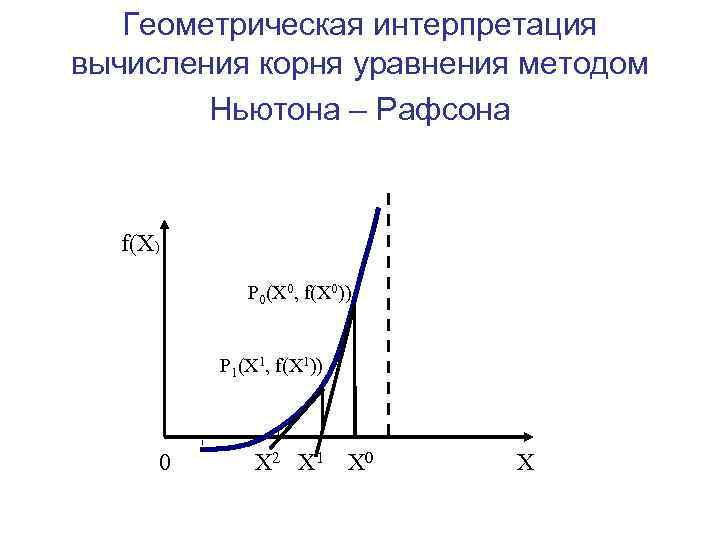
Геометрическая интерпретация вычисления корня уравнения методом Ньютона – Рафсона f(X) P 0(X 0, f(X 0)) P 1(X 1, f(X 1)) 0 X 2 X 1 X 0 X
Уравнение касательной, проходящей через точку P 0, имеет вид: Y = f (X 0) + f’(X 0)(X – X 0). Полагая Y=0, найдем абсциссу X 1 точки пересечения касательной и OX Следующие приближения найдем по формулам: …
Процесс вычисления приближений необходимо прекратить при выполнении условия: где m 1 – наименьшее значение |f’(X)| на отрезке [ , ], M 2 – наибольшее значение |f’’(X)| на том же отрезке. При этом будет выполняться равенство: где ε – предельная абсолютная погрешность корня.
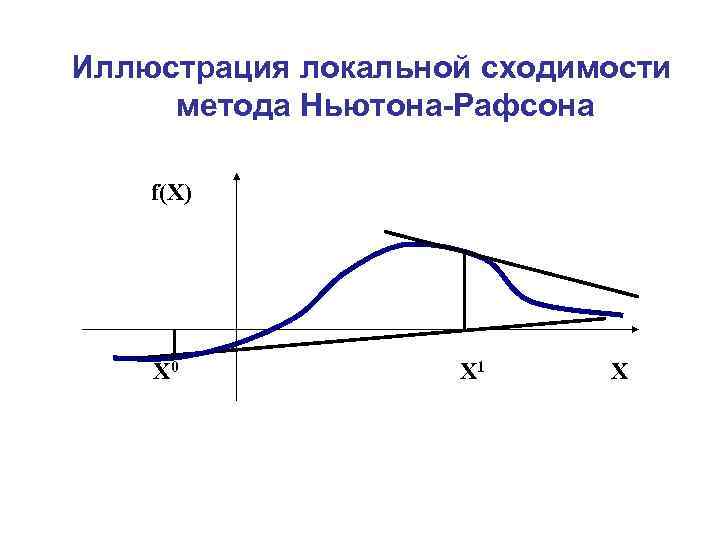
Иллюстрация локальной сходимости метода Ньютона-Рафсона f(X) X 0 X 1 X
Модификации метода Ньютона Упрощенный метод Ньютона Если производная f’(X) непрерывна, то ее значение вблизи простого корня почти постоянно. Поэтому можно попытаться вычислить f’(X) лишь однажды в точке X(0), а затем заменить f’(X(n-1)) постоянной f’(X(0)). В результате получим упрощенную формулу метода Ньютона: n 0
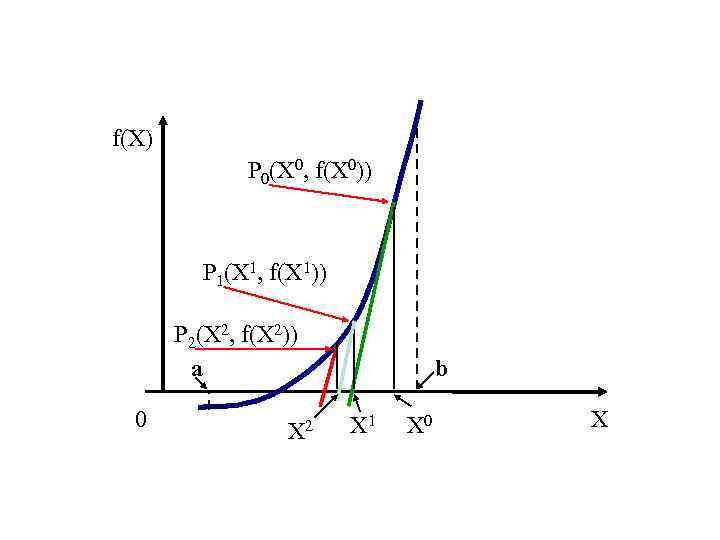
f(X) P 0(X 0, f(X 0)) P 1(X 1, f(X 1)) P 2(X 2, f(X 2)) а b 0 X X 1 X 0 X 2
Метод ложного положения В основе этой и следующей модификаций метода Ньютона лежит приближенное равенство: (1) Оно верно при условии известности Zn и Xn и следует из определения производной: (2)
Пусть C фиксированная точка, расположенная в окрестности простого корня. Заменим в расчетной формуле производную правой частью формулы (1), полагая, что Zn=C. В результате приходим к формуле ложного положения: (3)
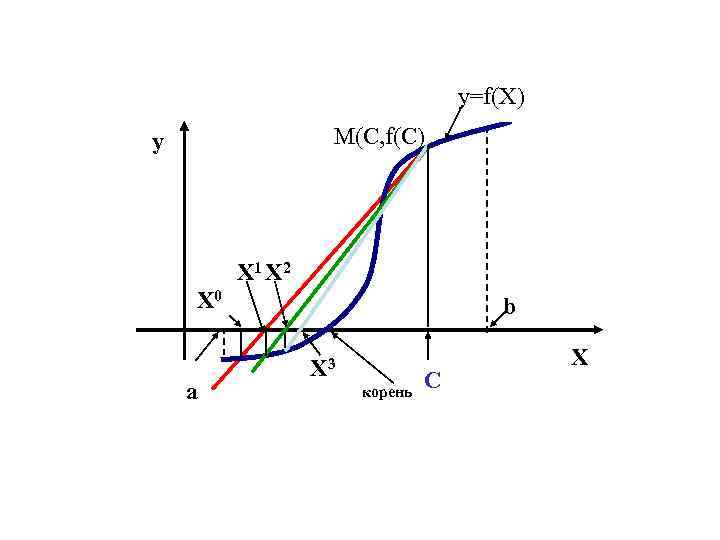
y=f(X) M(C, f(C) y X 1 X 2 X 0 a b X 3 корень С X
Метод секущих Замена в формуле метода Ньютона производной f’(X) приближением: приводит к расчетной формуле для метода секущих: Метод двухшаговый, то есть необходимо задать два начальных приближения: X 0 и X 1
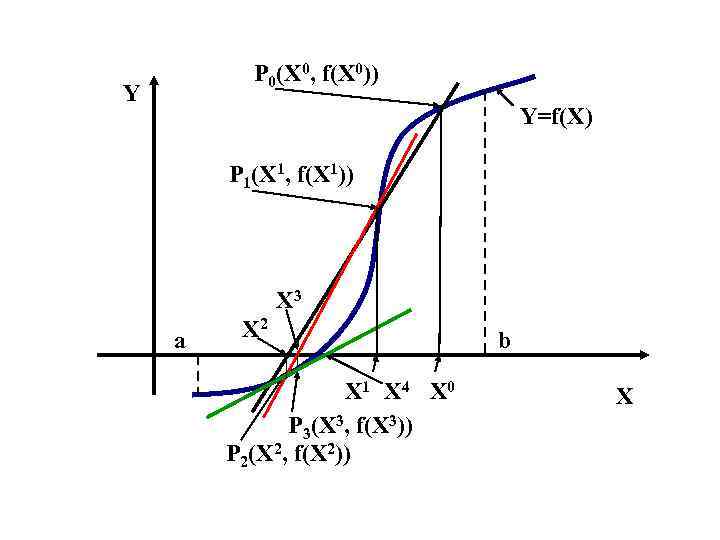
P 0(X 0, f(X 0)) Y Y=f(X) P 1(X 1, f(X 1)) Х 3 a X 2 X 1 Х 4 X 0 3 3 P 3(X , f(X )) 2 2 P 2(X , f(X )) b X
Уточнение метода Ньютона для случая кратного корня Корень X уравнения f(X) = 0 называется простым, если f’( X) 0. В противном случае, то есть если f’( X)=0 – кратным. Целое число m называется кратностью корня X, если f (k)( X) = 0 для k = 1, 2, . . . , m – 1 и f(m)( X) 0.
Для вычисления корня уравнения f (X) = 0 кратности m >1 можно использовать и стандартный метод Ньютона. Однако в этом случае скорость его сходимости является только линейной q = 1 – 1/m. Чтобы сохранить квадратичную скорость сходимости, метод Ньютона нужно модифицировать следующим образом:
Решение ОДУ
Основная идея метода Эйлера Решается дифференциальное уравнение с начальным условием y(x 0)=y 0. В процессе решения составляется таблица значений yk =y(xk). где [a, b] отрезок, на котором ищется решение.
Геометрическая интерпретация метода Эйлера Т. к. в точке x 0 известно значение решения y(x 0)=y 0 и значение его производной y (x 0)=F(x 0, y 0), можно записать уравнение касательной к графику искомой функции y=y(x) в точке (x 0, y 0): y=y 0+ F(x 0, y 0) (x х0). (8. 8)
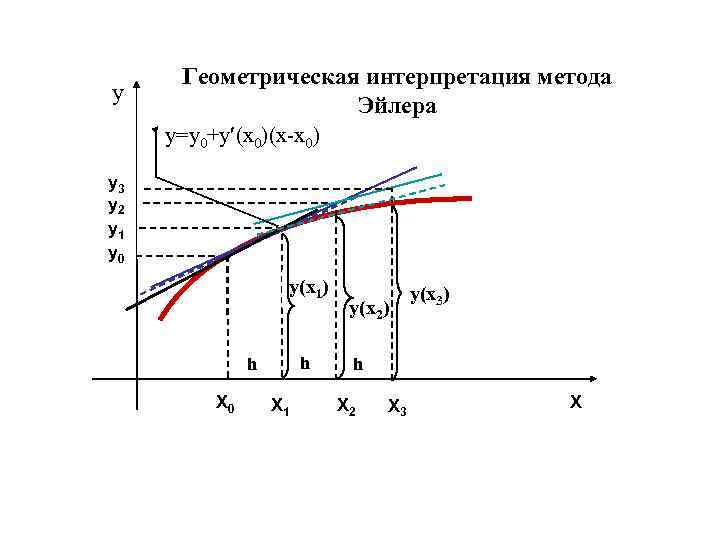
y Геометрическая интерпретация метода Эйлера y=y 0+y (x 0)(x-x 0) y 3 y 2 y 1 y 0 y(x 1) y(x 2) y(x 1) h h Х 0 Х 1 y(x 3) h Х 2 Х 3 Х
Суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой, являющейся касательной к графику функции y=y(x) в точке (xi, y(хi)), т. е. yi+1=yi+ F(xi, yi)h, i=0, 1, …, n. График решения y=y(x) задачи Коши представляется ломаной, составленной из отрезков приближённых касательных.
Пример, иллюстрирующий применение метода Эйлера для решения следующей задачи Коши: y’= x y; (x 0=y 0=0) на сетке с шагом h=0, 1 на интервале [0, 1]. Решение. Данное уравнение уже записано в стандартном виде, разрешенном относительно производной искомой функции, т. е. y =F(x, y). Поэтому, для решаемого уравнения имеем F(x, y)=x y.
Примем шаг интегрирования равным шагу сетки h=0, 1. При этом для каждого узла сетки будет вычислено только одно значение (N=1). Для первых четырех узлов сетки получим следующие результаты: y 1=y(0, 1) y 0+h. F(x 0, y 0)=0+0, 1(0 0)=0; y 2=y(0, 2) y 1+h. F(x 1, y 1)=0+0, 1(0, 1 0)=0, 01; y 3=y(0, 3) y 2+h. F(x 2, y 2)=0, 01+0, 1(0, 2 0. 01)= =0, 029; y 4=y(0, 4) y 3+h. F(x 3, y 3)=0, 029+0, 1(0, 3 0, 029)= =0, 0561 и т. д.
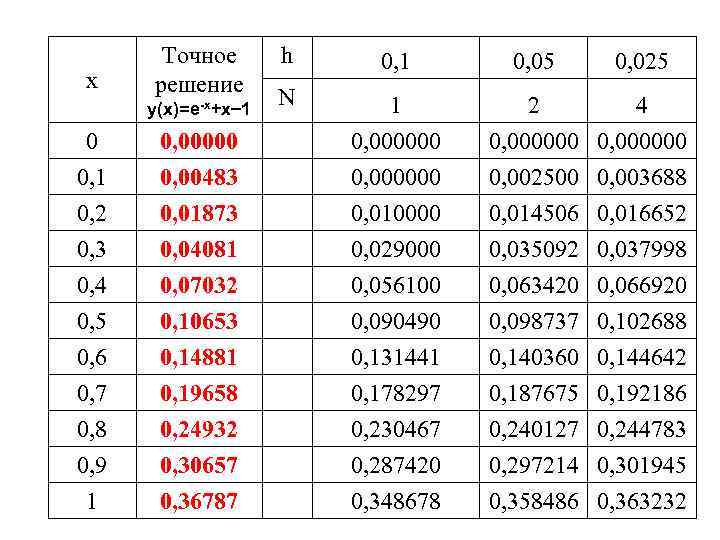
х Точное решение h 0, 1 N 2 4 0, 000000 0, 05 0, 025 0 0, 00000 1 0, 000000 0, 1 0, 00483 0, 000000 0, 002500 0, 003688 0, 2 0, 3 0, 4 0, 01873 0, 04081 0, 07032 0, 010000 0, 029000 0, 056100 0, 014506 0, 016652 0, 035092 0, 037998 0, 063420 0, 066920 0, 5 0, 6 0, 7 0, 8 0, 9 1 0, 10653 0, 14881 0, 19658 0, 24932 0, 30657 0, 36787 0, 090490 0, 131441 0, 178297 0, 230467 0, 287420 0, 348678 0, 098737 0, 140360 0, 187675 0, 240127 0, 297214 0, 358486 y(х)=e-x+x 1 0, 102688 0, 144642 0, 192186 0, 244783 0, 301945 0, 363232
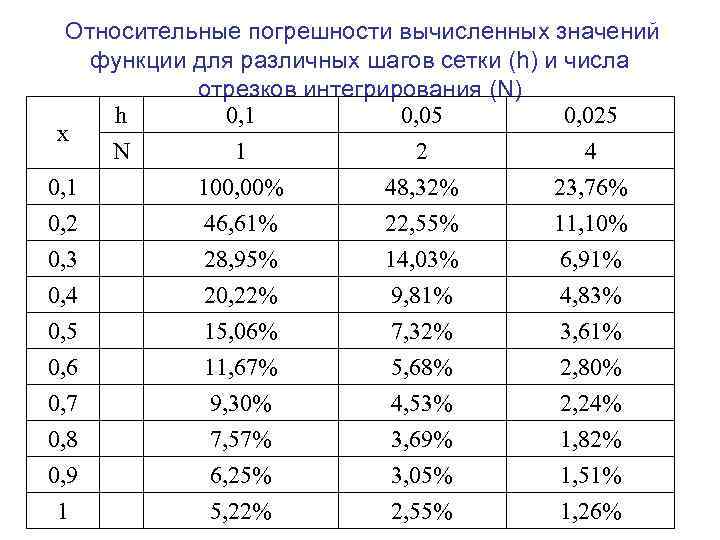
Относительные погрешности вычисленных значений функции для различных шагов сетки (h) и числа отрезков интегрирования (N) h 0, 1 0, 05 0, 025 x N 1 2 4 0, 1 100, 00% 48, 32% 23, 76% 0, 2 46, 61% 22, 55% 11, 10% 0, 3 0, 4 0, 5 0, 6 0, 7 0, 8 0, 9 28, 95% 20, 22% 15, 06% 11, 67% 9, 30% 7, 57% 6, 25% 14, 03% 9, 81% 7, 32% 5, 68% 4, 53% 3, 69% 3, 05% 6, 91% 4, 83% 3, 61% 2, 80% 2, 24% 1, 82% 1, 51% 1 5, 22% 2, 55% 1, 26%
Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений n -го порядка Применение метода Эйлера для решения дифференциального уравнения n-го порядка
Уравнение сводится к системе n обыкновенных дифференциальных уравнений первого порядка заменой производных y’, y’’, …. , y(n-1) на независимые функции P 1(x), P 2(x), Pn-1(x), соответственно.
В результате такой замены получим систему n дифференциальных уравнений 1 -го порядка: причем исходные начальные условия преобразуются в следующую совокупность начальных условий:
Пример решения типовой задачи Пусть необходимо решить, применяя метод Эйлера, дифференциальное уравнение второго порядка: y 2 y +sin(xy)+x=0, для которого заданы начальные условия: x 0=0, y 0=y(x 0)=1, y 0=y (x 0)=1.
Сначала необходимо понизить порядок дифференциального уравнения. Введём в рассмотрение новую функцию Р(x, y)= y (x, y). Тогда исходное уравнение может быть представлено системой из двух дифференциальных уравнений 1 -го порядка: y (x, y)=P(x, y) P (x, y)=2 P(x, y) sin(xy) x. Начальные условия для уравнений этой системы: x 0=0, y 0=1, Р 0=1.
Расчётные формулы для получения решения методом Эйлера имеют вид: yi+1=yi+h Pi , Pi+1=Pi+h (2 Pi sin(xi yi) xi). Начальные условия: x 0=0, y 0=1, Р 0=1.
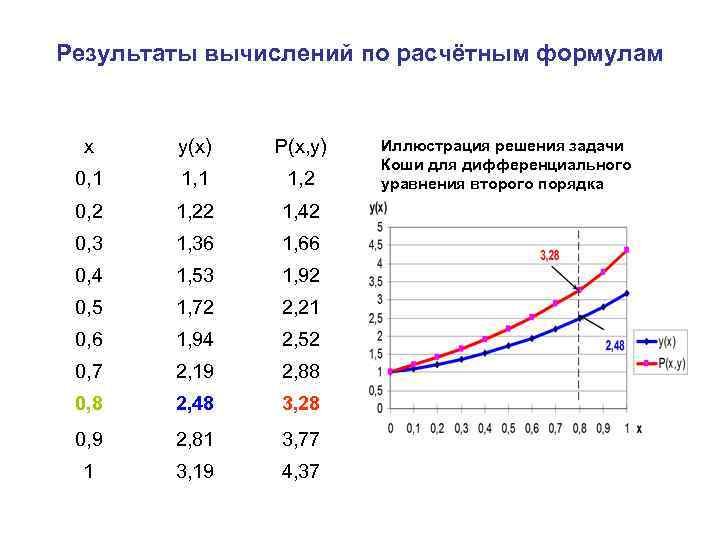
Результаты вычислений по расчётным формулам x y(x) P(x, y) 0, 1 1, 2 0, 2 1, 22 1, 42 0, 3 1, 36 1, 66 0, 4 1, 53 1, 92 0, 5 1, 72 2, 21 0, 6 1, 94 2, 52 0, 7 2, 19 2, 88 0, 8 2, 48 3, 28 0, 9 2, 81 3, 77 1 3, 19 4, 37 Иллюстрация решения задачи Коши для дифференциального уравнения второго порядка
Алгоритм Рунге-Кутты третьего порядка (погрешность порядка h 3) где
Алгоритм Рунге-Кутты четвертого порядка (погрешность порядка h 4) На каждом шаге вычисления выполняются по формуле где
Пример. Используя алгоритм Рунге-Кутты третьего и четвертого порядков решить ДУ y’=x-y x 0=0, y 0=0 с шагом h=0. 1: Решение. Для алгоритма третьего порядка (для узла x=0. 1) вычисления таковы: k 1=hf(x 0, y 0)=0. 1(0 -0)=0 k 2=hf(x 0+h/2, y 0+k 1/2)=0. 1[(0+0. 05)-(0+0/2]=0. 005 k 3=hf(x 0+h/2, y 0+2 k 1 -k 0)=0. 1[(0+0. 1)-(0+2 0. 005 -0]=0. 009 y 1=y 0+1/6(k 1+4 k 2+k 3)=1/6(0+4 0. 005+0. 009)=0. 0048333
Для алгоритма четвертого порядка (для узла x=0. 1) вычисления таковы: k 1=hf(x 0, y 0)=0. 1(0 -0)=0 k 2=hf(x 0+h/2, y 0+k 1/2)=0. 1[(0+0. 05)-(0+0/2]=0. 005 k 3=hf(x 0+h/2, y 0+k 2/2)=0. 1[(0+0. 05)-(0+ 0. 005/2)]= =0. 00475 k 4=hf(x 0+h, y 0+k 3)=0. 1[(0+0. 1)-(0+0. 00475)]= =0. 009525 y 1=y 0+1/6(k 1+2 k 2+2 k 3+k 4)= =1/6(0+2 0. 005+2 0. 00475+0. 009525)=0. 0048375
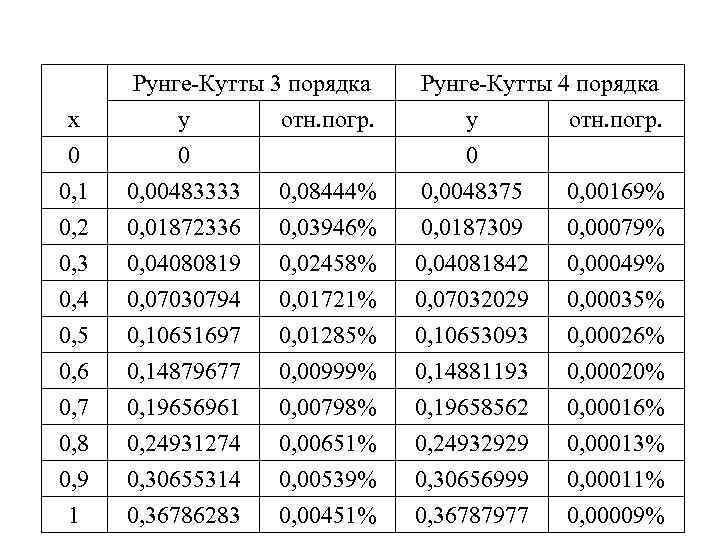
x 0 0, 1 Рунге-Кутты 3 порядка y отн. погр. 0 0, 00483333 0, 08444% Рунге-Кутты 4 порядка y отн. погр. 0 0, 0048375 0, 00169% 0, 2 0, 3 0, 4 0, 5 0, 6 0, 7 0, 8 0, 9 1 0, 01872336 0, 04080819 0, 07030794 0, 10651697 0, 14879677 0, 19656961 0, 24931274 0, 30655314 0, 36786283 0, 0187309 0, 04081842 0, 07032029 0, 10653093 0, 14881193 0, 19658562 0, 24932929 0, 30656999 0, 36787977 0, 03946% 0, 02458% 0, 01721% 0, 01285% 0, 00999% 0, 00798% 0, 00651% 0, 00539% 0, 00451% 0, 00079% 0, 00049% 0, 00035% 0, 00026% 0, 00020% 0, 00016% 0, 00013% 0, 00011% 0, 00009%
Пример решения типовой задачи Пусть необходимо, применяя метод Рунге. Кутты, решить дифференциальное уравнение второго порядка: y 2 y +sin(xy)+x=0, для которого заданы начальные условия: x 0=0, y 0=y(x 0)=1, y 0=y (x 0)=1.
Понизим порядок дифференциального уравнения. Введём в рассмотрение новую функцию Р(x, y)= y (x, y). Тогда исходное уравнение может быть представлено системой из двух дифференциальных уравнений 1 -го порядка: y (x, y)=P(x, y) P (x, y)=2 P(x, y) sin(xy) x. Начальные условия для уравнений этой системы: x 0=0, y 0=1, Р 0=1.
Расчётные формулы для получения решения методом Рунге-Кутты имеют вид:
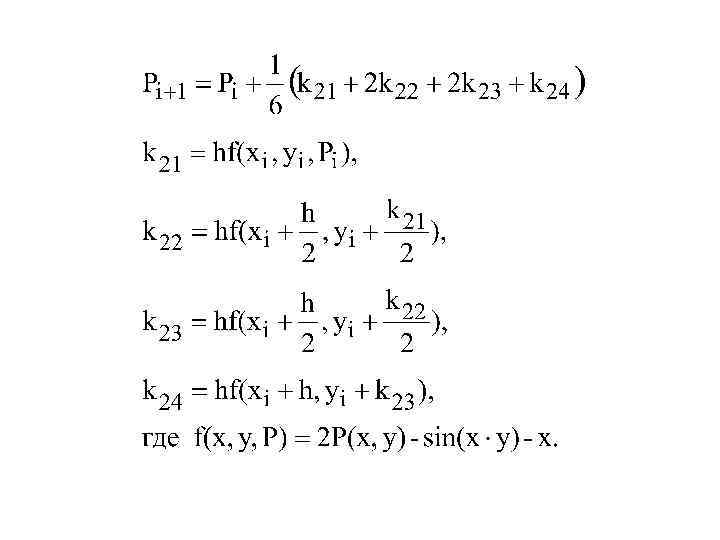
Для нашего примера расчётные формулы имеют вид: т. е. Формула Эйлера
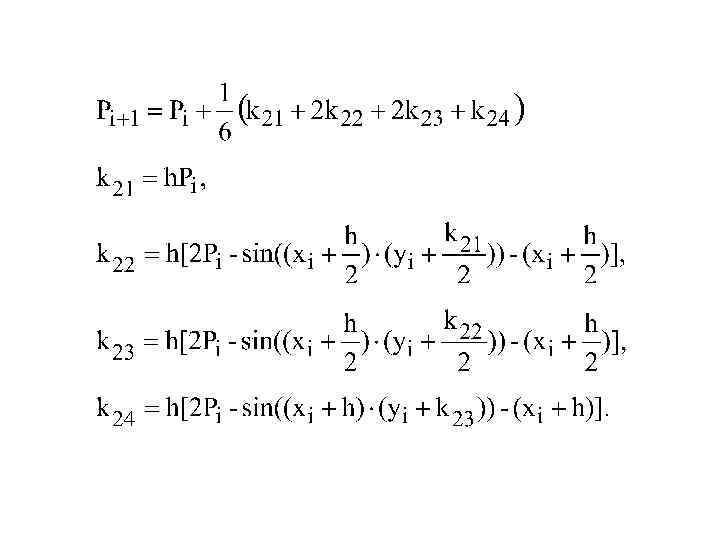
Правило двойного пересчёта (правило Рунге) Пусть значение в точке Xi найдено и равно Yi. 1) Обозначим через Yhi+1 приближение Yi+1 к Y(Xi+1), найденное с помощью некоторого одношагового метода: Yhi+1 =Yi+1= Yi+hi+1 Ф(Xi, Yi, hi+1), (1) который имеет порядок точности р. Уменьшим шаг интегрирования вдвое, положив
2) Вычислим приближение к значению в точке Xi+1 с помощью то же одношагового метода, но с половинным шагом hi+1/2 : Yi+1/2= Yi + hi+1/2 Ф(Xi, Yi, hi+1/2), Yi+1= Yi+1/2 + hi+1/2 Ф(Xi+1/2, Yi+1/2, hi+1/2 ), Полученное таким образом значение Yhi+1/2= Yi+1 будет отличаться от значения, найденного по формуле (1).
3) Для оценки локальной (Li+1) погрешности значения Yhi+1/2 принимается приближенное равенство: Li+1=Yi+1(Xi+1) Yhi+1/2 ≈(Yhi+1/2 Yhi+1)/(2 p 1), называемое правилом двойного пересчёта или правилом Рунге.
Методы решения систем линейных алгебраических уравнений
Метод Гаусса (метод последовательного исключения неизвестных) Решение системы линейных алгебраических уравнений с помощью метода Гаусса состоит из двух основных этапов: 1) Прямого хода; 2) Обратного хода (обратной подстановки).
Прямой ход заключается в последовательном исключении неизвестных из системы a 11 x 1+a 12 x 2+…+a 1 mxm =b 1 a 21 x 1+a 22 x 2+…+a 2 mxm =b 2 …………… (1) am 1 x 1+am 2 x 2+…+ammxm=bm. для преобразования её к эквивалентной системе линейных алгебраических уравнений с верхней треугольной матрицей: Вычисление значений неизвестных производят на этапе обратного хода.
9. 4. 1 Схема единственного деления. Прямой ход решения состоит из (m– 1)го шага исключения неизвестных. 1 -й шаг. Целью этого шага является исключение неизвестного х1 из уравнений с номерами i = 2, 3, …, m. Предположим, что коэффициент a 11 0. Главный (ведущий) элемент 1 -го шага
Множители 1 -го шага Найдём величины i 1 = ai 1 / a 11, ( i = 2, …, m), Вычтем последовательно из 2 -го, 3 -го, …, m-го уравнений системы (1) первое уравнение, умноженное соответственно на 21, 31, …, m 1. Это позволит обратить в нуль коэффициенты при неизвестном х1 во всех уравнениях системы, кроме первого уравнения.
В результате получим эквивалентную систему линейных алгебраических уравнений: a 11 x 1 + a 12 x 2 + … + a 1 mxm = b 1 a(1)22 x 2 +… + a(1)2 mxm = b(1)2 a(1)32 x 2 +… + a(1)3 mxm = b(1)3 (2) …………………………. a(1)m 2 x 2 +… + a(1)mmxm = b(1)m, где a(1)ij = aij - i 1 a 1 j , b(1)i = bi - i 1 b 1. (3)
2 -й шаг. Целью этого шага является исключение неизвестного х2 из уравнений с номерами i = 3, 4, …, m. Множители второго шага исключения: i 2 = a(1)i 2 / a(1)22 , (i = 3, 4, …, m). Вычтем последовательно из третьего, четвертого, …, m-го уравнений системы (2) второе уравнение, умноженное соответственно на 32, 42, …, m 2.
В результате получим систему: a 11 x 1 + a 12 x 2 + … + a 1 m xm = b 1 a(1)22 x 2 +… +a(1)2 mxm = b(1)2 a(2)33 x 3 +… + a(2)3 mxm = b(2)3 ……………………… (4) a(2)m 3 x 3 +… + a(2)mmxm= b(2)m, где a(2)ij = a(1)ij - i 2 a(1)2 j , b(2)i = b(1)i - i 2 b(1)2. (5)
k-й шаг. В предположении, что главный элемент k - го шага a(k-1)kk≠ 0, вычислим множители: ik = a(k-1)ik / a(k-1)kk , (i = k+1, …, m) и вычтем из (k+1)-го, (k+2)-го, …, m -го уравнений полученной на предыдущем шаге системы k-ое уравнение, умноженное соответственно на k+1, k; k+2, k; … ; mk.
После (m-1)-го шага получим: a 11 x 1 + a 12 x 2 + … + a 1 m xm = b 1 a(1)22 x 2 +… + a(1)2 mxm = b(1)2 a(2)33 x 3 +… + a(2)3 mxm = b(2)3 …………… (6) a(m-1)mmxm= b(m-1)m, Матрица А(m-1) является треугольной.
Обратный ход Из последнего уравнения системы (6) находим значение неизвестного xm. Подставляя найденное значение в предпоследнее уравнение, получаем значение xm-1. Осуществляя обратную подстановку, далее последовательно находим xm-2, xm-1, …, x 1. Вычисление неизвестных здесь проводится по формулам: b(m-1)m xm = --------- ; a(m-1)mm (7) b(k-1)k – a(k-1)k, k+1 xk+1 – … – a(k-1)kmxm xk = ----------------------- ; a (k-1)kk k = m-1, …, 1.
Итерационные методы решения систем линейных алгебраических уравнений Метод простой итерации
Приведение системы уравнений к виду, удобному для итераций АХ = Р (1) А - квадратная невырожденная матрица Необходимо предварительно преобразовать эту систему к виду: Х = ВХ + С. (2) Здесь В – квадратная матрица с элементами bij (i, j [1, m]), С – вектор-столбец с элементами сi (i [1, m]).
Самый простой способ приведения системы к виду (2) состоит в следующем: Из первого уравнения системы (1) выразим неизвестное x 1: х1 = (р1 – а 12 х2 – а 13 х3–…–а 1 mхm) / а 11 ; Из второго уравнения – неизвестное х2 : х2 = (р2 – а 22 х2 – а 23 х3–…– а 2 mхm) / а 22 , и т. д.
В результате получим систему в виде (3): х1 = b 12 x 2 +b 13 x 3+…+b 1, m-1 xm-1+ b 1 mxm +c 1 х2 = b 21 x 1 +b 23 x 3+… + b 2, m-1 xm-1+ b 2 mxm + c 2 …………… хm = bm 1 x 1+bm 2 x 2 +… +bm, m-1 xm-1 +cm.
В главной диагонали матрицы В находятся нулевые элементы. Остальные элементы вычисляются по формулам: (4)
Описание метода Выбираем некоторое начальное приближение вектора решения: Х(0) = (х1(0), х2(0), …, хm(0))Т. Подставляя его в правую часть системы (2) и вычисляя полученное выражение, находим первое приближение: Х(1)= ВХ(0) + С. Подставляя приближение Х(1) в правую часть системы (2), получим: Х(2) = ВХ(1) + С, и. т. д.
Таким образом, основная расчетная формула имеет вид: Х(k+1) = ВХ(k) + С. (5) В случае, когда используется система (3) с коэффициентами, вычисляемыми по формуле (4), метод простой итерации называется методом Якоби.
Метод Зейделя для решения систем линейных алгебраических уравнений Описание метода Пусть система (1) приведена к виду (3) с коэффициентами, вычисленными по формуле (4). Метод Зейделя можно рассматривать как модификацию метода Якоби. Основная идея метода состоит в том, что при вычислении очередного( k+1) – го приближения к неизвестному xi при i > 1 используют уже найденные ( k+1)–е приближения к неизвестным х1, х2, …, хi-1, а не k –е, как в методе Якоби
Основная идея метода Зейделя состоит в том, что при вычислении очередного( k+1) – го приближения к неизвестному xi при i > 1 используют уже найденные ( k+1)–е приближения к неизвестным х1, х2, …, хi-1, а не k –е, как в методе Якоби
х1(k+1) = b 12 x 2 (k) + b 13 x 3 (k) +… +b 1 mxm (k) х2 (k+1) = b 21 x 1 (k+1) + c 1 + b 13 x 3 (k) +… +b 1 mxm (k) + c 2 х3 (k+1)= b 31 x 1 (k+1)+ b 32 x 2 (k+1) +… +b 1 mxm (k) + c 3 …………………………… хm (k+1) = bm 1 x 1 (k+1) + … …………. +bm, m-1 xm-1 (k+1) + cm
Введём верхнюю и нижнюю треугольные матрицы: В 1 = и В 2 = .
Тогда расчетная формула примет компактный вид: Х(k+1) = В 1 Х(k+1) + В 2 Х(k) + С. Заметим, что матрица В = В 1 + В 2 и поэтому решение X системы удовлетворяет равенству: X= В 1 + В 2 X+ С. Метод Зейделя иногда называют методом Гаусса – Зейделя или процессом Либмана, или методом последовательных замещений.
Геометрическая интерпретация метода Зейделя a 11 x 1 + a 12 x 2 = b 1 - прямая L 1; a 21 x 1 + a 22 x 2 = b 2 - прямая L 2. Расчётные формулы для решения этой системы имеют вид: х1(k+1) = b 12 x 2(k) + c 1 х2(k+1) = b 21 x 2 k+1) + c 2,
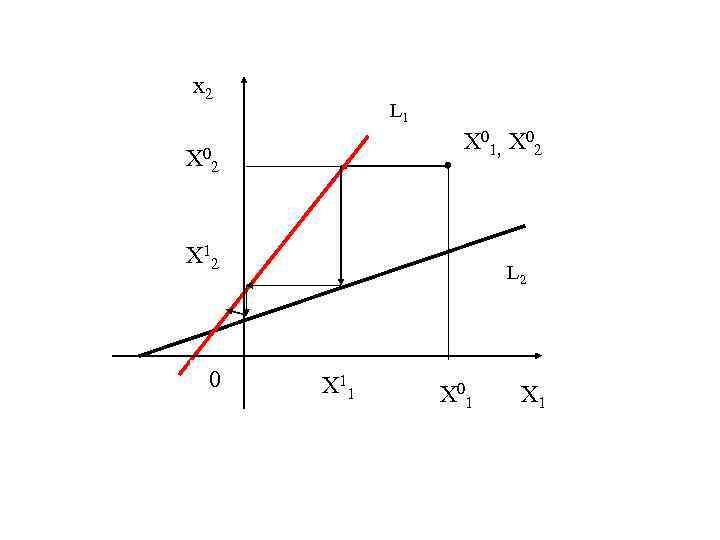
x 2 L 1 X 01, Х 02 X 12 0 L 2 Х 11 Х 01 Х 1
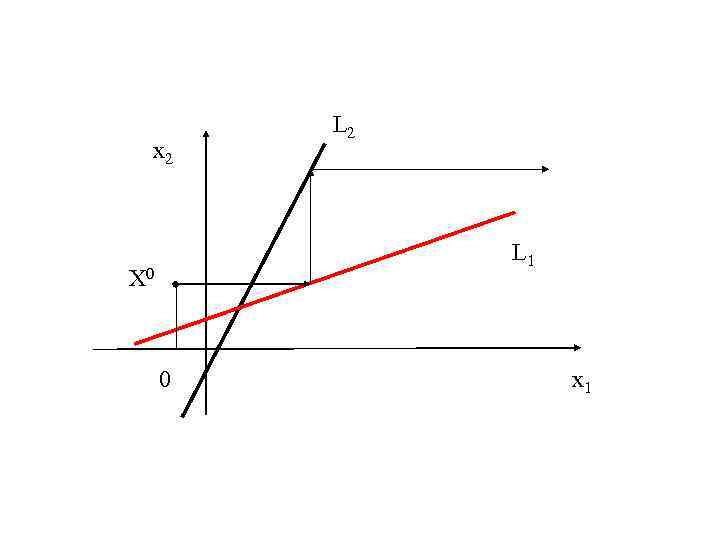
x 2 X 0 0 L 2 L 1 x 1
Скачать презентацию Приближение функций Пример Получить приближение функции f x
Примеры для подготовки к экзамену АиМВ.ppt