Данильченко.Лекции.часть 3.pptx
- Количество слайдов: 67

При построении таблицы разностей мы до сих пор предполагали, что значения аргумента функции являются равноотстоящими т. е. имеют постоянный шаг. Однако на практике встречаются таблицы для не равноотстоящих значений аргумента, т. е. таблицы с переменным шагом. Для таких таблиц понятие конечных разностей обобщается в так называемые разделенные разности. Пусть функция у = f(x) задана таблицей и х0, х1, х2, … – значения аргументов, а у0, у1, у2, … - соответствующие значения функции, где разности Δх1 = хi+1 – xi ≠ 0, (i = 0, 1, 2, …) не равны между собой.

Отношения называются разделенными разностями первого порядка. Например, Аналогично определяются разности второго порядка Например

Вообще разделенные разности n-го порядка получаются из разделенных разностей (n-1) – го порядка с помощью рекуррентного соотношения Заметим, что разделенные разности не меняются при перестановке элементов, т. е. представляют собой симметрические функции своих аргументов. Например
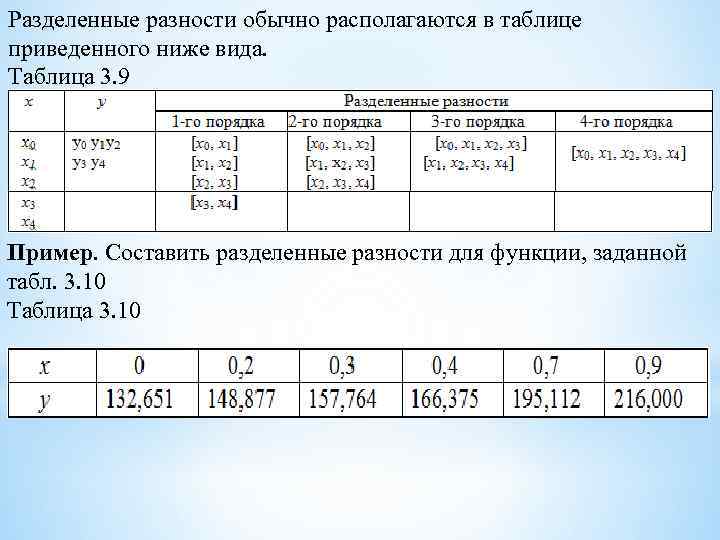
Разделенные разности обычно располагаются в таблице приведенного ниже вида. Таблица 3. 9 Пример. Составить разделенные разности для функции, заданной табл. 3. 10 Таблица 3. 10

Решение. Последовательно применяя формулу (3. 19), получим.
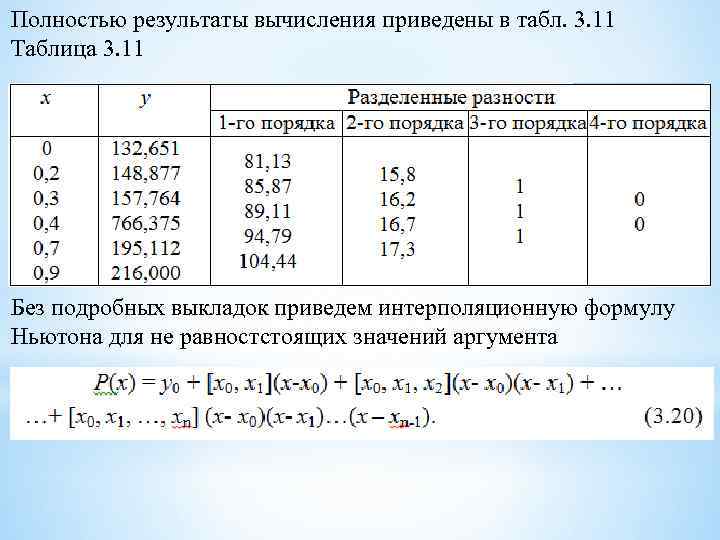
Полностью результаты вычисления приведены в табл. 3. 11 Таблица 3. 11 Без подробных выкладок приведем интерполяционную формулу Ньютона для не равностстоящих значений аргумента

Погрешность этой формулы определяется, как обычно, выражением (3. 17): где ξ – промежуточное значение между точками х0, х1, х2, . . . , хn и х. Пример. Составить интерполяционный полином для функции y = f(x), заданной табл. 3. 12. Таблица 3. 12 С помощью этого полинома найти f(3, 7608)
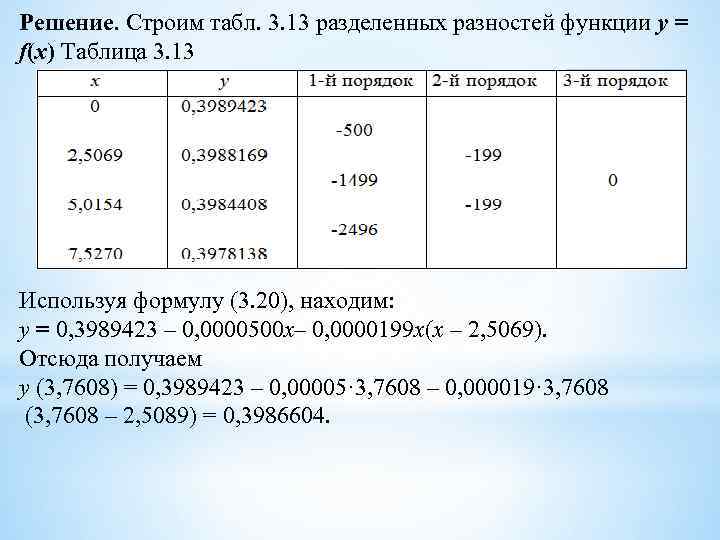
Решение. Строим табл. 3. 13 разделенных разностей функции y = f(x) Таблица 3. 13 Используя формулу (3. 20), находим: y = 0, 3989423 – 0, 0000500 х– 0, 0000199 х(х – 2, 5069). Отсюда получаем y (3, 7608) = 0, 3989423 – 0, 00005· 3, 7608 – 0, 000019· 3, 7608 (3, 7608 – 2, 5089) = 0, 3986604.

4. Эмпирические формулы. Из выше изложенного материала ясно, что любую функцию можно с достаточной степенью точности заменить интерполяционным многочленом. Однако, чтобы добиться достаточно хорошего совпадения, может потребоваться использование многочлена сравнительно высокой степени. Такой многочлен будет неудобен в обращении ввиду его громоздкости, коэффициенты такого многочлена могут и не иметь физического смысла. Поэтому при проведении натурных экспериментальных исследований или вычислительных экспериментов часто используют другие подходы при установлении неизвестной функциональной зависимости между значениями переменных x и y. Такие зависимости принято называть эмпирическими формулами. Они, как правило, имеют более простой вид, позволяют производить интерполирование и применять к экспериментальным данным методы математического анализа.

Итак, пусть в результате ряда измерений величин x и y получена таблица их значений. Если аналитическое выражение функции f(x) неизвестно или весьма сложно, то возникает практически важная задача: найти эмпирическую формулу значения которой при возможно мало отличалось бы от опытных данных (i=1, 2, …, n).

В такой постановке наша задача весьма неопределенна. Поэтому обычно указывают достаточно узкий класс функций K (например, линейных, степенных, показательных и т. п. ), которому должна принадлежать искомая функция f(x). Дело, таким образом, сведется к нахождению лишь наилучших значений параметров этой функции. Геометрически задача построения эмпирической формулы состоит в проведении кривой Г вида (1) из некоторого класса К, «возможно ближе» примыкающей к системе точек (i = 1, 2, …, n), как показано на рисунке 1.
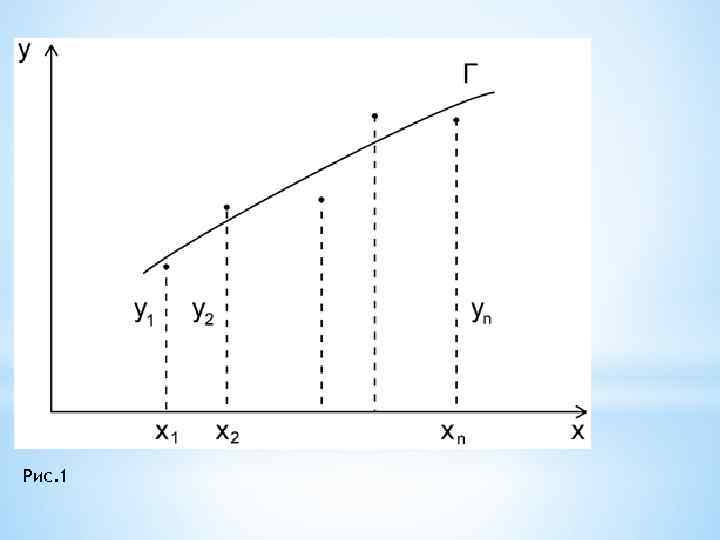
Рис. 1

Заметим, что задача построения эмпирической формулы отлична от задачи интерполяции. При интерполировании отыскивается функция из данного класса функций (например, полиномов заданной степени), значения которой в заданных точках совпадали бы с табличными значениями (i = 1, 2, …, n). При нахождении эмпирической формулы не требуется, чтобы значения f(x) совпадали с Y. Достаточно, чтобы разность была мала в известном смысле в данной области. Построение эмпирической формулы слагается из двух этапов. Выяснение общего вида этой формулы; Определение наилучших ее параметров. Если неизвестен характер зависимости между данными величинами x и y, то предпочтение отдается простым формулам. Нельзя указать общего метода для нахождения наилучшего типа формулы, соответствующей опытным данным.

Удачный выбор эмпирической формулы в значительной мере зависит от опыта и искусства экспериментатора (составителя формулы, – составитель и экспериментатор не всегда могут быть одним и тем же лицом). В некоторых случаях выбор типа эмпирической формулы может быть произведен на основе теоретических представлений о характере изучаемой зависимости. В других случаях удается подобрать такую формулу, сравнивая кривую, построенную по данным наблюдения, с образцами известных кривых, построенных в декартовых системах координат или в специальных системах координат (полулогарифмической, логарифмической и т. д. ). При определенном навыке по положению точек, определяющих некоторую гладкую кривую, можно примерно угадать общий вид зависимости. Что касается определения наилучших значений параметров, входящих в эмпирическую формулу, то эта задача более легкая и решается регулярными методами.

При построении эмпирической формулы можно предположить, что исходные данные положительны. Действительно, если бы, например, все (или все ), то достаточно рассмотреть таблицу значений или. При и достаточно построить эмпирическую формулу для таблицы. В общем случае, когда знаки значений x и y меняется, то всегда можно подобрать положительные числа m и n такие, что Отсюда получаем, что решение поставленной задачи сводится к нахождению эмпирической формулы для системы положительных значений. .

4. 1. Линейная зависимость Пусть расположение опытных точек таково, что они лежат вблизи прямой L (см. рис. 2). В этом случае эмпирическую формулу будем искать в виде линейной функции Для нахождения параметров a и b применяют несколько способов. 1) Способ натянутой нити. Строим точечный график на миллиметровой бумаге в достаточно крупном масштабе. Проводим прямую, близкую к опытным данным. Измеряем отрезок, отсекаемый прямой на оси ординат, это будет b. Найдем tg угла между прямой и осью абсцисс, это будет a. Эмпирическая формула готова. (b=0, 147 при x=10; y=1, 138 )
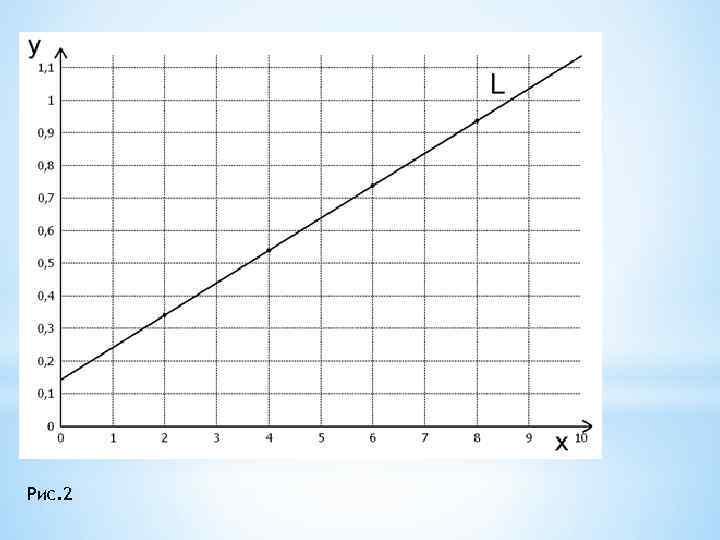
Рис. 2

Способ выбранных точек. Для нахождения параметров a и b измеряют координаты двух точек и , лежащих на прямой L и по возможности удаленных друг от друга. Тогда a и b могут быть определены из системы уравнений 3) Способ средней. Пусть опытные значения записаны в таблице.

Равенство (4. 1) запишем в виде (4. 3) Если вместо x и y представить какие-нибудь опытные значения, то, так как они приближенные, получим не нуль, а некоторое малое число , называемое невязкой. Например, Все ошибки носят случайный характер. Поэтому при довольно большом числе измерений положительные и отрицательные невязки уравниваются, и сумма всех невязок равна нулю.

Отсюда укажем способ отыскания чисел a и b в уравнении (4. 2). Все опытные точки разделим на две группы, одинаковые или почти одинаковые по числу точек (В общем случае все опытные точки разбиваются на столько групп, сколько неизвестных в эмпирической формуле. Так, для параболы разбиваем на три группы). Для всех уравнений первой группы найдем невязки и суммы их приравняем нулю. То же проделаем для уравнений второй группы. При этом числа a и b остаются неизвестными. Мы получили два линейных уравнения с двумя неизвестными. Решая систему, найдем a и b. Пример. Зависимость y от x дается таблицей. x 0 3 5 8 10 14 17 20 22 24 y 1, 02 2, 50 3, 92 5, 16 6, 82 8, 36 10, 74 11, 82 13, 64 12, 96 По этим данным построим эмпирическую формулу разными способами.
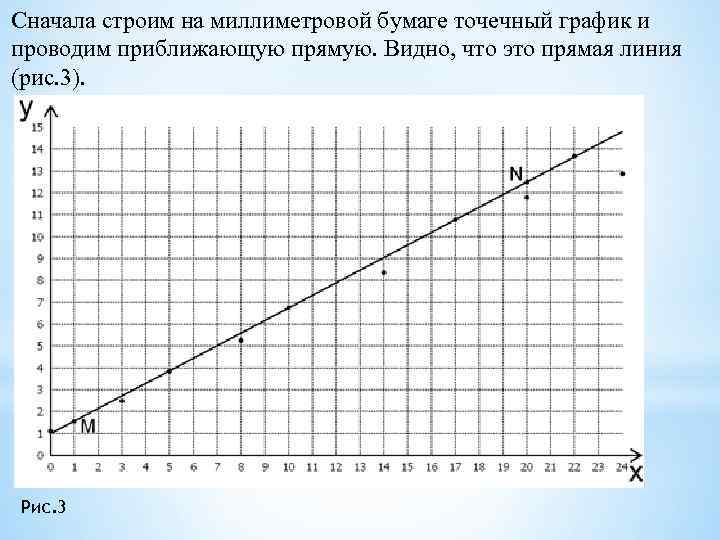
Сначала строим на миллиметровой бумаге точечный график и проводим приближающую прямую. Видно, что это прямая линия (рис. 3). Рис. 3

Решение способом натянутой нити. Из рис. 3 видно, что прямая отсекает на оси ординат отрезок, равный 0, 98. Далее измеряем tg угла наклона между прямой и осью абсцисс. Он равен 0, 55. Эмпирическая формула будет y = 0, 55 x + 0, 98. Решение способом выбранных точек. На прямой берем произвольные точки M и N и находим их координаты: M(1, 0; 1, 5), N(20, 0; 12, 3). Подставляем их в равенство y = ax + b, получаем систему уравнений: Решая, находим *y = 0, 57 x + 0, 93.

Решение способом средней. Разделим все опытные точки на две группы. В первую группу войдут первые пять точек, во вторую – остальные. Пользуясь записью (4. 3) найдем невязки для точек первой группы и сумму невязок приравняем нулю (b – 1, 02)+(3 a+b– 2, 50)+(5 a+b– 3, 92)+(8 a+b– 5, 16)+(10 a+b– 6, 82) = 0 То же сделаем для точек второй группы. (14 a+b– 8, 36)+(17 a+b– 10, 74)+(20 a+b– 11, 82)+(22 a+b– 13, 64)+(24 a+b– 12, 96) = 0 Опуская скобки и приводя подобные члены, получаем: Решая эту систему, получаем: • a = 0, 565; • b = 0, 940; • y = 0, 565 x + 0, 940.

4. 2. Квадратичное приближение Если точечный график похож на параболу, то эмпирическую формулу ищем в виде квадратного трехчлена. Предположим, что приближающаяся кривая похожа на параболу симметричную относительно оси ординат. Тогда парабола примет более простой вид (4. 4) Возьмем полу квадратичную систему координат. Это такая система координат, у которой по оси абсцисс шкала квадратичная, т. е. значения делений откладываются согласно выражению , здесь m – масштаб в каких-либо единицах длины, например, в см. По оси ординат откладывается линейная шкала в соответствии с выражением

Нанесем на эту систему координат опытные точки. Если точки этого графика располагаются приблизительно по прямой, то это подтверждает наше предположение, что зависимость y от x хорошо выражается функцией вида (4. 4). Для отыскания коэффициентов a и b можно теперь применить один из рассмотренных выше способов: способ натянутой нити, способ выбранных точек или способ средней. Способ натянутой нити применяется также, как и для линейной функции. Способ выбранных точек можем применить так. На прямолинейном графике возьмем две точки (далекие друг от друга). Координаты этих точек обозначим и (x, y). Тогда можем записать

Из приведенной системы двух уравнений найдем a и b и подставим их в формулу (4. 4) и получим окончательный вид эмпирической формулы. Можно и не строить прямолинейного графика, а взять числа , (x, y) прямо из таблицы. Однако полученная при таком выборе точек формула будет менее точна. Процесс преобразования криволинейного графика в прямолинейный называется выравниванием. Способ средней. Он применяется аналогично как в случае с линейной зависимостью. Разбиваем опытные точки на две группы с одинаковым (или почти одинаковым) числом точек в каждой группе. Равенство (4. 4) перепишем так (4. 5) Находим сумму невязок для точек первой группы и приравниваем нулю. То же делаем для точек второй группы. Получим два уравнения с неизвестными a и b. Решая систему уравнений, найдем a и b.

Заметим, что применении этого способа не требуется строить приближающую прямую. Точечный график в полу квадратичной системе координат нужен только для проверки того, что функция вида (4. 4) подходит для эмпирической формулы. Пример. При исследовании влияния температуры на ход хронометра получены следующие результаты: z -20 -15, 4 -9, 0 -5, 4 -0, 6 +4, 8 +9, 4 w 2, 6 2, 01 1, 34 1, 08 0, 94 1, 06 1, 25 При этом нас интересует не сама температура, а ее отклонение от 25. Поэтому за аргумент примем , где t – температура в градусах Цельсия обычной шкалы. Нанеся на декартову систему координат соответствующие точки, замечаем, что за приближающую кривую можно принять параболу с осью, параллельной оси ординат (рис. 4).
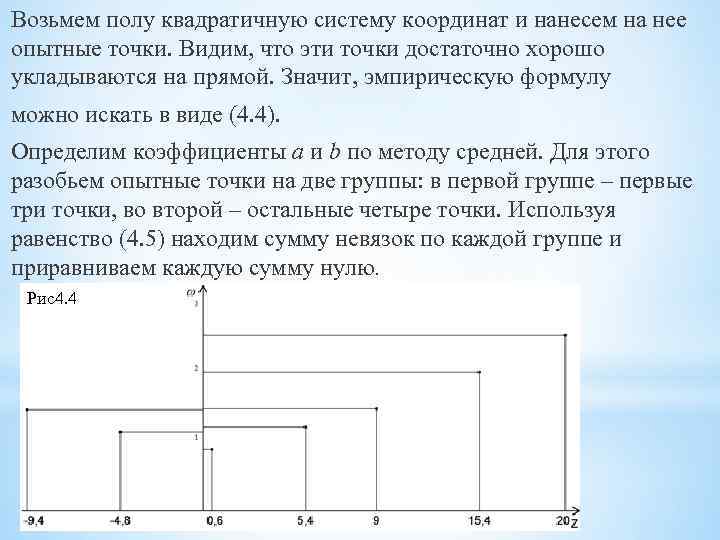
Возьмем полу квадратичную систему координат и нанесем на нее опытные точки. Видим, что эти точки достаточно хорошо укладываются на прямой. Значит, эмпирическую формулу можно искать в виде (4. 4). Определим коэффициенты a и b по методу средней. Для этого разобьем опытные точки на две группы: в первой группе – первые три точки, во второй – остальные четыре точки. Используя равенство (4. 5) находим сумму невязок по каждой группе и приравниваем каждую сумму нулю. Рис4. 4
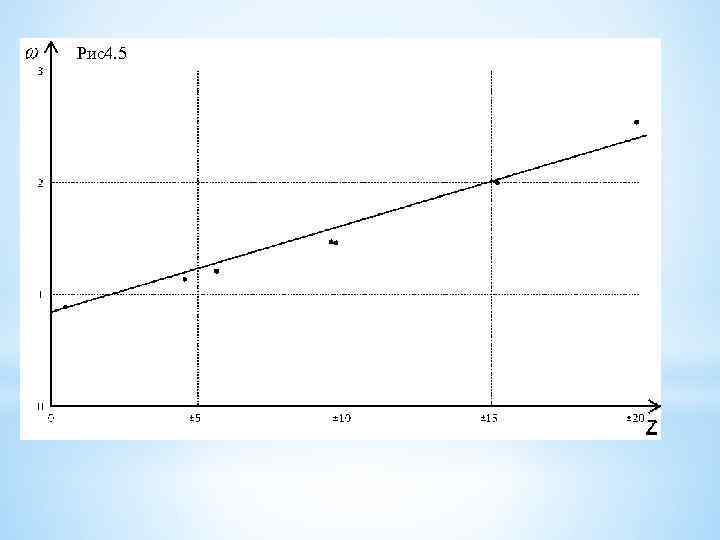
Рис4. 5

400 a+b– 2, 60+237, 16 a+b– 2, 01+81 a+b– 1, 94 = 718, 16+3 b = 6, 04. 29, 16 a+b– 1, 08+0, 36 a+b– 0, 94+23, 04 a+b– 1, 06+88, 36 a+b– 1, 25=140, 92 a+4 b=4, 33. В результате имеем такую систему уравнений Решая эту систему, получим такую эмпирическую формулу

4. 3. Приближение при помощи показательной функции Если расположение опытных точек похоже на расположение точек графика показательной функции, то ищем эмпирическую формулу в виде (4. 6) Если нанесем опытные точки на полулогарифмическую бумагу и они расположатся приблизительно на прямой линии, то мы окончательно убедимся в том, что зависимость y(x) выражается именно показательной функцией. Для нахождения A и k можно применить метод выбранных точек. Для этого прологарифмируем равенство (4. 6).

приходим к уравнению (4. 7) Зависимость (4. 7) – это линейная функция. Для отыскания a и b можно применить один из рассмотренных выше способов. Но лучше всего воспользоваться методом средней (труднее ошибиться). В уравнении (4. 7) возвратимся к старым переменным х и у и запишем его в виде ах + b – lg y = 0 (4. 8) Делим все опытные точки на две группы и для каждой группы сумму невязок уравнения (4. 8) приравниваем 0. Получаем систему двух уравнений с неизвестными а и b. Найдя а и b, находим А и k.

Пример. На основании опытных данных результаты разрядки конденсатора U(t) даются таблицей 3. t 0 1 2 3 4 5 6 7 8 9 10 U 100 75 55 40 30 20 15 10 10 5 5 Если бы мы построили опытные точки на полулогарифмической бумаге, то убедились бы, что они располагаются приблизительно на прямой. Значит зависимость U(t) можно выразить формулой (4. 6). Воспользуемся методом средней. Для этого равенство (4. 8) запишем через переменные U и t at + b – lg U = 0.

Здесь, как и прежде b = lg A, a = k lg e. Разбиваем все опытные точки на две группы. В первую группу включаем первые шесть точек, во вторую – остальные пять точек. Найдём сумму невязок в первой группе и во второй группе и приравняем их к 0 b – lg 100 + a + b – lg 75 + 2 a + b – lg 55 + 3 a + b – lg 40 + 4 a + b – lg 30 + +5 a + b – lg 20 = 15 a + 6 b = 10. 6 a + b – lg 15 + 7 a +b – lg 10 + 8 a+ b – lg 10 + 9 a +b – lg 5 + 10 a + b – lg 5 = =40 a + 5 b = 4, 57. После приведения всех подобных, получаем систему двух уравнений 80 – 48 b + 15 b = 13, 71; 33 b = 66, 3. b = 2, 01
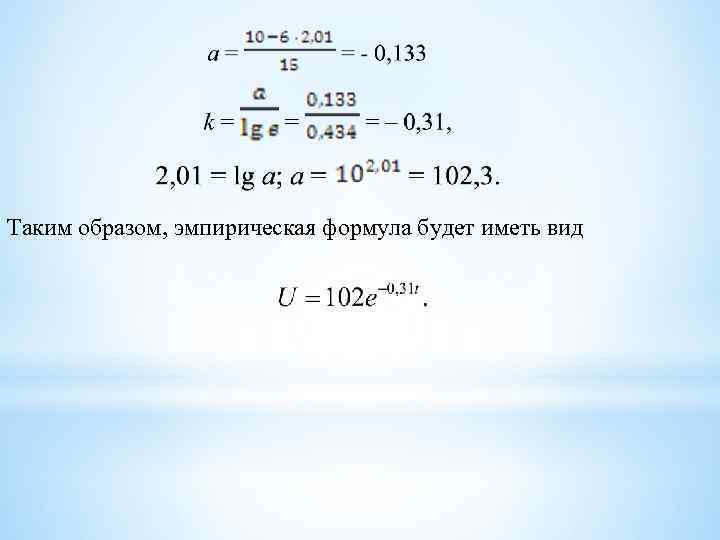
Таким образом, эмпирическая формула будет иметь вид

4. 4. Приближение при помощи степенной функции При изучении многих явлений эмпирическую формулу удобно представить в виде степенной функции. (4. 9) Признаком того, что именно такая функция выражает зависимость между данными величинами, является расположение опытных точек по прямой линии в логарифмической системе координат. Пример. Даны табличные значения x и y х 10 20 30 40 50 60 70 80 у 1, 06 1, 33 1, 52 1, 68 1, 81 1, 91 2, 01 2, 11

Не трудно предположить, что они соответствуют формуле (4. 9). Действительно, если данные точки нанести на логарифмическую систему координат, то они с достаточной точностью располагаются на прямой линии. Тем самым подтверждается наше предположение, что зависимость у(х) соответствует выражению (4. 9). Для определения параметров а и выберем крайней точки А(10; 1, 06) и В(80; 2, 11). Логарифмируя выражение (4. 9), получим Представляя координаты точек А и В, находим

Отсюда –α + 0, 0253 = – 1, 90312 + 0, 3243; 0, 9031 α = 0, 2990 α= = 0, 3311. lg A = 0, 0253 – 0, 3311 = – 0, 3058, A = 10 -0, 3058 = 0, 4945. Таким образом, Таблица проверки: х 10 20 30 40 50 60 70 80 у 1, 06 1, 33 1, 52 1, 68 1, 92 2, 01 2, 11 Сравнивая исходную таблицу с таблицей проверки, построенной по полученной эмпирической формуле, видим, что они практически совпадают.

4. 5. Способ наименьших квадратов В этом способе в качестве приближающей функции используется полином. Согласно этому способу за меру отклонения полинома Qm (x) = a 0 + a 1 x + … + amxm (10) от данной функции f(x) на множестве точек x 0, x 1, …, xn принимают величину Sm = Qm(xi) – f(xi)]2. Очевидно, что Sm есть функция коэффициента а 0, а 1, …, аm. Эти коэффициенты надо подобрать так, чтобы величина Sm была наименьшей. Для решения этой задачи найдём частные производные от величины Sm = a 0 + a 1 xi + a 2 xi 2 + … + amxim – yi)2.

Приравнивая эти частные производные к 0, получим для определения неизвестных a 0, a 1, …, am систему m+1 уравнений с m+1 неизвестными.

Здесь производная берётся от сложной функции, т. е Введём обозначения где S 0 = n+1.

Можно доказать, что если среди точек х0, х1, …, хn нет совпадающих и m ≤ n, то определителем системы (4. 12) ≠ 0 и следовательно эта система имеет единственное решение Полином (4. 10) с такими коэффициентами будет обладать минимальным квадратным отклонением.
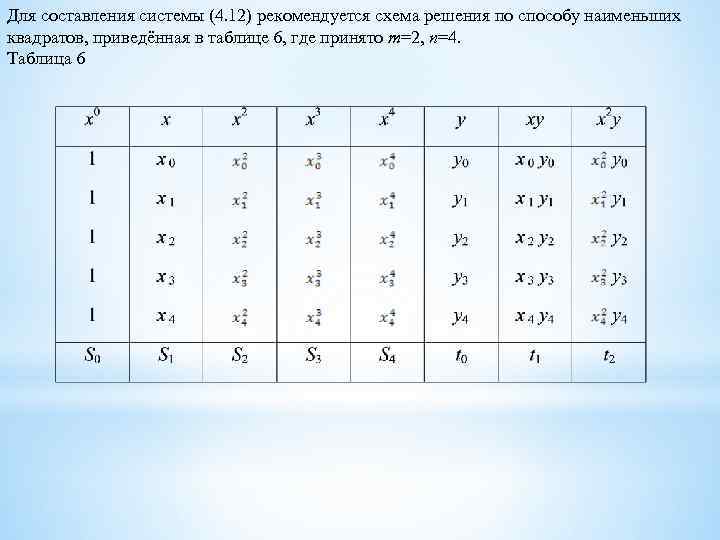
Для составления системы (4. 12) рекомендуется схема решения по способу наименьших квадратов, приведённая в таблице 6, где принято m=2, n=4. Таблица 6
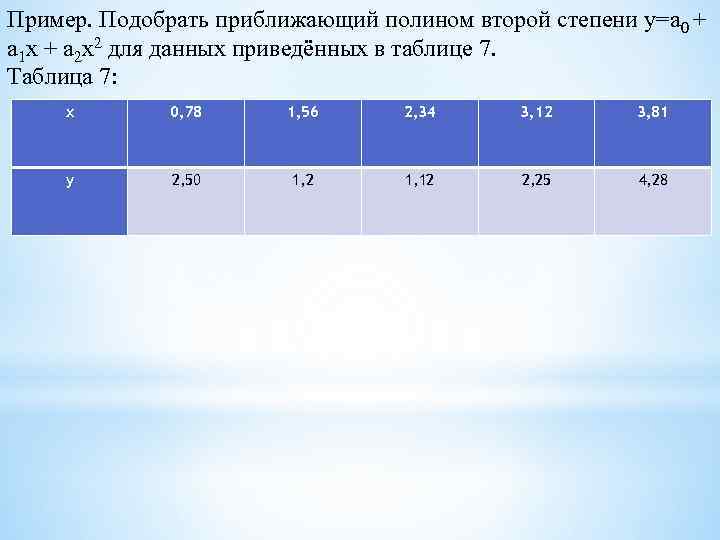
Пример. Подобрать приближающий полином второй степени y=a 0 + a 1 x + a 2 x 2 для данных приведённых в таблице 7. Таблица 7: x 0, 78 1, 56 2, 34 3, 12 3, 81 y 2, 50 1, 2 1, 12 2, 25 4, 28
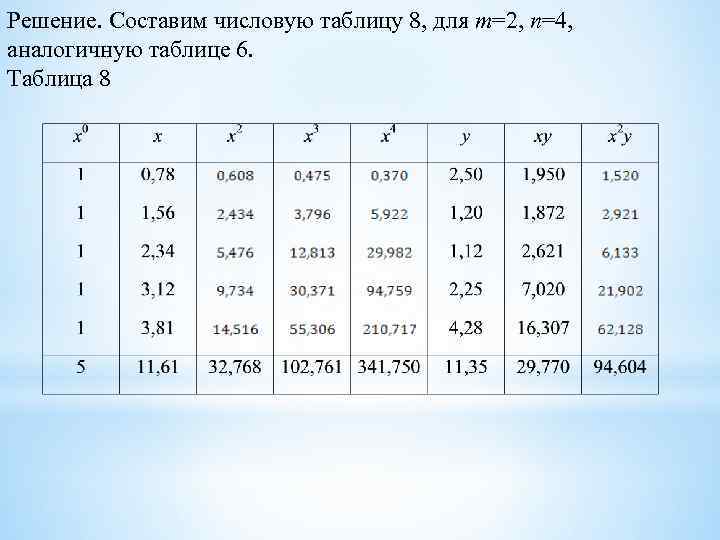
Решение. Составим числовую таблицу 8, для m=2, n=4, аналогичную таблице 6. Таблица 8

Отсюда система (4. 12) для определения коэффициентов a 0, a 1, a 2 примет вид Решив эту систему, будем иметь a 0=5, 045, a 2=1, 009. Следовательно, искомый полином будет иметь следующий вид y = 5, 045 – 4, 043 х + 1, 009 х2.

4. 6. Некоторые соображения о выборе вида эмпирической формулы с двумя параметрами Если задана какая-то таблица с экспериментальными данными xj и yj и нет никакой дополнительной информации, то определение вида эмпирической формулы представляет собой трудную задачу. Рассмотрим сначала случай, когда эмпирическая зависимость определяется формулой с двумя параметрами a и b, то есть y = f (x; a, b) (4. 13) Если окажется, что (4. 14) то искомая зависимость линейная, т. е. y = ax + b 1 и задача легко решается. (4. 15)

Другим простым случаем является определение квадратичной зависимости y = ax 2 + b (4. 16) путём построения графика на полу квадратической системе координат, на которой парабола (4. 16) представляется прямой линией, а коэффициенты a и b легко находятся рассмотренными выше способами Рассмотрим общий случай, когда соотношение (4. 13) не сводиться к формулам (4. 15) и (4. 16). Получим необходимое условие существования эмпирической зависимости вида (4. 13) для заданной системы точек (xi, yi). Пусть Mi(xi, yi), Mj(xj, yj), Mk(xk, yk) три точки значений из нашей совокупности. Предполагая, что кривая (4. 13) проходит через точки Mi, Mj и Mk, будем иметь yi = f(xi; a, b), yj = f(xj; a, b), yk = f(xk; a, b) (4. 17) Исключая из системы (4. 17) параметры a и b, получим соотношение вида Ф(xi, xj, xk, yi, yj, yk) = 0. (4. 18)

Выполнение равенства (4. 18) для любых значений необходимо для существования зависимости (4/13). Проверка соотношения (4. 18) связана с трудоёмкими вычислениями, поэтому на практике ограничиваются одной тройкой точек: начальной (x 1, y 1), промежуточной (x. S, y. S) и конечной (xn, yn). Точку MS выбирают так, чтобы соотношение (4. 18) было по возможности простым. Иногда точку MS выгодно брать не принадлежащую нашему ряду точек, тогда координаты x. S, y. S определяются интерполированием. Пример. Получить необходимое условие для существования степенной зависимости y = axk, (4. 19) предполагая, что xi > 0, yi > 0 (i=1, 2, …, n). Решение. Выберем Из формулы (4. 19) имеем

Исключая из соотношения (4. 20) параметры a и b получим а от сюда следует, что Таким образом, для существования степенной зависимости (4. 19) необходимо, чтобы среднему геометрическому x. S значений х1 и хn соответствовало среднее геометрическое y. S значение y 1 и yn. Если x. S не является табличным, то соответствующее значение y. S определяется с помощью интерполирования. Далее мы рассмотрим наиболее часто встречающиеся зависимости.

Аналогично тому как это было сделано выше в примере для существования зависимостей 1– 7 можно вывести простые необходимые условия: При этом предполагается, что хi > 0 и уi > 0. Эти выражения для приведены в таблице 9.

Приведённая таблица 9 облегчает выбор эмпирической формулы среди указанных. Для проверки пригодности определённой эмпирической формулы, пользуясь исходными данными, находим значение и табличное значение и сравниваем его со значением Предпочтительнее та формула, для которой расхождение наименьшее. Если значение не находятся среди исходных данных xi, то отвечающее ему значение можно определить посредством линейной интерпретации

Следует иметь ввиду, что описанный подход является грубо ориентированным, так как мы не учитываем поведение всех промежуточных точек ( ). Кроме того, приведённая таблица эмпирических функций охватывает небольшое количество зависимостей и может случиться, что переменные х и у подчинятся некоторой закономерности, не вошедшей в наш список. Следует так же учесть, что функции 1– 7 монотонные, и, следовательно отвечающие им упорядоченные данные ( ) при ∆xi = xi+1 – xi > 0 (i = 1, 2, …, n-1), должны обладать постоянным знаком приращения Если это условие не выполняется, то зависимости 1– 7 не могут использоваться в качестве эмпирических формул. Пример. Определить вид эмпирической формулы, отвечающей следующей таблице 10.

Таблица 9

Таблица 10: х 273 288 293 313 333 353 373 у 29, 4 33, 3 35, 2 37, 2 45, 8 55, 2 65, 6 77, 3 Решение. Будем искать эмпирическую формулу среди зависимостей 1– 7, приведённых в таблице 9. Результаты вычислений приведены в таблице 11, из которой следует, что нужно выбрать степенную зависимость y = axb.

Таблица 11

4. 7. Эмпирические формулы, содержащие три параметра. В этом случае эмпирические формулы в общем виде записываются так y = f(x; a, b, c), где a, b и с – некоторые постоянные. Первой формулой с тремя параметрами является квадратическая зависимость y= ax 2 + bx + c. (4. 21) Критерий проверки экспериментальных данных на зависимость (4. 21) существует. Но он строится с таки громоздкими расчётами и составлением сложной таблицы, что легче по экспериментальным данным построить кривую, как мы это уже делали, и убедиться, похожа ли она на зависимость (4. 21). Рассмотрим степенную зависимость вида y = axb + c (4. 22)

Отсюда y – c = axb. Логарифмируя это выражение получим lg (y – c) = lg a +b lg x. Полагая lg (y - c) = Y и lg x = X, получим линейную зависимость Y =X b + lg a. Определение параметров формулы (4. 22) начнём с нахождения с. Для этого составим среднее геометрическое и, пользуясь графиком, построенным по исходным данным, или методом линейной интерполяции для Предполагая, что точки M 1(x 1, y 1), MS(x. S, y. S), Mn(xn, yn) расположены на кривой (4. 22), будем иметь три неравенства.

Возводя в степень b и умножая на а, получим После этого строим точки Ni(Xi, Yi) , где Xi = lg xi, Yi = lg(yi – c) (i = 1, 2, …, n). Если эти точки располагаются близко к прямой линии, то зависимость (4. 22) выбрана правильно. Причём, постоянные а и b находятся обычным способом. Пример. Для переменных х и у дана таблица 12 х 50 500 900 1200 1600 2000 у 0, 10 0, 28 0, 80 1, 38 2, 56 4, 10

Таблица 12 х 250 500 900 1200 1600 2000 у 0, 10 0, 28 0, 80 1, 38 2, 56 4, 10 Найти эмпирическую формулу, связывающую эти переменные коэффициентами a, b и с. Решение. Построим эмпирическую формулу вида: y = axb + c. Находим На графике, если его построить, этому значению соответствует Отсюда

Остальные параметры а и b найдём методом средних. Составляем начальное уравнение с учетом, найденного значения с. lg (yi – 0, 048) = lg a + b lg xi, (i = 1, 2, …, 6) Тогда будем иметь систему уравнений -1, 2840 = lg a+ 2, 3979 b; 0, 1245 = lg a + 3, 0792 b; -0, 6345 = lg a + 2, 6990 b; 0, 4000 = lg a + 3, 2041 b; -0, 1238 = lg a + 2, 9542 b; 0, 6077 = lg a + 3, 3010 b; Группируя эти уравнения по три, получим

Таким образом, искомая эмпирическая формула будет иметь вид. y = 5, 75 · 10 -7 x 2, 071 + 0, 048. Рассмотрим показательную зависимость y = aebx + c (4. 23) Перенося слагаемое с влево и логарифмируя, получим lg (y - c) = lg a + bx. M, где M = lg e = 0, 434.

Таким образом, Y = lg a + b. Mx, (4. 24) где y = lg(y – c). Определим параметр с. Для этого, как и в предыдущем случае, выберем крайние точки M 1(x 1, y 1) и Mn(xn, yn) и составим среднее арифметическое Для найдём соответствующее У (или из чертежа, или линейной интерполяцией). Представляя эти значения в эмпирическую формулу (4. 23), будем иметь

Следовательно Получим точно такое же уравнение, как и в предыдущем случае. Поэтому с запишем в таком же виде

Если обнаружена линейная зависимость (4. 24), то остальные параметры а и b находятся обычными приёмами. Пример. Дана таблица 13 х 0 Таблица 13 0, 1 0, 2 0, 3 0, 4 0, 5 0, 6 0, 7 0, 8 0, 9 у 1, 3 1, 4 1, 5 1, 7 1, 9 2, 1 2, 4 2, 7 3, 0 3, 4 Найти эмпирическую формулу. Будем её искать в виде y = aebx + c. сначала найдём Этому значению Отсюда в данной таблице соответствует значение 1, 0 3, 8

Параметры а и b определяем по методу средних. Для этого запишем lg (yi – 0. 258) = lg a + b. Mxi, (i = 1, 2, …, 10). Составим две системы уравнений Подставив значения xi и yi и приведя подобные члены, получим систему двух уравнений Решая эту систему найдём: а = 1, 044; b = 1, 234. Следовательно, эмпирическая формула имеет вид у = 1, 044 е 1, 234 х+0, 258.

• Библиографический список • Бахвалов Н. С. и др. Численные методы. -М. : - СПб. Физматлит 2001. – 632 с. • Кунцман Ж. Численные методы. -М. : Изд-во Наука, 1979. • Бахвалов Н. С. и др. Численные методы в задачах и примерах. – М. : Высшая школа, 2000. • Волков Е. А. Численные методы, – М. : Изд-во Наука, 1987. • Калиткин Н. Н. Численные методы. –М. : Изд-во Наука, 1978. – 512 с. • Демидович Б. П. , Марон И. А. Основы вычислительной математики. -М. : Изд-во Наука, 1970. -664 с. • Гуттер Р. С. , Овчинский Б. В. Элементы численного анализа и математической обработки результатов опыта. –М. : Изд-во Наука, 1970. – 432 с.
Данильченко.Лекции.часть 3.pptx