ПРЕЗЕНТАЦІЯ УРОКУ КВАДРАТ ДВОЧЛЕНА Підготувала

ПРЕЗЕНТАЦІЯ УРОКУ « КВАДРАТ ДВОЧЛЕНА » Підготувала Гончарова Світлана Вікторівна, учитель математики ДЗОШ № 126 І-ІІІ ступенів

ТЕМА КВАДРАТ СУМИ І КВАДРАТ РІЗНИЦІ ДВОХ ВЫРАЗІВ УРОКУ

МЕТА УРОКУ: Освітня : -вивести формули квадратів суми і різниці двох виразів ; -сформувати вміння учнів практично застосовувати ці формули для спрощення виразів, раціонального обчислення числових виразів. Развиваюча : -развинути логічне мислення, увагу , пам’ять, кмітливість, культуру математичної мови і культуру спілкування. Виховна : -виховувати відповідальне відношення до діяльності, високої пізнавательної активності та самостійності; -виховувати інтерес до математики як навчального предмету крізь сучасні технології викладання; - Виховувати почуття відповідальності. культуры диалога.

План уроку Організаційний момент. Актуалізація опорних знань (усна робота). Вивчення нового матеріалу (дослідницька робота). Первичне закріплення. Геометричний смысл формул квадрата суми. Закріплення вивченого матеріалу. Перевірка засвоення вивченого матеріалу (первічний контроль знань ). Домашне завдання. Підсумок уроку.

Епиграф уроку: Знання тільки тоді знання, коли воно придбане зусиллями своєї думки, а ні пам’яттю. (Л. М. Толстой)

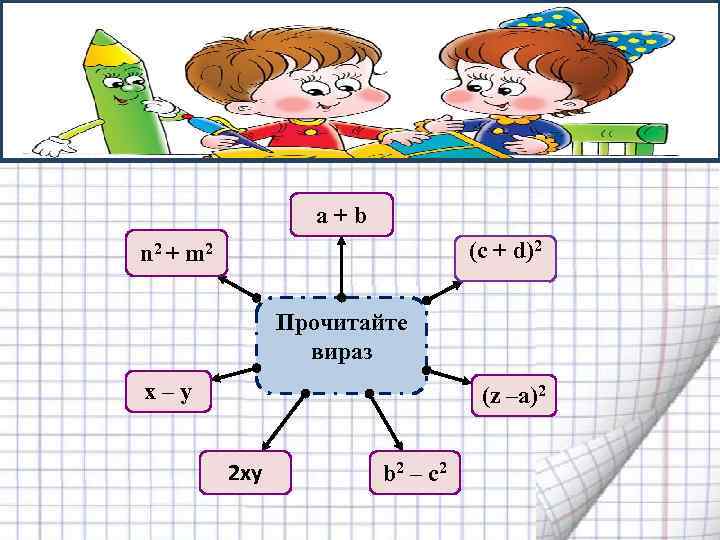а + b (c + d)2 n 2 + m 2 Прочитайте вираз x – у (z –a)2 2 ху b 2 – c 2

a - 2 Знайдіть квадрати виразів 5 b 4 х2 6 х2 у3

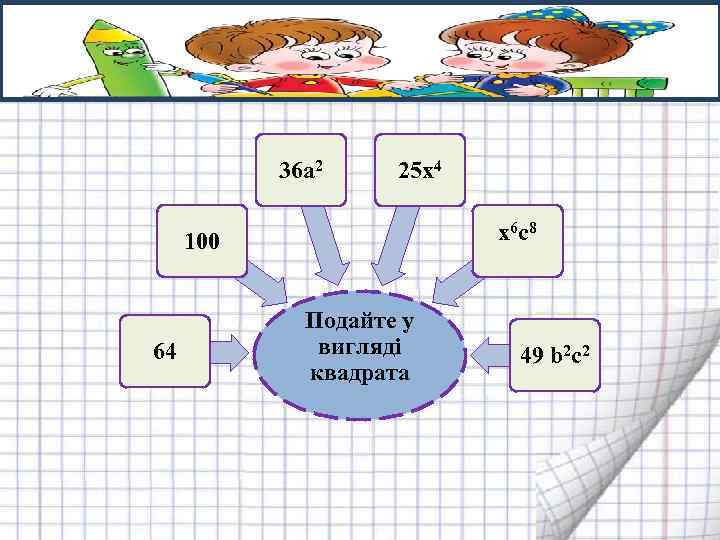36 а 2 25 x 4 х6 с8 100 64 Подайте у вигляді квадрата 49 b 2 c 2

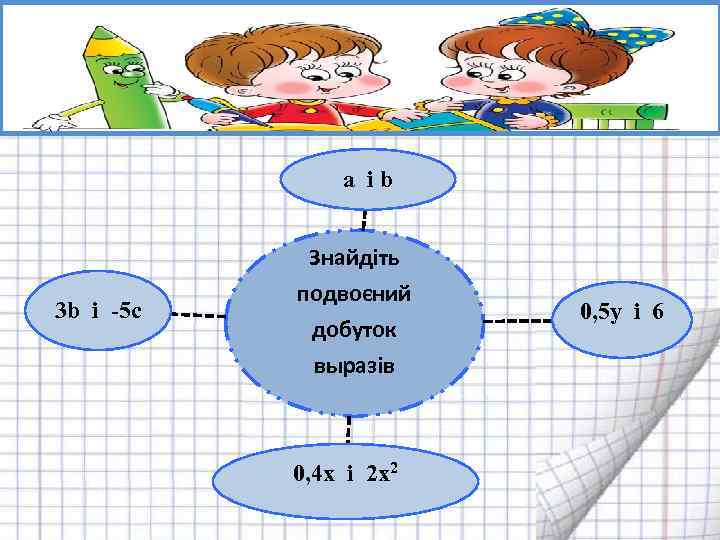а і b 3 b і -5 с Знайдіть подвоєний добуток выразів 0, 4 х і 2 х2 0, 5 y і 6

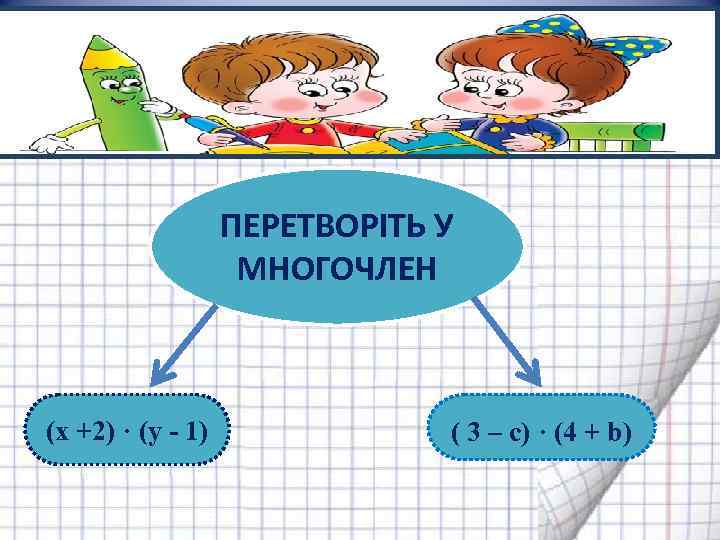ПЕРЕТВОРІТЬ У МНОГОЧЛЕН (x +2) · (y - 1) ( 3 – c) · (4 + b)

СПРОСТІТЬ ВИРАЗ 1 вариант • (y + b) (y +b) • (с + d ) (c +d) • (х + 2) (х+2) 2 вариант • (x – y) • (m - n) (m- n) • (a – 2)

ДОСЛІДНИЦЬКА РОБОТА № I II (y + b) 2 (c + d)2 (х + 2)2 III y 2 + 2 yb + b 2 c 2 + 2 cd + d 2 х2 + 4 х + 4 x 2 – 2 xy + y 2 m 2 – 2 mn + n 2 a 2 – 4 a + 4 1. (y + b) (y +b) 2. (с + d ) (c +d) 3. (х + 2)(х+2) 4. (x – y) 5. (m - n) (m- n) (x – y)2 (m - n)2 6. (a – 2)2

ПЕРЕВІРКА (6 х + y) 2 = 36 х2 + 12 xy + y 2 ( (5 - 4 b) 2 = 25 - 40 b + 16 b 2

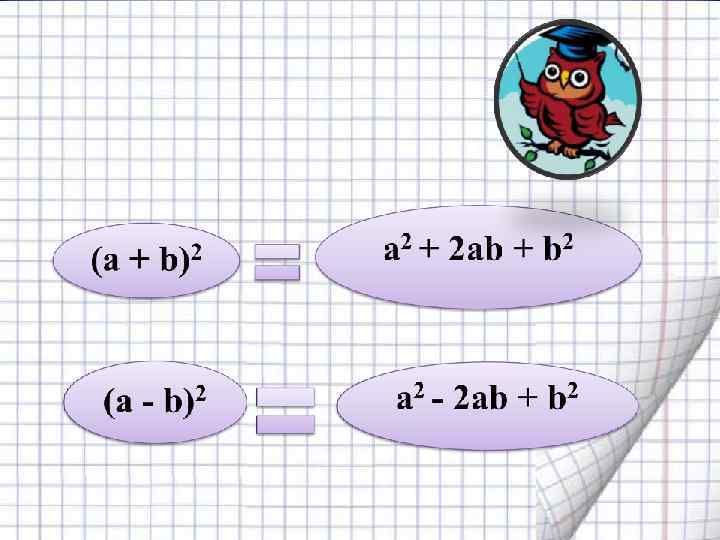
(а + b)2 =а 2 + 2 аb +b 2 Квадрат суми двох виразів дорівнює (а - b)2 =а 2 - 2 аb+b 2 Квадрат різниці двох виразів дорівнює квадрату першого виразу без плюс подвоєний першого на другий подвоєного добутка першого на другий вираз добуток плюс квадрат другого виразу

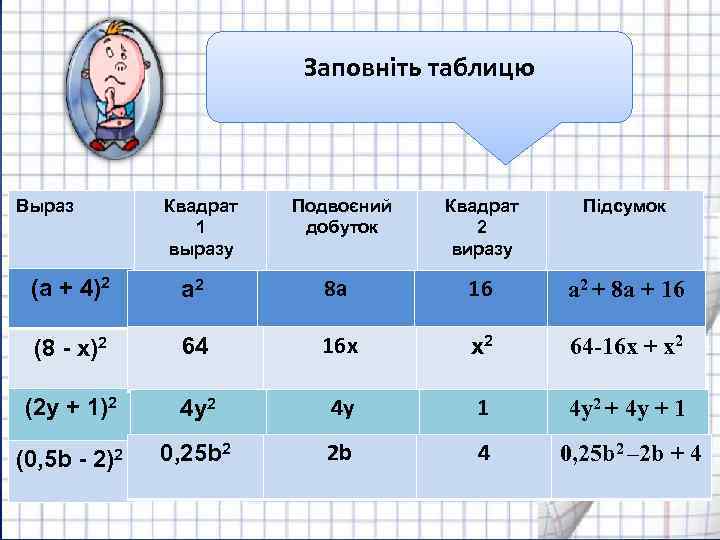Заповніть таблицю Выраз Квадрат 1 выразу Подвоєний добуток Квадрат 2 виразу Підсумок (а + 4)2 а 2 8 а 16 а 2 + 8 а + 16 (8 - х)2 64 16 х х2 64 -16 х + х2 (2 y + 1)2 4 у 1 4 у2 + 4 у + 1 (0, 5 b - 2)2 0, 25 b 2 2 b 4 0, 25 b 2 – 2 b + 4

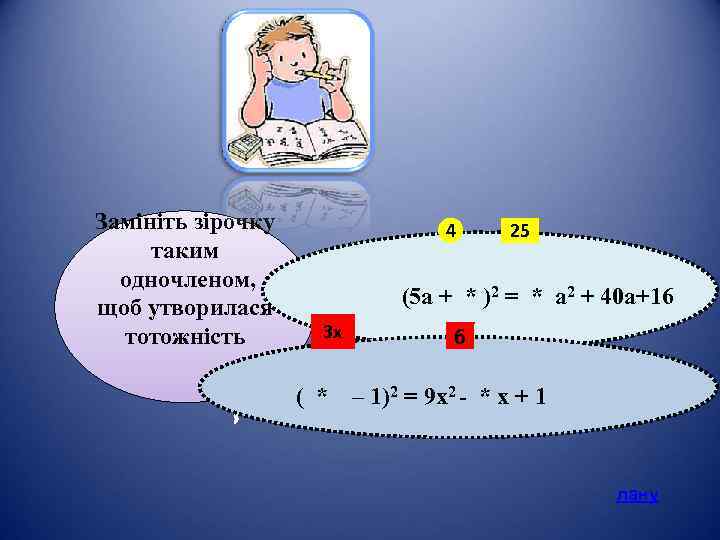Замініть зірочку таким одночленом, щоб утворилася тотожність , 4 25 (5 а + * )2 = * а 2 + 40 а+16 3 х 6 ( * – 1)2 = 9 х2 - * х + 1 лану

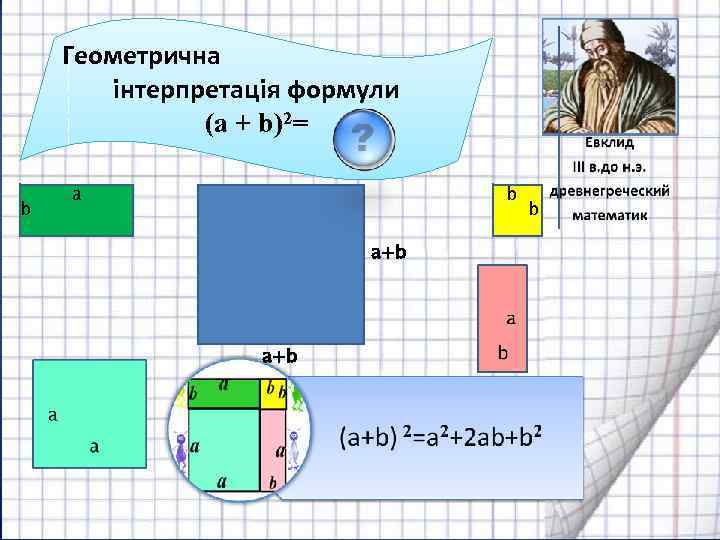Геометрична інтерпретація формули (a + b)2= b a+b a+b b

1. Обчисліть: (30+1) 2 (30 -1) 2 512 492 2. Подайте у вигляді многочлена вираз : (а-7) 2 ( 5+х) 2 (7 -а) 2 (-5 -х) 2

ПЕРЕВІРКА

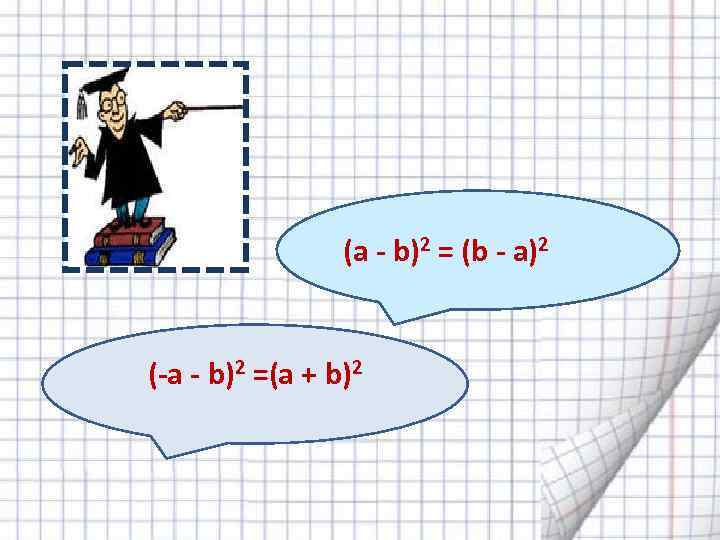(а - b)2 = (b - а)2 (-а - b)2 =(а + b)2

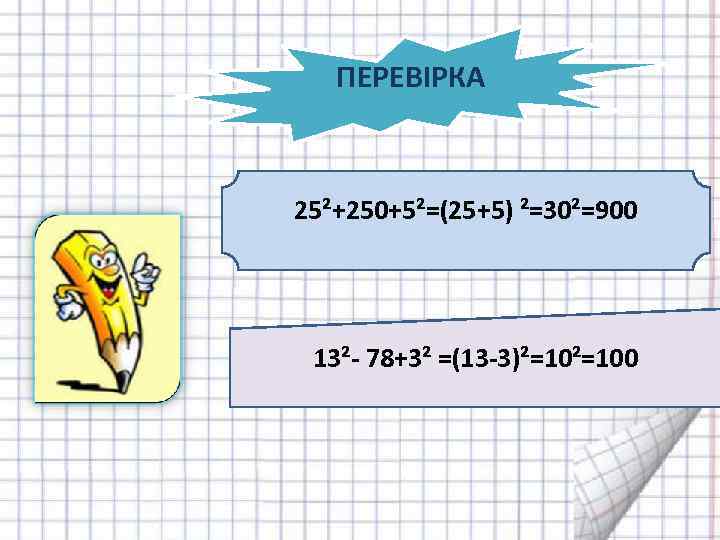ПЕРЕВІРКА 25²+250+5²=(25+5) ²=30²=900 13²- 78+3² =(13 -3)²=100

1. ( 3 а + с) 2 2. ( а -2 в) 2 3. ( x – в) 2 4. y 2 -2 yв + в 2 5. ( y - в) 2 6. 9 а 2+ 6 ас + с2 2 2 7. а 2 - 4 ав + 4 в 2 8. x 2– 2 xв + в 2

(y - 9)2 y 2 -9 y +81 (5 x+4 y)2 (2 a – 0, 5 x)2 25 x 2 - 20 xy +16 y 2 4 a 2 - 2 ax +0, 25 x 2 y 2 + 18 y +81 25 x 2 +40 xy +16 y 2 4 a 2 + 2 ax +0, 25 x 2 y 2 -18 y +81 25 x 2 +20 xy +16 y 2 4 a 2 - ax +0, 25 x 2 y 2 + 9 y +81 25 x 2 - 40 xy +16 y 2 4 a 2 + ax +0, 25 x 2

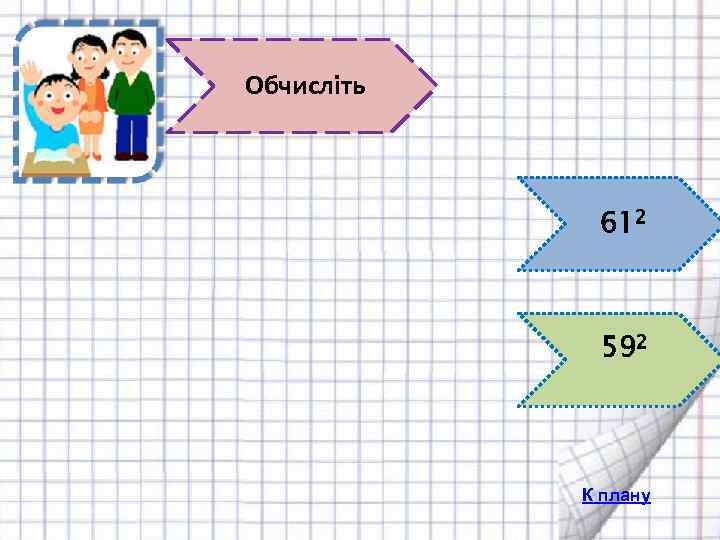Обчисліть 612 592 К плану

Домашне завдання. § 16, № 591; № 593 ; № 599; № 604.

-З якими формулами ми познайомилися сьогодні на уроці ? - Чому ці формули називають формулами скороченого множення? - Чому дорівнює квадрат суми двох виразів ? - Чому дорівнює квадрат різниці двох виразів ? Виставлення оцінок.