Презентация СА practice 2 var

Скачать презентацию СА practice 2 var Скачать презентацию СА practice 2 var

sa_practice_2_var.ppt

  • Размер: 726 Кб
  • Количество слайдов: 16

Описание презентации Презентация СА practice 2 var по слайдам

При клади до за в дан ня 2 При клади до за в дан ня

Приклад 1: Завдання протидії. Задані цільові функції супротивників, також множина стратегій кожного з них: Далі ставитимемоПриклад 1: Завдання протидії. Задані цільові функції супротивників, також множина стратегій кожного з них: Далі ставитимемо завдання, які пропонується вирішити як контрольні, і вирішувати їх з докладними поясненнями. 4; 01 226, 842, 2 21 2 12121 2 2 21 2 12112 xx xxxxxxf

1. Визначити гарантовані результати супротивників табличним методом, при цьому кроки сітки по стратегіях обох супротивників 1. Визначити гарантовані результати супротивників табличним методом, при цьому кроки сітки по стратегіях обох супротивників вважати рівними 1 (крок сітки вибраний великим в порівнянні з варіантами, що пропонується вирішити самостійно, але даний приклад носить показовий характер, при вирішенні контрольних завдань вказаний алгоритм треба буде програмувати).

Рішення: гарантований результат визначається за допомогою таблиць досить просто за принципом max min Рішення: гарантований результат визначається за допомогою таблиць досить просто за принципом max min : Для функції f 12 ( x 1 , x 2 ) x 1 0 x 2 0 1 2 3 4 f

x 1 1 x 2 0 1 2 3 4 f 12 9 6 5 6x 1 1 x 2 0 1 2 3 4 f 12 9 6 5 6 9 x 1 2 x 2 0 1 2 3 4 f 12 8 5 4 5 8 x 1 3 x 2 0 1 2 3 4 f 12 5 2 1 2 5 x 1 4 x 2 0 1 2 3 4 f 12 0 -3 -4 —

З таблиці видно, що 52112 21 ; , minmaxfxxf xx З таблиці видно, що 52112 21 ; , minmaxfxxf xx

Знаходження гарантованого результату f 21* x 2 0 x 1 0 1 2 3 Знаходження гарантованого результату f 21* x 2 0 x 1 0 1 2 3 4 f 21 2 -3 -6 -7 —

x 2 1 x 1 0 1 2 3 4 f 21 3 -2 -5 -6x 2 1 x 1 0 1 2 3 4 f 21 3 -2 -5 -6 -5 x 2 2 x 1 0 1 2 3 4 f 21 2 -3 -6 -7 -6 x 2 3 x 1 0 1 2 3 4 f 21 -1 -6 -9 -10 -9 x 2 4 x 1 0 1 2 3 4 f 21 -1 -6 -14 — 15 —

З таблиці виходить, що f 21 * = Тепер визначимо гарантовані результати класичним З таблиці виходить, що f 21 * = Тепер визначимо гарантовані результати класичним методом, що базується на дослідженні екстремальних властивостей функцій. 61; 3, minmax * 212121 12 fxxf x x

Проведемо дослідження функції f 12 ( x 1 , x 2 ) з даної умови Проведемо дослідження функції f 12 ( x 1 , x 2 ) з даної умови отримуємо, що мінімум досягається при x 2 =2. Тепер необхідно знайти значення x 1 , при якому наша функція досягатиме максимуму. 0422 2 12 x x f

У f 12 ( x 1 , x 2 ) підставимо знайдене значення x 2 У f 12 ( x 1 , x 2 ) підставимо знайдене значення x 2 =2. Візьмемо похідну по x 1 і прирівняємо нулю: звідки виходить, що x 1 =1. З характеру функції знову виходить, що в крапці x 1 =1 будет максимум 0222 1 1 112 x x xf ), (

Отже, ми отримали, що Те ж саме, але вже без пояснення виконаємо для другого гравця, Отже, ми отримали, що Те ж саме, але вже без пояснення виконаємо для другого гравця, тобто для функції f 21 ( x 1 , x 2 ) 52; 1, minmax * 122112 2 1 fxxf x x 062 1 1 21 x xf

Отримаємо, що в крапці x 1 =3 досягається мінімум звідки витікає, що в крапці Отримаємо, що в крапці x 1 =3 досягається мінімум звідки витікає, що в крапці x 2 =1 досягається максимум. Отже 022 3 2 2 221 x x xf), ( 61; 3, minmax * 212121* 21 12 fxxff x x

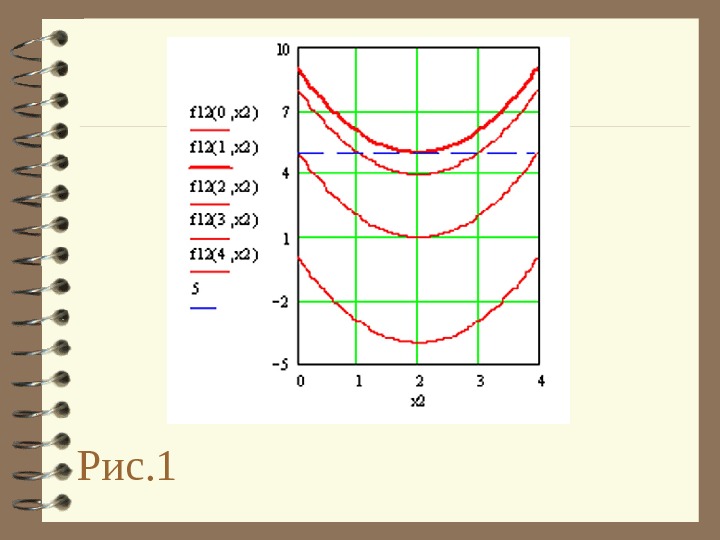
І, нарешті, для визначення f 21 * , f 12 * скористаємося графічним І, нарешті, для визначення f 21 * , f 12 * скористаємося графічним методом. Для знаходження f 12 * , фіксуючи ряд значень x 1 , будуються графіки функції f 12 ( x 1 , x 2 ) по x 2 (рис. 1).

Рис. 1 Рис.

Рис. 1. 1 Рис. 1.