ПРЕЗЕНТАЦИЯ НА ТЕМУ: ВЫПОЛНИЛА : КУЧКИНА К.

ПРЕЗЕНТАЦИЯ НА ТЕМУ: ВЫПОЛНИЛА : КУЧКИНА К. С ГРУППА ГТ-11

Пьер де Ферма ( 17 августа 1601 — 12 января 1665) — французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года — советник парламента в Тулузе. Блестящий полиглот. Наиболее известен формулировкой Великой теоремы Ферма.

Пусть функция определена на некотором промежутке Х и во внутренней точке этого промежутка имеет наибольшее или наименьшее значение. Тогда: если в точке существует конечная производная, то она равна нулю, т. е.

Дано: определена на множестве Х , - внутренняя точка, Доказать: существует конечная производная причем Доказательство: По условию, в точке функция принимает наибольшее значение на промежутке. Это означает, что По определению, причём предел не зависит от способа стремления 1) Пусть слева , тогда 2)Пусть справа , тогда Перейдём к пределам в этих неравенствах: из (1) из (2) Это возможно лишь в случае, когда Теорема доказана

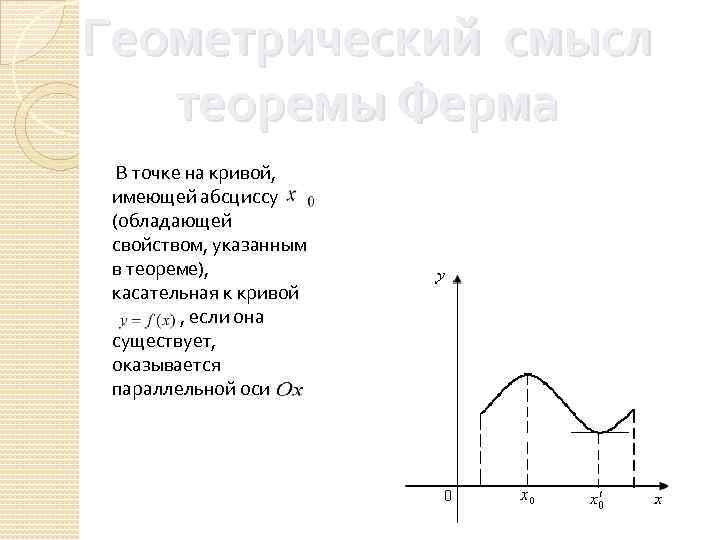
Геометрический смысл теоремы Ферма В точке на кривой, имеющей абсциссу (обладающей свойством, указанным в теореме), касательная к кривой , если она существует, оказывается параллельной оси

Мишель Ролль ( 21 апреля 1652, — 8 ноября 1719) — французский математик. Родился в городке Амбер (фр. Ambert, провинция Овернь). По прибытии в Париж, в возрасте 23 лет, он в начале добывал себе средства к существованию перепиской. Его математические способности, обнаружившиеся, между прочим, в решении трудной задачи, предложенной Озанамом, открыли ему двери академии. В 1685 году он стал её членом.

Теорема Ролля Пусть на определена функция причём 1) непрерывна на 2) На существует конечная производная 3) Тогда на отрезке существует такая точка с, в которой производная функции обращается в нуль, т. е.

Доказательство По условию , непрерывна на . Функция, непрерывная на отрезке, достигает своего наибольшего и своего наименьшего значений в некоторых точках этого отрезка.

Доказательство Пусть М- наибольшее значение функции на , т- наименьшее значение на . Тогда выполняется неравенство Если т = М , то постоянна и, значит, на . В качестве точки можно взять любую точку , и теорема доказана. Если то из условия 3) следует, что хоть одно из значений, т или М , не принимается функцией на концах отрезка Пусть Это означает, что существует внутренняя точка отрезка в которой функция принимает наибольшее значение на отрезке Тогда из теоремы Ферма следует, что Теорема доказана.

Если непрерывная кривая изображает дифференцируемую функцию, то между двумя точками, лежащими на одинаковой высоте, всегда имеется точка, в которой касательная параллельна оси . Полезный вывод: между каждыми двумя корнями дифференцируемой функции находится по крайней мере один корень её производной

Дано: Проверить, выполняется ли теорема Ролля для функции на отрезке ; при каком значении с выполняется условие Решение. Функция определена и непрерывна в каждой точке заданного отрезка. На концах отрезка значения функции равны: следовательно, теорема Ролля на этом отрезке выполняется. Значение для с определяем из условия . Найдем производную: приравняем её к нулю: То есть . Напомним, что в точке с абсциссой 2, 5 функция имеет касательную, параллельную оси абсцисс.

Жозе ф Луи Лагра нж ( 25 января 1736, Турин — 10 апреля 1813, Париж) — французский математик, астроном и механик итальянского происхожден ия. Лучший математик XVIII века. Особенно прославился исключительным мастерством в области обобщения и синтеза накопленного научного материала.

Пусть на отрезке определена функция , причём: 1) непрерывна на 2) на существует конечная производная Тогда существует точка с, такая, что выполняется условие

Введём вспомогательную функцию: Эта функция удовлетворяет всем условиям теоремы Ролля: 1) непрерывна на как разность непрерывной функции и непрерывной линейной функции ; 2) на интервале существует конечная производная 3) так как , .

Следовательно, по теореме Ролля, для функции найдётся такая точка что Но значит, Теорема доказана. Доказанное равенство называют формулой Лагранжа или формулой конечных приложений, удобнее пользоваться ею в виде: где

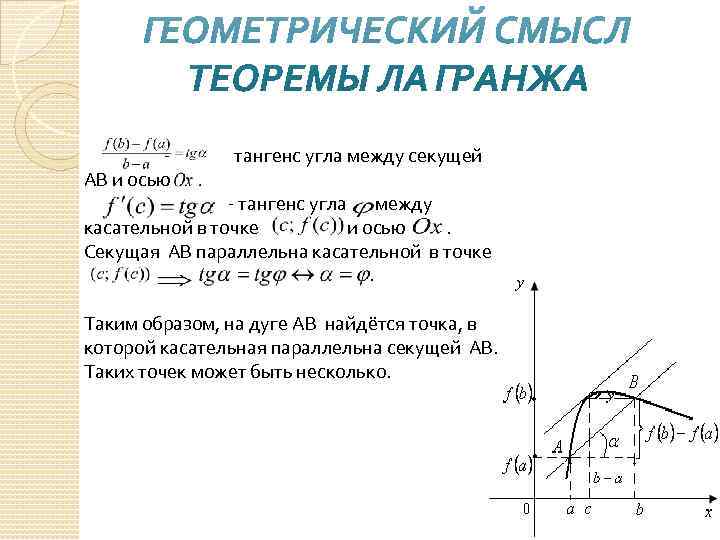
- тангенс угла между секущей АВ и осью - тангенс угла между касательной в точке и осью . Секущая АВ параллельна касательной в точке Таким образом, на дуге АВ найдётся точка, в которой касательная параллельна секущей АВ. Таких точек может быть несколько.

Напомним, что приращение - это изменение функции на отрезке ; - средняя скорость изменения функции на этом отрезке; значения же производной в точке – это мгновенная скорость изменения функции. Тогда теорема утверждает, что существуе хотя бы одна точка внутри отрезка, такая, что скорость изменения функции в ней равна средней скорости изменения функции на этом отрезке.

Если функция непрерывна на и её производная равна нулю на то функция постоянна на

Доказать, что Решение. Рассмотрим функцию. Функция непрерывна на дифференцируема на Тогда на или Так как при то Следовательно,

Огюстен Луи Коши ( 21 августа 1789, Париж — 23 мая 1857, Франция) — великий французский математик, член Парижской академии наук, Лондонского королевского общества, Петербургской академии наук и других академий. Разработал фундамент математического анализа, внёс огромный вклад в анализ, алгебру, математическую физику и многие другие области математики. Его имя внесено в список величайших учёных Франции, помещённый на первом этаже Эйфелевой башни.

Пусть на отрезке заданы функции и причём: 1) функции и непрерывны на 2) имеют производные (конечные) в каждой точке интервала 3) производная во всех точках интервала Тогда на интервале существует такая точка с, что (формула Коши)

Введём вспомогательную функцию: Функция удовлетворяет всем трём условиям теоремы Ролля: 1) непрерывна на 2) имеет на конечную производную 3) Следовательно, можно применить теорему Ролля: найдётся такая точка с, что Но значит, или Теорема доказана.

1. Если то теорема Лагранжа оказывается частным случаем теоремы Коши 2. Если в условиях теоремы Коши определить то где