 Презентация на тему: «Производная»
Презентация на тему: «Производная»
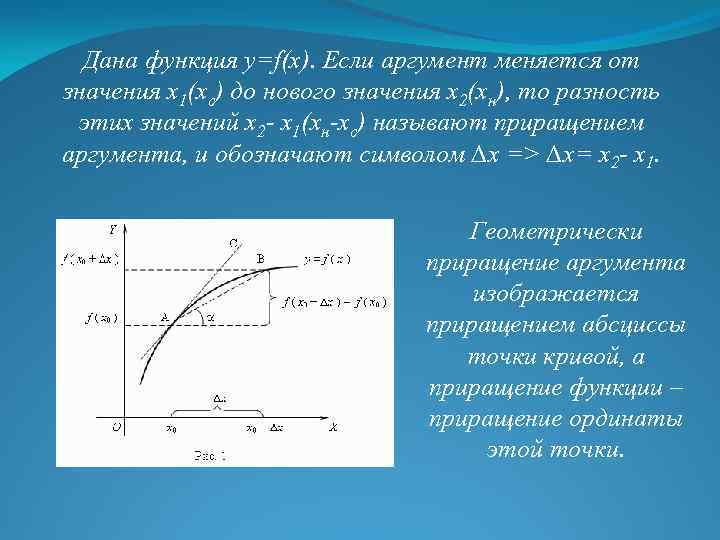 Дана функция y=f(x). Если аргумент меняется от значения х1(хс) до нового значения х2(хн), то разность этих значений х2 - х1(хн-хс) называют приращением аргумента, и обозначают символом ∆х => ∆х= х2 - х1. Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции – приращение ординаты этой точки.
Дана функция y=f(x). Если аргумент меняется от значения х1(хс) до нового значения х2(хн), то разность этих значений х2 - х1(хн-хс) называют приращением аргумента, и обозначают символом ∆х => ∆х= х2 - х1. Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции – приращение ординаты этой точки.
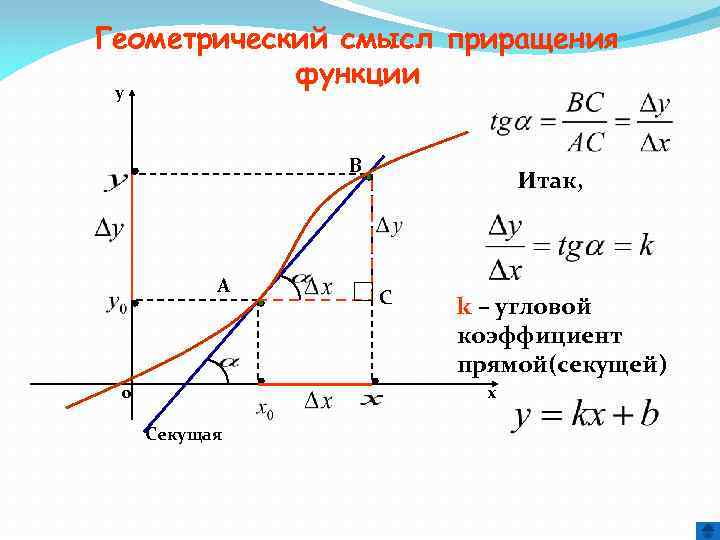 Геометрический смысл приращения функции y B Итак, A С 0 Секущая k – угловой коэффициент прямой(секущей) х
Геометрический смысл приращения функции y B Итак, A С 0 Секущая k – угловой коэффициент прямой(секущей) х
 Пример 1. Найти приращение аргумента и функции y=2 x 2+1, если аргумент x изменяется от 1 до 1, 02. Решение: • Найти приращения аргумента: ∆х=1, 02 -1=0, 02. • Найдем значения функции при старом значении аргумента: yc=2*12+1=3 • Находим значения функции: yн=2*1, 022+1=2*1, 0404+1=3, 0808. Вычитая из нового первоначальное значение функции, найдем приращение функции. ∆y=yн-yс=3, 0808 -3=0, 0808.
Пример 1. Найти приращение аргумента и функции y=2 x 2+1, если аргумент x изменяется от 1 до 1, 02. Решение: • Найти приращения аргумента: ∆х=1, 02 -1=0, 02. • Найдем значения функции при старом значении аргумента: yc=2*12+1=3 • Находим значения функции: yн=2*1, 022+1=2*1, 0404+1=3, 0808. Вычитая из нового первоначальное значение функции, найдем приращение функции. ∆y=yн-yс=3, 0808 -3=0, 0808.
 О великом Ньютоне! Исаак Ньютон (1643 -1727) один из создателей дифференциального исчисления. Главный его труд- «Математические начала натуральной философии» . -оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания. Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
О великом Ньютоне! Исаак Ньютон (1643 -1727) один из создателей дифференциального исчисления. Главный его труд- «Математические начала натуральной философии» . -оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания. Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
 О Лейбнице. Создатель Берлинской академии наук. Основоположник дифференци- ального исчисления, ввёл большую часть современной символики математического анализа. Лейбниц пришёл к понятию производной решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.
О Лейбнице. Создатель Берлинской академии наук. Основоположник дифференци- ального исчисления, ввёл большую часть современной символики математического анализа. Лейбниц пришёл к понятию производной решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.
 Но это не говорит о том, … …что до них эти вопросы не изучались. Задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции. Эпизодически понятие касательной встречалось в работах итальянского математика И. Тартальи. В 17 в. на основе учения Г. Галилея активно развилась кинематическая концепция производной. Понятие производной встречается уже у Р. Декарта, французского математика Роберваля, английского учёного Д. Грегори, в работах И. Барроу. Но систематическое учение с выдвижением двух основных проблем математического анализа развито Ньютоном и Лейбницем.
Но это не говорит о том, … …что до них эти вопросы не изучались. Задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции. Эпизодически понятие касательной встречалось в работах итальянского математика И. Тартальи. В 17 в. на основе учения Г. Галилея активно развилась кинематическая концепция производной. Понятие производной встречается уже у Р. Декарта, французского математика Роберваля, английского учёного Д. Грегори, в работах И. Барроу. Но систематическое учение с выдвижением двух основных проблем математического анализа развито Ньютоном и Лейбницем.
 Последователи учений Ньютона и Лейбница. В последующем развитии идеи анализа (а они очень быстро завоевали популярность и нашли многих последователей), следует в первую очередь назвать имена учеников Лейбница - братьев Бернулли. А. Лопиталь (1661 -1704)который учился у Бернулли, уже в 1696 году издал первый печатный курс дифференциального исчисления. Ряд крупных результатов получил Лагранж, его работы сыграли важную роль в осмыслении основ анализа.
Последователи учений Ньютона и Лейбница. В последующем развитии идеи анализа (а они очень быстро завоевали популярность и нашли многих последователей), следует в первую очередь назвать имена учеников Лейбница - братьев Бернулли. А. Лопиталь (1661 -1704)который учился у Бернулли, уже в 1696 году издал первый печатный курс дифференциального исчисления. Ряд крупных результатов получил Лагранж, его работы сыграли важную роль в осмыслении основ анализа.
 Исаак Ньютон (1643 – 1727) «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад. »
Исаак Ньютон (1643 – 1727) «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад. »
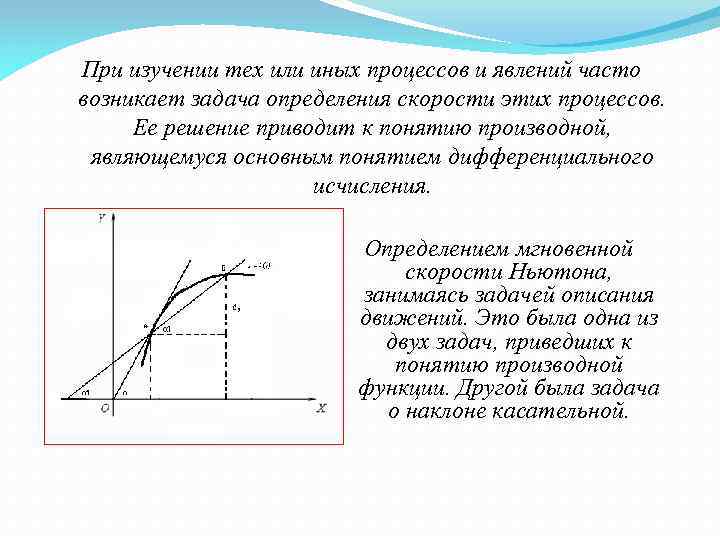 При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления. Определением мгновенной скорости Ньютона, занимаясь задачей описания движений. Это была одна из двух задач, приведших к понятию производной функции. Другой была задача о наклоне касательной.
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления. Определением мгновенной скорости Ньютона, занимаясь задачей описания движений. Это была одна из двух задач, приведших к понятию производной функции. Другой была задача о наклоне касательной.
 S = S(t) – закон неравномерного движения. V мгн = α 1 α ∆x 0 k= tg α =
S = S(t) – закон неравномерного движения. V мгн = α 1 α ∆x 0 k= tg α =
 Свободное падение t t 1
Свободное падение t t 1
 Свободное падение t t 1
Свободное падение t t 1
 Используя слово «предел» , можно сказать, что мгновенная скорость в точке t – это предел средней скорости при стягивании отрезка, на котором она изменяется, в точку t или в символической записи - это скорость
Используя слово «предел» , можно сказать, что мгновенная скорость в точке t – это предел средней скорости при стягивании отрезка, на котором она изменяется, в точку t или в символической записи - это скорость
 .
.
 «Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то эта продолженная таким образом сторона будет называться касательной к кривой. »
«Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то эта продолженная таким образом сторона будет называться касательной к кривой. »
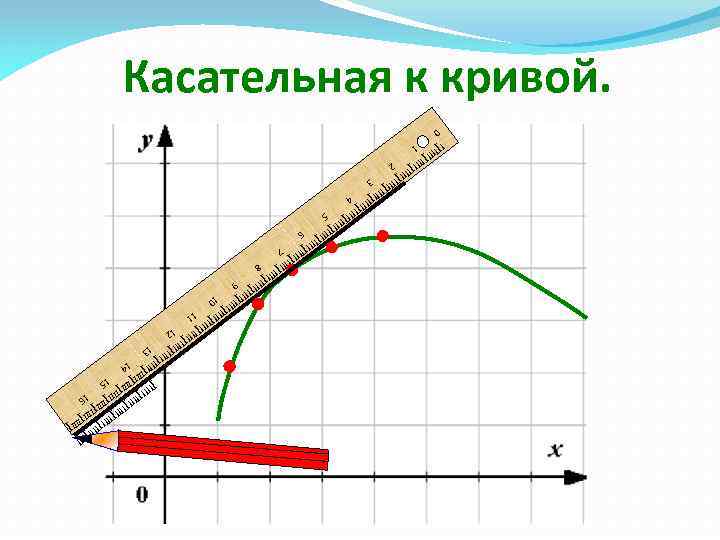 Касательная к кривой. 0 II 1 2 3 4 5 6 II III I 7 II III I 8 9 10 11 12 I III 13 14 I II II IIIIIII IIIIII I IIIII I III II III II IIII III I IIII III I 15 16
Касательная к кривой. 0 II 1 2 3 4 5 6 II III I 7 II III I 8 9 10 11 12 I III 13 14 I II II IIIIIII IIIIII I IIIII I III II III II IIII III I IIII III I 15 16
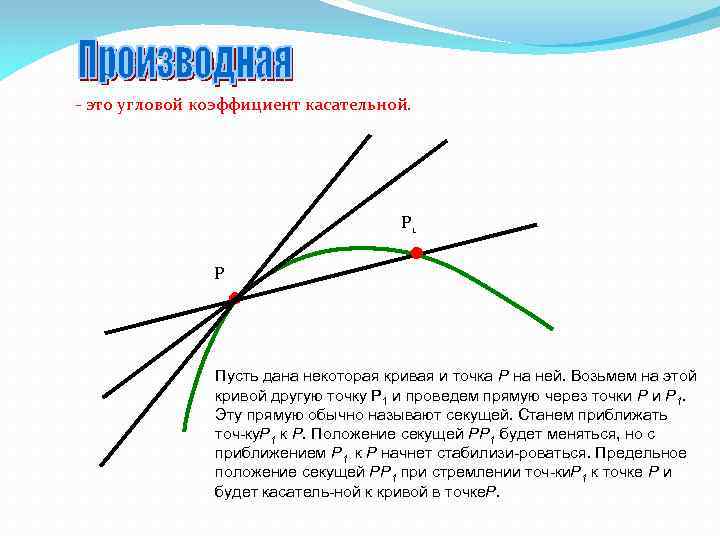 - это угловой коэффициент касательной. Р 1 Р Пусть дана некоторая кривая и точка Р на ней. Возьмем на этой кривой другую точку Р 1 и проведем прямую через точки Р 1. Эту прямую обычно называют секущей. Станем приближать точ ку. Р 1 к Р. Положение секущей РР 1 будет меняться, но с приближением Р 1 к Р начнет стабилизи роваться. Предельное положение секущей РР 1 при стремлении точ ки. Р 1 к точке Р и будет касатель ной к кривой в точке. Р.
- это угловой коэффициент касательной. Р 1 Р Пусть дана некоторая кривая и точка Р на ней. Возьмем на этой кривой другую точку Р 1 и проведем прямую через точки Р 1. Эту прямую обычно называют секущей. Станем приближать точ ку. Р 1 к Р. Положение секущей РР 1 будет меняться, но с приближением Р 1 к Р начнет стабилизи роваться. Предельное положение секущей РР 1 при стремлении точ ки. Р 1 к точке Р и будет касатель ной к кривой в точке. Р.
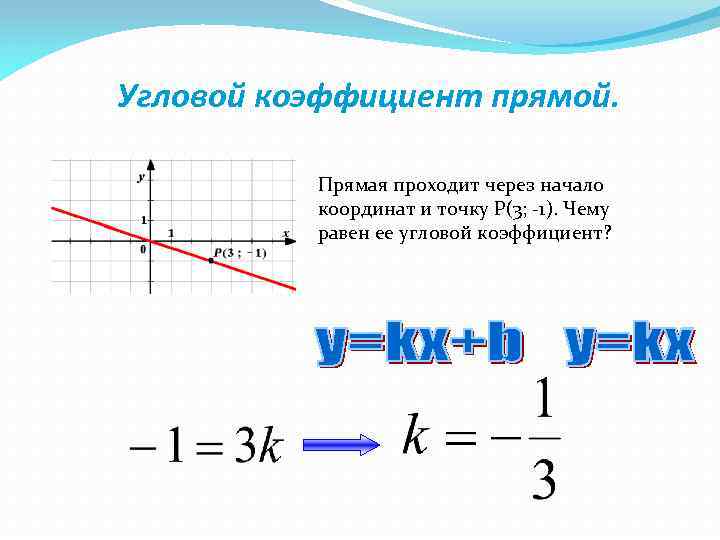 Угловой коэффициент прямой. Прямая проходит через начало координат и точку Р(3; -1). Чему равен ее угловой коэффициент?
Угловой коэффициент прямой. Прямая проходит через начало координат и точку Р(3; -1). Чему равен ее угловой коэффициент?
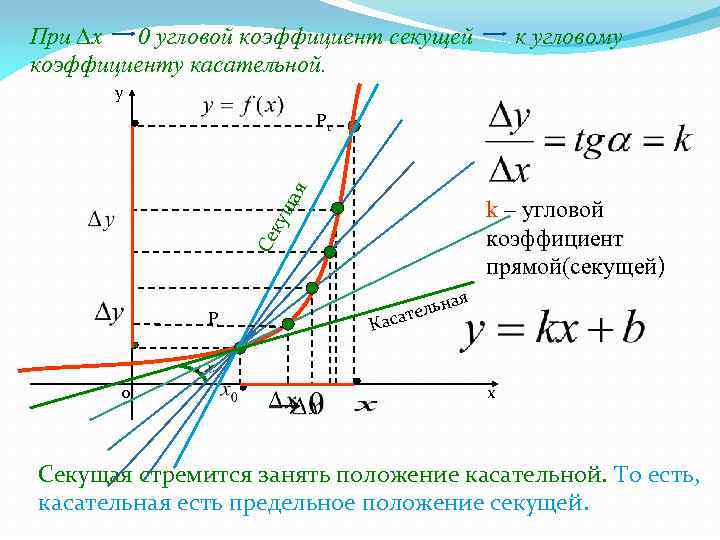 При ∆x 0 угловой коэффициент секущей к угловому коэффициенту касательной. y ща я Р 1 k – угловой коэффициент прямой(секущей) Се ку Р 0 ая ьн ател Кас х Секущая стремится занять положение касательной. То есть, касательная есть предельное положение секущей.
При ∆x 0 угловой коэффициент секущей к угловому коэффициенту касательной. y ща я Р 1 k – угловой коэффициент прямой(секущей) Се ку Р 0 ая ьн ател Кас х Секущая стремится занять положение касательной. То есть, касательная есть предельное положение секущей.
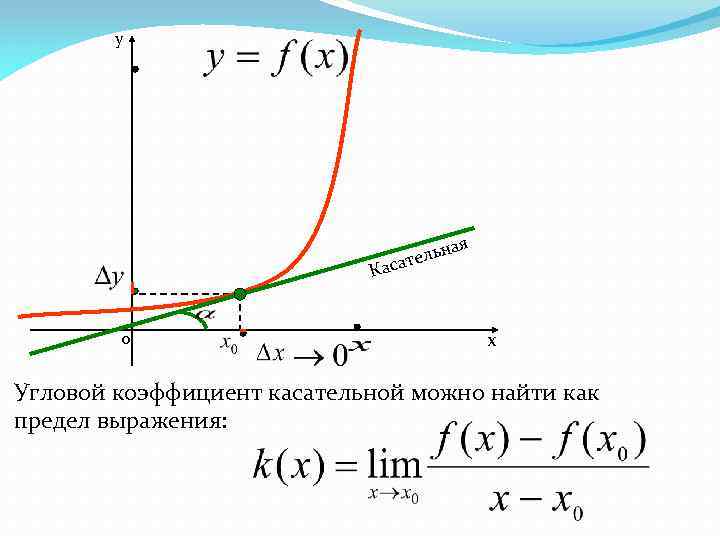 y ая ельн т Каса х 0 Угловой коэффициент касательной можно найти как предел выражения:
y ая ельн т Каса х 0 Угловой коэффициент касательной можно найти как предел выражения:
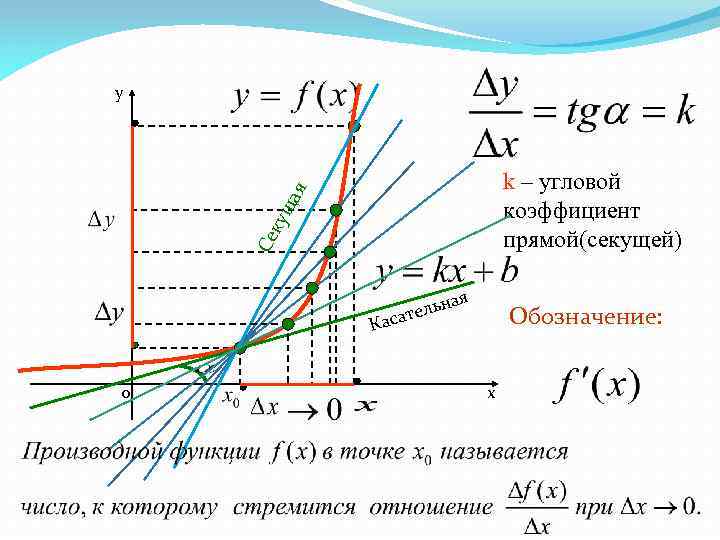 y ща я k – угловой коэффициент прямой(секущей) Се ку ая ьн ател Кас 0 Обозначение: х
y ща я k – угловой коэффициент прямой(секущей) Се ку ая ьн ател Кас 0 Обозначение: х
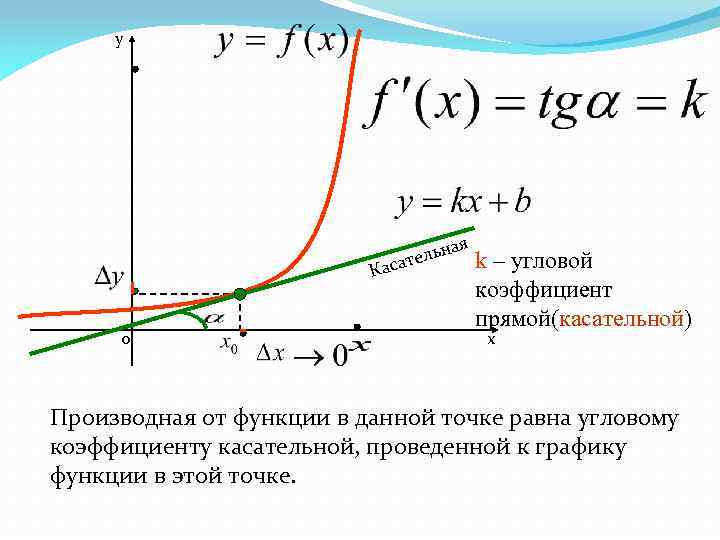 y ая ельн т Каса 0 k – угловой коэффициент прямой(касательной) х Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
y ая ельн т Каса 0 k – угловой коэффициент прямой(касательной) х Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
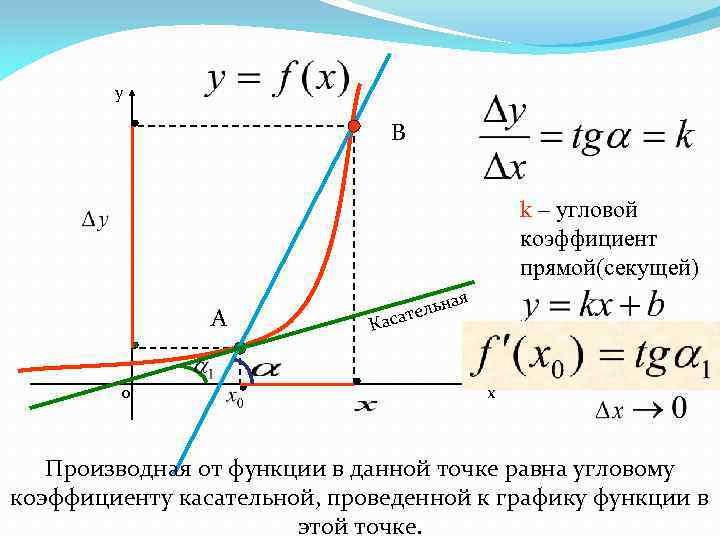 y В k – угловой коэффициент прямой(секущей) А 0 ая ьн ател Кас х Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
y В k – угловой коэффициент прямой(секущей) А 0 ая ьн ател Кас х Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
 Определение. Производной данной функции в точки х называется предел отношения приращения этой функции к приращению аргумента в точке х, когда приращение аргумента стремится к нулю. y’=f’(x)= y=5 x, y’=? 1) ∆y=5(x+∆x)-5 x = 5 x+5∆x-5 x = 5∆x 2) = =5 3) y’= 5=5
Определение. Производной данной функции в точки х называется предел отношения приращения этой функции к приращению аргумента в точке х, когда приращение аргумента стремится к нулю. y’=f’(x)= y=5 x, y’=? 1) ∆y=5(x+∆x)-5 x = 5 x+5∆x-5 x = 5∆x 2) = =5 3) y’= 5=5
 Формула дифференцирования основных элементарных функций.
Формула дифференцирования основных элементарных функций.
 Правило дифференцирования 1) С’=0, C=const Производная постоянной равна нулю. 2) (u+v-w)’= u’+v’-w’ Производная алгебраической суммы конечного числа слагаемых равна алгебраической сумме производных этих слагаемых. 3) (uv)’= u’v + uv’ Производная произведения двух функций равна производной первого сомножителя, умноженной на второй, плюс производная второго сомножителя, умноженная на первый. 4) Производная дроби равна дроби, знаменатель которой равен квадрату знаменателя данной дроби, а числитель равен производной числителя данной дроби, умноженной на ее знаменатель, минус производная знаменателя, умноженная на числитель. 5) (Сu)‘= Сu‘ Постоянный множитель можно вынести за знак производной. 6) Правило дифференцирования сложной функции. Производная функции y по аргументу x равна производной этой функции по промежуточному аргументу u, умноженной на производную промежуточного аргумента и по основному аргументу x (правило цепочки).
Правило дифференцирования 1) С’=0, C=const Производная постоянной равна нулю. 2) (u+v-w)’= u’+v’-w’ Производная алгебраической суммы конечного числа слагаемых равна алгебраической сумме производных этих слагаемых. 3) (uv)’= u’v + uv’ Производная произведения двух функций равна производной первого сомножителя, умноженной на второй, плюс производная второго сомножителя, умноженная на первый. 4) Производная дроби равна дроби, знаменатель которой равен квадрату знаменателя данной дроби, а числитель равен производной числителя данной дроби, умноженной на ее знаменатель, минус производная знаменателя, умноженная на числитель. 5) (Сu)‘= Сu‘ Постоянный множитель можно вынести за знак производной. 6) Правило дифференцирования сложной функции. Производная функции y по аргументу x равна производной этой функции по промежуточному аргументу u, умноженной на производную промежуточного аргумента и по основному аргументу x (правило цепочки).
 Применение производной в исследовании функций • Связь между непрерывностью и дифференцируемостью функции. Если функция f (x) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной. С л е д с т в и е. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке. П р и м е р. Функция y = | x | всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существует касательной к графику этой функции.
Применение производной в исследовании функций • Связь между непрерывностью и дифференцируемостью функции. Если функция f (x) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной. С л е д с т в и е. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке. П р и м е р. Функция y = | x | всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существует касательной к графику этой функции.
 Достаточные признаки монотонности функции. Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале. Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f (x ) убывает на этом интервале. Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак. Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.
Достаточные признаки монотонности функции. Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале. Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f (x ) убывает на этом интервале. Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак. Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

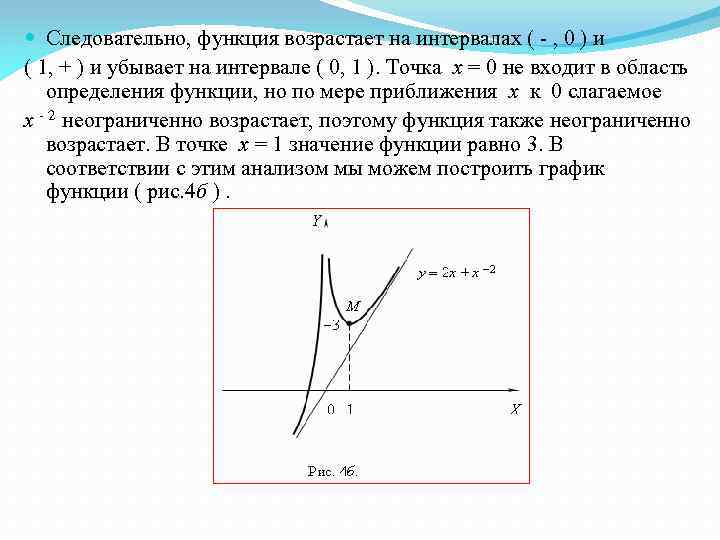 Следовательно, функция возрастает на интервалах ( - , 0 ) и ( 1, + ) и убывает на интервале ( 0, 1 ). Точка x = 0 не входит в область определения функции, но по мере приближения x к 0 слагаемое x - 2 неограниченно возрастает, поэтому функция также неограниченно возрастает. В точке x = 1 значение функции равно 3. В соответствии с этим анализом мы можем построить график функции ( рис. 4 б ).
Следовательно, функция возрастает на интервалах ( - , 0 ) и ( 1, + ) и убывает на интервале ( 0, 1 ). Точка x = 0 не входит в область определения функции, но по мере приближения x к 0 слагаемое x - 2 неограниченно возрастает, поэтому функция также неограниченно возрастает. В точке x = 1 значение функции равно 3. В соответствии с этим анализом мы можем построить график функции ( рис. 4 б ).
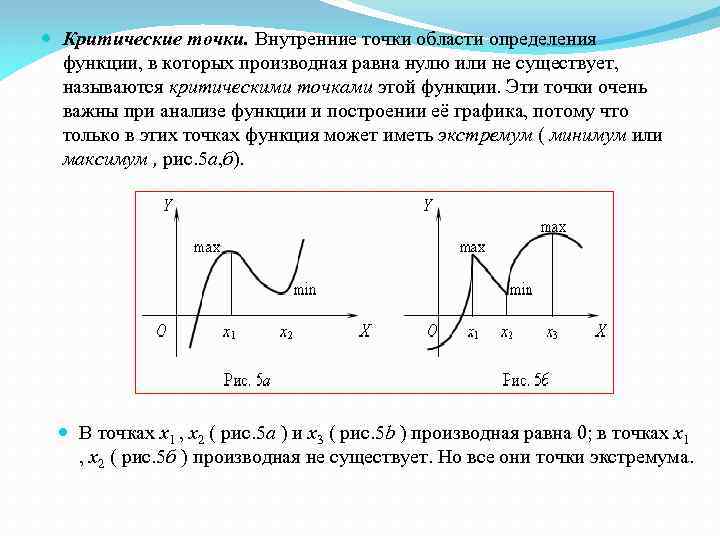 Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум , рис. 5 а, б). В точках x 1 , x 2 ( рис. 5 a ) и x 3 ( рис. 5 b ) производная равна 0; в точках x 1 , x 2 ( рис. 5 б ) производная не существует. Но все они точки экстремума.
Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум , рис. 5 а, б). В точках x 1 , x 2 ( рис. 5 a ) и x 3 ( рис. 5 b ) производная равна 0; в точках x 1 , x 2 ( рис. 5 б ) производная не существует. Но все они точки экстремума.
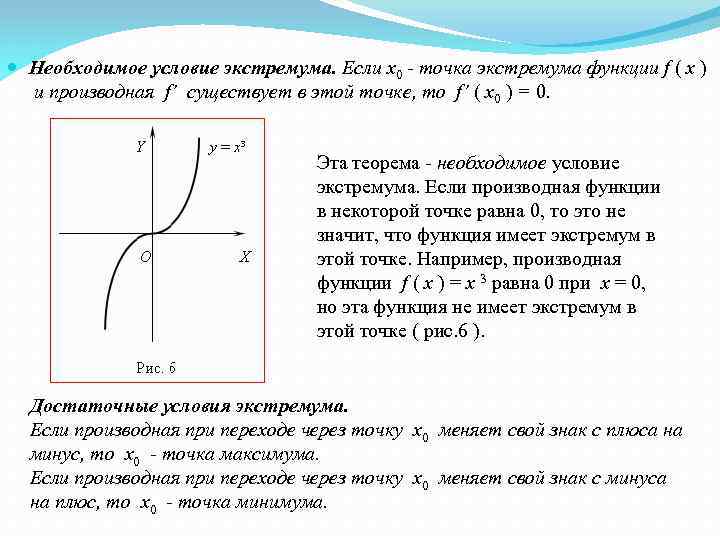 Необходимое условие экстремума. Если x 0 - точка экстремума функции f ( x ) и производная f’ существует в этой точке, то f’ ( x 0 ) = 0. Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке. Например, производная функции f ( x ) = x 3 равна 0 при x = 0, но эта функция не имеет экстремум в этой точке ( рис. 6 ). Достаточные условия экстремума. Если производная при переходе через точку x 0 меняет свой знак с плюса на минус, то x 0 - точка максимума. Если производная при переходе через точку x 0 меняет свой знак с минуса на плюс, то x 0 - точка минимума.
Необходимое условие экстремума. Если x 0 - точка экстремума функции f ( x ) и производная f’ существует в этой точке, то f’ ( x 0 ) = 0. Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке. Например, производная функции f ( x ) = x 3 равна 0 при x = 0, но эта функция не имеет экстремум в этой точке ( рис. 6 ). Достаточные условия экстремума. Если производная при переходе через точку x 0 меняет свой знак с плюса на минус, то x 0 - точка максимума. Если производная при переходе через точку x 0 меняет свой знак с минуса на плюс, то x 0 - точка минимума.
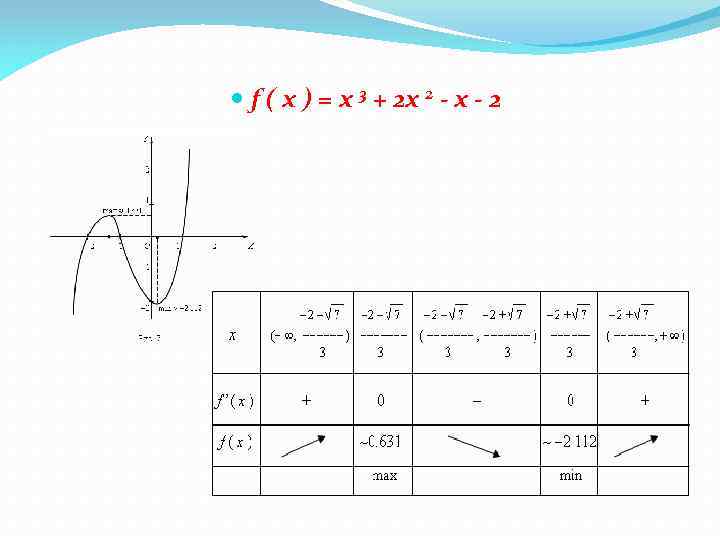 f ( x ) = x 3 + 2 x 2 - x - 2
f ( x ) = x 3 + 2 x 2 - x - 2
 С помощью производных функций, характеризующих физические явления, задаются и другие физические величины. В наше время, в связь с научнотехническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становиться всё более актуальными в решении как простых, так и сверхсложных задач.
С помощью производных функций, характеризующих физические явления, задаются и другие физические величины. В наше время, в связь с научнотехническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становиться всё более актуальными в решении как простых, так и сверхсложных задач.


