Презентация на тему Показательная функция Чалковой Вари Группы

Презентация на тему: Показательная функция Чалковой Вари Группы: СПОЦ 11

Введение показательной функции • Показательная функция — функция обычно обозначаемая ax, где a - некоторое вещественное число, а x — переменная. Если в качестве a (называемого также основанием) стоит число e, то функция называется экспонентой. • Выведем существование и свойства функции • Рассмотрим последовательность , на основе теории пределов. обозначим через Очевидно, что a(0) = 1; a(1) = e по определению; её предел:

• Поэтому если предел существует для какого-то x, то он неотрицателен. Докажем теперь, что при любом x последовательность an(x) сходится и, таким образом, функция a(x) определена для любого вещественного x. Вначале докажем монотонность an(x). Как уже было замечено, при любом x, начиная с некоторого n, все члены последовательности положительны, поэтому безбоязненно рассмотрим при таких n дробь: • Теперь к самому левому множителю применим неравенство Бернулли и получим, что всё выражение больше (строго при n больше некоторого N 1), чем

• • Стало быть, последовательность возрастает. Для существования предела необходима также ограниченность сверху. Докажем и её. an(x)an(-x) = Числитель дроби справа при достаточно больших n больше нуля, но всегда меньше единицы, знаменатель, как только что было доказано, возрастает и при достаточно больших n больше нуля. Зафиксируем какое-нибудь n = N 2, чтобы знаменатель был больше нуля. Тогда левая часть всегда будет меньше , то есть константы. Значит, последовательность действительно ограничена и a(x) определена всюду на R.

Свойства • Опишем свойства введённой нами функции. • 1). a(x+y) = a(x)a(y). Для доказательства этого факта докажем сперва лемму: если • При достаточно больших n |αn| становится меньше единицы; по неравенству Бернулли получаем, что • Видим, что самая левая и самая правая части стремятся к единице, а значит, по теореме о неравенстве пределов, и заключённое между ними выражение стремится к тому же числу, ч. т. д. Теперь доказательство собственно свойства. a(x)a(y) = •

• 2). Из свойства 1 следует, что для любого x a(x) неотрицательна, но a(x) = a(x/2+x/2) = a(x)2, а значит, a(x) всегда положительна. • 3). a(x) возрастает. Действительно, если x 2 > x 1, то a(x 2) = a(x 1 + (x 2 - x 1)) = a(x 1)a(x 2 - x 1), где a(x 1) положительно, а следующий сомножитель больше единицы (так как, по всё тому же неравенству Бернулли, a(x) >= 1+x). • 4). a(x) непрерывна. Докажем непрерывность в нуле: • а значит, предел в нуле равен единице - значению в нуле. Если мы рассмотрим x 0, то увидим, что a(x) = a(x 0)a(x-x 0), при стремлении x к x 0 правый множитель стремится к 1, поэтому предел a(x) в точке равен значению её в этой же точке, ч. т. д. Теперь посмотрим повнимательнее на введённую функцию. a(nx) = a((n - 1)x + x)= = (a(x))n; a(1) = e, a(1/n) = e 1/n, a(m/n) = em/n, a(-m/n) = e-m/n, всё это легко показать. Получилось, что на множестве рациональных чисел введённая функция совпадает с функцией ex; на самом деле, она совпадает с ней на R.

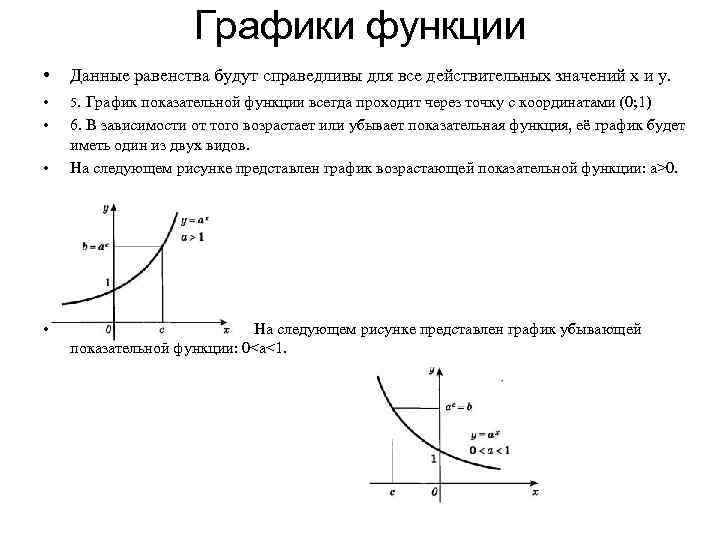Графики функции • • • Данные равенства будут справедливы для все действительных значений х и у. 5. График показательной функции всегда проходит через точку с координатами (0; 1) 6. В зависимости от того возрастает или убывает показательная функция, её график будет иметь один из двух видов. На следующем рисунке представлен график возрастающей показательной функции: a>0. На следующем рисунке представлен график убывающей показательной функции: 0

• И график возрастающей показательной функции и график убывающей показательной функции согласно свойству, описанному в пятом пункте, проходят через точку (0; 1). • 7. Показательная функция не имеет точек экстремума, то есть другими словами, она не имеет точек минимума и максимума функции. Если рассматривать функцию на какомлибо конкретном отрезке, то минимальное и максимальное значения функция будет принимать на концах этого промежутка. • 8. Функция не является четной или нечетной. Показательная функция это функция общего вида. Это видно и из графиков, ни один из них не симметричен ни относительно оси Оу, ни относительно начала координат.