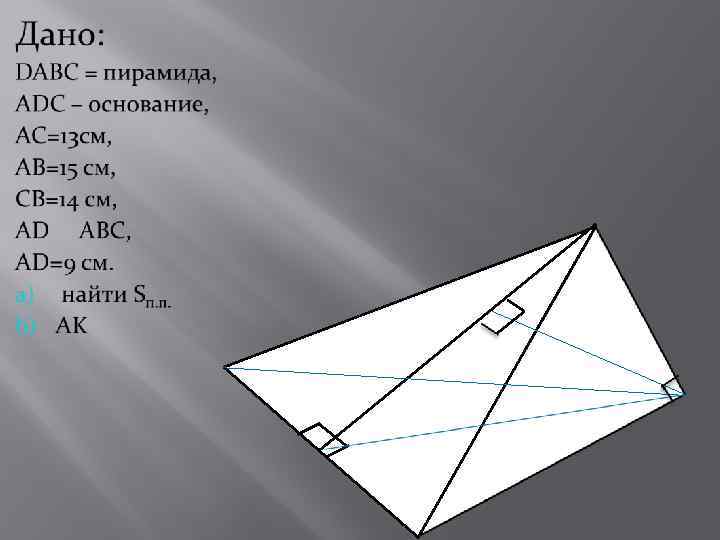
Презентация на тему: Пирамида
Определение Пирами да— многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.
История развития пирамиды в геометрии Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Объем пирамиды был известен древним египтянам. Первым греческим математиком, кто установил, чему равен объём пирамиды, был Демокрит , а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал» , а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.
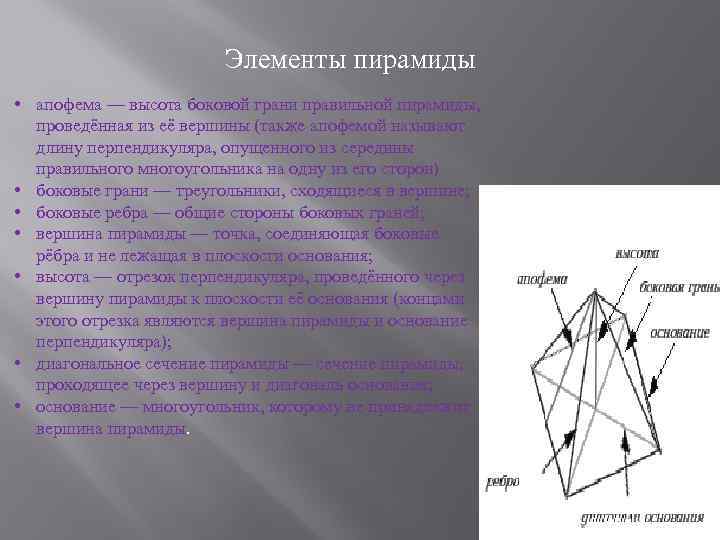Элементы пирамиды • апофема — высота боковой грани правильной пирамиды, проведённая из её вершины (также апофемой называют длину перпендикуляра, опущенного из середины правильного многоугольника на одну из его сторон) • боковые грани — треугольники, сходящиеся в вершине; • боковые ребра — общие стороны боковых граней; • вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания; • высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра); • диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания; • основание — многоугольник, которому не принадлежит вершина пирамиды.
Развёртка пирамиды Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга). Приступая к изучению развёртки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую плёнку. Некоторые из представленных таким образом поверхностей можно путём изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещён с плоскостью без разрывов и склеивания, то такую поверхность называют развёртывающейся, а полученную плоскую фигуру — её развёрткой.
Свойства пирамиды Если все боковые рёбра равны, то: • вокруг основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр; • боковые рёбра образуют с плоскостью основания равные углы; • также верно и обратное, то есть если боковые рёбра образуют с плоскостью основания равные углы, или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые рёбра пирамиды равны. Если боковые грани наклонены к плоскости основания под одним углом, то: • в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр; • высоты боковых граней равны; • площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.
Теоремы, связывающие пирамиду с другими геометрическими телами Сфера • около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу; • в пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
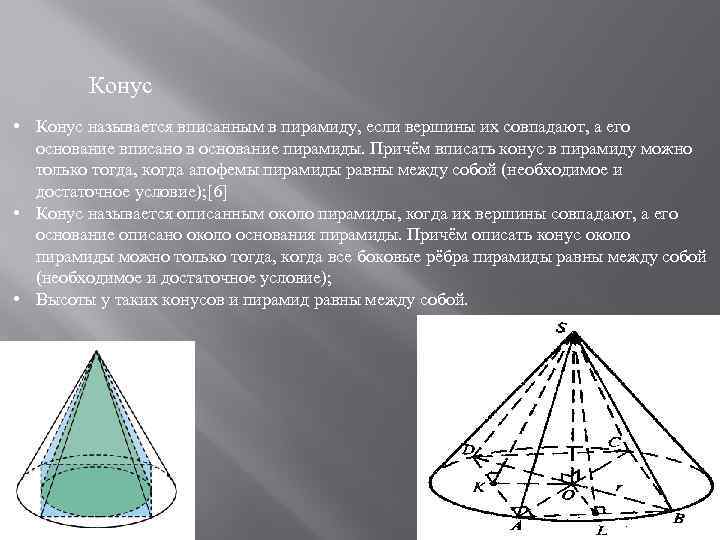Конус • Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие); [6] • Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые рёбра пирамиды равны между собой (необходимое и достаточное условие); • Высоты у таких конусов и пирамид равны между собой.
Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды. Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие).
Особые случаи пирамиды Правильная пирамида Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами: • боковые рёбра правильной пирамиды равны; • в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники; • в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу; • если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна, а каждый из них соответственно, где n — количество сторон многоугольника основания; • площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
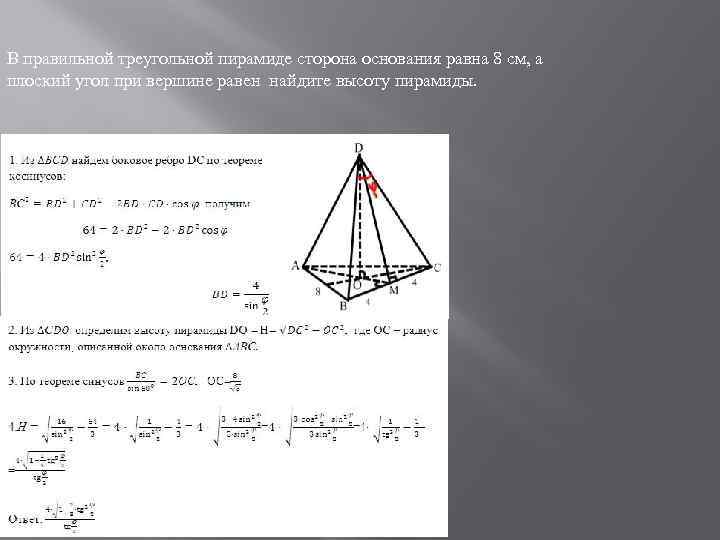В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен найдите высоту пирамиды.
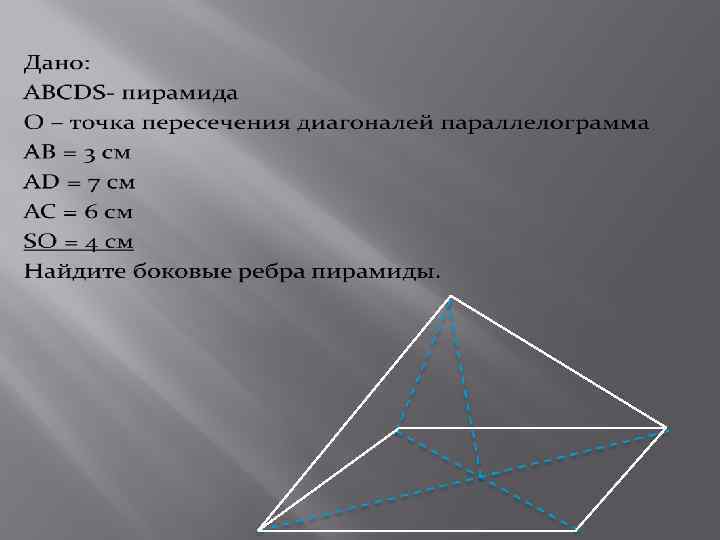
решение
