Презентация на тему: Движение
Презентация на тему: Движение жидкостей и газов. Истечение жидкости из отверстия. Вязкость течение жидкости в трубах. Движение тел в жидкостях и газах. Вихревое движение. Механика жидкостей. Уравнение Бернулли.
Содержание Теория Ø Основные понятия Ø Модель Ø Движение жидкостей и газов Ø Истечение жидкости из отверстия Ø Движение тел в жидкостях и газах Ø Движение тела в вязкой жидкости Ø Подъемная сила Контролирующий тест Пример решения задач
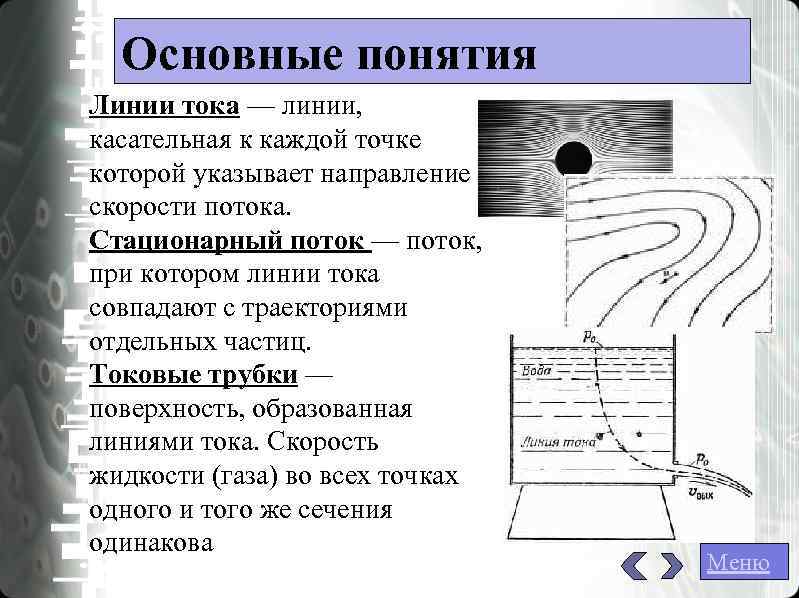
Основные понятия Линии тока — линии, касательная к каждой точке которой указывает направление скорости потока. Стационарный поток — поток, при котором линии тока совпадают с траекториями отдельных частиц. Токовые трубки — поверхность, образованная линиями тока. Скорость жидкости (газа) во всех точках одного и того же сечения одинакова Меню
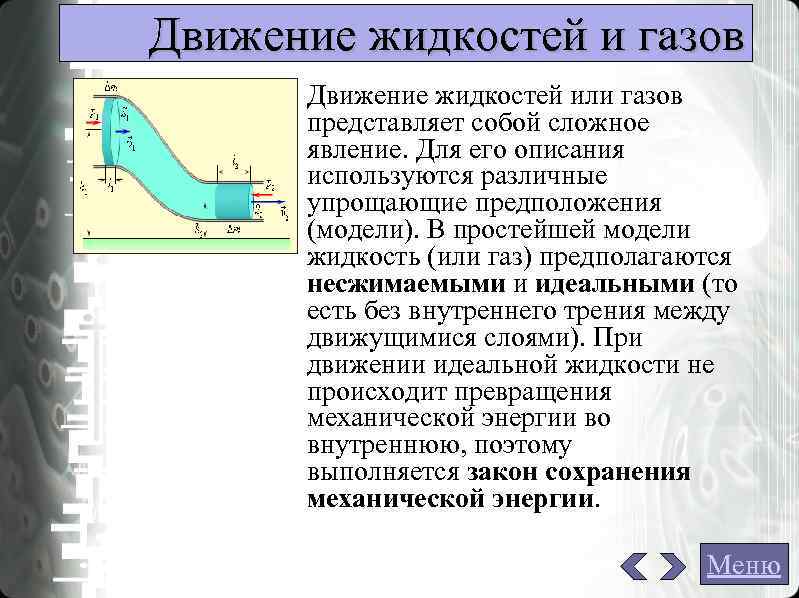
Движение жидкостей и газов Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или газ) предполагаются несжимаемыми и идеальными (то есть без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Меню
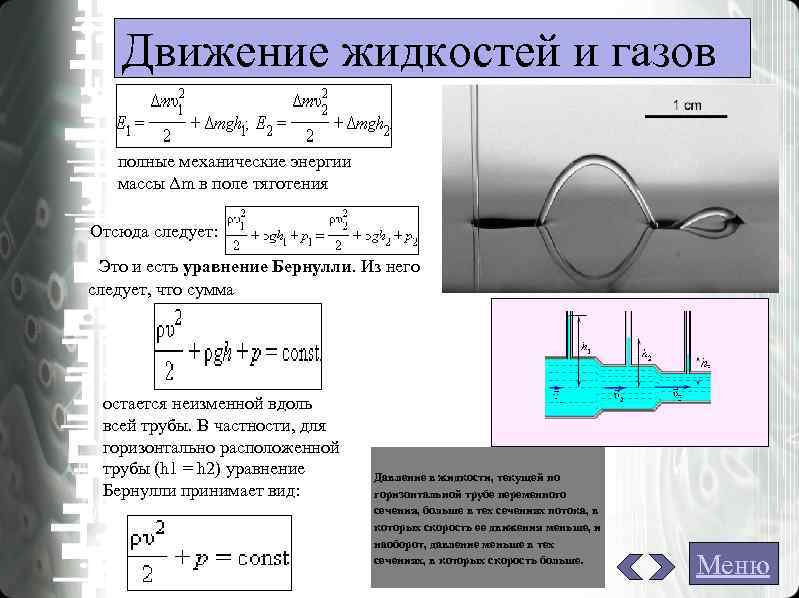
Движение жидкостей и газов полные механические энергии массы Δm в поле тяготения Отсюда следует: Это и есть уравнение Бернулли. Из него следует, что сумма остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы (h 1 = h 2) уравнение Давление в жидкости, текущей по Бернулли принимает вид: горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше. Меню
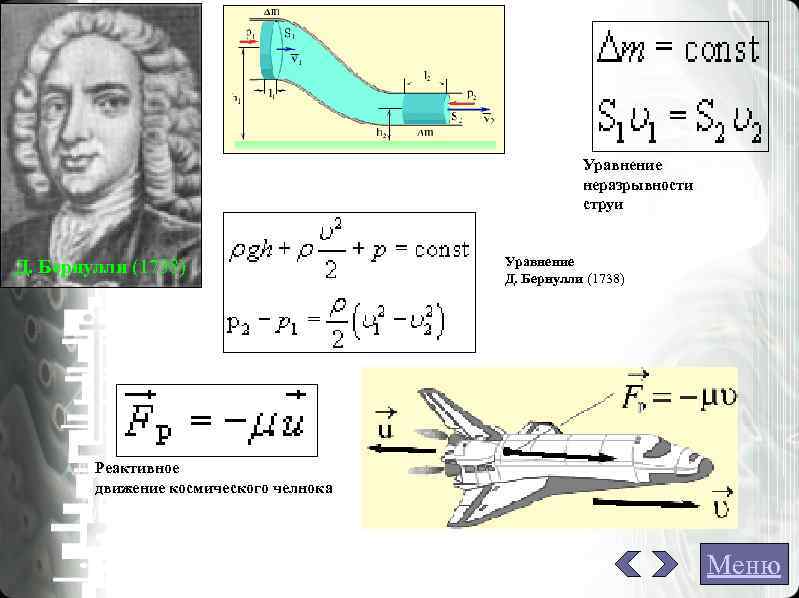
Даниил Бернулли (1700 -1782) Уравнение неразрывности струи Д. Бернулли (1738) Уравнение Д. Бернулли (1738) Реактивное движение космического челнока Меню
Истечение жидкости из отверстия Выделим мысленно в жидко сти трубку тока, сечениями ко торой являются открытая по верхность жидкости S 1 и сече ние струи при выходе из отвер стия S 2 (если не принять спе циальных мер, то сечение струи будет меньше отвер стия). Для всех точек каждого из этих сечений скорость жид кости и высоту h над некото рым исходным v уровнем можно считать одинаковыми. Поэтому к данным сечениям можно применить теорему Бернулли. Давления р1 и р2 в обоих сечениях одинаковы и равны атмосферному. Скоростью v 1 пе ремещения открытой поверх ности жидкости ввиду ее малости можно пренебречь. Поэтому уравнение в данном случае упро щается следующим образом: Формула называется формулой Торричелли. Из нее следует, что скорость истечения жидкости из отверстия, находящегося на глубине h под открытой поверхностью жидкости, совпадет со скоростью, которую приобретает любое тело, падая с высоты h (в случае, если сопротивлением воздуха можно пренебречь). Этот результат получен в пред положении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения, определяемого формулой Торричелли, чем больше внутреннее трение в жидкости. Например, глицерин будет вытекать из сосуда медленнее, чем вода. Меню
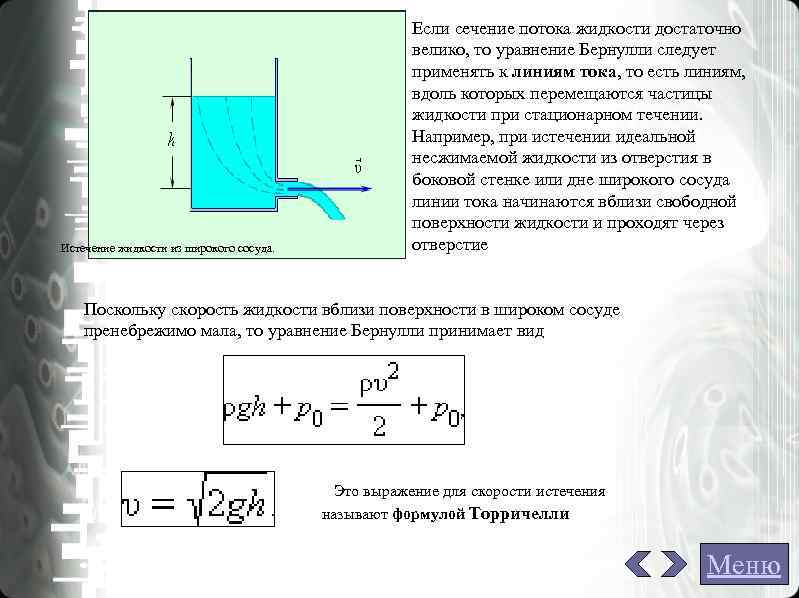
Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока, то есть линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через Истечение жидкости из широкого сосуда. отверстие Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид Это выражение для скорости истечения называют формулой Торричелли Меню
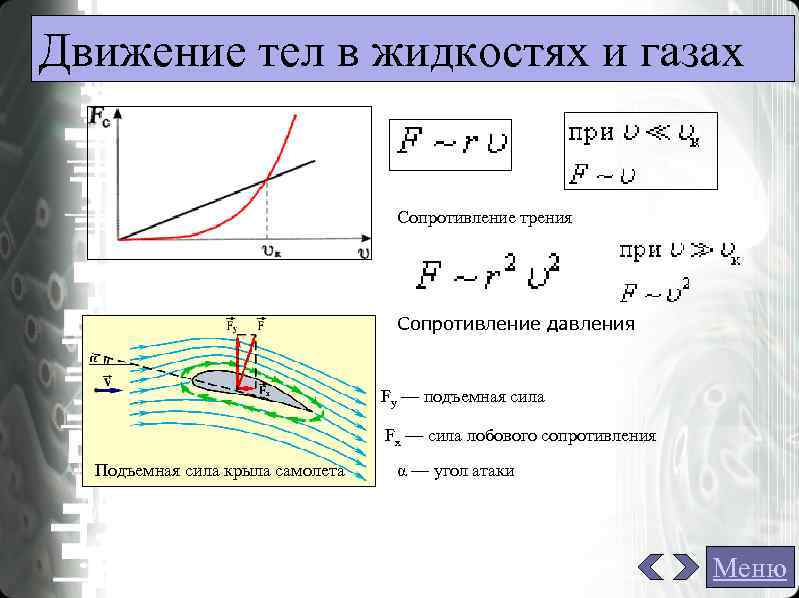
Движение тел в жидкостях и газах Сопротивление трения Сопротивление давления Fy — подъемная сила Fx — сила лобового сопротивления Подъемная сила крыла самолета α — угол атаки Меню
Движение тел в жидкостях и газах. В несжимаемой идеальной жидкости равномерное движение тела произвольной формы должно было бы происходить без лобового сопротивления. Этот результат получил название парадокса Даламбера. Линии тока будут симметричными как отно сительно прямой, проходя щей через точки 2 и 3, так и относительно прямой, проходящей через точки 2 и 4. Теорема Бернулли позволяет по картине линий тока судить о давлении в разных точках потока. Вблизи точек 1 и 3 давление одинаково (и больше, чем в невозмущенном потоке, так как скорость вблизи этих точек меньше). Вблизи точек 2 и 4 давление также одинаково (и меньше, чем в невозмущенном потоке, так как скорость вблизи этих точек, больше) Следовательно, результирующая сил давления на по верхность цилиндра (которая в отсутствие вязкости могла бы обусловить лобовое сопротивление) будет равна нулю. Здесь показаны линии тока при обтекании идеальной жидкостью полуцилиндра. Вследствие идеального обтекания линии тока несимметричны относитель но прямой, проходящей через точки 2 и 4. Однако от носительной прямой, проходящей через точки, 1 и 3 картина линий тока несимметрична. Вблизи точки 2 где линии гуще, давление меньше, чем вблизи дочки 4 , в результате чего возникает подъемная сила. Меню
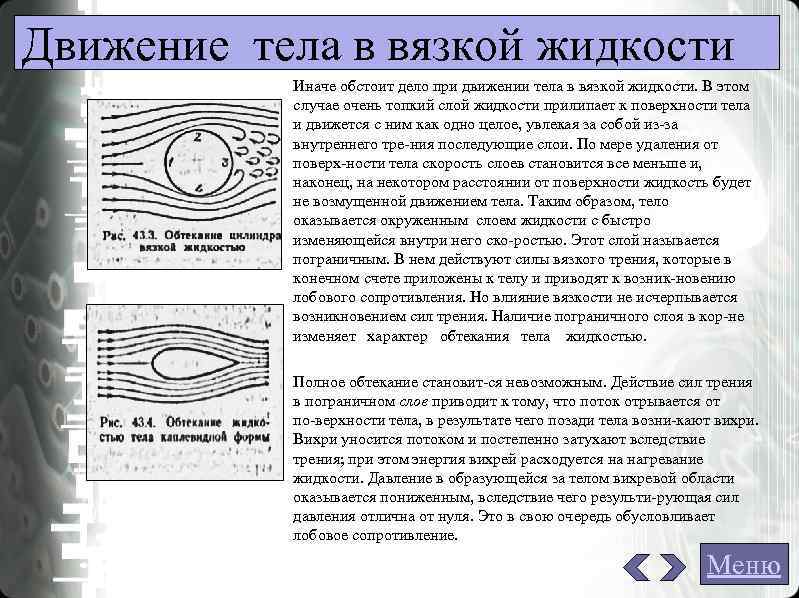
Движение тела в вязкой жидкости Иначе обстоит дело при движении тела в вязкой жидкости. В этом случае очень топкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из за внутреннего тре ния последующие слои. По мере удаления от поверх ности тела скорость слоев становится все меньше и, наконец, на некотором расстоянии от поверхности жидкость будет не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости с быстро изменяющейся внутри него ско ростью. Этот слой называется пограничным. В нем действуют силы вязкого трения, которые в конечном счете приложены к телу и приводят к возник новению лобового сопротивления. Но влияние вязкости не исчерпывается возникновением сил трения. Наличие пограничного слоя в кор не изменяет характер обтекания тела жидкостью. Полное обтекание становит ся невозможным. Действие сил трения в пограничном слое приводит к тому, что поток отрывается от по верхности тела, в результате чего позади тела возни кают вихри. Вихри уносится потоком и постепенно затухают вследствие трения; при этом энергия вихрей расходуется на нагревание жидкости. Давление в образующейся за телом вихревой области оказывается пониженным, вследствие чего результи рующая сил давления отлична от нуля. Это в свою очередь обусловливает лобовое сопротивление. Меню
Подъёмная сила Самолет поддерживается в воздухе подъемной си лой, действующей на его крылья. Лобовое сопротивление играет при полете самолета вредную роль Поэтому крыльям и фюзеляжу самолета придают удобообтекаемую форму. Вследствие асим метричной формы и наклонного расположения крыла скорость воздуха над крылом оказывается больше (а, следовательно, давление меньше), чем под крылом. Благодаря этому создается подъем ная сила. Существенную роль в образовании подъ емной силы играет вяз кость воздуха, которая обусловливает образова ние вихрей, отрывающих ся от задней кромки крыла Теория подъемной силы крыла самолета была создана Н. Е. Жуковским. Он показал, что существенную роль при обтекании крыла играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение (циркуляция) воздуха вокруг крыла. В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего потока, в нижней части эти скорости направлены в противоположные стороны. Это и приводит к возникновению разности давлений и появлению подъемной силы. Циркуляция воздуха, обусловленная силами вязкого трения, возникает и вокруг вращающегося тела (например, цилиндра). При вращении цилиндр увлекает прилегающие слои воздуха, вызывая его циркуляцию. Если такой цилиндр установить в набегающем потоке воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса. иллюстрирует обтекание вращающегося цилиндра набегающим потоком. Эффект Магнуса проявляется, например, при полете закрученного мяча при Меню игре в теннис или футбол.
Контролирующий тест 1 Уравнение Бернулли Формула Торричелли Уравнение Рейнольдса Меню
Контролирующий тест При движении идеальной жидкости не происходит превращения 2 механической энергии во внутреннюю, поэтому выполняется: Закон сохранения механической энергии Парадокс Даламбера Эффект Магнуса
Контролирующий тест 3 Теория подъемной силы крыла самолета была создана … Жуковским Стоксом Торричелли Меню
Контролирующий тест 4 Линия, касательная к которой в каждой точке направлена по вектору вихря; совокупность вихревых линий, проходящих через замкнутую кривую, образует вихревую трубку : Вихревая линия Линия тока Ламинарное течение
Контролирующий тест Совокупность векторов v(t), заданных для 5 всех точек пространства, называется : Ламинарным течением Полем вектора скорости Движением в сужающейся трубке Меню
Контролирующий тест 6 для не сжимаемой жидкости при стационарном течении про изведение v в любом сечении данной трубки тока S имеет одинаковое значение: Теорема о неразрывности струи Теорема Бернулли Теория Рейнольдса
Контролирующий тест 7 Формула Пуазейля Формула Торричелли Уравнение Бернулли Меню
Пример решения задач: Меню
Верно
Неверно
Верно
Неверно
Верно
Неверно
Верно
Неверно
Верно
Неверно
Верно
Неверно
Верно
Неверно