Презентация log fun

«Истинное знание состоит не в знакомстве с фактами, которое делает человека лишь педантом, а в использовании фактов, которое делает его философом» . Г. Бокль

Логарифмическая функция Урок — подготовки к ЕГЭ МОУ «Могочинская СОШ» Томская обл учитель математики высшей категории Тарасенко Ирина Валериевна

Цель обобщение и систематизация теоретического материала по данной теме; • отработка умений и навыков применения формул для преобразования логарифмических выражений и решения уравнений и неравенств; • развитие навыков работы с дополнительной литературой, с историческим материалом; • воспитание эстетических качеств и умения общаться

Задачи Повторить формулы, относящиеся к теме «Логарифмическая функция» ; Закрепить умения преобразовывать логарифмические выражения и решать логарифмические уравнения и неравенства Формирование интереса к изучению математики Подготовка к ЕГЭ

Содержание Разминка. «Лови ошибку!» – вспомним теорию Гонка с препятствиями. «Логарифмический дартс» Гонка по пересеченной местности. «Испытание графиками» Переменка. Логарифмическая «комедия 2 >3>3 » . Практичность теории. Проба сил. «Логарифмы в жизни и быту» — творческое домашнее задание

Лови ошибку! Понятия Формулы 1. Определение логарифма числа по заданному основанию 2. Основное логарифмическое тождество. 3. Формула логарифм произведения. 4. Формула логарифм частного. 5. Формула логарифм степени. 6. Формула логарифмического перехода от одного основания к другому основанию. 7. Логарифм, значение которого равно единице 8. Логарифм, значение которого равно нулю 9. Запись числа через логарифм 21 2 1 logloglogxx x x 0, 1, 0, logbaaabxbx a 01 log a 1 loglogab ba ca ca log 2121 logloglogxxxx a bb b a c calog 1 log; loglog bnba n aloglog ca c alog

Проверь себя! Понятия Формулы 1. Определение логарифма числа по заданному основанию 2. Основное логарифмическое тождество. 3. Формула логарифм произведения. 4. Формула логарифм частного. 5. Формула логарифм степени. 6. Формула логарифмического перехода от одного основания к другому основанию. 7. Логарифм, значение которого равно единице 8. Логарифм, значение которого равно нулю 9. Запись числа через логарифм 21 2 1 logloglogxx x x 0, 1, 0, logbaaabxbx a 01 logaa ca ca log 2121 logloglogxxxx a b b b a c c alog 1 log; log log bnba n aloglog ca c alog

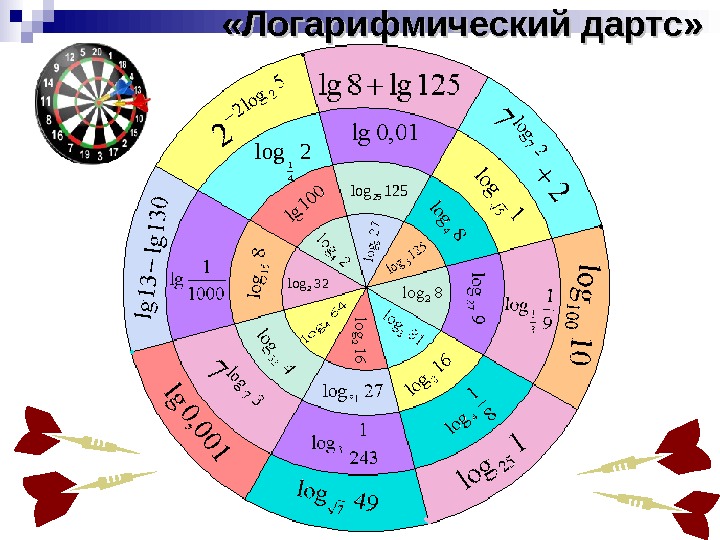
«Логарифмический дартс» 125 log 252 log 41 32 log

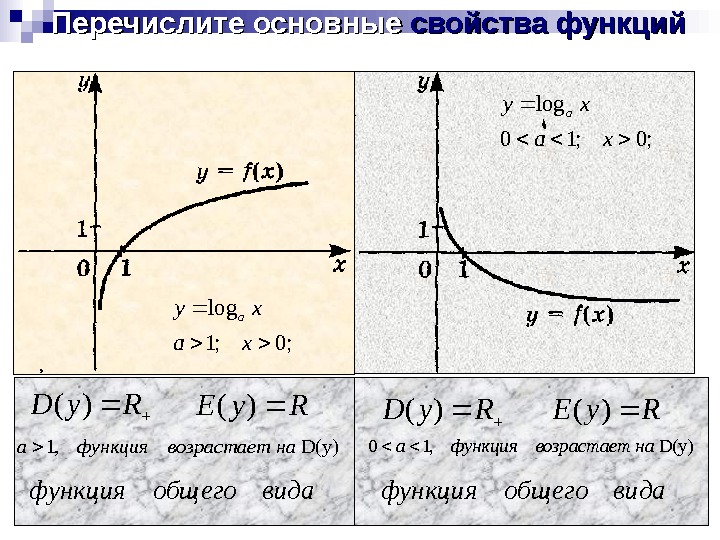
Перечислите основные свойства функций Ry. D )( D(y), 1 навозрастаетфункцияa Ry. E )( видаобщегофункция. Ry. D)( Ry. E )( D(y), 10 навозрастаетфункцияa видаобщегофункция ; 0; 1 log xa xya Ry. D)( ; 0; 10 log xa xy a

Найти область определения функции 5, 1 23 32 32 023 xx x 5, 1 ]5, 1; ()4 ); ; 5, 1()3 ); 5, 1; ()2 ); 5, 1; ()1 )23(log 5, 0 xy

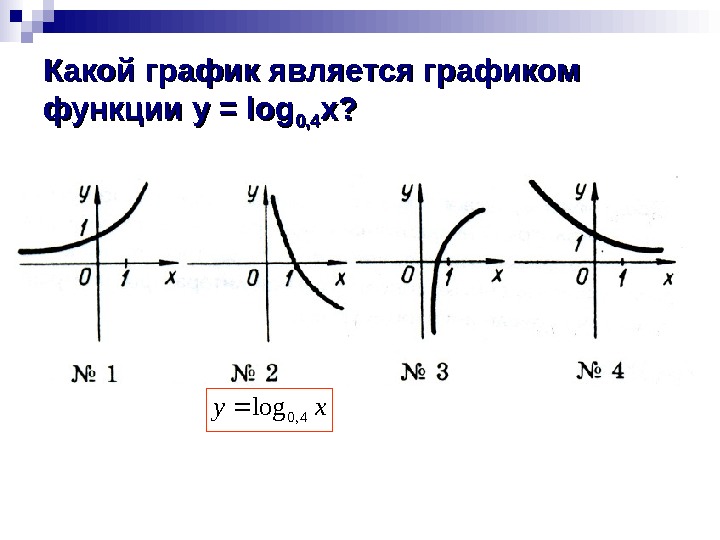
Какой график является графиком функции y = log 0, 4 xx ? ? xy 4, 0 log

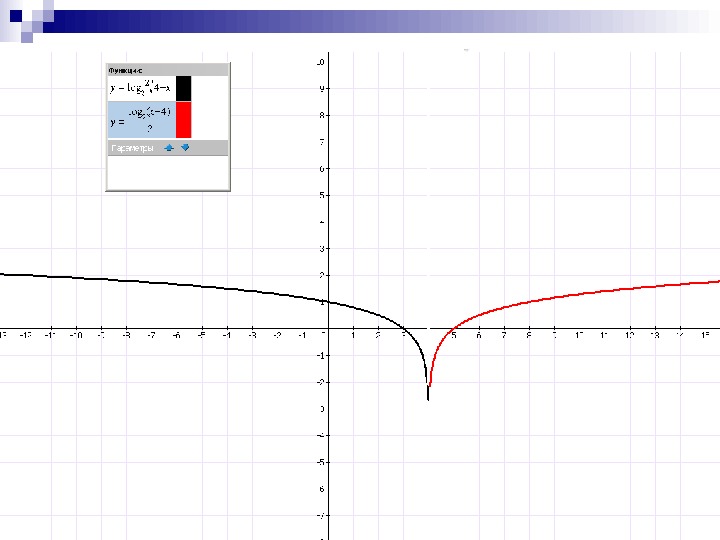
Совпадают ли графики функций? Постройте графики данных функций. 2 )4(log y 4 log 2 2 x иxy 4 04 )4(log 5, 02 x x xy x 5 8 12 5, 25 5, 125 y 0 1 1, 5 -1 -1, 5 4 04 )4(log 5, 0 y 2 x x xx -12 — 4 2 0 3 3, 5 3, 25 y 2 1, 5 0, 5 1 0 -0, 5 —

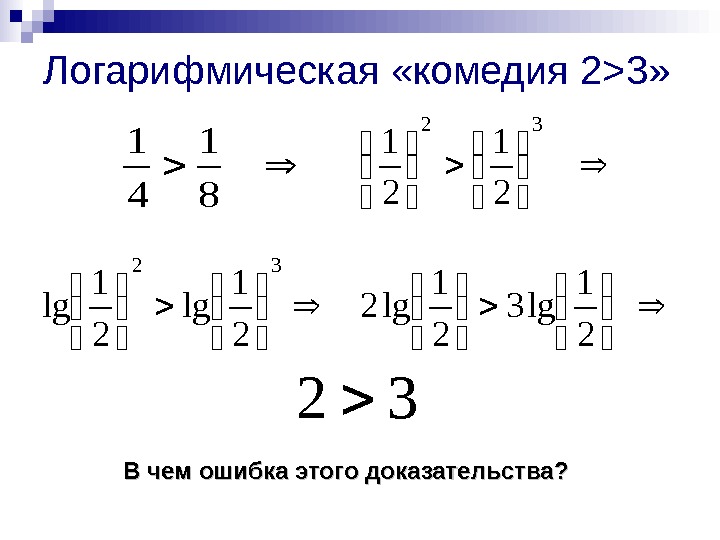
Логарифмическая «комедия 2 > 3» 8 1 4 1 32 21 21 32 21 lg 3 21 lg 2 32 В чем ошибка этого доказательства?

Логарифмическая «комедия 2 >3 » Решение: 0 2 1 lg 21 lg 3 21 lg

Уравнения Методы решения. Определить метод решения уравненийbxf a)(log cxfxf aa )(log 2 )()( 3)( 1 2 xfxf xf )(log )()( xfxf xbxa )(log xgxf aa )(log xfxf ba ba cxgxf aa)(log По определению логарифма Метод потенциирования Метод приведения к одному основанию Метод подстановки Метод логарифмирования Использование основного логарифмического тождества Сворачивание в один логарифм

Итог «Математической гонки» « 5» — свыше 32 баллов « 4» — 26 – 32 баллов « 3» — 15 – 25 баллов

Решите уравнение 1) 3, 25 2) 4 3) 1 4) 1, 25 Решите неравенство 1) (- ; -2) 2) (- ; -2] 3) (-2; + ) 4) [-2; + ) Укажите промежуток, которому принадлежит корень уравнения: 1) (4 ; 5 ) 2) (7; 10) 3) ( 20; 25) 4) (11; 13) Упростите выражение 1) 4 2) 3) 4) 9 Проба сил 1, 5 log 1 2 х 0, 5 log 1 0, 5 1 х . . 9 log 15 log 2255 7 log 2 9 15 log 225 3 10 log 25. 2 log 23 log 66 x 1 A 2 A 3 A 4 A Ответы: 1 2 3 4 Баллы

Логарифмы в жизни и быту История возникновения логарифмов Логарифмические диковинки Логарифмы в музыке Логарифмы в астрономии Логарифмическая спираль Логарифмы и экономика Логарифмы и психология Логарифмы в литературе