Презентация лекция ТА 2с 2 продолж -6

Описание и преобразование управляющих процессов. Сети Петри и их модификация.

Основная задача начального этапа проектирования УА – выбор формализованного языка. Основные понятия – базис сетей Петри: 1. событие; 2. условие. Сеть Петри – структура УП ↓ это последовательность процедур Условия → событие Состояние системы – это множество условий Событие → новые условия → → изменение состояния системы События – множество переходов T={t 0 , t 1 , …, tr } Условия – множество позиций A={a 0 , a 1 , …, af } I – входная функция связь T и A O – выходная функция I – отображает t v (v=0 r) в мн-во позиций I(t v ) – входные позиции перехода O – отображает t v в мн-во позиций O(t v ) – выходные позиции перехода a µ — входная позиция tv , если aµ ϵ I(tv ) a µ — выходная позиция tv , если aµ ϵ O(tv ) Сеть Петри – N = (A, T, I, O)

Пример: A = {a 0 , a 1 , a 2 , a 3 , a 4 } T = {t 0 , t 1 , t 2 , t 3 , t 4 } I(t 0 ) = a 0 I(t 1 ) = a 1 I(t 2 ) = a 2 I(t 3 ) = a 3 I(t 4 ) = a 4 O(t 0 ) = a 1 O(t 1 ) = a 2 O(t 2 ) = a 3 O(t 3 ) = a 4 I – матрица следования O – матрица предшествования Графическое представление сети Петри Типы вершин: 1. позиции – « O » 2. переходы – «–» if (a µ — вход для t v ) , then ( дуга a µ → t v ) if (a µ — выход для t v ) , then ( дуга t v → a µ ) ↓ G = (V, W) – ориентированный двудольный мультиграф, где V – множество вершин W – множество направленных дуг V = A U T A ∩ T = Ø позиция – условие ↓ Выполнение условия – маркировка позиции (метка – «точка» в позиции) ↓ ʘ ↓ Если несколько точек – то « емкость условия »

f -вектор маркировки сети Петри. N = (A, T, I, O, M 0 ) , где M 0 – вектор начальной маркировки Пример: M 0 = (1, 0, 0) Разрешающие метки реализация активного перехода ↓ замена маркировки сети M на M’ ( непосредственно достижимая из M ) Достоинства языка сети Петри: 1. позволяет описывать параллельные процессы; 2. имеет средства для задания конфликтных состояний. q ω > q Выполнение сети → связанные последовательности: 1. реализуемых переходов 2. маркировок M 0 , M 1 , M 2 , …распределение меток в позициях ↓ порядок выполнения сети ↑ — зависит от последовательности реализации переходов ______________________________________ переход реализуется если он активен, т. е. число меток во вх. позиц. = > числу дуг, соединяющих ее с эти переходом

Безопасная сеть Петри. 1. запрещено наличие кратных дуг между позициями и переходами; 2. вектор маркировки может содержать лишь 0 и 1; 3. реализация активного перехода возможна, если ни 1 из его выходных позиций не содержит меток – число меток в любой позиции не больше 1; 4. конечное число состояний – 2 f при f позициях. Ограниченная сеть Петри. k → k- безопасная позиция или k -ограниченная k’ >= k – k’ -безопасной kmax Ограничение оригинальной сети Петри – моделирование примитивных событий. ________________ это сеть позиция-переход ↓ автоматная сеть ↓ маркированный граф ________________ сети с предикатами на переходах ↓ расширение ее описательных возможностей ________________ Введение позиции времени в сети Петри. 1. Временные сети : переход – t ; 2. Тайм-аутные сети : переход – a и b.

Тайм-аутные сети Петри. 0<=a<=b q (q+a) (q+b) Помеченные сети Петри. метка – цвет 1 позиция – несколько цветов Численные сети Петри. 1. метки любой природы и величины; 2. условия активизация и результата реализации независимы; 3. при реализации переходов изменяется маркировка входных и выходных позиций и содержимое памяти данных Использование дуг разных типов в сети Петри. Существуют: 1. Простые дуги: 1. 1. активизирующая ; 1. 2. сдерживающая ; 1. 3. входная ; 1. 4. выходная ; 2. Составные дуги : 2. 1. активизирующая входная ; 2. 2. сдерживающая выходная.

Управляющие процессы и их формализованное описание.

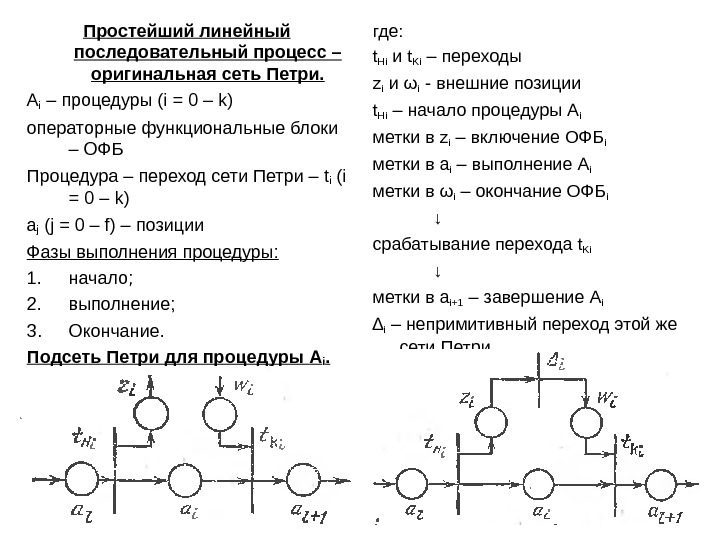
Простейший линейный последовательный процесс – оригинальная сеть Петри. Ai – процедуры ( i = 0 – k) операторные функциональные блоки – ОФБ Процедура – переход сети Петри – t i (i = 0 – k) a j (j = 0 – f) – позиции Фазы выполнения процедуры: 1. начало; 2. выполнение; 3. Окончание. Подсеть Петри для процедуры A i. где: t Hi и t Ki – переходы z i и ω i — внешние позиции t Hi – начало процедуры A i метки в z i – включение ОФБ i метки в a i – выполнение A i метки в ω i – окончание ОФБ i ↓ срабатывание перехода t Ki ↓ метки в a i+1 – завершение A i ∆ i – непримитивный переход этой же сети Петри

Если выполнение процедуры – неделимое событие, то: фрагмент с t. Hi , t. Ki , ∆i и zi , ai , ωi – на tiд C i (i = 0 – l) – разделяемые ресурсы q – число экземпляров i -го ФР ↓ q – кратность ресурса C i – C i q ↓ его могут использовать α <= q процедур при q=1 — у ресурса 2 состояния q+1 внутренние или собственные ресурсы Процедуры A i линейного процесса: 1. {C в i } – множество ФР – уже владеет; 2. {C з i } – множество ФР – запрашивает; 3. {C о i } – множество ФР – освобождает. Это длительный переход. У него есть время выполнения. Функциональные ресурсы (ФР) Собственный ФР Разделяемый ФР Пример: Процесс из 5-и последовательно выполняемых процедур A i при следующем распределении 3-х ФР C j : A 1 ({C 2 }, {-}); A 2 ({C 2 }, {C 1 }, {C 2 }); A 3 ({C 1 }, {C 3 }, {C 1 , C 3 }); A 4 ({-}, {C 2 , C 3 }, {C 3 }). С j – ресурсные внутренние позиции T д i — длительные переходы a µ — основные внутренние позиции

Пример: Если для Ai – {Cвi }=C 1 , {Cзi }=C 3 , C 4 и {Cоi }=C 1 , C 4 , то A i ({C 1 }, {C 3 , C 4 }, {C 1 , C 4 }) {C зi }∩{Cвi }=Ø Иногда: {C вi }=Ø и {Cзi }={Cоi } Особенности описания параллельного линейного процесса в сети Петри. 1. длительные переходы – процедуры; 2. t R – переходы распараллеливания; 3. t S – переходы соединения; 4. наличие элементарных подпроцессов; 5. c обственные ФР подпроцесса Пример:

Пример: Особенности описания разветвленного процесса в сети Петри. 1. позиции альтернативного разветвления; 2. позиции альтернативного соединения; 3. набор значений логических условий в конфликтных переходах альтернативного разветвления;

Логические ресурсы системы – ЛР. D i (i = 1 – m) – ЛР в ЛР D s проверяется p s – условие Внутренние ЛР A i ( {P 1 i }, {P 2 i } ) Пример: A i ( {p 1 , p 2 }, {p 2 , p 3 } ) p s – {P 2 i } – изменяется A i → D s – занято p s – {P 1 i } – не изменяется A i → D s – не занято Описание ЛР в сети Петри. d s – наличие метки – нет монополии D s d s 1 – наличие метки – p s = 1 d s 0 – наличие метки – p s = 0 Пример 1 : A i зависит от ЛУ ( p s ϵ D s ) и изменяет его (p s ) A i ( {p s , p s } ) и A j ( {p s , p s } ) входные позиции для t д i (t д j ) : a µ , d s и d s 1 (d s и d s 0 ) выходные позиции для t д i (t д j ) : a µ +1 ( a µ+2 ) , d s и d s 0 (d s и d s 1 )

Пример 2: A i не зависит от p s , но меняет его. входные позиции t д i : a µ , d s Т. к. p s не проверяется в начале, то: 1. удаляется метка из d s 0 ( или d s 1 ) 2. помещается метка в d s 0 ( или d s 1 ) если после A i p s = 0 ( или 1) Пример 3: A i зависит от p s , но не меняет его. ↓ новый тип дуг – неизменяющиеся. t v c a µ неизменяющейся дугой, то в a µ должна быть метка, но она не удаляется Если A i ( {p s }, {-} ) , то d s 1 c t д i неизменяющейся дугой Если A i ( {p s }, {-} ) , то d s 0 c t д j неизменяющейся дугой d s не используется

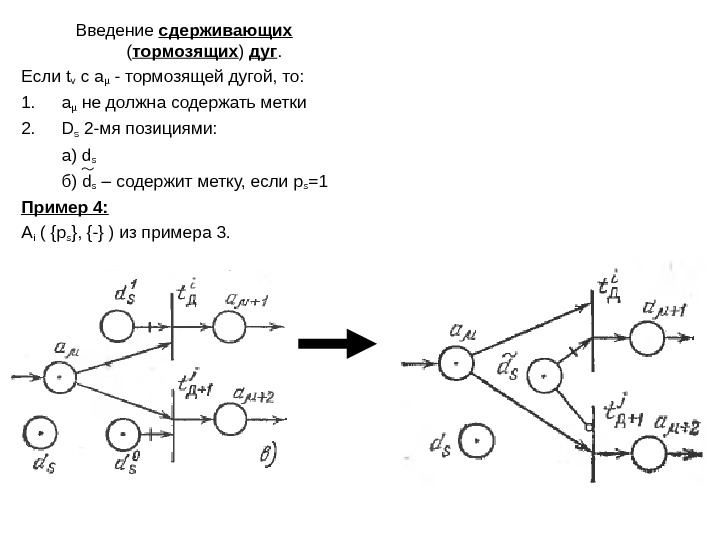
Введение сдерживающих ( тормозящих ) дуг. Если t v c a µ — тормозящей дугой, то: 1. a µ не должна содержать метки 2. D s 2-мя позициями: а) d s б ) d s – содержит метку, если p s =1 Пример 4: A i ( {p s }, {-} ) из примера 3.

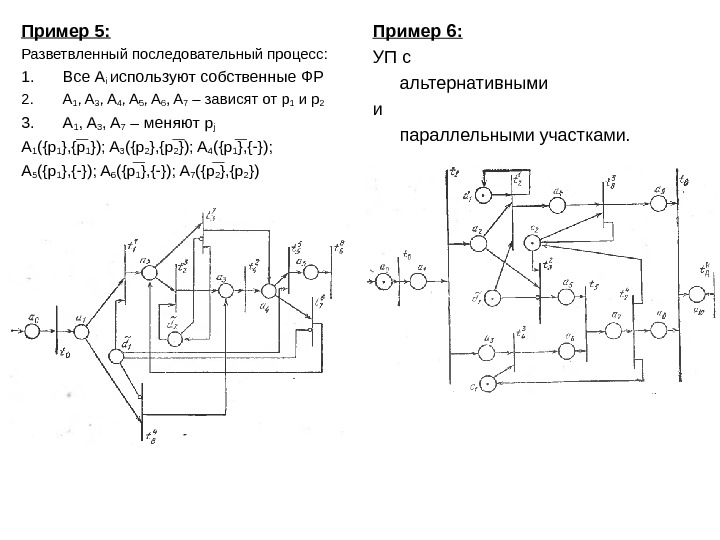
Пример 5: Разветвленный последовательный процесс: 1. Все A i используют собственные ФР 2. A 1 , A 3 , A 4 , A 5 , A 6 , A 7 – зависят от p 1 и p 2 3. A 1 , A 3 , A 7 – меняют p j A 1 ({p 1 }, {p 1 }); A 3 ({p 2 }, {p 2 }); A 4 ({p 1 }, {-}); A 5 ({p 1 }, {-}); A 6 ({p 1 }, {-}); A 7 ({p 2 }, {p 2 }) Пример 6: УП с альтернативными и параллельными участками.

Обобщенная сеть Петри для описания неавтономного управляющего процесса.

Автономный УП Неавтономный УП Описание неавтономного процесса: 1. внеш. ЛУ (pu ) ↔ внеш. позиция hu – метка есть, если p u =1 ; нет при pu =0 2. внеш. ЛУ ϵ {P 1 } 3. есть внутренние и внешние ЛУ 4. если A i выполняется при pu =1 (0) , то h u соединяется с tдi сдерживающей дугой 5. не включается позиция состояния внешнего ЛР 6. развитие процесса – зависит от начальной маркировки внутренних позиций и текущей маркировки внешних входных позиций 7. замена внешних входных позиций на предикаты, зависящие от внешних ЛУ Если не определено влияние A i на значение p s : 1. возможное изменение p s – это безразличное значение ( p s ) в {P 2i } 2. позиция состояния D s — в описании параллельного процесса 3. на время выполнения t дi метка из ds удаляется 4. позиция d s аналогична внешней позиции

Пример: ФР – собственные ЛР D 1 – внутренний ЛР D 2 – изменяется A 1 → изменяется p 2 Задано: A 2 ({p 1 }, {p 1 }) A 3 ({p 1 }, {-}) A 4 ({p 2 }, {-}) A 5 ({p 2 }, {-}) ЛР D 2 – счетчик → позиция d 2 — внутренняя k – константа для сравнения k -кратная дуга между a 5 и t

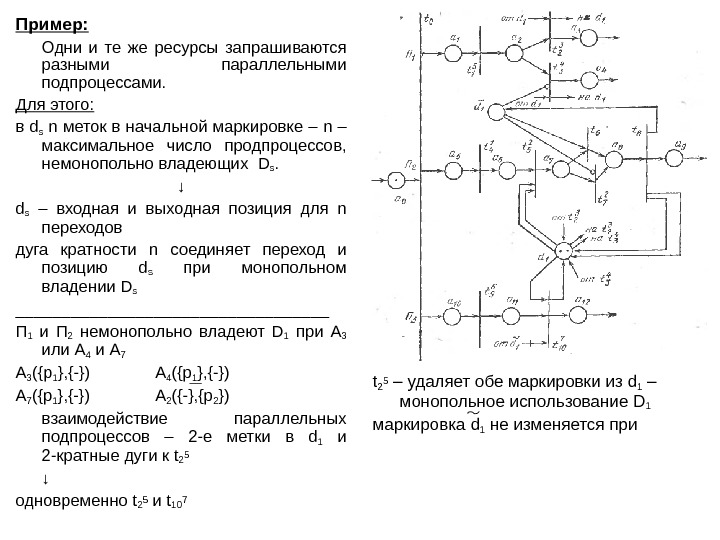
Пример: Одни и те же ресурсы запрашиваются разными параллельными подпроцессами. Для этого: в d s n меток в начальной маркировке – n – максимальное число продпроцессов, немонопольно владеющих D s. ↓ d s – входная и выходная позиция для n переходов дуга кратности n соединяет переход и позицию d s при монопольном владении D s _________________ П 1 и П 2 немонопольно владеют D 1 при A 3 или A 4 и А 7 A 3 ({p 1 }, {-}) A 4 ({p 1 }, {-}) A 7 ({p 1 }, {-}) A 2 ({-}, {p 2 }) взаимодействие параллельных подпроцессов – 2- е метки в d 1 и 2-кратные дуги к t 2 5 ↓ одновременно t 2 5 и t 10 7 t 25 – удаляет обе маркировки из d 1 – монопольное использование D 1 маркировка d 1 не изменяется при

Граф обобщенной сети Петри содержит: 1. длительные переходы 2. примитивные переходы 3. основные внутренние позиции 4. ресурсные внутренние позиции 5. основные дуги 6. неизменяющие дуги заданной 7. сдерживающие дуги кратности 8. длительный переход – это процедура 9. предикаты у tдi , если Ai зависит от внешних ЛУ 10. примитивные переходы – переходы распараллеливания и соединения – задание структуры процесса 11. маркировка a µ (основные) и cj , ds ( внутренние ресурсные) – полное состояние УП 12. дуги – последовательность выполнения процедур и их взаимодействие с ФР и ЛР. Свойства: Временных сетей с переходами, помеченными предикатами и операциями, и дугами разных типов. Особенность: 1. в описание процесса вводятся используемые им ресурс 2. учитывается влияние процедур процесса на состояние ресурсов

Получение правильного управляющего процесса. Граф достижимых маркировок сети Петри.

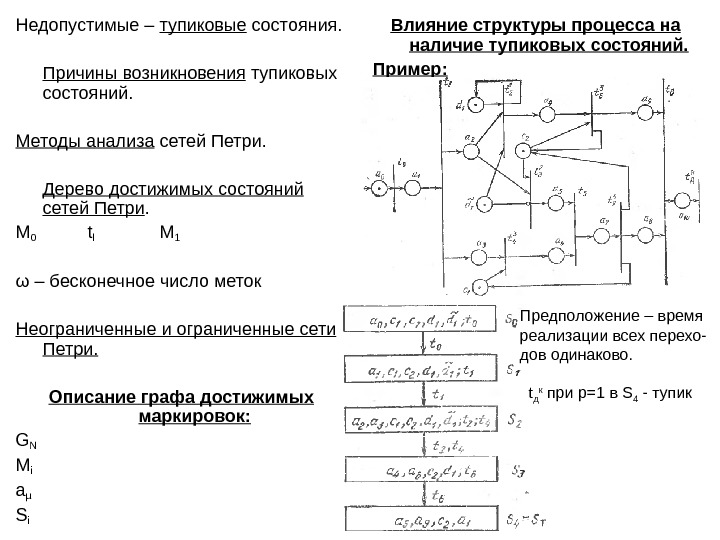
Недопустимые – тупиковые состояния. Причины возникновения тупиковых состояний. Методы анализа сетей Петри. Дерево достижимых состояний сетей Петри. М 0 tl М 1 ω – бесконечное число меток Неограниченные и ограниченные сети Петри. Описание графа достижимых маркировок: G N M i a µ S i Влияние структуры процесса на наличие тупиковых состояний. Пример: Предположение – время реализации всех перехо- дов одинаково. t д к при p=1 в S 4 — тупик

Для p=0 в начальной маркировке, т. е. в ds нет метки – вместо t 2 будет активизирован t 3. левая ветвь – p=1 правая ветвь – p=0 S 4 и S 7 – тупиковые Реализация активизированных переходов завершается одновременно. Это граф статических состояний процесса.

Это динамический граф. Исходящие дуги – переходы, переходящие в стадию реализации. Входящие дуги – переходы, закончившие реализацию. В скобках – переходы, продолжающие реализацию. ↓ Неустойчивые состояния. S 8 a 3 a 6 t 4 S 4 и S 7 – тупиковые Причина – недопустимая структура процесса. Граф, содержащий статические и промежуточные состояния.

Требования к правильной структуре процесса. Другая причина недостижимости конечного состояния – циклы. Пример: Для фиксированной начальной позиции d 1 и d 2. Полный граф достижимости

Пример: p 2 =1 D 2 – внешний ЛР Есть информация о D 2 и его взаимодействии с УП

Тупиковые состояния, вызываемые разделением функциональных ресурсов. Пример: П 1 и П 2 – асинхронные циклические процессы С 1 и С 2 – разделяемые ФР b 1 и b 2 – внешние входные позиции П 1 – по горизонтали П 2 – по вертикали S ij – вершины, состояния, где i – номер в П 1 , а j – в П

Классификация состояний в графе достижимых маркировок сети Петри. 1. Состояние блокировки – S б : a µ t i 2. Состояние взаимной блокировки – S в. б 3. Состояние полной взаимной блокировки – S п. в. б 4. Тупиковое состояние – S т – это S в. б и S п. в. б 5. Предтупиковое состояние – S п. т Q з {S т , S п. т } – множество запрещенных состояний 6. Опасное состояние — S оп , если: S v ребро S u и S v ϵ Q з , а S u ϵ Q з Q оп – множество опасных состояний 7. Безопасное состояние 8. Состояние конфликта – Sкн Опасные отрезки пути в графе Корень опасных отрезков – S к. оп Дополнительная блокирующая позиция – а б

Пример: