Презентация Лекция 2 Динамика full

Лекция № 2 ДИНАМИКА Динамика – это раздел механики, в котором изучают влияние взаимодействий между механическими системами на их механическое движение. Воздействие одного тела на другое при их взаимодействии описывается векторной величиной, определяющей и интенсивность и направление воздействия. Эта величина называется силой. Сила — векторная величина, выражающая внешнее воздействие на материальное тело, заставляющее его испытывать ускорение, т. е. является причиной неравномерного движения. В общем случае сила обозначается как , в системе СИ величина силы измеряется в Ньютонах (Н). F r Современные экспериментальные данные свидетельствуют, что существуют только четыре качественно различных вида взаимодействий , в которых участвуют элементарные частицы. Эти взаимодействия называют фундаментальными. Фундаментальные взаимодействия отличаются в количественном отношении по силе воздействия, характеризуемом термином «интенсивность» . По мере увеличения интенсивности взаимодействия фундаментальные взаимодействия располагаются в следующем порядке: гравитационное , слабое , электромагнитное и сильное.

Гравитационное взаимодействие является универсальным: в нем участвуют все без исключения физические объекты , в частности, все без исключения элементарные частицы. В случае, когда гравитационное поле является относительно слабым, а скорости физических объектов (тел, материальных точек, частиц) малы по сравнению со скоростью света в вакууме м/с, две материальные точки массами и притягивают друга силой ‘m»m 83 10 c 1 12 ‘ »m m F G r — открытый Ньютоном закон всемирного тяготения, где – величина силы гравитационного взаимодействия, r – расстояние между материальными точками, – гравитационная постоянная. Потенциальная энергия гравитационного взаимодействия 1 F 11 3 2 1 6, 67 10 м /(кг с )G 1 1 ‘ »m m U G r Модуль этой величины очень медленно падает с увеличением расстояния между материальными точками: 1~ 1 U r . В соответствии с этим гравитационные силы называют дальнодействующими.

Первая космическая скорость — скорость, которую необходимо придать объекту, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом равным радиусу планеты. Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите. Геостационарная орбита (ГСО) — круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой, искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси, и постоянно находится над одной и той же точкой на земной поверхности. км 786 353 22 2 M R R Mm Rmma

В электромагнитном взаимодействии участвуют все заряженные частицы и фотон (квант, порция электромагнитного излучения). Взаимодействие между атомами и молекулами – нейтральными образованиями, составленными из заряженных частиц, – определяется взаимодействием между заряженными частицами и носит электромагнитный характер, поэтому к электромагнитному взаимодействию сводится большинство сил, наблюдаемых в макроскопических явлениях: силы упругости, трения, поверхностного натяжения в жидкостях др. Фундаментальным законом в теории электромагнитного взаимодействия является закон Кулона. Две материальные точки с зарядами и (точечные заряды), находящиеся на расстоянии r друг от друга в вакууме взаимодействуют силой’q»q 22 ‘ »q q F k r 9 3 2 2 9 10 кг м /(Кл с )k Заряженные тела, отталкиваются, если заряды и одного знака, и притягиваются, если знаки зарядов противоположны. Закон Кулона так же как закон всемирного тяготения – используют, когда скорости зарядов малы по сравнению со скоростью света в вакууме.

где и – целые числа. Таким образом, заряд физического объекта фактически определяется величиной Z. Поэтому естественно переписать закон Кулона в виде Заряды тел, материальных точек кратны элементарному заряду Кл (заряд протона): 19 1, 6 10 e ‘ ‘q Z e » »q Z e ‘Z»Z 2 22 ‘ »Z Z F ke r или , 2 22 ‘ »Z Z F G r где 2 2 G ke – величина, аналогичная гравитационной постоянной 1 G Потенциальная энергия кулонова взаимодействия 2 2 ‘ »Z Z U G r откуда видно, что электромагнитные силы, как и гравитационные, являются дальнодействующими.

-распад — тип радиоактивного распада, изменяющего заряд ядра на единицу, при котором ядро может излучать бета-частицу (электрон или позитрон). Поток бета-частиц называется бета-лучи или бета-излучение. Кроме того, слабое взаимодействие играет важную роль в термоядерных реакциях, ответственных за выделение энергии в звездах. Слабое взаимодействие – в отличие от гравитационного и электромагнитного – является короткодействующим. Для таких взаимодействий вводят понятие « радиус действия сил » . Слабое взаимодействие присуще всем частицам, кроме фотона. Одно из макроскопических проявлений слабого взаимодействия Для дальнодействующих гравитационных и кулоновских сил соответствующие потенциальные энергии взаимодействия имеют вид 1 U r b r где b – постоянная величина, не зависящая от расстояния r между взаимодействующими объектами.

Пусть потенциальная энергия для некоторого взаимодействия определяется формулой r rf br. U )( )( где – постоянная, – функция, быстро убывающая с расстоянием r и . Для этой функции вводят характерный масштаб убывания : это такое расстояние, что . Если, например, ‘bf r 0 1 f 0 r)0()(0 frf exp *f r r r где – некоторая положительная постоянная с размерностью длины, то именно и есть характерный масштаб убывания функции : *r *r f r 0*r r В самом деле, 0 exp 1 1 3 f r если взять r на порядок больше, то и 010 r r 5105, 4)(rf взаимодействием можно пренебречь. Характерный масштаб называется радиусом действия сил. 0 r

Сильное взаимодействие удерживает положительно заряженные протоны и незаряженные нейтроны в ядрах атомов и, таким образом, является ответственным за стабильность атомных ядер. Оно обладает свойством зарядовой независимости : взаимодействия в парах протон-протон, нейтрон-нейтрон и протон-нейтрон одинаковы. Протоны и нейтроны – частицы, из которых состоят атомные ядра, –носят название нуклонов (ядерных частиц). Сильное взаимодействие является короткодействующим. В теории сильного взаимодействия, сформулированной Юкавой еще в 1935 г. , предполагается, что взаимодействие между неподвижными нуклонами можно описать с помощью потенциальной энергии взаимодействияr rr gr. U )/exp( )( 02 где g – константа связи сильного взаимодействия, м – радиус действия ядерных сил, равный по порядку величины характерному размеру ядра. Известным макроскопическим проявлением сильного взаимодействия является альфа-распад — вид радиоактивного распада ядра, в результате которого происходит испускание альфа-частицы — положительно заряженной частицы, образованной 2 протонами и 2 нейтронами. 15 0~ 10 r

Законы Ньютона справедливы в инерциальных системах отсчета Инерциальная система отсчета (ИСО) — система отсчёта, в которой справедлив закон инерции: любое тело, на которое не действуют внешние силы, находится в состоянии покоя или равномерного прямолинейного движения. В механике эквивалентность ИСО выражается принципом относительности Галилея , который гласит: во всех инерциальных системах отсчета любой механический процесс протекает одинаково, вследствие чего никакими механическими опытами невозможно идентифицировать инерциальную систему отсчета. В силу важности принципа относительности Галилея его формулировка в другой редакции: законы механики во всех инерциальных системах отсчета имеют один и тот же вид. Первый закон Ньютона гласит: существуют инерциальные системы отсчёта, в которых замкнутая система продолжает оставаться в состоянии покоя или прямолинейного равномерного движения. Замкнутая система — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют или скомпенсированы.

Ускорение, сообщаемое силой материальной точке массы m , сонаправлено с силой, а его величина пропорциональна величине силы и обратно пропорциональна массе материальной точки: F r Многочисленные экспериментальные данные позволили Ньютону сформулировать закон, являющийся основой динамики , так называемый второй закон Ньютона. Он гласит: F a k m r r где k – положительный коэффициент, зависящий от выбора системы единиц. В системе СИ этот коэффициент равен безразмерной единице, таким образом, второй закон Ньютона в традиционной форме: ma F rr В случае, когда на материальную точку действуют одновременно две или несколько ( n ) сил, для определения ускорения следует использовать принцип суперпозиции сил , который гласит: Ускорение, приобретаемое материальной точкой под действием двух или нескольких сил, равно сумме ускорений, сообщаемых материальной точке каждой из сил в отдельности.

1 2. . . n ma F F F r r rr. Используя символ суммирования, n i iam. FF 1 равн (1) Равнодействующая сила — векторная сумма всех приложенных к телу сил. равн. F Таким образом, чтобы определить ускорение материальной точки, необходимо сложить (геометрически!) все силы, действующие на нее, и поделить результат на массу материальной точки. Закон (1) имеет один и тот же вид во всех инерциальных системах отсчета. В случае, если масса тела меняется со временем, то второй закон Ньютона можно сформулировать следующим образом: скорость изменения импульса тела равна действующей на тело силе: dt pd

Третий закон Ньютона : тела действуют друг на друга с силами, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению. Так как эти силы приложены к разным телам – они не компенсируются. Краткая запись третьего закона Ньютона, 12 21 F F r r В общем случае, если на тело действует некоторая сила , то эта сила имеет источник воздействия – другое тело (материальная точка, система), на которое со стороны первого тела одновременно действует сила , причем такая что Например, на летящую муху со стороны Земли действует гравитационная сила , где m – масса мухи. На Землю со стороны мухи действует сила F r ‘F F r r F mg rr ‘F mg r r

Третий закон Ньютона имеет место только в нерелятивистской механике, т. е. при условии малых скоростей механических систем . В релятивистской физике воздействие одной системы на другую реализуется принципиально посредством силового поля , возмущения которого распространяются с конечной скоростью; третий закон Ньютона при этом не работает. Все, что здесь сказано, относится к инерциальным системам отсчета ( ИСО ). В дальнейшем следует иметь ввиду, что по умолчанию рассмотрение физических процессов проводится в ИСО. c. V

Динамика материальной точки Применение второго закона Ньютона

Дано: = 600 м/c m=4, 65 10 -26 кг =60 0 F t — ? Решение. А 1. Молекула массой m = 4, 65 10 -26 кг, летящая со скоростью = 600 м/c, ударяется о стенку сосуда под углом = 60 0 к нормали и упруго отскакивает от нее без потери скорости. Найти импульс силы , полученный стенкой за время удара. Используем второй закон Ньютона. dp F dt rr Импульсом силы называется величина. Fdt dp rr Найдём приращение импульса 2 1. dp p p r r r В проекциях на оси координат 2 1, x x xdp p p 2 1. y y ydp p p 2 1 x x xdp p p cosp p 2 cos. mv 2 1 y y ydp p p sinp p 0.

Решение (продолжение)А 1. Молекула массой m = 4, 65 10 -26 кг, летящая со скоростью = 600 м/c, ударяется о стенку сосуда под углом = 60 0 к нормали и упруго отскакивает от нее без потери скорости. Найти импульс силы , полученный стенкой за время удара. 2 12 cos. x x xdp p p mv Знак «-» у проекции на ось OX и равенство нулю проекции на ось OY означает, что приращение импульса и сила, действующая на молекулу, направлена «от стенки» (см. рис. ). В то же время, сила, действующая на стенку со стороны молекулы, направлена в противоположную сторону. 26 23 2 cos 2 4, 65 10 600 0, 5 2, 8 10. кг м Fdt mv с r Ответ: 23 2, 8 10. кг м с

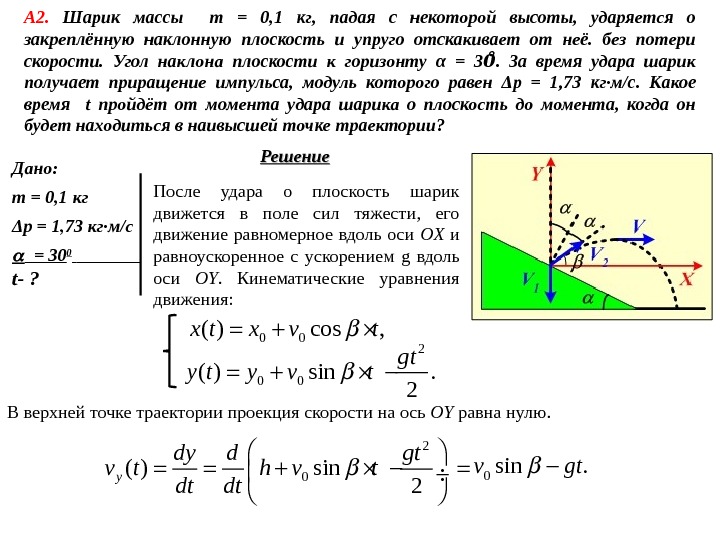
Дано: m = 0, 1 кг Δ p = 1, 73 кг·м/с = 30 0 t — ? Решение. А 2. Шарик массы m = 0, 1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 3. За время удара шарик 00 получает приращение импульса, модуль которого равен Δ p = 1, 73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории? После удара о плоскость шарик движется в поле сил тяжести, его движение равномерное вдоль оси OX и равноускоренное с ускорением g вдоль оси OY. Кинематические уравнения движения: 2 0 0( ) sin. 2 gt y v t 0 0( ) cos , x t x v t В верхней точке траектории проекция скорости на ось OY равна нулю. 2 0( ) sin 2 y dy d gt v t h v t dt dt 0 sin. v gt

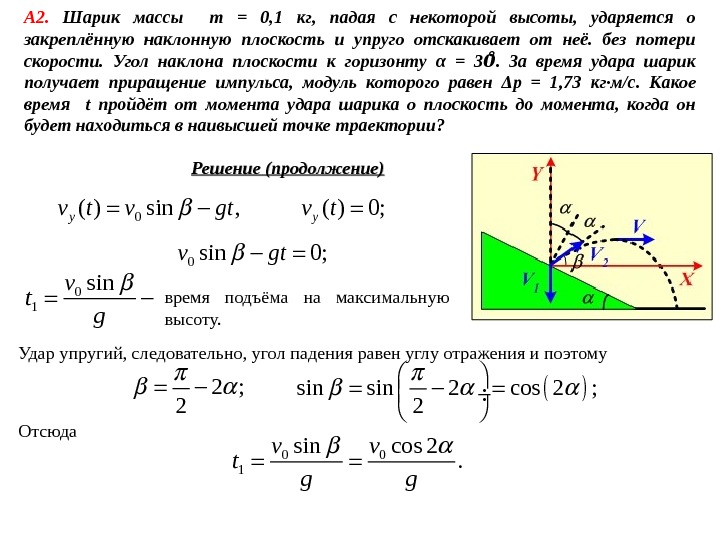
Решение (продолжение)А 2. Шарик массы m = 0, 1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 3. За время удара шарик 00 получает приращение импульса, модуль которого равен Δ p = 1, 73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории? 0( ) sin , yv t v gt 0 sin 0; v gt ( ) 0; yv t 0 1 sinv t g время подъёма на максимальную высоту. Удар упругий, следовательно, угол падения равен углу отражения и поэтому 2 ; 2 sin 2 cos 2 ; 2 Отсюда 0 0 1 sin cos 2. v v t g g

Решение (продолжение)А 2. Шарик массы m = 0, 1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 3. За время удара шарик 00 получает приращение импульса, модуль которого равен Δ p = 1, 73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории? 1 2 0. V V V r r 22. x yp p p r Скорость V 0 найдём, рассмотрев удар шара о плоскость. Удар абсолютно упругий, поэтому модуль скорости остаётся неизменным. 2 1 y y yp p p 0 0 cos cosmv mv 02 cos. mv 2 1 x x xp p p 0 0 sin sinmv mv 0. 02 cos. p mv r Отсюда 0. 2 cos p v m

Решение (продолжение)А 2. Шарик массы m = 0, 1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 3. За время удара шарик 00 получает приращение импульса, модуль которого равен Δ p = 1, 73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории? Подставим полученное выражение для скорости в формулу для времени подъёма на максимальную высоту. 0 1 cos 2. 2 cos vp t g mg 1 1, 73 0, 5. 2 0, 1 9, 8 0, 866 t c Ответ: 0, 5 с.

Дано: = 30 ◦ = 45 ◦ m 1 = m 2 = 1 кг T — ? Решение. А 3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0 . Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь Если массой блока можно пренебречь, то ускорение можно найти из второго закона Ньютона. Для тела 1: 1 1 1. m a N T m g r rr r Предположим, что система движется справа налево на рисунке. Перепишем это уравнение в проекциях на оси (см. рис. ) : 1 1 sin , m a T m g : OX : OY 1 10 cos. N m g Трения нет, поэтому ускорение первого тела определяется только проекциями сил на ось OX . 1 1 sin. m a T m g

Решение (продолжение)А 3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0 . Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь Уравнение второго закона Ньютона для тела 2: 2 2 2. m a N T m g r rr r Тела связаны нерастяжимой нитью, поэтому 2 2 sin , m a T m g : OX : OY 2 20 cos. N m g Это же уравнение в проекциях на оси: Трения нет, поэтому ускорение первого тела определяется только проекциями сил на ось OX . 2 2 sin. m a T m g 2 1 2. a a r r Обозначим 1 2. a a a r r

Решение (продолжение)А 3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0 . Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь Если массой блока можно пренебречь, то согласно третьему закону Ньютона 1 2. T T r r Подставим введённые обозначение в (1) и (2): 1 1 sin , m a T m g Обозначим 1 2. T T T r r 2 2 sin. m a T m g Сложим первое и второе уравнения: 1 2 sin , m m a m g 1 2 sin. m m a g m m

А 3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0 . Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь Подставим полученное выражение для ускорения в первое уравнение системы: Решение (продолжение) 1 1 sin , m a T m g 2 2 sin. m a T m g 1 2 1 1 1 2 sin sin. m m m g T m g m m 1 2 1 1 1 2 sin sin m m T m g m m 1 2 1 1 2 sin sin m m m g m m 1 2 1 1 2 sin sinm m m g m m 2 2 1 1 2 sinm m m g m m 1 2 sin. m m g m m

Решение (продолжение) Выполним вычисления: 1 2 2 1 1 1 sin 2 29, 8 0, 24. 1 1 m mм a g m mс А 3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 30 0 и = 45 0 . Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь 1 2 1 sin 9, 8 6. 1 1 2 2 m m T g. Н m m

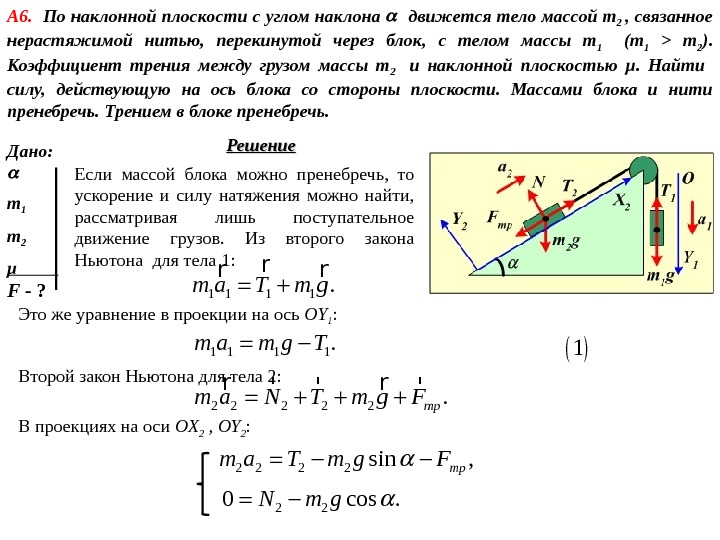
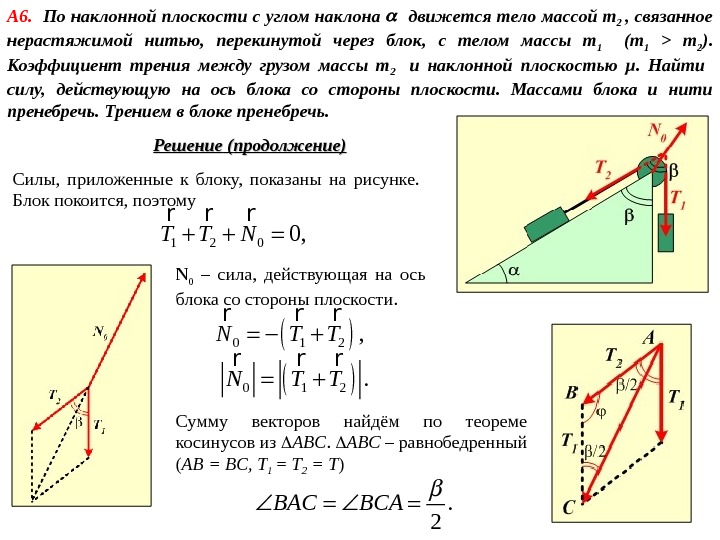
Дано: m 1 m 2 μ F — ? Решение. А 6. По наклонной плоскости с углом наклона движется тело массой m 2 , связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Если массой блока можно пренебречь, то ускорение и силу натяжения можно найти, рассматривая лишь поступательное движение грузов. Из второго закона Ньютона для тела 1: 1 1. m a T m g rr r Это же уравнение в проекции на ось OY 1 : 1 1. m a m g T Второй закон Ньютона для тела 2: 2 2 2. трm a N T m g F r r rr r 1 В проекциях на оси OX 2 , OY 2 : 2 2 sin , трm a T m g F 2 2 0 cos. N m g

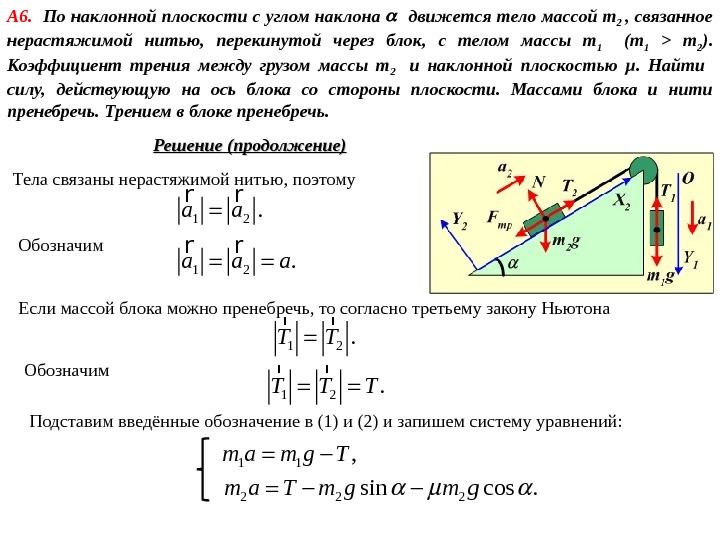
Решение ( ( продолжение)А 6. По наклонной плоскости с углом наклона движется тело массой m 2 , связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Величина силы трения скольжения равна. тр. F N Из второго уравнения системы: 2 Тогда первое уравнение системы принимает вид: 2 2 sin , трm a T m g F 2 2 0 cos. N m g 2 2 cos. N m g 2 cos. тр. F N m g 2 2 2 sin cos. m a T m g

А 6. По наклонной плоскости с углом наклона движется тело массой m 2 , связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Решение ( ( продолжение) Тела связаны нерастяжимой нитью, поэтому 1 2. a a r r Обозначим 1 2. a a a r r Если массой блока можно пренебречь, то согласно третьему закону Ньютона 1 2. T T r r Подставим введённые обозначение в (1) и (2) и запишем систему уравнений: Обозначим 1 2. T T T r r 2 2 2 sin cos. m a T m g 1 1, m a m g T

А 6. По наклонной плоскости с углом наклона движется тело массой m 2 , связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Решение ( ( продолжение) Из этой системы уравнений найдём силу натяжения. Разделим первое уравнение на второе: 2 2 2 sin cos. m a T m g 1 1, m a m g T 1 1 2 2 2. sin cosm m g T m g m g 1 2 2 2 1 sin cos , m T m g m m g T 1 1 2 1 2 2 sin cos , m T m m g m T 1 2 sin cos 1 , T m m g 1 2 sin cos 1. m m T g m m

А 6. По наклонной плоскости с углом наклона движется тело массой m 2 , связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Решение ( ( продолжение) Силы, приложенные к блоку, показаны на рисунке. Блок покоится, поэтому 1 2 00, T T N r r r N 0 – сила, действующая на ось блока со стороны плоскости. Сумму векторов найдём по теореме косинусов из ABC – равнобедренный ( AB = BC, T 1 = T 2 = T ) 0 1 2, N T T r r r 0 1 2. N T T r r r.

А 6. По наклонной плоскости с углом наклона движется тело массой m 2 , связанное нерастяжимой нитью, перекинутой через блок, с телом массы m 1 (m 1 > m 2 ). Коэффициент трения между грузом массы m 2 и наклонной плоскостью μ. Найти силу, действующую на ось блока со стороны плоскости. Массами блока и нити пренебречь. Трением в блоке пренебречь. Решение ( ( продолжение) 2. 2 ABC 2 2 2 02 cos. N T T T 2 2 1 cos. T 2 2 sin 2 2 T 2 sin , 2 2 T . 2 0 2 sin. 4 2 N T Ответ: 0 2 sin. 4 2 N T 1 2 sin cos 1 , m m T g m m

Дано: m 1 =10 т m 2 =5 т m 3 =100 кг 0 =500 м/с u 1 — ? Решение. А 5 а. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа стояла неподвижно. Согласно закону сохранения импульса, записанному в лабораторной системе отсчёта 1 2 1 3 3 0 , m m u r r — скорость платформы после выстрела, — скорость снаряда после выстрела в лабораторной системе отсчёта. 3 u r 1 u r В лабораторной системе отсчёта скорость снаряда 3 0 1. u v u r r r 1 2 1 3 30. x x m m u 1 2 1 3 0 10 , x xm m u m v u В лабораторной системе отсчёта в проекциях на ось OX

Решение (продолжение)А 5 а. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа стояла неподвижно. Откуда проекция скорости платформы после выстрела 1 2 1 3 0 10 , m m u m v u 3 0 1 1 2 3. x m v u m m m Скорость платформы после выстрела направлена против оси OX ( влево на рисунке ). 3 3 0 13 1 2 3 0, 1 10 500 3, 3. 10 5 0, 1 10 x m vм u m m mс Ответ: 13, 3. x м u с

Решение. А 5 б. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа двигалась со скоростью =18 км/ч и выстрел был произведен в направлении ее движения. Дано: m 1 =10 т m 2 =5 т m 3 =100 кг =18 км/ч 0 =500 м/с u 1 — ? Согласно закону сохранения импульса, записанному в лабораторной системе отсчёта 1 2 3 1 2 1 3 3, m m m v m m u r r r — скорость платформы после выстрела, — скорость снаряда после выстрела в лабораторной системе отсчёта. 3 u r 1 u r В лабораторной системе отсчёта скорость снаряда 3 0 1. u v u r r r 1 2 3 1 2 1 3 3. x x xm m m v m m u 1 2 3 1 2 1 3 0 1, x xm m m v m m u m v u В лабораторной системе отсчёта в проекциях на ось OX

Решение (продолжение)А 5 б. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа двигалась со скоростью =18 км/ч и выстрел был произведен в направлении ее движения. Откуда проекция скорости платформы после выстрела 1 2 3 3 0 1 1 2 3. x x x m m m v u m m m Проекции скоростей на ось OX : 3 3 1 2 3 3 0 13 1 2 3 10 5 0, 1 10 500 1, 7. 10 5 0, 1 10 x x m m m vм u m m mс Ответ: 11, 7. x м u с 1 2 3 1 2 1 3 0 1 , x xm m m v m m u m v u 18 5 , x км м v v ч с 0 0 500. x м v v с

Решение. А 5 в. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа двигалась со скоростью =18 км/ч и выстрел был произведен в направлении, противоположном направлению ее движения. Дано: m 1 =10 т m 2 =5 т m 3 =100 кг =18 км/ч 0 =500 м/с u 1 — ? Согласно закону сохранения импульса, записанному в лабораторной системе отсчёта 1 2 3 1 2 1 3 3, m m m v m m u r r r — скорость платформы после выстрела, — скорость снаряда после выстрела в лабораторной системе отсчёта. 3 u r 1 u r В лабораторной системе отсчёта скорость снаряда 3 0 1. u v u r r r 1 2 3 1 2 1 3 3. x x xm m m v m m u 1 2 3 1 2 1 3 0 1, x xm m m v m m u m v u В лабораторной системе отсчёта в проекциях на ось OX

Решение (продолжение)А 5 в. На рельсах стоит платформа массой m 1 =10 т. На платформе закреплено орудие массой m 2 =5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m 3 =100 кг; его начальная скорость относительно орудия 0 =500 м/с. Найти скорость u 1 платформы в первый момент после выстрела, если платформа двигалась со скоростью =18 км/ч и выстрел был произведен в направлении, противоположном направлению ее движения. Откуда проекция скорости платформы после выстрела 1 2 3 3 0 1 1 2 3. x x x m m m v u m m m Проекции скоростей на ось OX : 3 3 1 2 3 3 0 13 1 2 3 10 5 0, 1 10 500 8, 3. 10 5 0, 1 10 x x m m m vм u m m mс Ответ: 11, 7. x м u с 1 2 3 1 2 1 3 0 1 , x xm m m v m m u m v u 18 5 , x км м v v ч с 0 0 500. x м v v с Скорость платформы после выстрела направлена против оси OX ( влево на рисунке ).

А 6. Граната, летевшая со скоростью v = 10 м/с, разорвалась на два осколка. Большой осколок, масса которого составила 0, 6 массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью u 1 = 25 м/с. Найти скорость u 2 малого осколка гранаты. Дано: m 1 = 0, 6 т m 2 =0, 4 т v = 10 м/с u 1 = 2 5 м/с u 2 — ? Решение Выберем ось OX направленной вдоль первоначального направления движения гранаты. В проекциях на оси координат закон сохранения импульса имеет вид: Согласно закону сохранения импульса 1 1 2 2. mv m u r r r 1 1 2 2 , x x xmv m u 1 1 2 2. y y ymv m u В выбранной нами системе отсчёта по условию задачи 0, yv 10. yu Из последнего уравнения следует, что 20. yu Это означает, что оба осколка после взрыва движутся вдоль оси OX , хотя, возможно, и в разных направлениях. Из уравнения для проекций импульсов на ось OX 2 2 1 1 , x x xm u mv m u

А 6. Граната, летевшая со скоростью v = 10 м/с, разорвалась на два осколка. Большой осколок, масса которого составила 0, 6 массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью u 1 = 25 м/с. Найти скорость u 2 малого осколка гранаты. Решение ( ( продолжение) В выбранной нами системе отсчёта 2 2 1 1 , x x xm u mv m u 1 1 2 2 x x x mv m u u m 1 0, 6 0, 4 x xmv mu m 10, 6. 0, 4 x xv u 10 , x м v v с 1 1 25. x м u u с 1 2 0, 6 10 0, 6 25 10. 0, 4 x x xv u м u с Это означает, что меньший осколок полетит в направлении, противоположном первоначальному направлению движения гранаты. Ответ: 110. x м u с

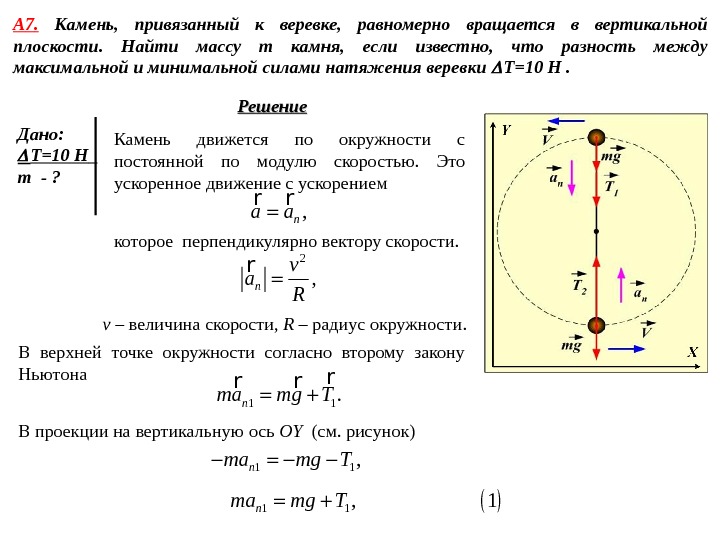
А 7. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу m камня, если известно, что разность между максимальной и минимальной силами натяжения веревки T=10 Н . Дано: T=10 Н m — ? Решение Камень движется по окружности с постоянной по модулю скоростью. Это ускоренное движение с ускорением , na a r r которое перпендикулярно вектору скорости. 2 , n v a Rr v – величина скорости, R – радиус окружности. В верхней точке окружности согласно второму закону Ньютона 1 1. nma mg T r r r В проекции на вертикальную ось OY ( см. рисунок) 1 1 , nma mg T

А 7. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу m камня, если известно, что разность между максимальной и минимальной силами натяжения веревки T=10 Н . Решение (продолжение) В нижней точке окружности согласно второму закону Ньютона 2 2. nma mg T r r r В проекции на вертикальную ось OY ( см. рисунок) 2 2. nma mg T 1 , n. T ma mg 2 Величина a n зависит только от скорости и радиуса, а их величины по условию постоянны, поэтому 1 2. n n na a a Из уравнений (1) и (2) выразим величины сил натяжения и учтём, что величина нормального ускорения постоянна: 2. n. T ma mg

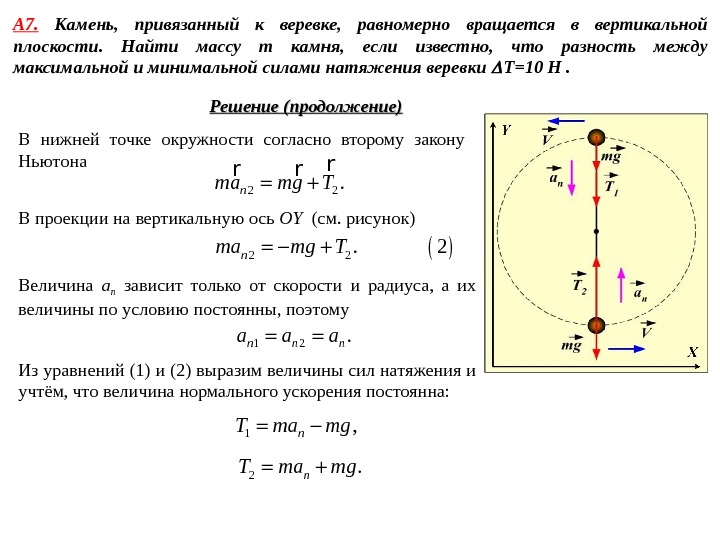
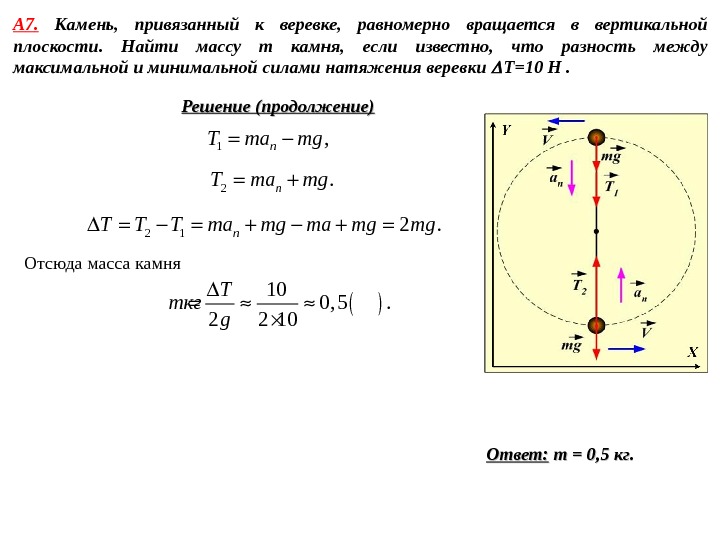
А 7. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу m камня, если известно, что разность между максимальной и минимальной силами натяжения веревки T=10 Н . Решение (продолжение) Отсюда масса камня 1 , n. T ma mg 2 1 2. n. T T T ma mg mg 10 0, 5. 2 2 10 T m кг g Ответ: m = 0, 5 кг.

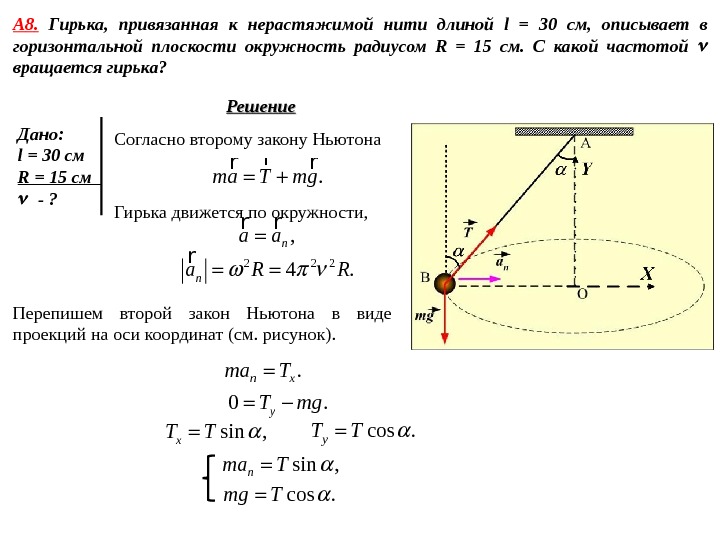
А 8. Гирька, привязанная к нерастяжимой нити длиной l = 30 см, описывает в горизонтальной плоскости окружность радиусом R = 15 см. С какой частотой вращается гирька? Дано: l = 30 см R = 15 см — ? Решение Согласно второму закону Ньютона . ma T mg r r r Гирька движется по окружности, , na a r r 2 2 2 4. na R R r Перепишем второй закон Ньютона в виде проекций на оси координат (см. рисунок). . n xma T 0. y. T mg sin , x. T T cos. y. T T sin , nma T cos. mg T

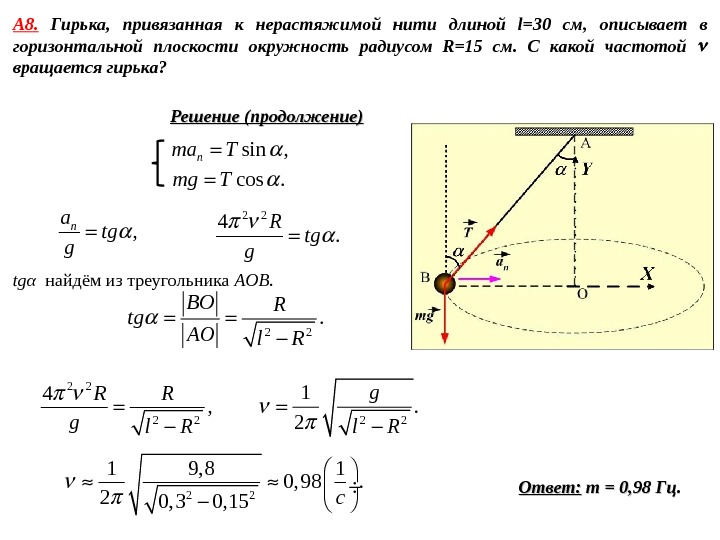
А 8. Гирька, привязанная к нерастяжимой нити длиной l=30 см, описывает в горизонтальной плоскости окружность радиусом R=15 см. С какой частотой вращается гирька? Решение (продолжение) sin , nma T cos. mg T , na tg g 2 2 4. R tg g tg α найдём из треугольника AOB. 2 2. BO R tg AO l R 2 24 , R R g l R 2 21. 2 g l R 2 21 9, 8 1 0, 98. 2 0, 3 0, 15 c Ответ: m = 0, 9898 Гц.

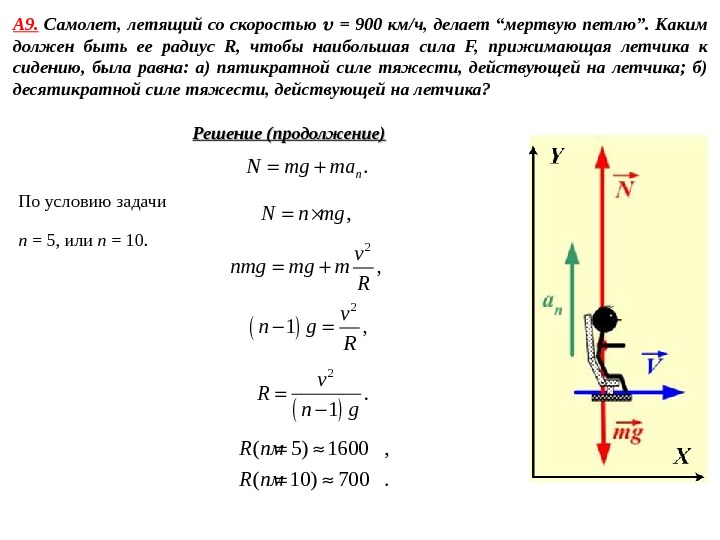
А 9. Самолет, летящий со скоростью = 900 км/ч, делает “мертвую петлю”. Каким должен быть ее радиус R, чтобы наибольшая сила F, прижимающая летчика к сидению, была равна: а) пятикратной силе тяжести, действующей на летчика; б) десятикратной силе тяжести, действующей на летчика? Дано: = 900 км/ч а) F= 5 mg б) F = 10 mg R — ? Решение Согласно третьему закону Ньютона «прижимающая» сила F равна по величине силе реакции N. . F N r r В нижней точке «мёртвой петли» согласно второму закону Ньютона. nma mg N r r r В проекции на вертикальную ось OY ( см. рисунок). nma mg N . n. N mg ma Отсюда

А 9. Самолет, летящий со скоростью = 900 км/ч, делает “мертвую петлю”. Каким должен быть ее радиус R, чтобы наибольшая сила F, прижимающая летчика к сидению, была равна: а) пятикратной силе тяжести, действующей на летчика; б) десятикратной силе тяжести, действующей на летчика? Решение (продолжение). n. N mg ma По условию задачи , N n mg n = 5, или n = 10. 2 , v nmg mg m R 2 1 , v n g R 2. 1 v R n g ( 5) 1600 , ( 10) 700. R n м

A 10. Искусственный спутник Земли движется по круговой орбите в плоскости экватора с запада на восток. На какой высоте h от поверхности Земли должен находиться этот спутник, чтобы он был неподвижен по отношению к наблюдателю, находящемуся на поверхности Земли у экватора? Дано: m = 6· 10 24 кг R = 6380 км Решение T = 24 ч h — ? На спутник действует сила тяжести, которая второму закону Ньютона создаёт нормальное (центростремительное) ускорение. Если ось OY направить по направлению ускорения (см. рисунок), то 2 , n m. M ma G r где m – масса спутника, M – масса Земли, r – радиус орбиты. , r R h где R – радиус Земли, r – радиус орбиты , h – высота. 2 , n M a G R h 2 2 24 , na r R h T

A 10. Искусственный спутник Земли движется по круговой орбите в плоскости экватора с запада на восток. На какой высоте h от поверхности Земли должен находиться этот спутник, чтобы он был неподвижен по отношению к наблюдателю, находящемуся на поверхности Земли у экватора? Решение (продолжение) 2 2 24 , M R h G T R h 2 3 2 , 4 GMT R h 2 3 2. 4 GMT h R 2 11 24 6 7 3 26, 67 10 6 10 24 3600 6, 38 10 3, 6 10 36000. 4 h м км