Презентация лекции 5 Группы И-80 90 11 марта

Презентация лекции 5 Группы И-80, 90 11 марта 2013 г.

Моделирование иерархической двухуровневой системы

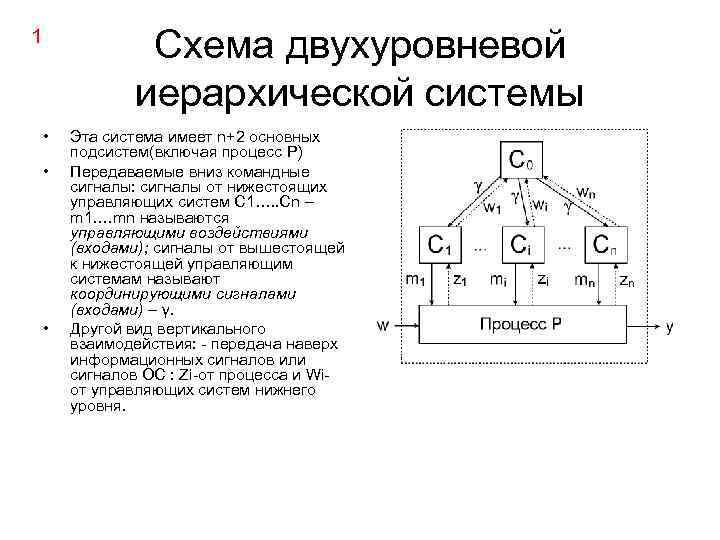Схема двухуровневой иерархической системы 1 • • • Эта система имеет n+2 основных подсистем(включая процесс Р) Передаваемые вниз командные сигналы: сигналы от нижестоящих управляющих систем С 1…. . Сn – m 1…. mn называются управляющими воздействиями (входами); сигналы от вышестоящей к нижестоящей управляющим системам называют координирующими сигналами (входами) – γ. Другой вид вертикального взаимодействия: - передача наверх информационных сигналов или сигналов ОС : Zi-от процесса и Wiот управляющих систем нижнего уровня.

2 Упрощенное описание двухуровневой системы • Процесс Р представлен в виде отражения P: M×Ω У, где m€M – множество управляющих сигналов (входов), w€Ω – входящие возмущения из внешней среды. • Так как имеется n нижестоящих локальных управляющих систем. То удобно представить множество управляющих сигналов M в виде M= M 1×M 2×…×Mn • Управляющая система реализует отображения : Ci : ξ ×Z Mi , где γ€ξ – координирующие сигналы; z€Z – обратные связи от процесса. Можно считать координирующие сигналы γ из ξ nмерными векторами (γ 1, …. , γn). • Рассматривается только один вход для системы Со – информация w от нижестоящих элементов посредством обратной информационной связи. Тогда по сути управляющая система Со осуществляет отображение Со : W ξ , где w€W – множественное отображение сигналов от Сi. • Сигналы обратной связи Zi, поступающие на вход локальной управляющей системы fi: ξ×Z×M →V.

3 Декомпозиция подсистем управляемого процесса • • процесс Р декомпозируется на n взаимосвязанных подпроцессов, каждый из которых задается отображением: Pi : Mi×Ui×Ω→Yi Здесь Ui – множество входных сигналов, посредством которых подпроцесс Pi связан с другими подроцессами. Hi : M×Y→Ui - связующие функции подпроцессов При правильном разбиении на связанные подпроцессы справедливо условие: Y= p(m, H(m, y), w)↔ y=p(m, w), которое выполняется для всех m, y, w.

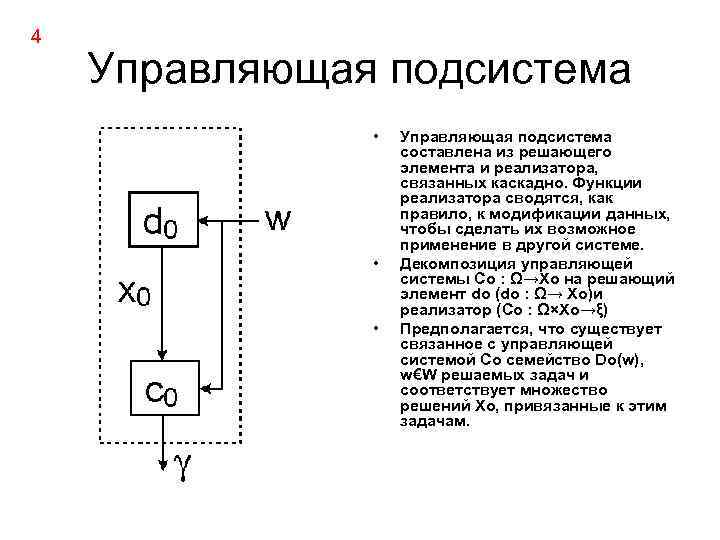4 Управляющая подсистема • • • Управляющая подсистема составлена из решающего элемента и реализатора, связанных каскадно. Функции реализатора сводятся, как правило, к модификации данных, чтобы сделать их возможное применение в другой системе. Декомпозиция управляющей системы Со : Ω→Xo на решающий элемент do (do : Ω→ Xo)и реализатор (Со : Ω×Xo→ξ) Предполагается, что существует связанное с управляющей системой Со семейство Do(w), w€W решаемых задач и соответствует множество решений Xo, привязанные к этим задачам.

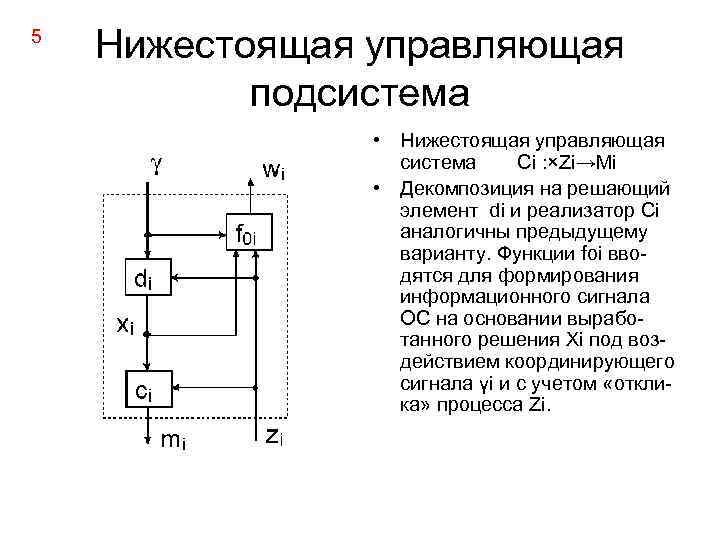5 Нижестоящая управляющая подсистема • Нижестоящая управляющая система Сi : ×Zi→Mi • Декомпозиция на решающий элемент di и реализатор Ci аналогичны предыдущему варианту. Функции foi вводятся для формирования информационного сигнала ОС на основании выработанного решения Xi под воздействием координирующего сигнала γi и с учетом «отклика» процесса Zi.

6 Прогнозирование взаимодействий • Предположим, что координатор прогнозирует будущие значения связующих сигналов. Т. е. несет в себе прогнозные значения • Простейшая форма принципа прогнозирования задается выражением: (1) • Здесь – фактические значения связующих входов. • Принцип просто утверждает, что подлежащая решению глобальная задача D разрешается с помощью управляющего воздействия всякий раз, когда «x» является решением задач, поставленных перед нижестоящими элементами и правильно прогнозируются взаимодействия.

7 Оценка взаимодействий • Это выражение прямо вытекает из (1) при замене прогнозного значения на интервальное (2)

8 Согласование (развязывание) взаимодействий • В этом случае успех координации оценивается исходя из расхождений или согласованности между фактическими взаимодействиями и теми, которые были бы желательны с токи зрения нижестоящих решающих элементов. (3) • Здесь – желаемые связующие сигналы нижестоящих элементов.

9 Координируемость • Под координированием понимают такое воздействие на элементы системы, которое заставляет их «действовать согласованно» . Чтобы сделать это определение более рациональным, нужно расшифровать эти два последних слова: «Действовать согласованно» . • В общем случае, координирование осуществляется в связи с определенной целью или задачей, и деятельность частей организации координируется ради этой общей цели или задачи в интересах организации в целом. Такую задачу мы будем называть глобальной решаемой задачей.

10 Координация по отношению к задаче вышестоящего элемента • Сигналы вышестоящего координирующего элемента являются непосредственно координирующими для нижестоящих решающих элементов, т. е. ξ =Xo • Задачи, решаемые элементами С 1, …, Сn, координируемы по отношению к задаче вышестоящего элемента тогда и только тогда, когда справедливо следующее соотношение: • [P(x, D(γ)) и P(γ, Do)] (4) • Следовательно необходимо, чтобы задача вышестоящего элемента имела решение и для некоторого координирующего входа γ, являющегося решением этой задачи, множество задач D(γ), решаемых нижестоящими элементами также имело решение.

11 Координация по отношению к глобальной задаче • Глобальная задача определяется, как правило, для всего процесса, поэтому ее решением можно считать «множество управляющих» М. • При предположении фиксированного характера информации, поступающей через каналы ОС, управляющие сигналы М исходят только от нижестоящих решающих элементов. Представим поэтому эти управляющие сигналы как отображения: Пм : X→M • Тогда задачи, решаемые нижестоящими элементами по отношению к глобальной задаче координируемы к ней тогда, когда справедливо следующее выражение: • [P(x, D(γ)) и P(Пм(x), D)] (5) • Такая координируемость просто означает, что координатор может влиять на нижестоящие элементы так, чтобы их результирующее воздействие на процесс в целом давало решение глобальной задачи.

12 Постулат совместимости • Для совместимости решаемых задач, а тем самым и целой внутри двухуровневой системы, координация задач, решаемых нижестоящими элементами, относительно задачи вышестоящего решающего элемента должна быть соответствующим образом связана с подлежащей решению глобальной задачей. Это можно формально записать следующим образом: (6) • • Решаемые на нижнем уровне локальные задачи скоординированы относительно решаемой глобальной задачи всякий раз, когда они скоординированы относительно задачи, решаемой на уровне вышестоящего элемента. • Если решаемые данной двухуровневой системой задачи совместимы, то глобальная цель достигается тогда, когда вышестоящий решающий элемент координирует нижестоящие элементы по отношению к его собственной цели