Презентация курса Термодинамика часть2 Истечение газов и

Презентация курса «Термодинамика» (часть2)

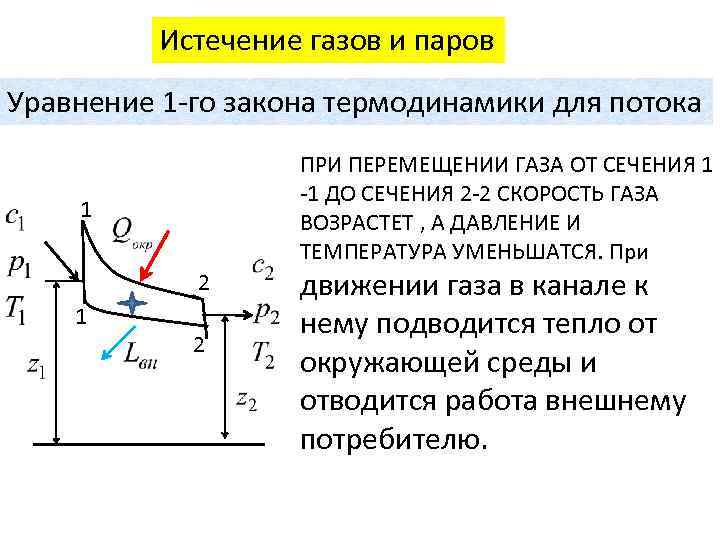Истечение газов и паров Уравнение 1 -го закона термодинамики для потока ПРИ ПЕРЕМЕЩЕНИИ ГАЗА ОТ СЕЧЕНИЯ 1 -1 ДО СЕЧЕНИЯ 2 -2 СКОРОСТЬ ГАЗА ВОЗРАСТЕТ , А ДАВЛЕНИЕ И ТЕМПЕРАТУРА УМЕНЬШАТСЯ. При 1 2 движении газа в канале к нему подводится тепло от окружающей среды и отводится работа внешнему потребителю.

Работа, совершаемая 1 килограммом газа на участке 1 -2 затрачивается на: Изменение кинетической энергии Изменение потенциальной энергии Работу, отдаваемую внешнему потребителю Работу проталкивания Работу сил трения

Тогда 1 -ый закон для потока запишется: Вся работа сил трения преобразуется в теплоту трения, то есть , а , тогда в окончательном виде 1 -ый закон для потока будет иметь вид: (1)

Или с учетом теплоты трения (1 -а) Обобщенное уравнение Бернулли Запишем 1 -ый закон в дифференциальной форме, с учетом соотношения

Перепишем это выражение с учетом, того что (2) (2 -а) Уравнения (2) и (2 -а) называют обобщенным уравнениями Бернулли в дифференциальной и интегральной формах.

Истечение газа из суживающегося сопла Рассмотрим течение газа по суживающему каналу (соплу) при допущениях: Течение без трения Изменение потенциальной энергии мало Течение энергоизолированно Из (1 -2) следует (3) Увеличение скорости газа в сопле происходит за счет уменьшения энтальпии.

Введем понятие параметров торможения, под которыми будем понимать параметры обратимо заторможенного газа. (с=0) -энтальпия заторможенного потока -давление заторможенного потока -температура торможения Тогда выражение (3) примет вид (4)

Из уравнения Бернулли для рассматриваемого случая следует или после интегрирования (5) При истечении идеального газа располагаемая работа вычисляется А выражение для скорости истечения примет вид (5 а)

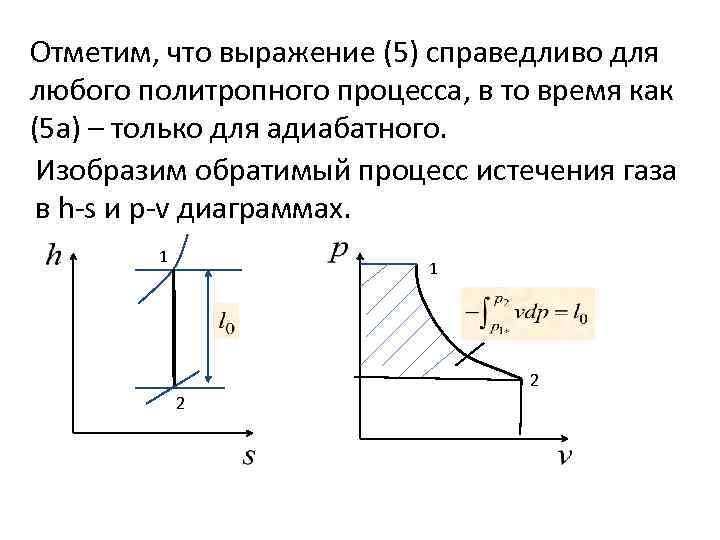Отметим, что выражение (5) справедливо для любого политропного процесса, в то время как (5 а) – только для адиабатного. Изобразим обратимый процесс истечения газа в h-s и p-v диаграммах. 1 1 2 2

Как следует из формулы (5 -а) скорость газа на выходе из сопла зависит от физических свойств, отношения давлений и начальных параметров газа перед соплом. Расход газа через суживающееся сопло. Объём газа, проходящий за 1 с. через выходное сечение сопла определится , массовый же расход будет равен. Поскольку расход газа вдоль сопла неизменен эта формула будет справедлива для любого сечения сопла

В изоэнтропном процессе изменения давления связаны с изменением объёма соотношением , откуда Расход газа с учетом (5 -а) выразится (6)

(6 -а) Заметим, что расход обращается в 0 при и Первый случай соответствует отсутствию движущих сил и, поэтому скорость потока равна 0. Второйтребует дополнительного исследования. Найдем максимум функции (6 -а) или (7) Давление, при котором расход достигает максимума называют критическим, а параметры

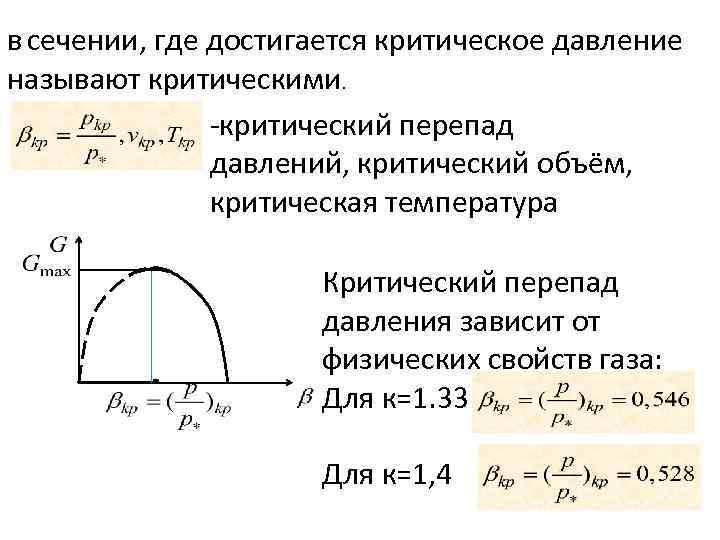в сечении, где достигается критическое давление называют критическими. -критический перепад давлений, критический объём, критическая температура Критический перепад давления зависит от физических свойств газа: Для к=1. 33 Для к=1, 4

Левая ветвь кривой в суживающемся сопле не реализуется. Расход , достигнув наибольшего значения, сохраняется вплоть до давления за соплом равным нулю. В 1839 году Сен-Венан выдвинул гипотезу, что на срезе суживающегося сопла получить давление меньшее критического невозможно. Следовательно, при любых, сколь угодно малых давлениях в окружающей среде, на срезе суживающегося сопла сохраняется давление равное критическому. Вычислим скорость газа при максимальном расходе его через сопло.

Для этого в (5 -а) подставим критический перепад давлений Итак, на выходе из суживающегося сопла максимальная скорость истечения составит

Скорость звука. Скоростью звука называют скорость распространения малых возмущений в упругой среде. Она определяется по формуле Эта формула позволяет определять скорость звука в газах, жидкостях и твердых телах. Так, при давлении 1 бар и температуре 20 С скорость звука в водяном паре 471 метр в секунду в воде-1505, а в железе 5130 м/с. Для идеального газа , то есть зависит от физических свойств газа и пропорциональна

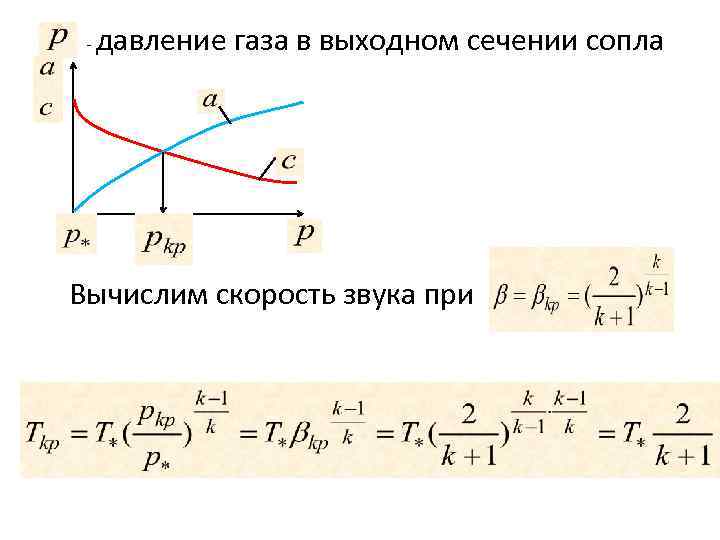- давление газа в выходном сечении сопла Вычислим скорость звука при

Тогда скорость звука в критическом сечении определится Итак, в критическом сечении скорость истечения равна скорости звука, а давление газа становится неизменным и равным критическому, так как возмущения давления окружающей среды , движущиеся со скоростью звука не достигают выходного сечения сопла.

Адиабатное течение с трением. Рассмотрим истечение газа из суживающих каналов при наличии трения. В этом случае часть кинетической энергии движущегося газа превращается в работу трения, а последняя в теплоту. Процесс становится необратимым, энтропия потока возрастает. Изобразим процесс необратимого течения в и и диаграммах.

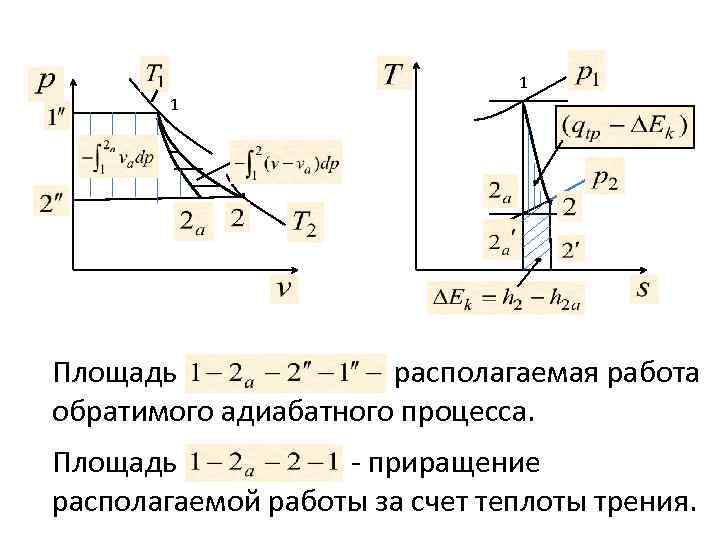1 1 Площадь располагаемая работа обратимого адиабатного процесса. Площадь - приращение располагаемой работы за счет теплоты трения.

Площадь потеря кинетической энергии при движении с трением. Как следует из диаграммы: (0) Потеря кинетической энергии снижает скорость газа на выходе из сопла ( группы сопел), так что действительная скорость будет меньше теоретической (скорости истечения в обратимом адиабатном процессе) Отношение действительной скорости истечения к теоретической называют коэффициентом сохранения скорости.

-коэффициент сохранения скорости, тогда потеря кинетической энергии выразится (1) зависит от многих факторов и для гладких плавно суживающихся каналов его величина составляет 0, 98 -0, 95. При анализе процессов течения с трением вводится понятие коэффициента потерь, который определяется отношением потери кинетической энергии к теоретической

(2) Коэффициент же полезного действия преобразования тепловой энергии в кинетическую будет определяться отношением действительной кинетической энергии к теоретической, которую можно получить при истечении без потерь. (3)

Определенный, таким образом , КПД учитывает только потери в соплах. Как следует из (0) потери кинетической энергии составляют только часть теплоты трения. Остальная часть превращается вновь в кинетическую энергию, как бы компенсируя частично её потери. » Возврат» кинетической энергии количественно учитывается коэффициентом возврата тепла, под которым понимается отношение «возвращенного тепла» к располагаемой работе процесса.

Из 1 -го закона термодинамики для обратимого истечения ( течения без потерь) следует При течении с потерями, поскольку внешнего подвода тепла нет, выражение 1 -го закона запишется Сравнивая их Получим диаграмме это площадь В

Методы анализа эффективности циклов Теплосиловые циклы подразделяются на 3 группы: теплосиловые газовые; теплосиловые паровые и циклы прямого преобразования теплоты в работу. В первых рабочим телом является газ, во вторыхпары жидкостей. В циклах прямого преобразования нет турбины, то есть отсутствует звено преобразования тепловой в механическую энергию.

При оценке эффективности теплосиловой установки следует получить ответы на 2 вопроса: 1. Насколько велик КПД обратимого цикла, от каких факторов он зависит и что надо сделать для его увеличения? 2. Насколько велики необратимые потери в реальном цикле; как распределяются они по отдельным элементам установки и , следовательно, какие из них необходимо усовершенствовать для снижения необратимости.

Условимся в дальнейшем термин « термический КПД» применять для анализа эффективности обратимых циклов , а « внутренний КПД» для анализа действительных циклов. -термический КПД обратимого цикла - работа обратимого цикла - подведенное в цикле тепло

- внутренний абсолютный КПД цикла - действительная работа цикла (с учетом потерь на трение и др. ) Введем понятие внутреннего относительного КПД

-внутренний относительный КПД цикла. Он показывает насколько совершенен действительный цикл по сравнению с обратимым. Помимо потерь, обусловленных движением рабочего тела (трение) существуют другие потери: трение в подшипниках, потери в электрогенераторе и другие виды потерь. Они учитываются эффективным КПД - эффективный КПД цикла. - работа, отданная внешнему потребителю.

Методы сравнения эффективности обратимых циклов. 1. Коэффициент заполнения цикла равен отношению работы произвольного обратимого цикла к работе, полученной в цикле Карно, осуществленном в том же интервале температур, что и сравниваемый цикл. Чем больше коэффициент заполнения, тем эффективнее обратимый цикл.

2. По средним температурам подвода и отвода тепла. Вывод: Чем выше средняя температура подвода теплоты в цикле , тем выше наоборот, чем ниже , тем выше и,

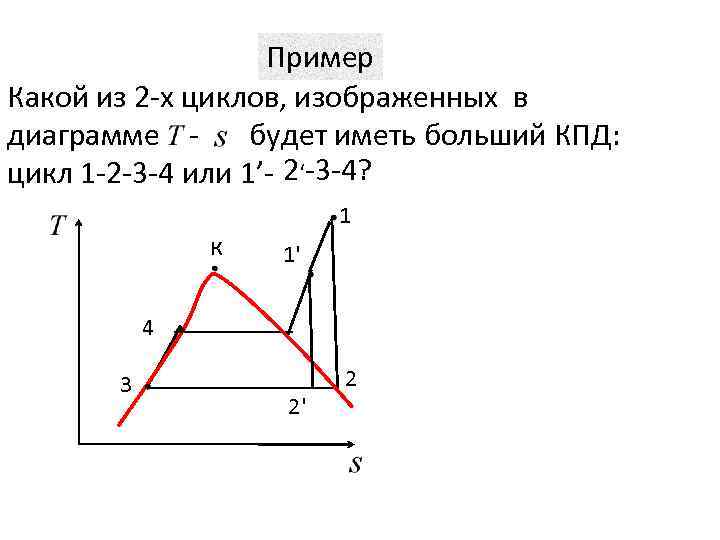Пример Какой из 2 -х циклов, изображенных в диаграмме будет иметь больший КПД: цикл 1 -2 -3 -4 или 1’- 2‘-3 -4? к 1 1' 4 3 2' 2

Методы анализа эффективности необратимых циклов. 1. Метод коэффициентов полезного действия. Обязательным элементом любого теплосилового цикла являются устройства расширения и сжатия рабочего тела. В циклах ПТУ и ГТУ это турбина и компрессор (насос), в циклах ДВС – поршень и цилиндр. Реальные процессы расширения и сжатия всегда сопровождаются трением рабочего тела со стенками каналов и между отдельными струйками. Это приводит к росту энтропии и потере работоспособности рабочего тела.

Степень совершенства устройств расширения характеризуется их КПД, представляющим отношение действительной работы к теоретической, получаемой при расширении без потерь. -КПД турбины - действительная работа турбины в процессе - теоретическая работа расширения

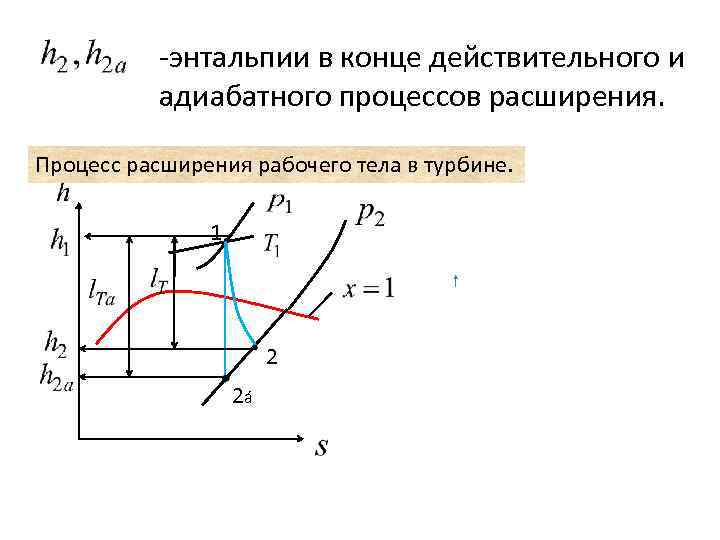-энтальпии в конце действительного и адиабатного процессов расширения. Процесс расширения рабочего тела в турбине. 1 2 2á

В устройствах сжатия действительная работа больше теоретической и поэтому их КПД определяется отношением теоретической работы к действительной. -КПД компрессора -энтальпии рабочего тела на выходе и входе в компрессор. -энтальпия в обратимом процессе сжатия.

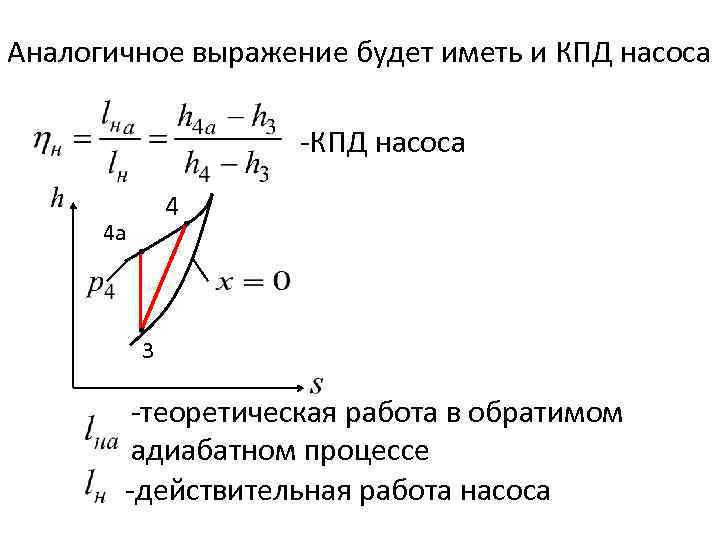Аналогичное выражение будет иметь и КПД насоса -КПД насоса 4 4 a 3 -теоретическая работа в обратимом адиабатном процессе -действительная работа насоса

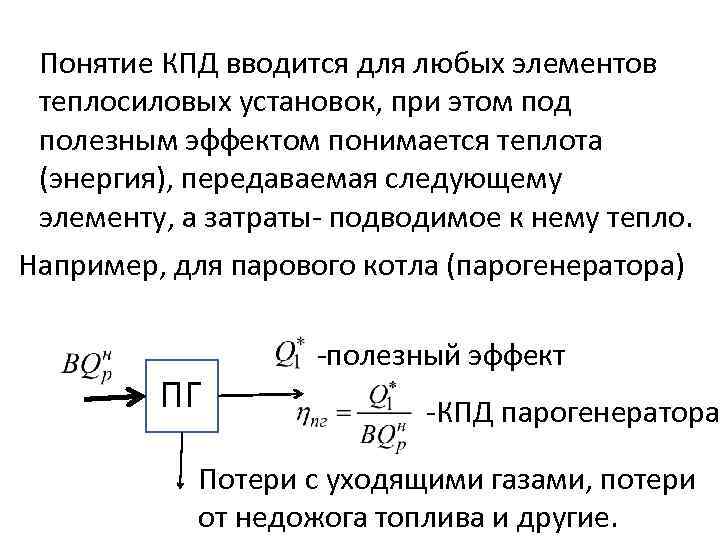Понятие КПД вводится для любых элементов теплосиловых установок, при этом под полезным эффектом понимается теплота (энергия), передаваемая следующему элементу, а затраты- подводимое к нему тепло. Например, для парового котла (парогенератора) ПГ -полезный эффект -КПД парогенератора Потери с уходящими газами, потери от недожога топлива и другие.

Рассмотрим метод оценки эффективности с помощью КПД на примере цикла паросиловой установки. Выделим основные этапы превращения и передачи энергии в этом цикле: -сжигание топлива и передача выделившегося тепла рабочему телу (процессы в ПГ) -транспортирование рабочего тела (пара) от ПГ к турбине. (процесс в главном паропроводе) -превращение тепла в механическую работу в ПТУ -затраты механической энергии на трение в подшипниках, привод вспомогательных механизмов и другие потери.

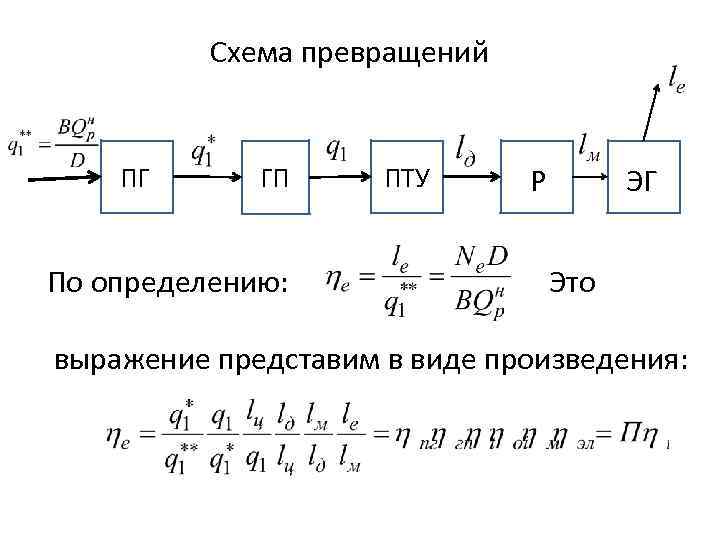Схема превращений ПГ ГП По определению: ПТУ Р ЭГ Это выражение представим в виде произведения:

Оценим КПД современной ТЭС по наиболее достижимым КПД элементов: КПД парогенератора – 0, 9 КПД главного паропровода – 0, 99 Термический КПД цикла – 0, 55 Внутренний относительный КПД цикла – 0, 85 Механический КПД – 0, 99 КПД электрического генератора -0, 99 Тогда электрический КПД будет равен

Самые большие потери энергии в виде потерь тепла наблюдаются в паротурбинной установке (ПТУ). Здесь отводится теплота от рабочего тела и передается окружающей среде. По методу КПД самым несовершенным элементом является ПТУ и , казалось бы, его и надо совершенствовать. Однако и КПД турбины и совершенство конденсатора довольно высоки, поэтому достичь заметного повышения КПД всей установки за счет их усовершенствования не удается. Надо искать другие направления совершенствования?

Энтропийный метод оценки эффективности необратимых циклов В основе этого метода лежит теорема Луи – Стодола: уменьшение работоспособности системы равно произведению температуры окружающей среды на приращение энтропии системы или Таким образом, вычислив потери работоспособности в отдельных элементах, можно определить самый несовершенный из них.

Условно все потери в циклах подразделяются на 2 группы: -потери от внешней необратимости, вызванные наличием конечной разности температур в процессе перехода тепла от одного элемента другому; - потери от внутренней необратимости, обусловленной наличием трения и потерь тепла из-за теплообмена с окружающей средой.

Обратимый цикл ПТУ (цикл Ренкина)