ПРЕЗЕНТАЦИЯ К ЗАЩИТЕ КУРСОВОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ «ИНФОРМАТИКА» Выполнил студент гр. 3130 Садыков И. И.
Решение СДУ модифицированным методом Эйлера
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ 1. Составить программу для решения с заданной точностью системы дифференциальных уравнений модифицированным методом Эйлера; 2. Отладить программу на контрольном примере. Выбрать шаг интегрирования; 3. Оценить погрешности вычислений; 4. Заключение
РЕШЕНИЕ СДУ МОДИФИЦИРОВАННЫМ МЕТОДОМ ЭЙЛЕРА Модифицированный метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое).
МЕТОД РЕШЕНИЯ Рассмотрим дифференциальное уравнение (1) y/=f(x, y) с начальным условием y(x 0)=y 0. Разобьем наш участок интегрирования на n равных частей. На малом участке интегральную кривую заменим прямой линией. Получаем точку Мк(хк, ук). Через Мк проводим касательную: у=ук=f(xk, yk)(x-xk) Делим отрезок (хк, хк 1) пополам x. Nk/=xk+h/2=xk+1/2 y. Nk/=yk+f(xk, yk)h/2=yk+yk+1/2 Получаем точку Nk/. В этой точке строим следующую касательную: y(xk+1/2)=f(xk+1/2, yk+1/2)=αk Из точки Мк проводим прямую с угловым коэффициентом αк и определяем точку пересечения этой прямой с прямой Хк 1. Получаем точку Мк/. В качестве ук+1 принимаем ординату точки Мк/. Тогда: ук+1=ук+αкh xk+1=xk+h αk=f(xk+h/2, yk+f(xk, Yk)h/2) yk=yk-1+f(xk-1, yk-1)h
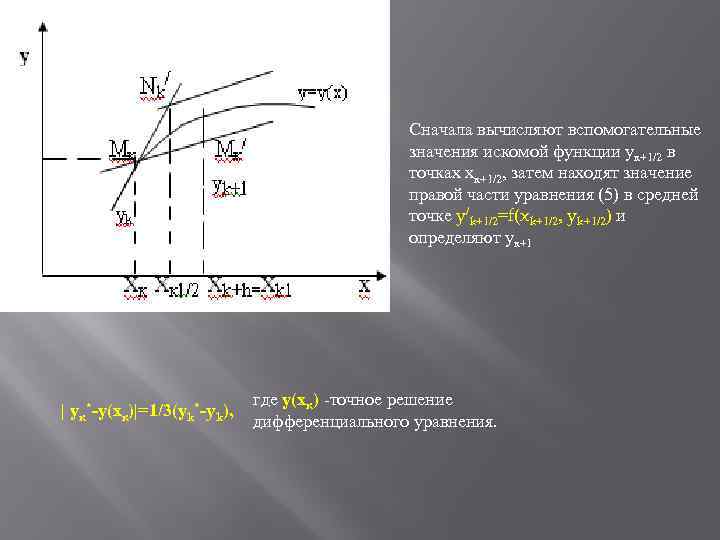
Сначала вычисляют вспомогательные значения искомой функции ук+1/2 в точках хк+1/2, затем находят значение правой части уравнения (5) в средней точке y/k+1/2=f(xk+1/2, yk+1/2) и определяют ук+1 | ук*-у(хк)|=1/3(yk*-yk), где у(хк) -точное решение дифференциального уравнения.
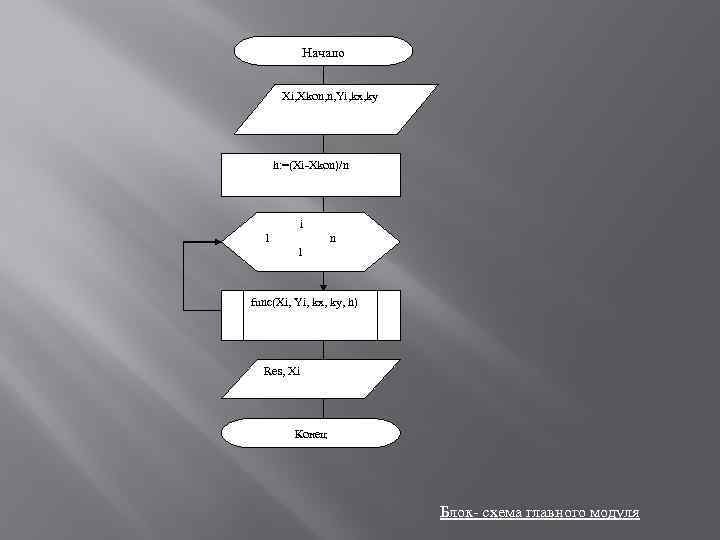
Начало Xi, Xkon, n, Yi, kx, ky h: =(Xi-Xkon)/n i 1 n 1 func(Xi, Yi, kx, ky, h) Res, Xi Конец Блок- схема главного модуля
![Интерфейс программы Программа запрашивает начальные и конечные значения [a; b], число шагов, коэфициенты при](https://present5.com/presentation/182812413_180179172/image-9.jpg "Интерфейс программы Программа запрашивает начальные и конечные значения [a; b], число шагов, коэфициенты при")
Интерфейс программы Программа запрашивает начальные и конечные значения [a; b], число шагов, коэфициенты при x и y и нач значение y
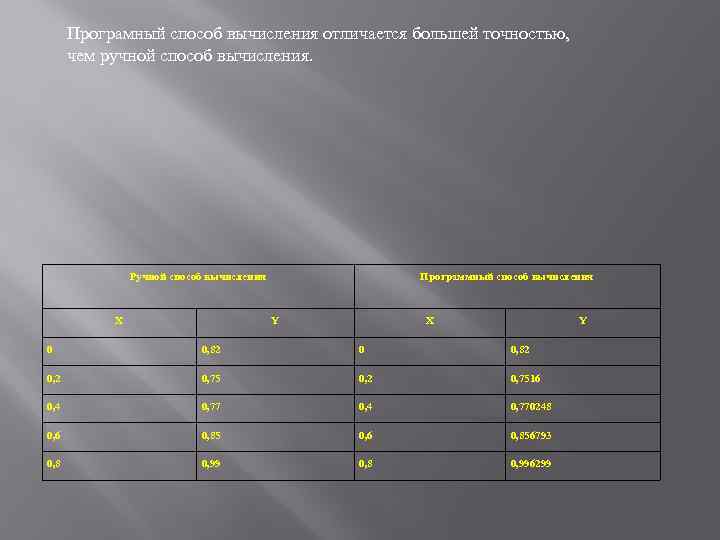
Програмный способ вычисления отличается большей точностью, чем ручной способ вычисления. Ручной способ вычисления Х Программный способ вычисления Y X Y 0 0, 82 0, 7516 0, 4 0, 770248 0, 6 0, 856793 0, 8 0, 996299
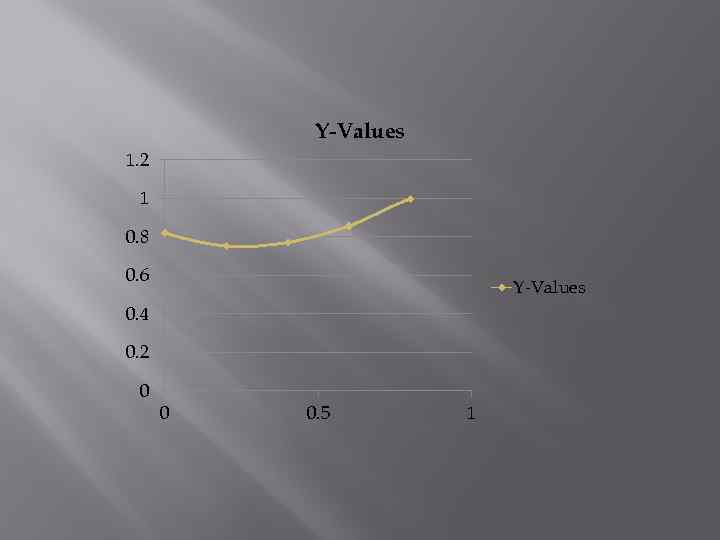
Y-Values 1. 2 1 0. 8 0. 6 Y-Values 0. 4 0. 2 0 0 0. 5 1
Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать дифференциальные уравнения по модифицированному методу Эйлера, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Данная программа решает заданную пользователем дифференциальное уравнение за минимальный промежуток времени. При этом пользователю предоставляется возможность визуально оценить решение, рассматривая график полученного решения. К достоинствам программы можно отнести также удобный пользовательский интерфейс, возможность ввода пользовательских дифференциальных уравнений, а также давольно высокая стабильность работы.
Скачать презентацию К ЗАЩИТЕ КУРСОВОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ ИНФОРМАТИКА
презентация к курсовой.pptx