Презентация file 20080804121343

МОУ «Высокоярская сош» Бакчарского района Томской области Теорема Пифагора: вне урока. Выполнила: Суханова Ольга, 8 класс Руководитель: Беляева Татьяна Васильевна, учитель физики и математики

Цели и задачи: Кто на самом деле открыл теорему? Почему она долгое время называлась «теоремой невесты» ? Почему «пифагоровы штаны во все стороны равны» ? Существуют ли другие доказательства теоремы? Как используется теорема Пифагора в решении задач; в искусстве? Поиск исторических задач на теорему Пифагора

Из истории теоремы Пифагора Древний Китай Математическая книга Чу-пей: «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4».

Теорема Пифагора у древних египтян Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э. , во времена царя Аменемхета (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты , или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Теорема в Вавилонии «Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку. «

У индусов Геометрия у индусов , как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.

«Пифагоровы штаны во все стороны равны»

В течение двух тысячелетий наиболее распространенным доказательством теоремы Пифагора было придуманное Евклидом. Оно помещено в его знаменитой книге «Начала» . Евклид опускал высоту СН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах. Чертёж, применяемый при доказательстве этой теоремы, в шутку называют «пифагоровы штаны» . В течение долгого времени он считался одним из символов математической науки.

Рисунки учащихся средних веков

ПРОСТЕЙШИЕ ДОКАЗАТЕЛЬСТВА Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для треугольника ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по два

Доказательство 9 века н. э. На рисунке квадраты, построенные на катетах, размещены ступенями один рядом с другим. Эту фигуру, которая встречается в доказательствах, датируемых не позднее, чем 9 столетием н. э. , индусы называли «стулом невесты».

Доказательство Перигаля. В учебниках нередко встречается разложение указанное на рисунке (так называемое «колесо с лопастями»; это доказательство нашел Перигаль ). Через центр O квадрата, построенного на большем катете, проводим прямые, параллельную и перпендикулярную гипотенузе. Соответствие частей фигуры хорошо видно из чертежа

Применение Теоремы Пифагора Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом, d 2 =2 a 2 , откуда : d= а √ 2. Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b²

Высота равностороннего треугольника Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом имеем a 2=h 2+(a/2)2, или h 2=(3/4)a 2. Отсюда вытекает h=1/2 а √ 3.

На рисунке изображен куб , внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна а √ 2. Отсюда имеем d 2=a 2+2 a 2, d 2=3 a 2, d=a√ 3.

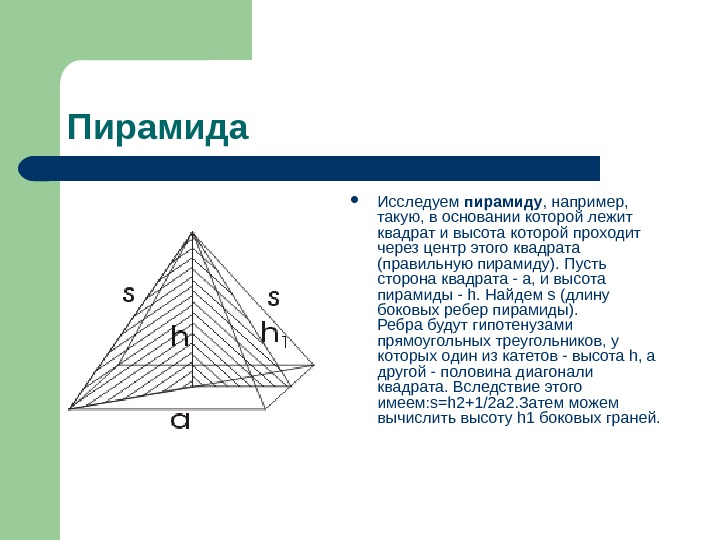
Пирамида Исследуем пирамиду , например, такую, в основании которой лежит квадрат и высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть сторона квадрата — а, и высота пирамиды — h. Найдем s (длину боковых ребер пирамиды). Ребра будут гипотенузами прямоугольных треугольников, у которых один из катетов — высота h, а другой — половина диагонали квадрата. Вследствие этого имеем: s=h 2+1/2 a 2. Затем можем вычислить высоту h 1 боковых граней.

Готические и Романские стили

Послание марсианам в виде теоремы Пифагора

Задача индийского математика XII века Бхаскары «На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота? «

Задача из китайской «Математики в девяти книгах» «Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша? «

Задача из учебника «Арифметика» Леонтия Магницкого «Случится некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обретете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать»

ПИФАГОРОВА ГОЛОВОЛОМКА

Учебное исследование по теме «Теорема Пифагора» Задача. Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?