Презентация 5 ДЕ Оптика готовый

ОПТИКА ( 5 дидактическая единица )

ВОЛНОВАЯ ОПТИКА 1. Интерференция света Условия наблюдения интерференции: волны монохроматические λ 1 = λ 2 ν 1 = ν 2 разность фаз постоянна колебания светового вектора происходят в одном направлении Интерференция света – сложение двух или нескольких когерентных волн, в результате которого происходит перераспределение световой энергии в пространстве. волны одинаковой частоты:

λ 1 ≠ λ 2 ν 1 ≠ ν 2 волны не когерентны

ΔΔ 2– связь разности фаз с оптической разностью хода Условия минимума при интерференции: . . . 2, 1, 0, m m 2Δ )12(Δ m волны складываются в противофазе волны складываются в одной фазедля разности фаз: Условия максимума при интерференции: для опт. разности хода: mдля разности фаз: для опт. разности хода: 2 )12( m

)12(Δ m 2 )12( m min : kxt. Atxcos), ( начальная фаза колебаний фаза волны Δ 2 Δ 4 2 Δ

Как отличаются оптические разности хода лучей: для соседних темных интерференционных полос? для соседних светлых интерференционных полос? для соседних темной и светлой интерференционной полосы? mΔ max m =2 =800 нмΔ =2 λ Δ = λ /2min 2 )12(Δ m

В т. А приходят волны от двух когерентных источников S 1 и S 2. Длина волны в вакууме 600 нм. При какой минимальной разности фаз в т. А будет наблюдаться минимум интерференции? m = 0 mΔ max min )12(Δ m min 2 )12(Δ m. Укажите, при каких из перечисленных ниже значениях разности хода в т. А будет наблюдаться максимум ( минимум )интерференции: 0; 300 нм; 600 нм; 900 нм; 1200 нм; 1500 нм; 3000 нм minΔ

+ λ /2 1 2 отражается от оптически менее плотной средылуч 1 : При отражении волны от оптически более плотной среды появляется дополнительная разность хода λ /2отражается от оптически более плотной средылуч 2 : Δ = 2 dn — 0оптический путь 2 луча оптический путь 1 луча

mΔmax d 1 ׳׳ 1 Δ↓d ↓ λ ↓Δ ~ d Δ ~ n Δ ~ α 220 22 /sinnd

Δ↓ n ↓ λ ↓ 220 22 /sinnd

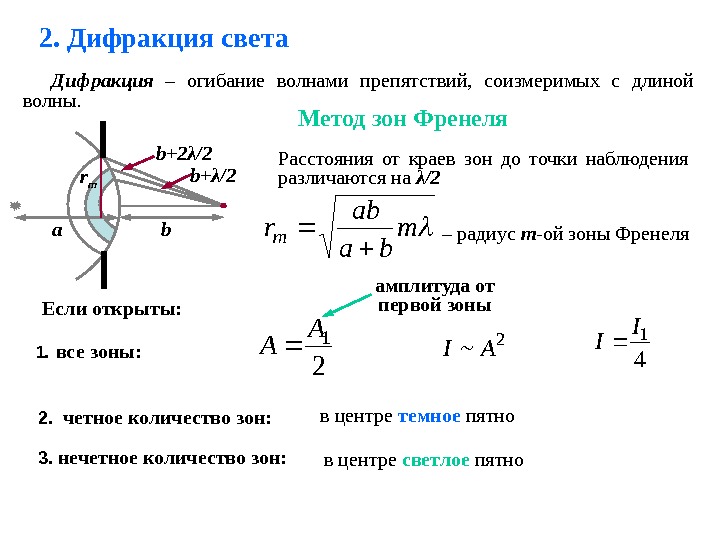
2. Дифракция света Метод зон Френеля. Дифракция – огибание волнами препятствий, соизмеримых с длиной волны. Расстояния от краев зон до точки наблюдения различаются на λ /2 m ba ab r m – радиус m -ой зоны Френеляb b+ λ /2b+2 λ /2 а r m 2 1A A 4 1I I 2 A~IЕсли открыты: в центре темное пятно в центре светлое пятно 3. нечетное количество зон: 2. четное количество зон: 1. все зоны: амплитуда от первой зоны

2 1A A 4 1I I На рисунке представлена схема разбиения волновой поверхности Ф на зоны Френеля. Разность хода между лучами N 1 P и N 2 P равна… Δ = λ /2 2 A~I Расстояния от краев зон до точки наблюдения различаются на λ /

m ba ab r m а = ∞ bmrlim m a b r m m 2 62 3 105.

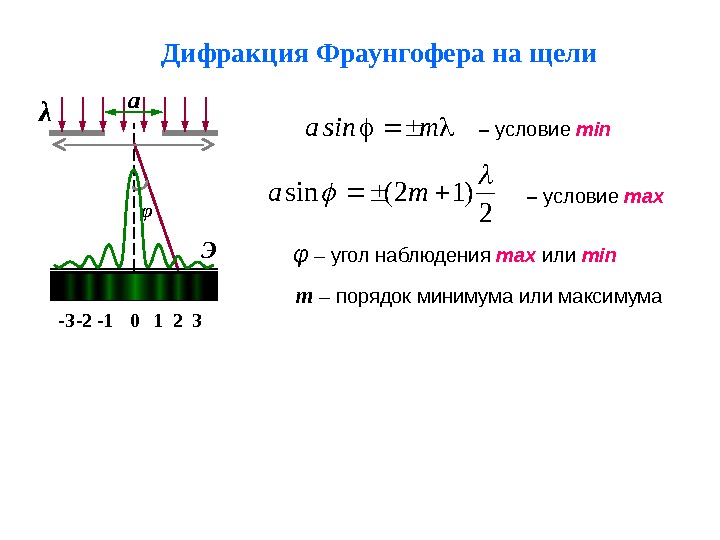
Дифракция Фраунгофера на щели φ 0 1 2-1-2-3 3 msina – условие min 2)12(sin ma – условие max m – порядок минимума или максимума. Эa λ φ – угол наблюдения max или min

Дифракция Фраунгофера на решетке λ Эd φ md sin – условие главных max 0 1 2-1-2 λ =const расстояние между max ↑d ↓ sin φ ↑ d =const λ ↑ sin φ ↑ λ кр > λ зел φ кр > φ зел

md sinmax : λ кр > λ фиол φ кр > φ фиол (сильнее отклоняются красные лучи)

Имеются 4 решетки с различными постоянными d, освещаемые одним и тем же монохроматическим излучением различной интенсивности. Какой рисунок иллюстрирует положение главных максимумов, создаваемых дифракционной решеткой с наименьшей постоянной решетки ? md sinmax : m = const λ = const чем меньше d , тем больше sin φ√

Одна и та же дифракционная решетка освещается различными монохроматическими излучениями с разными интенсивностями. Какой рисунок соответствует случаю освещения светом с наименьшей длиной волны? md sin max : m = const d = const чем меньше λ , тем меньше sin φ√с наибольшей частотой? V ч ем больше ν , т ем меньше λ

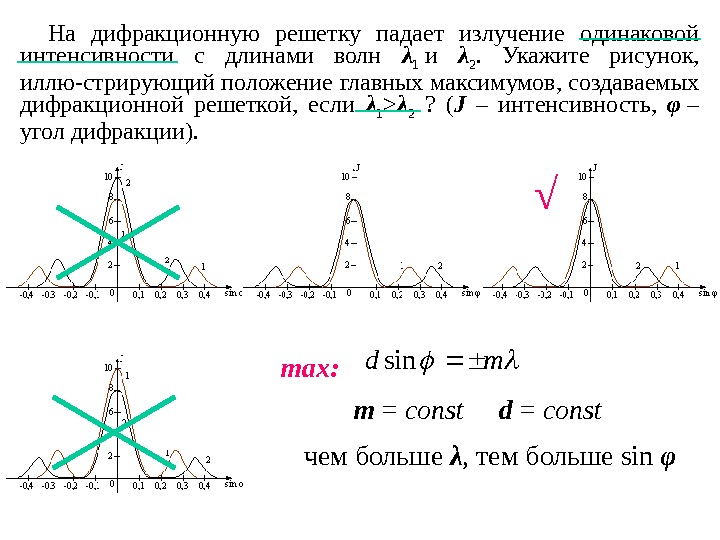
На дифракционную решетку падает излучение одинаковой интенсивности с длинами волн λ 1 и λ 2. Укажите рисунок, иллю-стрирующий положение главных максимумов, создаваемых дифракционной решеткой, если λ 1 > λ 2 ? ( J – интенсивность, φ – угол дифракции). md sin max : m = const d = const чем бол ьше λ , тем больше sin φ√

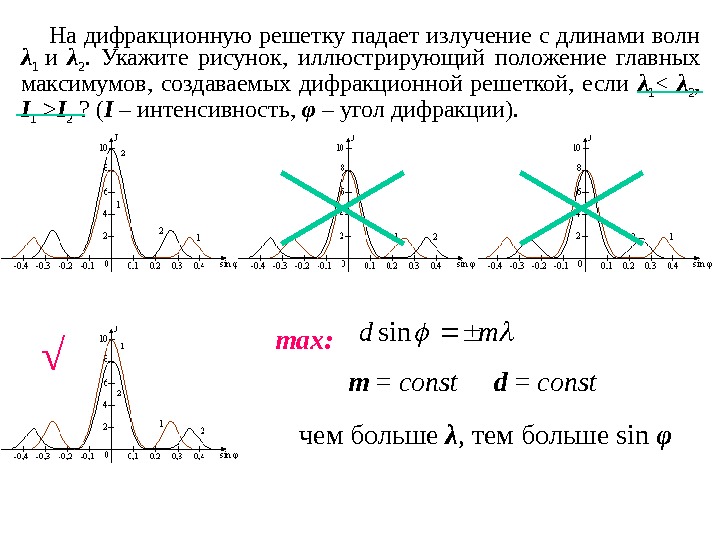
На дифракционную решетку падает излучение с длинами волн λ 1 и λ 2. Укажите рисунок, иллюстрирующий положение главных максимумов, создаваемых дифракционной решеткой, если λ 1 I 2 ? ( I – интенсивность, φ – угол дифракции). md sin max : m = const d = const чем бол ьше λ , тем больше sin φ√

N 2 > N 1При увеличении числа щелей в решетке максимумы становятся более узкими и яркими. Положения максимумов не изменяется md sin max : d 2 = d

4. Поляризация Естественный – свет со всевозможными равновероятными ориентациями вектора ЕE Плоскополяризованный – свет, в котором вектор Е колеблется только в одной плоскости (в плоскости поляризации) E Поляризаторы: пластинка турмалина, призма Николя, поляроид.

– с тепень поляризацииminmax II II P I 1 = I ест /2 I 1 I 2 min = 0 I 2 max = I 1 Чем больше разность между I max и I min , тем больше степень поляризации. 0P – естеств. свет 1P – поляриз. свет. I ест I 2 I ест – интенсивность естественного света I 1 — интенсивность поляризованного света, падающего на анализатор I 2 — интенсивность на выходе из анализатора – закон Малюса 2 12cos. II φ — угол между главной плоскостью анализатора и плоскостью поляризации падающего на него света

На пути естественного света помещены две пластинки турмалина. После прохождения пластинки 1 свет полностью поляризован. Если I 1 и I 2 – интенсивности света, прошедшего пластинки 1 и 2 соответственно, и I 2 = I 1 /4 , тогда угол между направлениями OO и O ΄ равен… Закон Малюса: 2 12cos. II 2 1 2cos I I 4 1 2 1 cos

J 1 J 2J 0 2 12cos. II 2 0 1 I I 20 2 2 cos I I 2 2 0 2 cos I I

P c > P b > P a. Чем больше разность между I max и I min , тем больше степень поляризации.

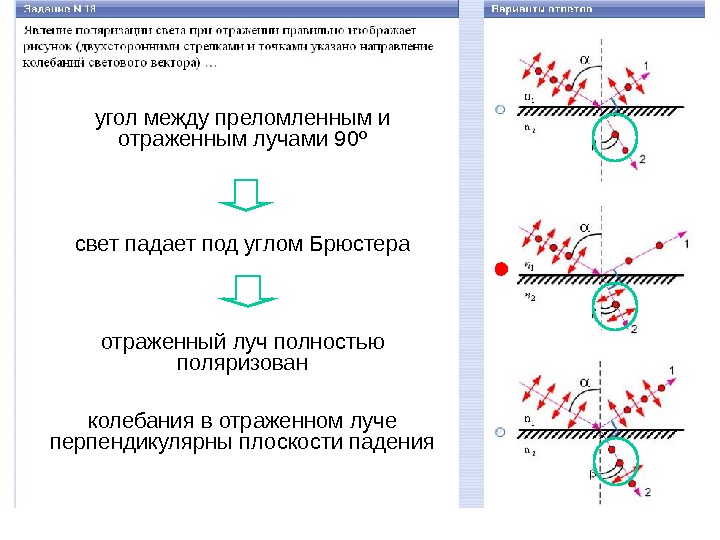
Поляризация при отражении и преломлении При многократном пре-ломлении степень поля-ризации увеличивается. 21 1 2tgn n n Бр – закон Брюстера полностью поляризован частично поляризованугол равен 90 ºВ отраженном луче преобладают колебания, перпендикулярные плоскости падения (на схеме больше точек); В преломленном луче – колебания параллельные плоскости падения (на схеме больше стрелок).

O O΄ 02J

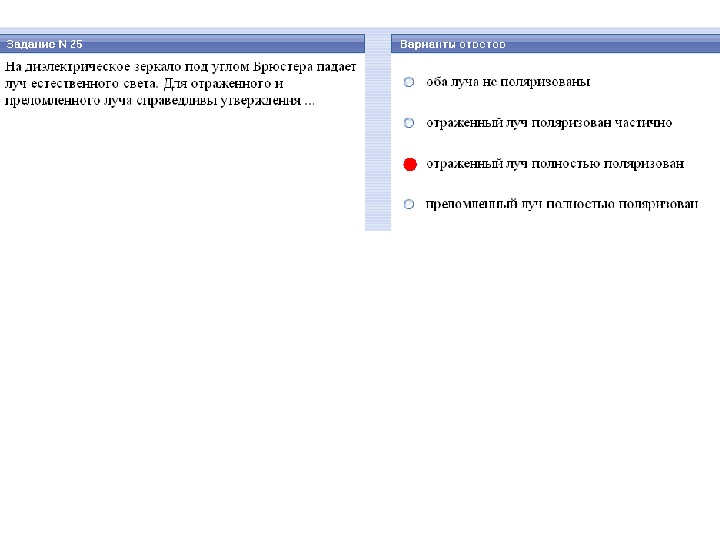
угол между преломленным и отраженным лучами 90 º свет падает под углом Брюстера отраженный луч полностью поляризован колебания в отраженном луче перпендикулярны плоскости падения

α =60ºβ =30ºα = α Бр tg α Бр = n 3n 30º 90º 60º α = α Бр α =60º β =180º-6 0º -9 0º β =30º

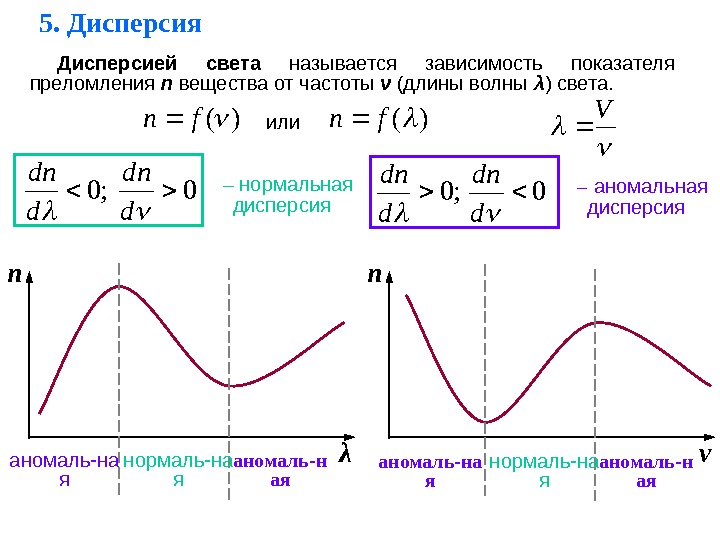
5. Дисперсия Дисперсией света называется зависимость показателя преломления n вещества от частоты ν (длины волны λ ) света. )(fn или ; 0 d nd – нормальная дисперсия V ; 0 d nd – аномальная дисперсия n λ аномаль-н аяаномаль-на я нормаль-на я n ν аномаль-н аяаномаль-на я нормаль-на я

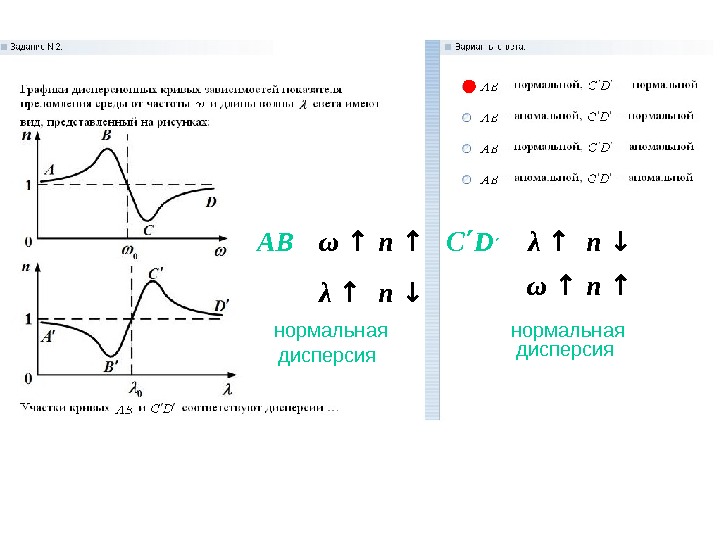
AB C ΄ D ΄ω ↑ n ↑ λ ↑ n ↓ нормальная дисперсия λ ↑ n ↓ ω ↑ n ↑ нормальная дисперсия

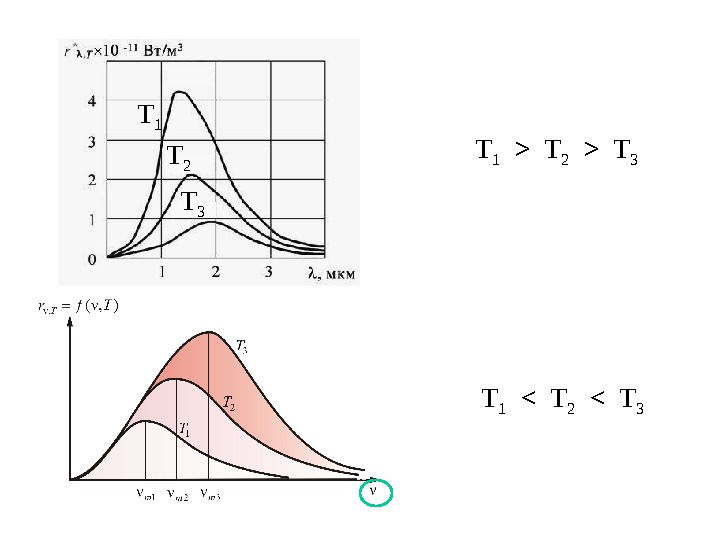
Длина волны (мкм)Интенсивность излученияr λ КВАНТОВАЯ ОПТИКА 1. Тепловое излучение Все тела, имеющие отличную от нуля абсолютную температуру – источники теплового излучения. d. Sdt d. W RT – энергетическая светимость 4 TR – закон Стефана-Больцман а На графике r λ ( λ ) R T – площадь под кривой при ↑ T площадь ↑ Tb/ max – закон Вина dd. R r T – спектральная плотность энергетической светимости λ max – длина волны, на которую приходится максимум функции r λ ( λ ) при ↑ T , λ max ↓

T 1 T 2 T 3>> T 1 T 2 T 3<<

На рисунке показана кривая зависимости спектральной плотности энергетической светимости абсолютно черного тела от длины волны при T=6000K. Если температуру тела уменьшить в 4 раза, то длина волны, соответствующая максимуму излучения абсолютно черного тела, … Если температуру тела уменьшить в 2 раза, то энергетическая светимость абсолютно черного тела… • увеличится в 2 раза • уменьшится в 4 раза • увеличится в 4 раза • уменьшится в 2 раза. Варианты ответов: Tb/max b T T b 2 12max 1max 1 2 TT 41 • уменьшится в 16 раз • увеличится в 2 раза • уменьшится в 4 раза • увеличится в 16 раз. Варианты ответов: 1max 2max 4 4 TR 4 2 4 1 21 TT R R 4 21 T T 4 2 16 16 12 RR

На рисунке показаны кривые зависимости спектральной плотности энергетической светимости абсолютно черного тела от длины волны при разных температурах. Если длина волны, соответствующая максимуму излучения, уменьшилась в 4 раза, то температура абсолютно черного тела. . . Если кривая 2 соответствует спектру излучения абсолютно черного тела при температуре 1500 К, то кривая 1 соответствует температуре (в). . . • увеличилась в 4 раза • уменьшилась в 2 раза • уменьшилась в 4 раза • увеличилась в 2 раза Варианты ответов: • 1000 К • 3000 К • 6000 К • 750 КОтветы : Tb/max 1 2 2max 1max T T 2000 500 constb. Tmax constb. T 4 4 max 1 2 T T 1 2 4 1 T T 21 4 TT

Tb/max 1 2 2max 1max T T 4 1 21 4TT При сером излучении интенсивность лучей для каждой длины волны при любой температуре составляет неизменную долю от интенсивности излучения черного тела.

при ↑ T площадь ↑ при ↑ T , λ max ↓ λ max 2 < λ max

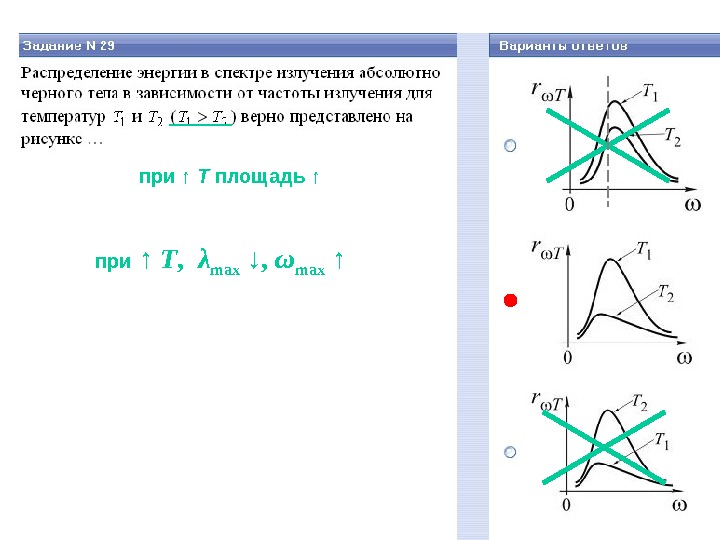
при ↑ T площадь ↑ при ↑ T , λ max ↓, ω max ↑

На рис. представлено распределение энергии в спектре абсолютно черного тела для двух температур: Т 1 (кривая 1) и Т 2. (кривая 2) Определите, как связаны температуры и энергетические светимости ( R T ) тел. На графике r λ ( λ ) R T – площадь под кривой R T 1 > R T 2 R T ~ T 4 T 1 > T 2 при ↑ T , λ max ↓ λ max 1 T

2. Фотоэффект Внешний фотоэффект – испускание электронов веществом под действием электромагнитного излучения. A m. V hmax 2 2 – уравнение Эйнштейнаh ν кинетическая э нергия электронаэ нергия фотона работа выхода электронов из металла (зависит только от свойств металла) h =6. 62 · 10 -34 Дж · с – постоянная Планка

h Aкр – красная граница фотоэффекта кр фотоэффекта нет кркр c энергии фотона недостаточно для выбивания электрона Ah m. V 2 2 max Для данного материала кинетическая энергия электрона зависит только от энергии падающего фотона (не зависит от их количества, т. е. интенсивности света)

J ~ N фот ~ I насинтенсивность света I нас ~ JI нас1 U з 1 I = I насвсе выбитые электроны достигли анода. Вольтамперная характеристика – зависимость силы фототока I от напряжения между катодом и анодом U. I нас3 = N электр 1 3 2 J 1 = J 2 J 3 = J 4 U з 2 4 > зk e. UE все выбитые электроны вернулись обратно. UI 0 задерживающие напряжениезаряд электрона

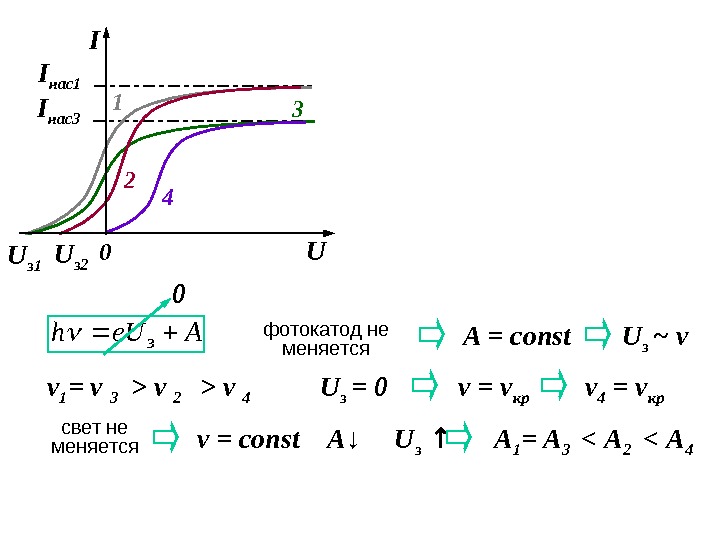
I нас1 U з 1 I нас3 1 3 2 U з 2 ν 1 = ν 3 > ν 24Ae. Uhз A = const U з ~ νфотокатод не меняется > ν 4 U з = 00 ν = ν кр свет не меняется ν = const U з ↑A ↓ ν 4 = ν кр A 1 = A 3 < A 2 < A 4UI

ν кр2ν кр1 A 2 > A 1νU з 0Ae. Uhз -A 2 / e-A 1 / e 21 U з ~ νν ν крαα A = const ; 11Ae. Uhз 22 1212зз. UUeh ν кр2 > ν кр 1 Δ Δз. U e h Ae. Uз tgconst ν = 0 Для всех металлов угол наклона зависимостей U з ( ν ) одинаков e h tg

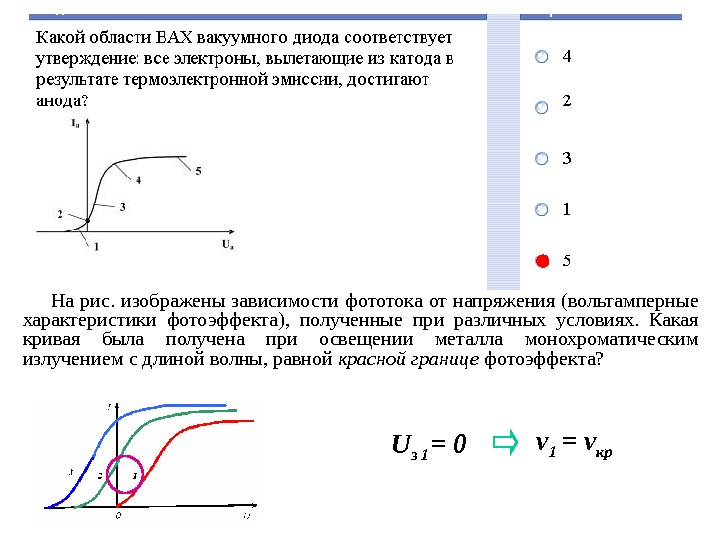
На рис. изображены зависимости фототока от напряжения (вольтамперные характеристики фотоэффекта), полученные при различных условиях. Какая кривая была получена при освещении металла монохроматическим излучением с длиной волны, равной красной границе фотоэффекта? U з 1 = 0 ν 1 = ν кр

I нас1 = I нас2 J 1 = J 2 U з 1 > U з 2 ν 1 > ν 2 I нас1 > I нас2 J 1 > J 2 U з 1 = U з 2 ν 1 = ν

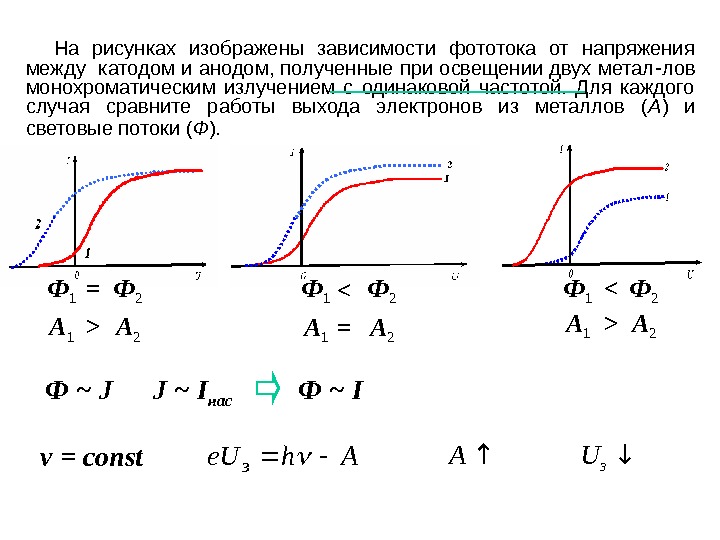
На рисунках изображены зависимости фототока от напряжения между катодом и анодом, полученные при освещении двух метал — лов монохроматическим излучением с одинаковой частотой. Для каждого случая сравните работы выхода электронов из металлов ( А ) и световые потоки ( Ф ). Ф 1 Ф 2 А 1 А 2> >< < == Ф ~ J J ~ I нас ν = const. Ahe. Uз A ↑ U з ↓Ф ~ I

На рисунке представлены две зависимости задерживающего напряжения U 3 от частоты падающего света ν для внешнего фотоэффекта. Укажите верные утверждения. А 2 λ 02 , где λ 01 и λ 02 – значения красной границы фотоэффекта для соответствующего металла Угол наклона зависимостей 1 и 2 одинаков ν кр2ν кр1 √Ah кр √√ ν кр2 > ν кр 1 λ кр2 A 1 ─ ─

На рисунке представлены две зависимости задерживающего напряжения U 3 от частоты падающего света ν для внешнего фотоэффекта. Укажите верные утверждения. А 2 > А 1 , где А 1 и А 2 – значения работы выхода электронов из соответ — ствующего металла С помощью этих зависимостей можно определить значение постоянной Планка Зависимости получены для двух различных металлов λ 01 < λ 02 , где λ 01 и λ 02 – значения красной границы фотоэффекта для соответствующего металла Угол наклона зависимостей 1 и 2 одинаков Зависимости получены для двух различных освещенностей одного металла зe. U m. V 22 max зk UE~ утверждения немного отличаются от предыдущих!

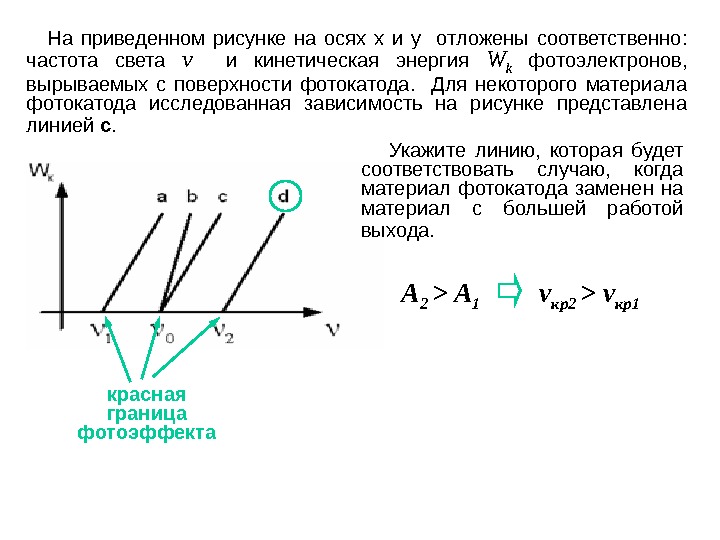
На приведенном рисунке на осях x и y отложены соответственно: частота света ν и кинетическая энергия W k фотоэлектронов, вырываемых с поверхности фотокатода. Для некоторого материала фотокатода исследованная зависимость на рисунке представлена линией с. Укажите линию, которая будет соответствовать случаю, когда материал фотокатода заменен на материал с большей работой выхода. ν кр2 > ν кр 1A 2 > A 1 красная граница фото э ффекта

J ~ N фот J ~ N электр= N электр

A m. V h 2 2 max

3. Свойства фотонов (квантов света) Энергиия: h. E c h h =6. 62 · 10 -34 Дж · с – постоянная Планка c =3 · 10 8 м/с – скорость света Масса: 2 mch. E 2 ch m Скорость: Импульс: mcp ch h

h pф A m. V hmax 2 2 c h h. Ecpф Ah m. V max 2 2 Acp m. V ф max

h pλ ↑ p ↓ λ инфр > λ вид > λ уф > λ рентг 21/4 1/2 4 h h p p

4. Давление света – давление, которое оказывает электромагнитное излучение, падающее на поверхность тела интенсивности света отражающей способности тела Зависит от: Обусловлено: импульсом , переданным поверхности падающими фотонами 2 cos)1(K c J P Давление при падении света под углом α к нормали: K – коэффициент отражения: J – интенсивность падающего света; c – скорость света ; K = 1 – зеркальное тело K = 0 – абсолютно черное тело Световое давление на абсолютно черное тело в два раза меньше, чем на зеркальное.

h p. Световое давление на черное тело меньше, чем на белое. Чем больше импульс падающих фотонов, тем большее давление они оказывают p ↑ λ ↓ Световое давление на черное тело меньше, чем на зеркальное.

J ~ N фот J 2 = J 1 / 2 K 2 = 0K 1 = 1 2 cos)1(K c J P P 2 = P 1 / 4 J 2 = J 1 K 2 = 0K 1 = 1 P 2 = P 1 /

– объёмная плотность энергии излученияw = J /c 2 cos)1(K c J P Параллельный пучок света падает по нормали на зачерненную плоскую поверхность, производя давление Р. При замене поверхности на зеркальную давление света не изменяется, если угол падения (отсчитываемый от нормали к поверхности) будет равен… Варианты ответов: • 45 º • 30 º • 60 ºK 1 = 0 α 1 = 0 P 1 = P K 2 = 1 P 2 = P α 2 = ? 2 2 1 2 cos 2 1 cos 2 2 2 1 cos

Параллельный пучок свет, падающий на зеркальную плоскую поверхность, под углом α =60° (отсчитываемым oт нормали к поверхности), производит давление Р. Если тот же пучок света направить по нормали на зачерненную поверхность, то световое давление будет равно. . . Варианты ответов: • Р/2 • 2Р • 4РK 1 = 1 α 1 = 6 0º P 1 = P K 2 = 0 P 2 = ? α 2 = 0 2 cos)1(K c J P 1 2 1cos 2 c J P 2 2 2cos c J P 1 2 2 2 1 2 cos P P 2 5.

5. Эффект Комптона – рассеяние фотонов электромагнитного излучения на свободных электронах. cos 1’Δe р ф – импульс фотона до столкновения; р е- – импульс электрона; р ф ΄ – импульс фотона после столкновения; φ – угол рассеяния фотона. – изменение длины волны падающего фотона. ЗСИ — eppp фф ЗСЭ Wh. Wh 0 энергия электрона до и после столкновения λ e =2, 426 пм φ ↑ Δ λ ↑ λ ΄ ↑ ν΄ ↓

фp ЗСИ — eppp фф φ -e p фp ? — ep cospp ф — e cos- e фp p 32 — e фp p

На рисунке показаны направления падающего фотона ( γ ), рассеянного фотона ( γ ‘) и электрона отдачи ( e ). Угол рассеяния 90°, направление движения электрона отдачи составляет с направлением падающего фотона угол φ =30 o. Если импульс падающего фотона Pф, то импульс рассеянного фотона равен… ЗСИ — eppp фф фp φ — ep фp ? ф p фpp tg ф 3ф фp p tgpp ф ф

На рисунке показаны направления падающего фотона ( γ ), рассеянного фотона ( γ ‘) и электрона отдачи ( e ). Угол рассеяния 90°, направление движения электрона отдачи составляет с направлением падающего фотона угол φ =30 o. Если импульс электрона отдачи 3(Мэ. В · с)/м , то импульс рассеянного фотона (в тех же единицах) равен. . . ЗСИ — eppp фф фp φ — ep фp ? ф p φ = 30 º 2/ — epp ф =1, 5 (Мэ. В · с )/м

фp φ — ep фp cos — epp ф 2 3 — ep