Prezentacii com Елементи статистики Підготував студент групи Б-2

Prezentacii. com Елементи статистики Підготував студент групи Б-2 -1 Журенко Максим

Prezentacii. com 1. Статистика - це науковий напрям (комплекс наук), що об'єднує принципи та методи роботи з числовими даними, що характеризують масові явища. 2. Статистика - це галузь практичної діяльності, спрямованої на збір, обробку, аналіз статистичних даних. 3. Статистика - це сукупність статистичних даних, що характеризують яке-нибудь явище чи процес (наприклад, статистика народжуваності і смертності в. Україні, статистика успішності учнів і т. п. ).

Prezentacii. com Ø Одне з найважливіших понять в теорії ймовірностей - випадкова величина. Ø Випадковою величиною називається змінна величина, значення якої залежать від випадкового результату деякого випробування.

Prezentacii. com Ø Статистична інформація про результати спостережень або експериментів може бути представлена в різних формах. Ø Найпростішою з них є запис у порядку їх появи - запис в ряд: Ø Званий простим статистичним рядом або вибіркою.

Prezentacii. com Ø Окремі значення Хi, що становлять цей ряд, називають варіантами або просто даними. Ø Кількість варіант в ряду n називають об'ємом ряду, або обсягом вибірки. Ø Варіанти в ряду можуть мати як різні, так і однакові значення.

Prezentacii. com 3, 4, 5, 6, 6, 6, 5, 1, 4, 6, 1, 4 (n = 12) Ø Варіантами в ряду є Ø Варіанти мають однакові значення.

Prezentacii. com Ø Уявімо ряд даних 3, 4, 5, 6, 6, 6, 5, 1, 4, 6, 1, 4 у вигляді таблиці Х 1 3 4 5 6 М 2 1 3 2 4 Ø У першому рядку - значення випадкової величини Х, у другій - частота значень варіанти М.

Prezentacii. com Ø Відносною частотою події А в даній серії випробувань називають відношення частоти М події А до числа всіх проведених випробувань N. W(A) =

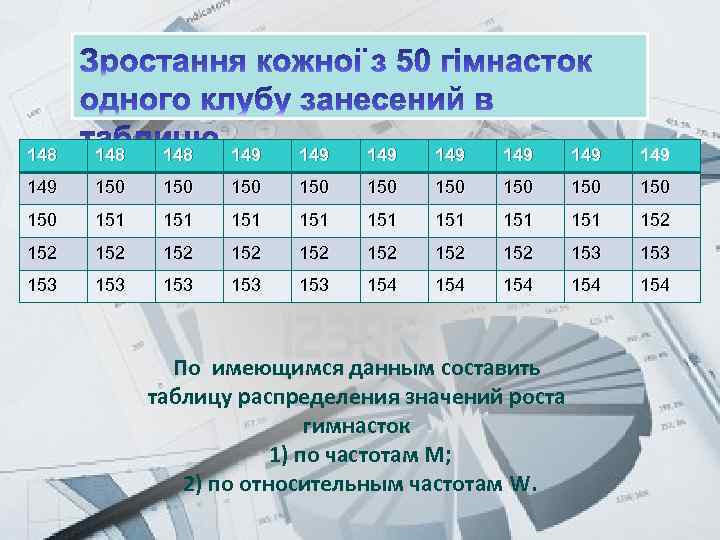
Prezentacii. com 148 148 149 149 150 150 150 151 151 152 152 152 153 153 154 154 154 По имеющимся данным составить таблицу распределения значений роста гимнасток 1) по частотам М; 2) по относительным частотам W.

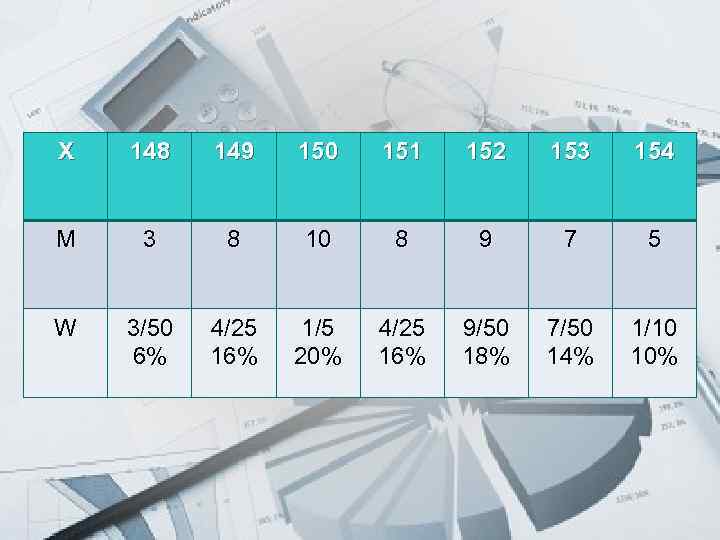
Prezentacii. com X 148 149 150 151 152 153 154 M 3 8 10 8 9 7 5 W 3/50 6% 4/25 16% 1/5 20% 4/25 16% 9/50 18% 7/50 14% 1/10 10%

Prezentacii. com Ø Розподіл випадкових величин можна задавати і демонструвати графічно. Ø Розглянемо приклад. У першому півріччі 2011 року завод отримав прибуток в 10 млн. Рублів. Розподіл прибутку по місяцях показано в таблиці.

Prezentacii. com У координатної площини на осі абсцис будемо відзначати номер місяця (січня. - 1, берез. - 2 і т. д. ). На осі ординат будемо відзначати прибуток заводу (в млн. Руб. ). Відзначимо точки (1; 1, 4), (2; 1, 3), (3; 1, 5), (4; 2, 1), (5, 2), (6; 1, 7) і з'єднаємо їх послідовно відрізками.

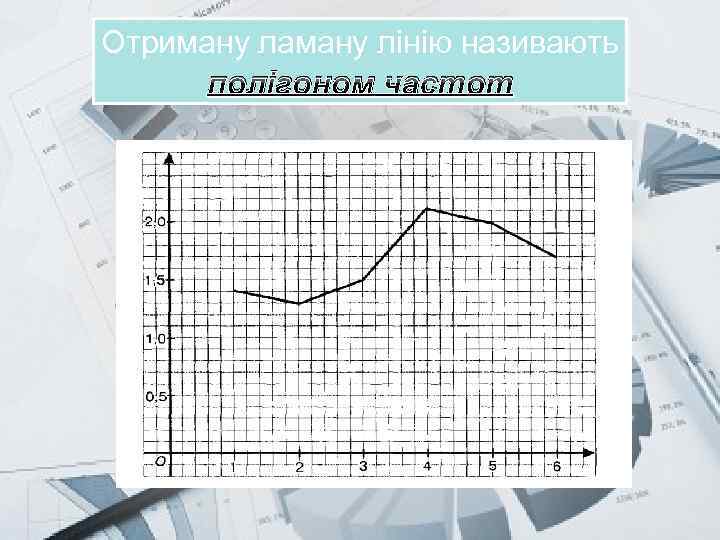
Prezentacii. com Отриману ламану лінію називають полігоном частот

Prezentacii. com Розмах, мода, Медіана. Ø Розмах (R) - різниця між найбільшим і найменшим значеннями варіанти. Ø Мода (Мо) - найбільш часто зустрічається значення варіанти в ряду. Ø Медіана (Ме) - це серединне значення упорядкованого ряду значень випадкової величини.

Prezentacii. com Дано таблиці: 1) розподілу випадкової величини Х - числа прочитаних за канікули книг 10 дівчатками по частотах М. 2) розподілу по частотах випадкової величини У - числа прочитаних книг 9 хлопчиками.

Prezentacii. com Х 3 4 5 8 12 М 3 2 3 1 1 У 3 4 5 6 7 М 2 4 1 1 1

Prezentacii. com Задані таблицями розподілу величин Х і У можуть бути записані у вигляді наступних рядів: 3, 3, 3, 4, 4, 5, 5, 5, 8, 12; (1) 3, 3, 4, 4, 5, 6, 7. (2) Для сукупності (1) R = 12 - 3 = 9. Для сукупності (2) R = 7 -3 = 4. У ряді (1) дві моди: Мо 1 = 3, МО 2 = 5. У ряді (2): Мо = 4.

Prezentacii. com Розглянемо ряд (1) 3, 3, 3, 4, 4, 5, 5, 5, 8, 12. У ряді (1) 10 членів - парне число. Для нього медіана дорівнює середньому арифметичному двох центральних значень п'ятого і шостого: Ме = (4 + 5): 2 = 4, 5.

Prezentacii. com Розглянемо ряд (2) 3, 3, 4, 4, 5, 6, 7. У ряді (2) - непарне число елементів. Його медіана дорівнює значенню центрального п'ятого члена ряду: Ме = 4.

Prezentacii. com Знайти розмах, моду і медіану Сукупності: -2, 3, 4, -3, 0, 1, 3, -2, -1, 2, -2, 1. рішення: Запишемо дані у вигляді упорядкованого ряду: -3, -2, -2, -1, 0, 1, 1, 2, 3, 3, 4. R = 4 - (-3) = 7. Мо = - 2. Ме = (0 + 1): 2 = 0, 5.

Prezentacii. com Средним значением случайной величины Х ( Х ) называют среднее арифметическое всех ее значений.

Prezentacii. com • На соревнованиях по фигурному катанию судьи поставили спортсмену следующие оценки: 5, 2 5, 4 5, 5 5, 4 5, 1 5, 4 5, 5 5, 3 • Для полученного ряда чисел найдите среднее арифметическое, размах, медиану и моду. • Что характеризует каждый из этих показателей?

Prezentacii. com Ø Середнє арифметичне Х ~ 5, 32 характеризує середній рівень оцінок. Ø Розмах А = хmax-хmin = 5, 5 -5, 1 = 0, 4 характеризує розкид оцінок. Ø Мода Мо = 5, 4 показує оцінку, яка зустрічається частіше за інших. Ø Медіана Ме = 5, 4 показує, що половина членів ряду не перевершує за величиною 5, 4.

Prezentacii. com Є середнє значення квадратів відхилень всіх варіант від середнього значення ряду.

Prezentacii. com 1) n=5; 2) n=5; Дисперсия второй выборки больше.

Prezentacii. com Ø Двох футболістів, один з яких брав участь у п'яти ігрових сезонах, а інший - в шести, порівняти по результативності та стабільності в забиванні голів, якщо кількість м'ячів, забитих першим футболістом по сезонах утворює ряд: 17, 21, 20, 16, 15, 19 , а другий: 17, 20, 18, 21, 14.

Prezentacii. com Знаходимо числові характеристики двох вибірок: Перший футболіст: Другий футболіст: Таким чином, обидва футболісти показують однакову результативність (середнє число голів за сезон), але перший футболіст більш стабільний, так як дисперсія першої вибірки менше.

Prezentacii. com 1. Укажите найбільше і найменше значення і розмах набору чисел: 0; -2; 19. 2. Дані два набори чисел: 5; 12; 25 і 3; 6; 12; 26. У якому з наборів розмах більше? 3. Дані набір чисел: 3, 5, 7. Яке число треба до нього додати, щоб розмах нового набору став дорівнює 95. 4. К набору 3; 4; 5 додайте ще одне число, щоб його найбільше значення не змінилося. а) виконайте вимога завдання так, щоб розмах залишився колишнім. б) виконайте вимога завдання так, щоб розмах став більше.

Prezentacii. com 1. На координатної прямої відзначте точки 2; 3; 7 і їх середнє арифметичне. 2. Добавьте до набору чисел 2; 3; 7 таке число, щоб середнє арифметичне залишилося колишнім. 3. . Добавьте до набору чисел 2; 3; 7 таке число, щоб середнє арифметичне стало рівним 5. 4. Среднее арифметичне чисел 85; 25; 68; 78 дорівнює 64. Знайдіть: а) середнє арифметичне - 85; - 25; - 68; - 78; б) середнє арифметичне 170; 50; 136; 156; в) середнє арифметичне 80; 20; 63; 73. 5. У першості школи з футболу команда 7 А класу провела 17 матчів і забила 32 голи, пропустивши при цьому 15 м'ячів. Скільки м'ячів у середньому потрапляло у ворота супротивників цієї команди за кожну гру в шкільному першості?

Prezentacii. com 1. Знайдіть медіани наборів чисел: 686; 478; 834; 706; 843; 698; 549; 112. 2. Дан набір, в якому число 3 зустрічається 1 раз, число 4 - десять разів, а число 5 - сто разів. Інших чисел в наборі немає. Вкажіть медіану даного набору. 3. Вимірюючи вага семи прийшли на урок учнів, вчитель фізкультури отримав ряд чисел: 51, 53, 59, 52, 55, 54, 51. Знайдіть різницю між модою і медіаною даного ряду. 4. У трьох баскетбольних командах виміряли зріст гравців. У першій команді середній зріст склав 195 см, у другій команді медіана ростові дорівнює 197 см, а в третій команді найнижчий спортсмен має зріст 192 см. У кожній команді 7 гравців. З цих команд вирішено набрати нову команду, зріст гравців в якій не менше 193 см. Скільки людина напевно потраплять в цю команду?