Presented at the NY Association of Energy Economics

Presented at the NY Association of Energy Economics 4/26/12 An NSF I/UCRC Could there be a new era with much lower utility bills? Tim Mount Dyson School of Applied Economics and Management Cornell University

Research on the Smart Grid requires collaboration across disciplines Power System Engineering Research Center (PSERC) Researchers at Cornell Engineers Economists Lindsay Anderson Hsiao-Dong Chiang Andrew Hunter Bob Thomas Lang Tong Max Zhang Ray Zimmerman + Alejandro Dominguez-Garcia University of Illinois Carlos Murillo-Sanchez, Universidad Nacional de Colombia 2 Wooyoung Jeon** Alberto Lamadrid** Jung Youn Mo* Surin Maneevitjit** Tim Mount Dick Schuler Bill Schulze Hao Lu* + Dan Shawhan, RPI * Graduate Student, ** Supported by PSERC An NSF I/UCRC

What research do we do at Cornell? Reduced Network for New York State and New England 3 An NSF I/UCRC

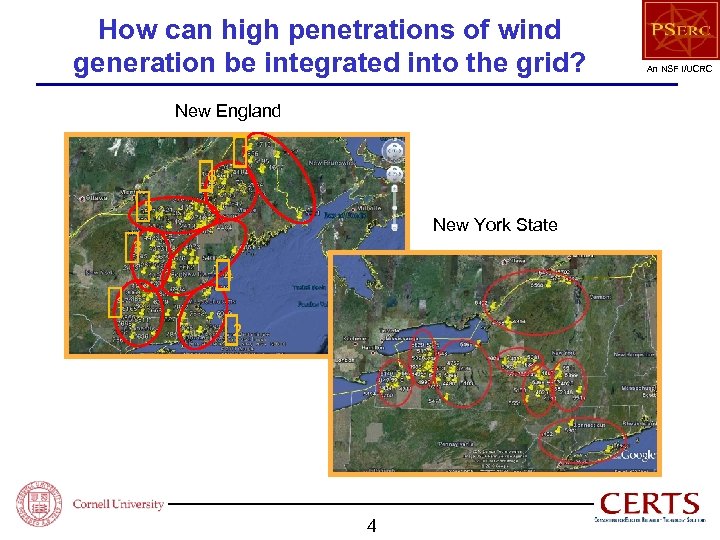How can high penetrations of wind generation be integrated into the grid? New England 7 6 5 New York State 3 4 1 2 4 An NSF I/UCRC

The Problems • The Transition to a Low-Carbon Economy – Electrify the delivery of most energy services (e. g. transportation and heating) – Rely more on variable generation from renewable sources (e. g. wind and solar) – Maintain current standards of reliability • The Economic Effects on Electricity Markets – Lower wholesale prices for electric energy (and lower emissions) because renewable sources displace fossil fuels – Higher amounts of “missing money” for conventional generation and transmission capacity (e. g. Capacity Markets) • The Economic Requirements for a Smart Grid – Customers must see some direct economic benefit – Essential to find substantial cost reductions in operating the conventional generation and transmission system 5 An NSF I/UCRC

Demand for Electricity in New York City for a hot summer day (7/16/10) An NSF I/UCRC • Cumulative Demand for electric energy over 24 hrs: 208 Gwh • Cumulative Temperature-Sensitive Demand over 24 hrs: 74 Gwh • TSD is 35% of the cumulative demand (and 35% of the peak system demand) • Consistent with EIA data (30% of the total electricity demand is used for cooling during the summer) Using an econometric model to distinguish Temperature-Sensitive Demand (TSD) from Non-Temperature-Sensitive Demand (NTSD) TSD is a potentially large source of controllable/deferrable demand 6

Frequent Low Prices Caused by Wind? Five Minute Prices in New York City (2011) An NSF I/UCRC New York City Spot Prices in 2011 10% of prices are above $75/MWh Median spot price is $42/MWh 10% of prices are below $28/MWh 7

An NSF I/UCRC Model I: To illustrate the potential system benefits of controllable/deferrable demand (with no networks constraints) 8

Specifications for the Analysis • 10 GWh of customer storage is added to the system • 5 GWh from electric vehicles (PHEV Volt: 44% penetration) • 5 GWh from thermal storage (Ice batteries: 6% penetration) • A System Operator controls all storage to minimize the total system costs of energy and ramping • The ramping costs are caused by moving the dispatch points of conventional generators (in response to the daily demand profile and the inherent variability of wind generation) • The System Operator determines the market prices for both Energy and Ramping • All customers are assumed to have identical patterns of demand for electrical energy services 9

An NSF I/UCRC System Level Results 10

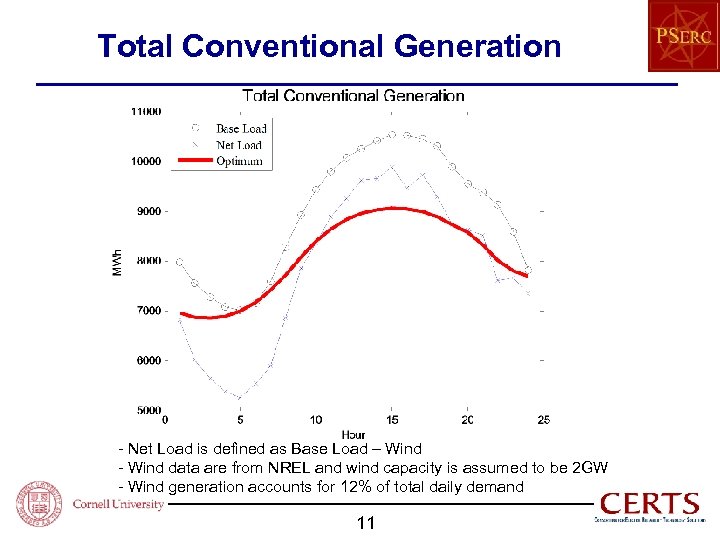Total Conventional Generation - Net Load is defined as Base Load – Wind - Wind data are from NREL and wind capacity is assumed to be 2 GW - Wind generation accounts for 12% of total daily demand 11

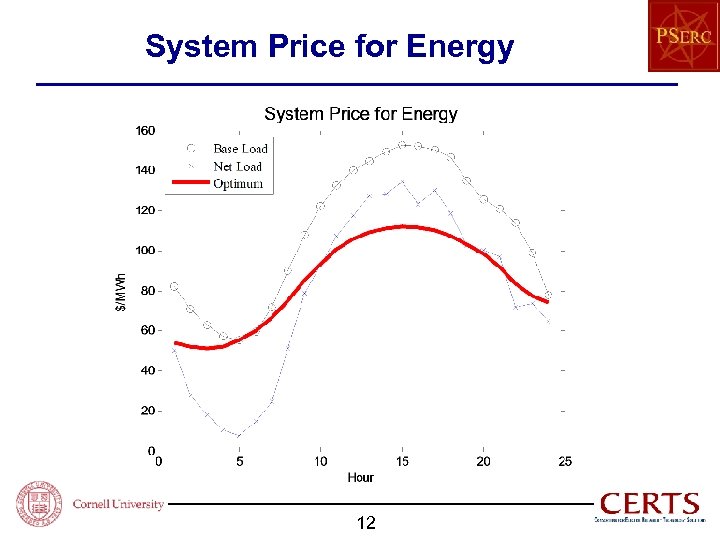System Price for Energy 12

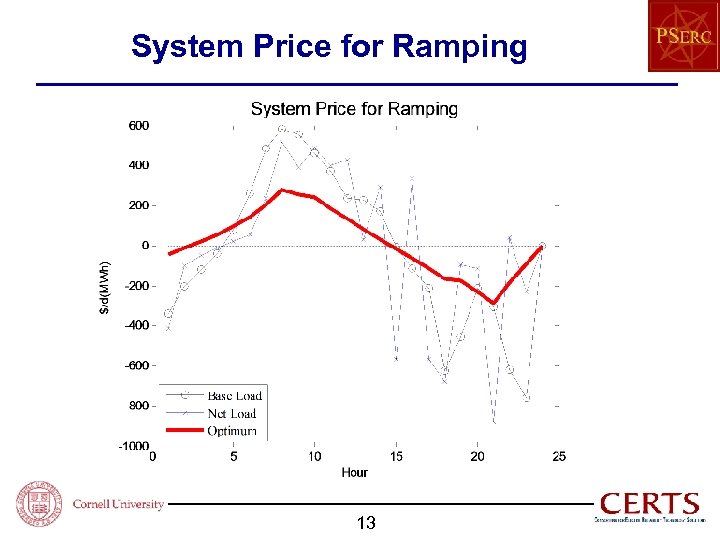System Price for Ramping 13

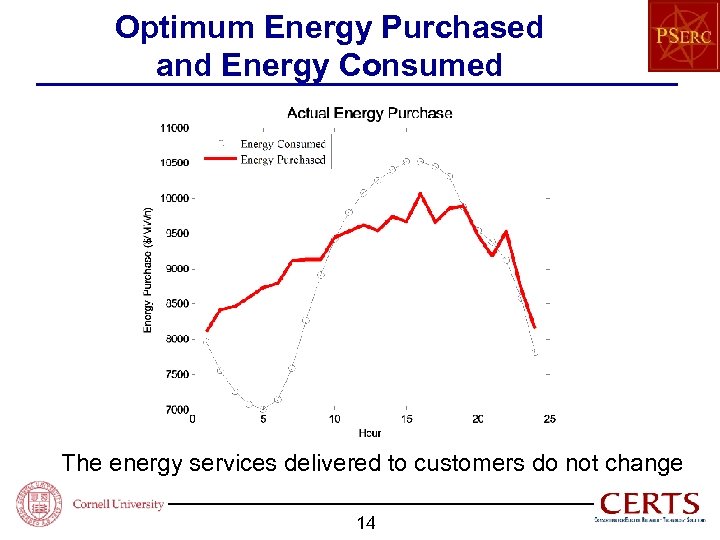Optimum Energy Purchased and Energy Consumed The energy services delivered to customers do not change 14

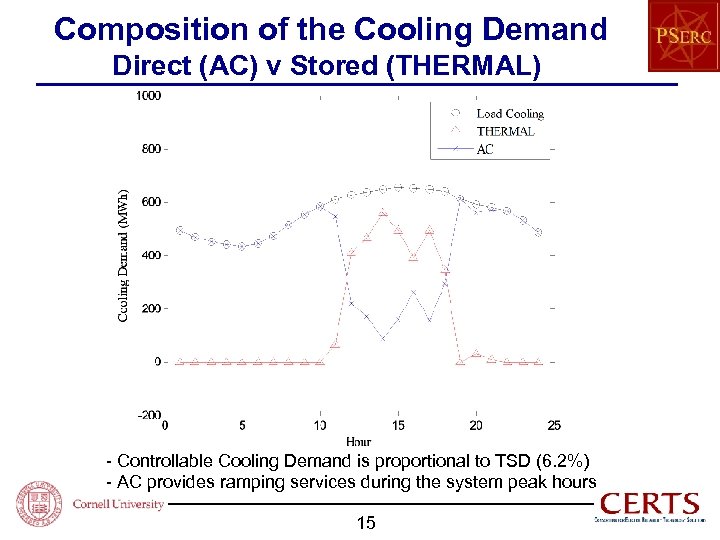Composition of the Cooling Demand Direct (AC) v Stored (THERMAL) - Controllable Cooling Demand is proportional to TSD (6. 2%) - AC provides ramping services during the system peak hours 15

Total System Costs and Total Payments by All Customers Base Load (no Wind) Energy Cost ($1000) Ramping Cost($1000) Total Operating Cost($1000) FEIS(MWh)* Value of FEIS($1000)* Total Cost of Serving Load($1000) Max System Load(MW) Capacity Cost($1000)** TOTAL SYSTEM COST($1000) Total Saving in Gasoline($1000)*** TOTAL COST TO CUSTOMERS % Cost Reduction from Base Load 24, 477 3, 204 27, 681 0 0 27, 681 10, 529 18, 530 46, 211 - Net Load (with Wind) Optimum Load 16, 236 16, 915 3, 855 688 20, 091 17, 603 0 807 0 97 20, 091 17, 506 9, 879 9, 059 17, 386 15, 944 37, 477 33, 451 0 -2, 720 37, 477 30, 731 18. 9% 33. 5% * Final Energy In Storage (FEIS), Valued at $120/MWh (Average Peak Price). ** Annual Capital Cost for Peaker $88 k/MW/year allocated to 100 peak hours. Specify 2 peak hours for this hot day. *** Each vehicle drives 27. 2 Miles at 20 Miles/Gal at $4/Gal. 16 Payment by Customer 19, 069 420 19, 489 - 97 19, 392 - 17, 088 36, 481 -2, 720 33, 761 26. 9%

Composition of the Payments Made to the Regional Transmission Operator Ramping Payment ($1000) Energy Payment ($1000) Total Energy (MWh) Average Payment ($/MWh) 1) CD 2120 18920 21, 041 214911 2) WG 1735 -2154 -419 27070 3) CG -1125 -17236 -18, 361 196822 4) DD -2730 470 -2, 261 12296 Buyers (1)+(2) = 3, 855 (1)+(4) = 19, 390 Suppliers (3)+(4) = -3, 855 (2)+(3) = -19, 390 - Positive (Negative) payments indicate Paying (Being Paid) for a service. - CD, Conventional Demand DD, Deferrable Demand - WG, Wind Generation and CG, Conventional Generation - The SYSTEM COST of ramping is caused by ramping CG - WG accounts for 11% of Energy Supply and 45% of Ramping Demand - CD accounts for 2% of Energy Demand 71% of Ramping Supply 17 98 -15 -93 -184

An NSF I/UCRC Results for Different Types of Customer 18

Consider Four Types of Customer • Assume that there are one million customers with identical initial daily patterns of demand – – Type 1 No storage capabilities Type 2 Add THERMAL storage Type 3 Buy a PHEV Volt Type 4 Both THERMAL and PHEV • All customers pay for: – ENERGY using real-time prices (PHEV can be paid) – CAPACITY at the peak system load – RAMPING using real-time prices (can be paid for reducing the system ramp) 19

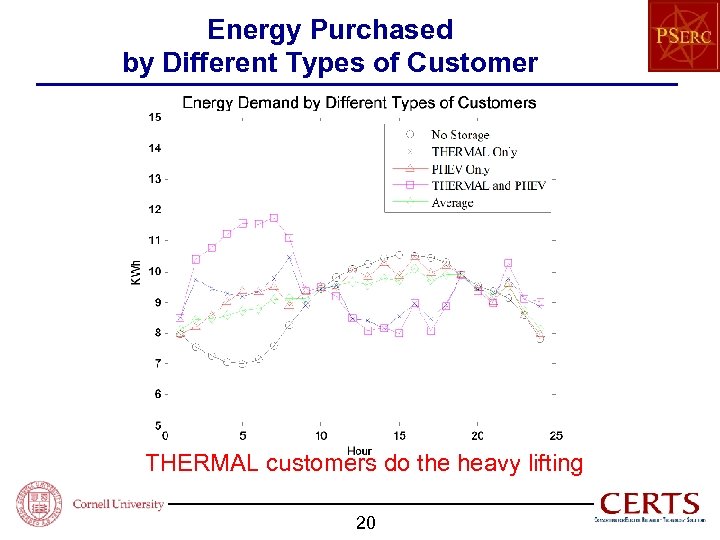Energy Purchased by Different Types of Customer THERMAL customers do the heavy lifting 20

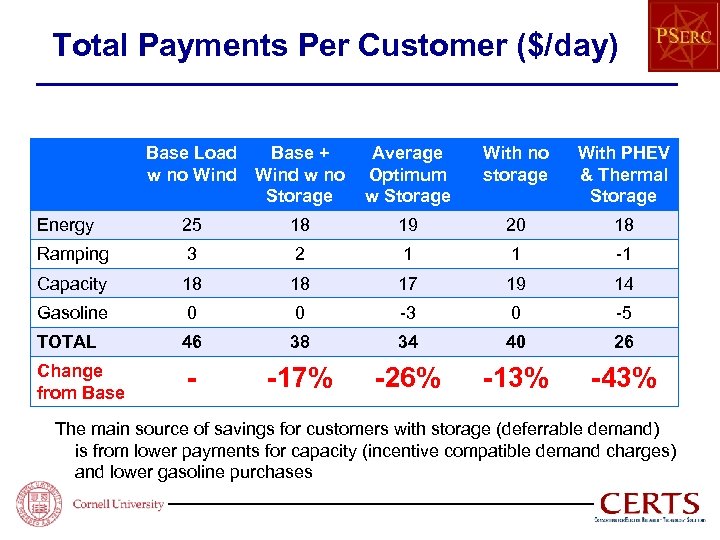Total Payments Per Customer ($/day) Base Load Base + w no Wind w no Storage Average Optimum w Storage With no storage With PHEV & Thermal Storage Energy 25 18 19 20 18 Ramping 3 2 1 1 -1 Capacity 18 18 17 19 14 Gasoline 0 0 -3 0 -5 TOTAL 46 38 34 40 26 Change from Base - -17% -26% -13% -43% The main source of savings for customers with storage (deferrable demand) is from lower payments for capacity (incentive compatible demand charges) and lower gasoline purchases

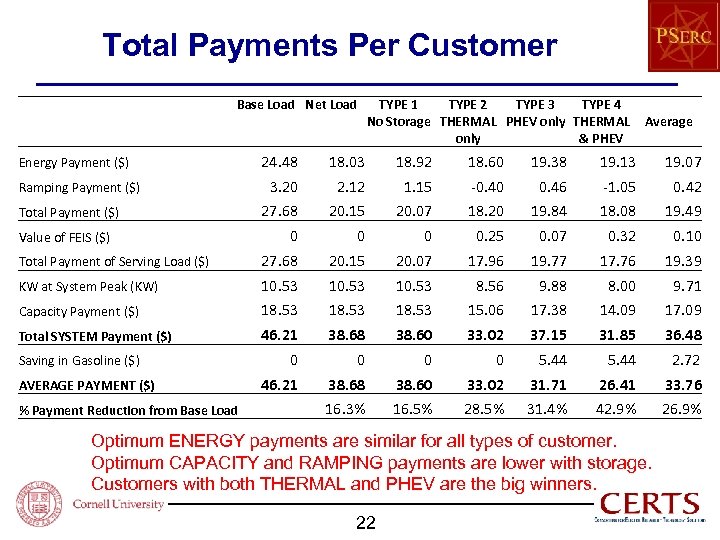Total Payments Per Customer Base Load Net Load TYPE 1 TYPE 2 TYPE 3 TYPE 4 No Storage THERMAL PHEV only THERMAL only & PHEV Average 24. 48 18. 03 18. 92 18. 60 19. 38 19. 13 19. 07 3. 20 2. 12 1. 15 -0. 40 0. 46 -1. 05 0. 42 27. 68 20. 15 20. 07 18. 20 19. 84 18. 08 19. 49 0 0. 25 0. 07 0. 32 0. 10 Total Payment of Serving Load ($) 27. 68 20. 15 20. 07 17. 96 19. 77 17. 76 19. 39 KW at System Peak (KW) 10. 53 8. 56 9. 88 8. 00 9. 71 Capacity Payment ($) 18. 53 15. 06 17. 38 14. 09 17. 09 Total SYSTEM Payment ($) 46. 21 38. 68 38. 60 33. 02 37. 15 31. 85 36. 48 0 0 5. 44 46. 21 38. 68 38. 60 33. 02 31. 71 26. 41 33. 76 16. 3% 16. 5% 28. 5% 31. 4% 42. 9% 26. 9% Energy Payment ($) Ramping Payment ($) Total Payment ($) Value of FEIS ($) Saving in Gasoline ($) AVERAGE PAYMENT ($) % Payment Reduction from Base Load 5. 44 2. 72 Optimum ENERGY payments are similar for all types of customer. Optimum CAPACITY and RAMPING payments are lower with storage. Customers with both THERMAL and PHEV are the big winners. 22

Total Payments Per Customer Using a Flat Regulated Price for Energy Types of Customer No Storage THERMAL only PHEV only 224. 4 THERMAL Average & PHEV Energy Purchased (KWh) 214. 9 220. 1 Savings in Gasoline ($) - - OPTIMUM Price Payment ($)* 38. 60 33. 02 37. 15 Change from Average (%) 5. 8% -9. 5% 1. 8% -12. 7% - FLAT PRICE Payment ($)** 35. 48 36. 33 37. 05 38. 01 36. 48 Change from Average (%) -2. 7% -0. 4% 1. 6% 4. 2% - 5. 44 230. 2 221. 0 5. 44 2. 72 31. 85 36. 48 * Gasoline Cost Savings are excluded. ** Flat Price Payment is scaled so that average payments for Flat Price and Optimum Price are equal THE REGULATORY PROBLEM FOR RETAIL CUSTOMERS Most retail customers pay bills for electricity that are determined by their use of energy. Consequently, the economic incentives for investing in thermal storage are perverse. 23

An NSF I/UCRC Conclusions 24

CONCLUSIONS • High penetrations of renewable generation lower the wholesale price of energy BUT increase the ramping and capacity costs (“missing money”) for the conventional generators • Wholesale customers and aggregators who have deferrable demand should get substantial economic benefits by: – Purchasing more energy at less expensive off-peak prices – Reducing their demand (capacity) during expensive peak-load periods – Selling ancillary services (ramping) to mitigate wind variability • All market participants should pay for the services they use and get paid for the services they provide • Most existing retail rate structures do not provide the correct economic incentives for deferrable demand 25

Issues for Future Research (Issues for regulators are RED) • The economic benefits of deferrable demand for the grid are not adequately represented by the current rates charged to customers – Customers (aggregators) should pay real-time prices for energy – Correct measurement and payments needed for each customer’s peak demand – Customers should pay/get paid for using/supplying ramping services • The inherent variability of generation from renewable sources and the difficulty of forecasting these sources accurately are incompatible with the current structure of day-ahead markets and unit commitment – Need a rolling horizon for optimizing real-time dispatch that uses updated forecasts of potential renewable generation and system conditions (e. g. like Australia) – Customers (aggregators) should get updated (non-binding) projections of future prices at least 24 hours ahead to manage storage efficiently (e. g. like Australia) • The structures/capabilities of existing distribution networks are major weak links in the electric delivery system for a future smart grid – Need new scheduling algorithms for coordinating multiple stochastic sinks of deferrable demand to improve grid efficiency and for accommodating multiple sources of variable generation from renewable sources of energy 26