Вводная лекция_2.ppt
- Количество слайдов: 26
Преподаватель курса Юрасов Александр Борисович Теория оптимального управления экономическими системами

Оптимальность - (от лат. optimus - наилучший) наилучший способ экономического поведения, экономических действий (экономический словарь)

Цели оптимизации деятельности экономических систем Разработка управляющего воздействия, обеспечивающего достижение запланированного результата Минимизация затрат, издержек при имеющихся ограничениях Максимизация выгоды от деятельности при имеющихся ограничениях Получение запланированного экономического результата в течении заранее установленного времени Определение промежуточных состояний экономической системы, при которых достижение запланированных магистральных значений происходит плавно, в пределах допустимых рисков и др.

Объекты оптимизации В частности, оптимизируются такие операции, как: • портфель заказов производственных систем; • распределение ресурсов между экономическими системами; • распределение годовой производственной программы предприятия по кварталам; • стратегия использования оборудования на предприятии; • управление производственными запасами; • сетевое планирование; • прогнозирование экономических процессов и др.

Теория оптимального управления Предметом изучения ТОУЭС являются системы управления хозяйствующими объектами.
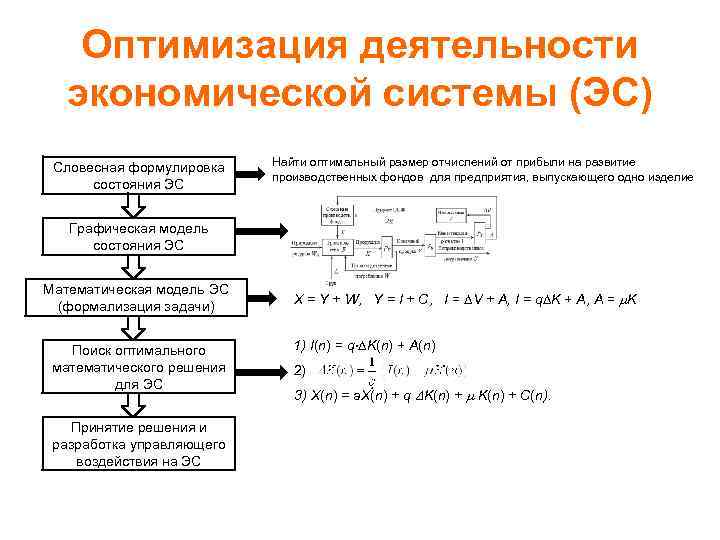
Оптимизация деятельности экономической системы (ЭС) Словесная формулировка состояния ЭС Найти оптимальный размер отчислений от прибыли на развитие производственных фондов для предприятия, выпускающего одно изделие Графическая модель состояния ЭС Математическая модель ЭС (формализация задачи) Поиск оптимального математического решения для ЭС Принятие решения и разработка управляющего воздействия на ЭС X = Y + W, Y = I + C, I = V + A, I = q K + A, A = K 1) I(n) = q K(n) + A(n) 2) 3) X(n) = a. X(n) + q K(n) + C(n).
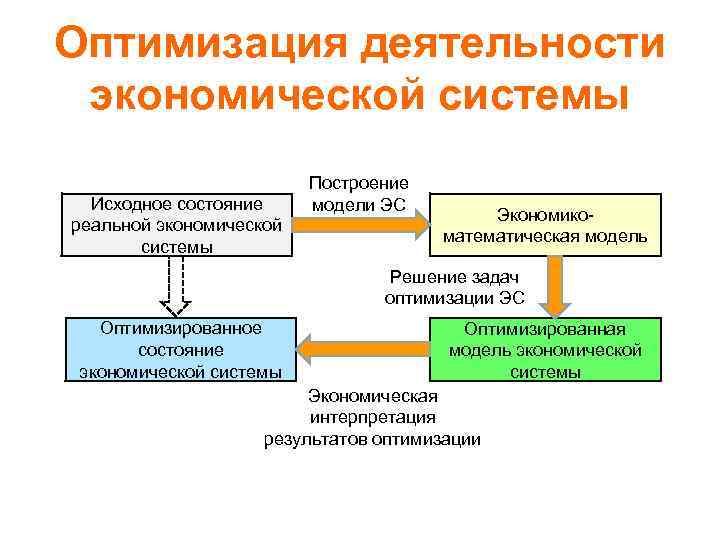
Оптимизация деятельности экономической системы Исходное состояние реальной экономической системы Построение модели ЭС Экономикоматематическая модель Решение задач оптимизации ЭС Оптимизированное состояние экономической системы Оптимизированная модель экономической системы Экономическая интерпретация результатов оптимизации
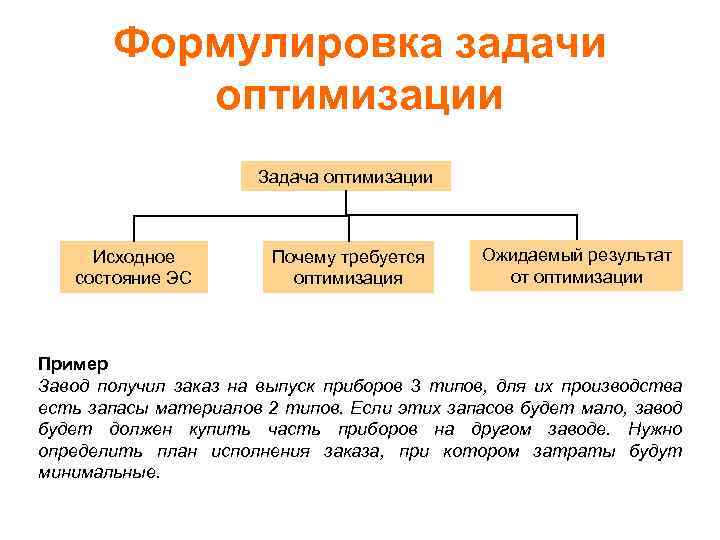
Формулировка задачи оптимизации Задача оптимизации Исходное состояние ЭС Почему требуется оптимизация Ожидаемый результат от оптимизации Пример Завод получил заказ на выпуск приборов 3 типов, для их производства есть запасы материалов 2 типов. Если этих запасов будет мало, завод будет должен купить часть приборов на другом заводе. Нужно определить план исполнения заказа, при котором затраты будут минимальные.
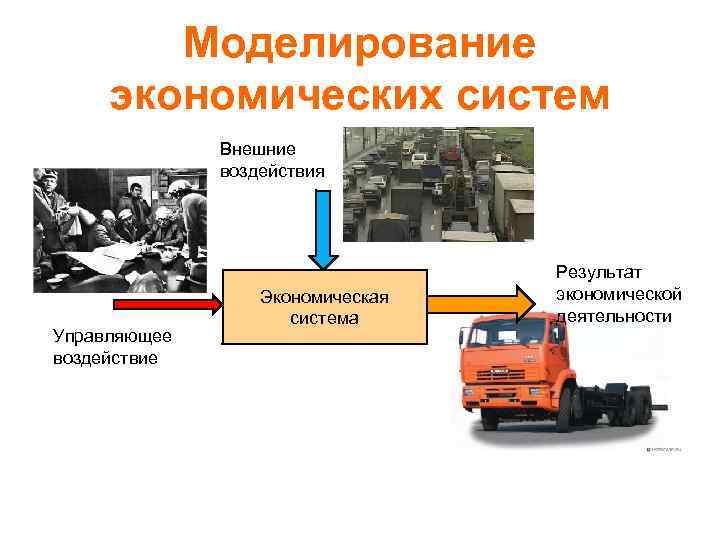
Моделирование экономических систем Внешние воздействия Управляющее воздействие Экономическая система Результат экономической деятельности
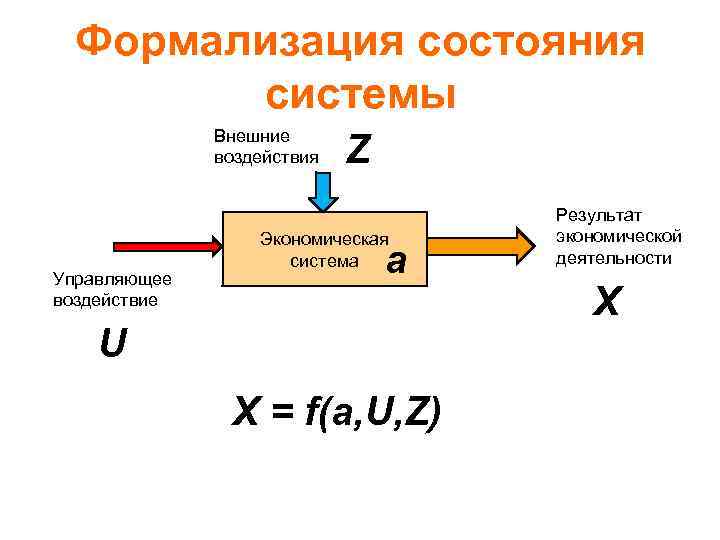
Формализация состояния системы Внешние воздействия Управляющее воздействие Z Экономическая система a U Х = f(a, U, Z) Результат экономической деятельности Х
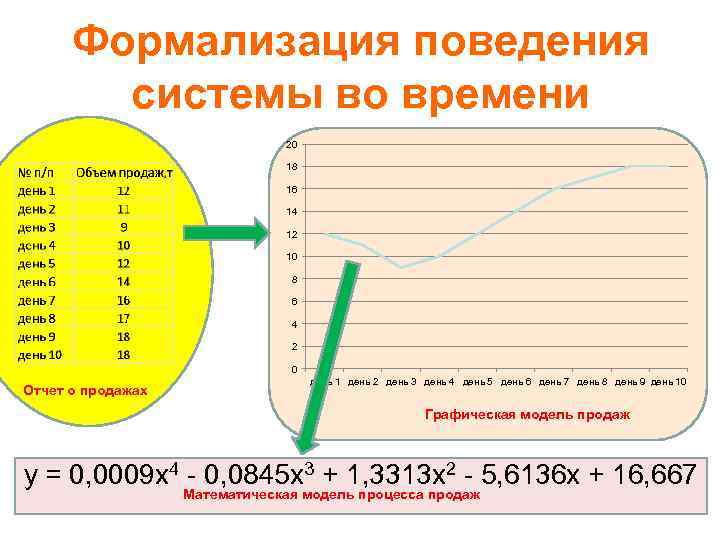
Формализация поведения системы во времени 20 18 16 14 12 10 8 6 4 2 0 Отчет о продажах день 1 день 2 день 3 день 4 день 5 день 6 день 7 день 8 день 9 день 10 Графическая модель продаж y = 0, 0009 x 4 - 0, 0845 x 3 + 1, 3313 x 2 - 5, 6136 x + 16, 667 Математическая модель процесса продаж
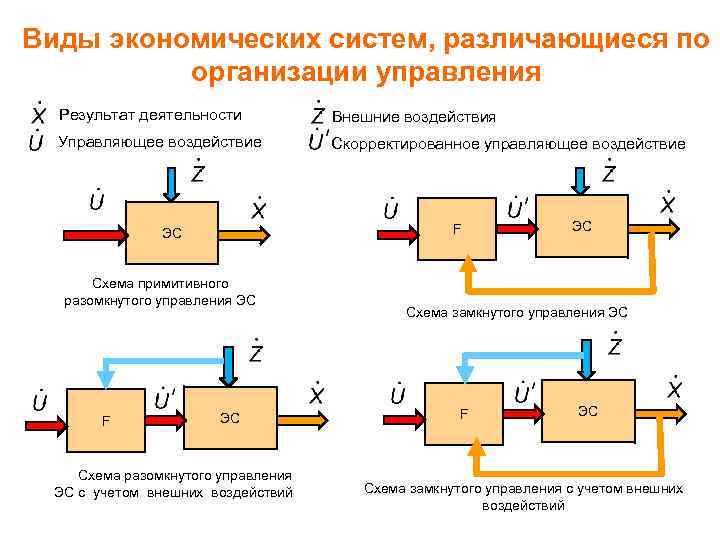
Виды экономических систем, различающиеся по организации управления Результат деятельности Внешние воздействия Управляющее воздействие Скорректированное управляющее воздействие F ЭС Схема примитивного разомкнутого управления ЭС F ЭС Схема разомкнутого управления ЭС с учетом внешних воздействий ЭС Схема замкнутого управления ЭС F ЭС Схема замкнутого управления с учетом внешних воздействий
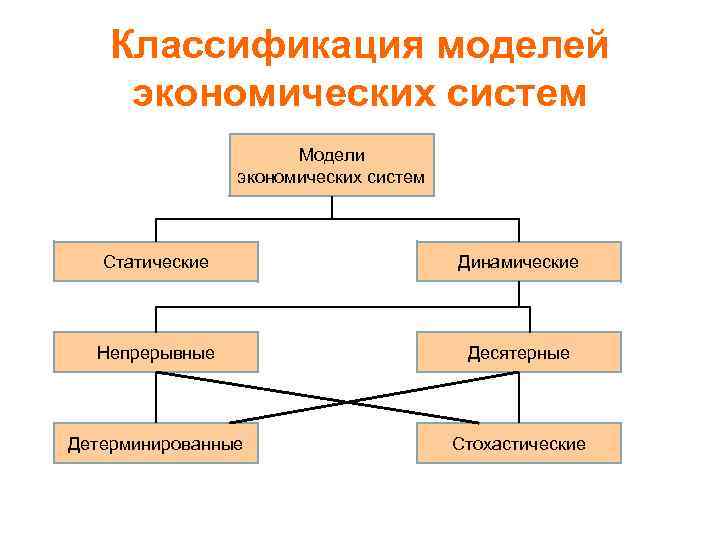
Классификация моделей экономических систем Модели экономических систем Статические Динамические Непрерывные Десятерные Детерминированные Стохастические

Статическая экономическая система Под статической экономической системой понимается такая система, координаты которой на изучаемом отрезке времени могут рассматриваться как постоянные. При этом подразумевается, что: • • все зависимости относятся к одному моменту времени, а моделируемая система неизменна во времени полностью игнорируются возможные (а подчас даже неизбежные) изменения, поскольку их учет не требуется для достижения цели моделирования все интересующие процессы, происходящие в системе, не требуют при своем описании развертывания во времени, так как могут быть с достаточной степенью точности охарактеризованы не зависящими от времени величинами, как известными, так и неизвестными фиксированный момент времени может представлять целый временной интервал, как правило, в качестве его конечной, средней или начальной точки, в течение которого система предполагается неизменной. Примеры статических моделей межотраслевого баланса, сводимые к; • транспортной задаче • распределительной задаче линейного программирования (в частности, некоторые статические модели размещения производства) • задачам о потоках в сетях и т. д.
Пример статической модели предприятия

. Динамическая экономическая система Под динамической системой понимается всякая система, изменяющаяся во времени. Математически это принято выражать через переменные, которые часто называются координатами. Процесс изменения переменных характеризуется траекторией: где координаты q 1(t), q 2(t), … qn(t) являются функциями времени t. Математическое описание динамических моделей производится: • системами дифференциальных уравнений (где время выступает в качестве непрерывной переменной); • разностных уравнений (где время дискретная величина); • систем обыкновенных алгебраических уравнений. С помощью динамических моделей, в частности, решаются задачи планирования и прогнозирования экономических процессов: • определения траектории развития экономической системы и ее состояний в заданные моменты времени; • анализа экономической системы на устойчивость; • анализа структурных сдвигов

Основные термины и понятия в ТОУЭС Задача оптимального управления - это получение в определенном смысле наилучшего результата управления. Критерий оптимального управления - это словесная и (или) математическая формулировка наилучшего результата. Последнюю называют также критерием качества или целевой функцией. Целевая функция - это математическая зависимость результата от состояния системы, от внешних возмущений и от управления. Математическая модель системы - это совокупность математических формул, таблиц, графиков, устанавливающих зависимость между состоянием системы, внешними воздействиями, управлением системой и временем. Иными словами математическая модель описывает эволюцию системы в зависимости от перечисленных факторов.

Целевая функция: статические модели Линейная целевая функция от независимых переменных xi, известные коэффициенты сi в этой функции часто называют весовыми коэффициентами или коэффициентами значимости (стоимости) переменных где i - весовые коэффициенты для каждого вида целевой функции, m - число критериев. Нелинейная целевая функция от независимых переменных xi имеет вид: где m – gпорядковый номер переменной
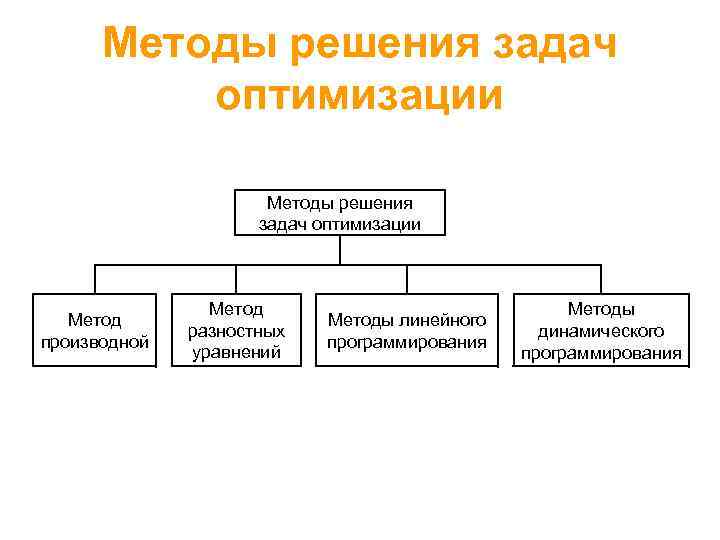
Методы решения задач оптимизации Метод производной Метод разностных уравнений Методы линейного программирования Методы динамического программирования

Метод производных Суть метода в нахождении точки экстремума для непрерывной и дифференцируемой функции y = f(x), которая описывает состояние системы. Т. е. вычисление точки при которой обращается в нуль производная функции f(x) по переменной x.

Метод разностных уравнений Процессы, происходящие в дискретных экономических моделях, описываются разностными уравнениями. Такие уравнения возникают всегда, когда состояние системы в следующем цикле зависит от состояния системы в предыдущем цикле, от управления системой и от внешних факторов. Пример. Бизнесмен открыл счет в банке, положив на счет сумму S 0 под определенный банковский процент r. Необходимо составить уравнение, описывающее изменение суммы на счету бизнесмена от цикла к циклу. Если банковский коэффициент ri не зависит от номера цикла, т. е. ri =r= const, то сумма на счету в конце i-ого цикла составит: Si = Si - 1 (1 + r) = Si - 2 (1 + r)2 = Si - 3 (1 + r)3 = = S 0 (1 + r)i = kcл S 0, где kсл = (1 + r)i - сложный банковский процент. По формуле сумма на счету может быть определена на любом цикле. Эта формула может быть применена только при r = const, т. е. когда банковский процент r не зависит от номера цикла i.

Общая форма записи разностных уравнений Общая форма записи разностного уравнения порядка m имеет следующий вид: Приняв коэффициент а 0 = 1, это уравнение можно записать в виде: В этом уравнении n - номер цикла, i - задержка по циклам, bi - коэффициенты нерекурсивной части уравнения при переменных х(n - i), ai - коэффициенты рекурсивной части уравнения при переменных y(n - i).

Общая формулировка задачи линейного программирования Задана система m линейных алгебраических уравнений с n неизвестными: и линейная функция относительно переменных х1, х2, , хn: Требуется найти такие неотрицательные значения переменных х1, х2, … хn, которые бы удовлетворяли системе линейных уравнений и обращали в максимум линейную функцию F(x)= max

Методы динамического программирования (ДП) Метод динамического программирования (метод Гамильтона-Якоби. Беллмана) ориентирован на поиск оптимального управления широкого класса систем, в том числе для: • решения задач планирования, • распределение ресурсов, • снабжения, • разрешения игровых ситуаций, • построение алгоритмов решения задач и т. д. ДП применяется для оптимизации динамических и статических систем, для детерминированных и стохастических систем Принцип ДП формулируется следующим образом: оптимальное управление не зависит от предыстории процесса изменения состояния системы, а определяется лишь ее состоянием в рассматриваемый момент времени
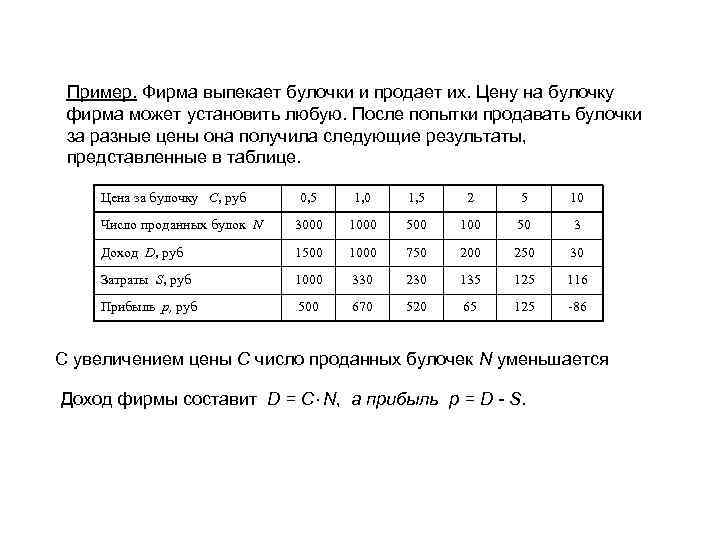
Пример. Фирма выпекает булочки и продает их. Цену на булочку фирма может установить любую. После попытки продавать булочки за разные цены она получила следующие результаты, представленные в таблице. Цена за булочку С, руб 0, 5 1, 0 1, 5 2 5 10 Число проданных булок N 3000 1000 500 100 50 3 Доход D, руб 1500 1000 750 200 250 30 Затраты S, руб 1000 330 230 135 125 116 Прибыль р, руб 500 670 520 65 125 -86 С увеличением цены С число проданных булочек N уменьшается Доход фирмы составит D = C N, а прибыль р = D - S.
Автоматическое управление
Вводная лекция_2.ppt