Преподавание курса Методы внутренних точек Зоркальцев В И

Преподавание курса «Методы внутренних точек» Зоркальцев В. И. , д. т. н. , проф. , ИГУ, кафедра мат. экономики Филатов А. Ю. , к. ф. -м. н. , доцент ИГУ, кафедра мат. экономики Работа выполнена при финансовой поддержке РФФИ (проект 05 -01 -00587 а) Высшая математика Математический анализ Методы оптимизации Линейное программирование Методы внутренних точек

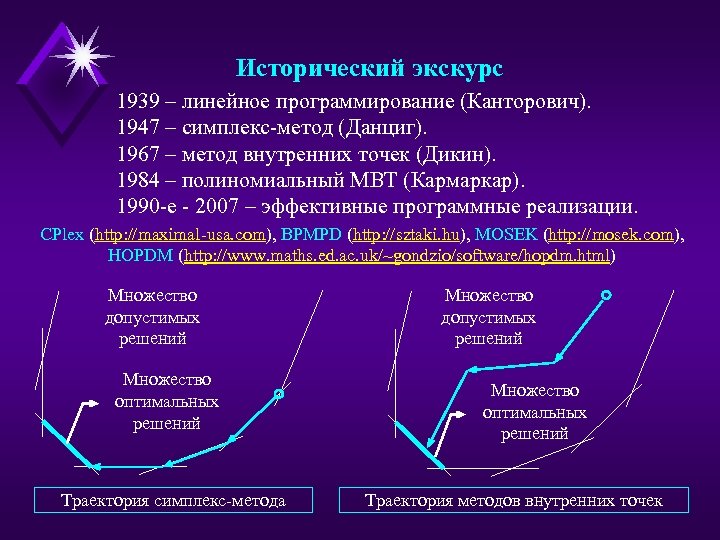Исторический экскурс 1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984 – полиномиальный МВТ (Кармаркар). 1990 -е - 2007 – эффективные программные реализации. CPlex (http: //maximal-usa. com), BPMPD (http: //sztaki. hu), MOSEK (http: //mosek. com), HOPDM (http: //www. maths. ed. ac. uk/~gondzio/software/hopdm. html) Множество допустимых решений Множество оптимальных решений Траектория симплекс-метода Множество допустимых решений Множество оптимальных решений Траектория методов внутренних точек

Аффинно-масштабирующие алгоритмы внутренних точек Пара взаимно-двойственных задач ЛП: (1) (2) Стартовое приближение: Итеративный переход: Направление корректировки: (3) Шаг корректировки:

Алгоритмы центрального пути (обладают полиномиальными оценками) Логарифмическая барьерная функция: (4) Параметризация в комбинированных алгоритмах: (5) Преимущества алгоритмов внутренних точек • Удобная адаптация к задачам в нестандартной постановке. • На каждой итерации идет улучшение всех переменных. • Решение – относительно внутренняя точка множества оптимальных решений. • Наличие у ряда алгоритмов полиномиальных оценок максимального объема вычислений.

Примерная программа курса «Методы внутренних точек» (34 ч. ) 1. Теоретические основы линейной оптимизации • Пара взаимно-двойственных задач линейного программирования. • Основные факты теории двойственности. 2. Аффинно-масштабирующие алгоритмы для решения задач линейного программирования • Истоки алгоритмов внутренних точек. • Прямые аффинно-масштабирующие алгоритмы. • Способы задания весовых коэффициентов. • Ввод в допустимую область. • Двойственные аффинно-масштабирующие алгоритмы.

Примерная программа курса «Методы внутренних точек» (34 ч. ) 3. Полиномиальные алгоритмы для решения задач линейного программирования • Исторический экскурс в полиномиальные алгоритмы. • Идейная основа и общая схема алгоритмов центрального пути. • Простейший вариант алгоритма центрального пути. • Процедуры, ускоряющие вычислительный процесс. • Двойственные алгоритмы центрального пути. • Проблема инициализации алгоритмов. Два способа ее решения путем перехода к расширенным задачам специального вида. • Алгоритмы скошенного пути. • Комбинированные алгоритмы.

Примерная программа курса «Методы внутренних точек» (34 ч. ) 4. Решение систем линейных неравенств • Метод Фурье-Черникова. • Метод сведения к задаче линейного программирования с одной дополнительной переменной. • Случай интервальных ограничений на переменные. • Быстрая идентификация несовместности системы. 5. Обращение симметричной положительно определенной матрицы • Метод Гаусса. • Метод Халецкого. • Метод сопряженных направлений. • Техника частичного обновления.

Примерная программа курса «Методы внутренних точек» (34 ч. ) 6. Примеры практического приложения алгоритмов внутренних точек • Задача поиска допустимых режимов электроэнергетических систем. • Задача идентификации состояния электроэнергетических систем. • Задача оценки дефицита мощности электроэнергетической системы Информация о данном курсе в интернете • http: //polnolunie. baikal. ru/me/mat_prog. htm • http: //math. isu. ru/filatov • E-mail: alexander. filatov@gmail. com

Спасибо за внимание! http: //math. isu. ru/filatov, http: //polnolunie. baikal. ru/me, http: //fial_. livejournal. com, alexander. filatov@gmail. com