Преобразование графиков функций. n

Преобразование графиков функций.

n График функции f(х+t) получается параллельным переносом графика f(х) в отрицательном направлении оси Ох на │t│ при t>0 и в положительном направлении на │t│ при t<0.

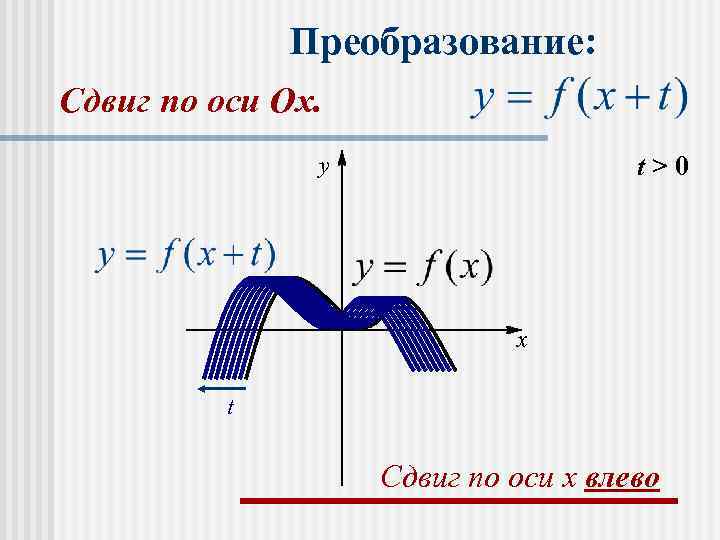
Преобразование: Сдвиг по оси Оx. y t>0 x t Сдвиг по оси x влево

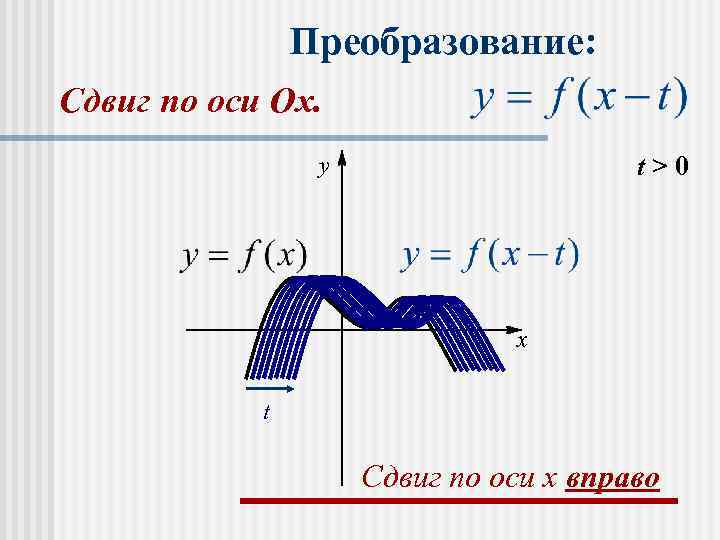
Преобразование: Сдвиг по оси Оx. y t>0 x t Сдвиг по оси x вправо

n График функции f(х)+m получается параллельным переносом графика f(х) в положительном направлении оси Оу на m при m>0 и в отрицательном направлении этой оси на │m│ при m<0.

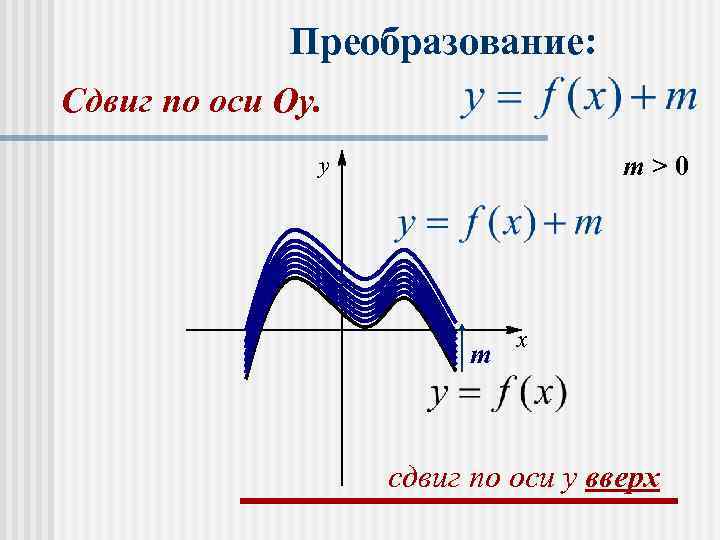
Преобразование: Сдвиг по оси Оу. y m>0 x m сдвиг по оси y вверх

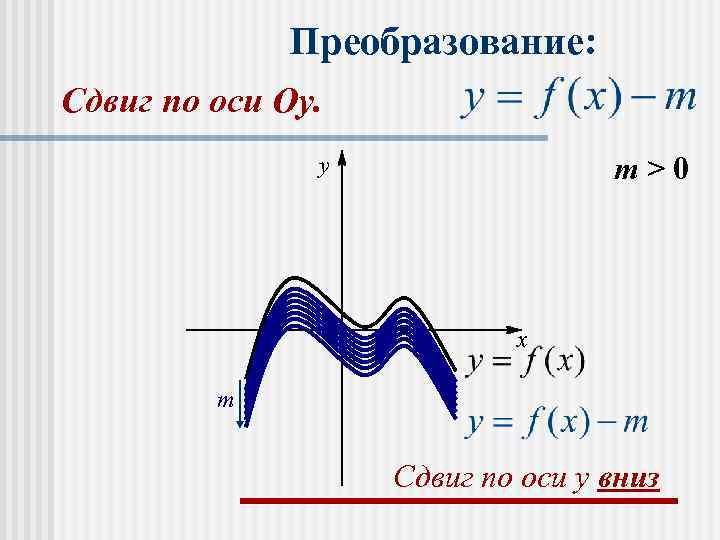
Преобразование: Сдвиг по оси Оу. y m>0 x m Сдвиг по оси y вниз

n График функции f(bх) получается сжатием графика f(х) в b раз к оси Оу при b>1 или растяжением в раз от этой оси Оу при 0

Преобразование: Сжатие по оси x. y k>1 x k Сжатие по оси x

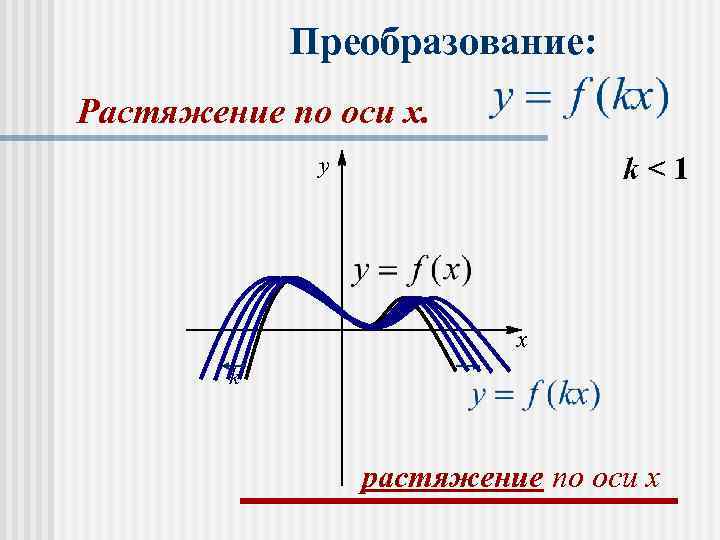
Преобразование: Растяжение по оси x. y k<1 x k растяжение по оси x

n График функции af(х) получается растяжением графика f(х) вдоль оси Оу в а раз при а>1 и сжатием вдоль этой оси в раз при 0<а<1.

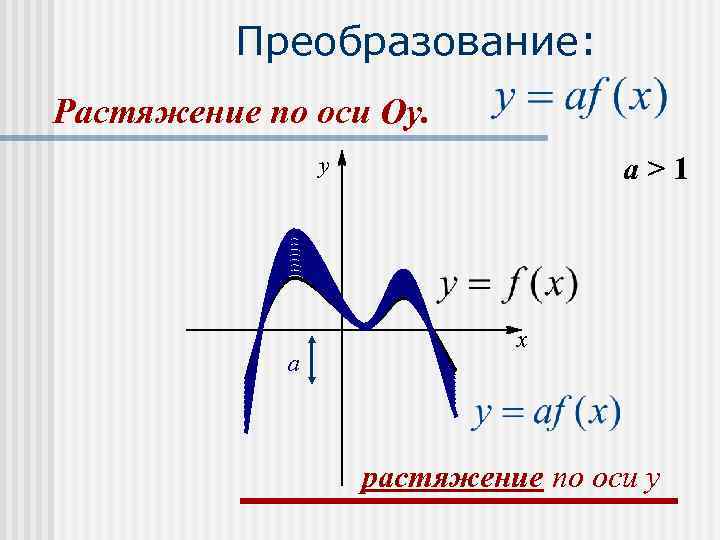
Преобразование: Растяжение по оси Оу. y a>1 x a растяжение по оси y

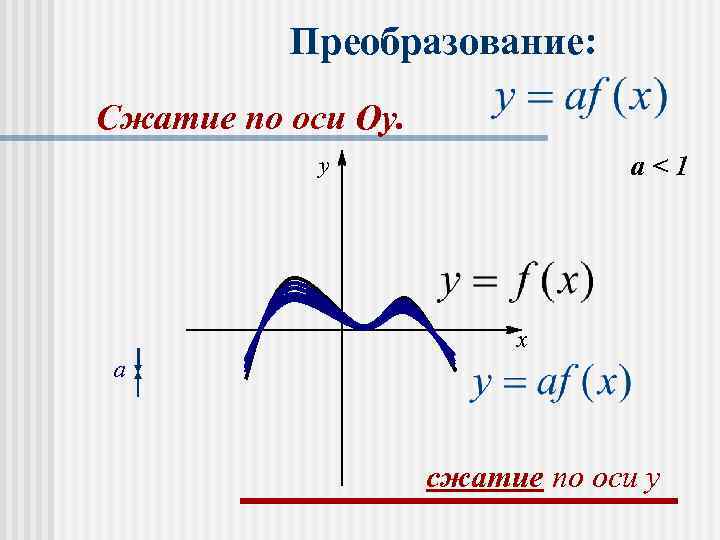
Преобразование: Сжатие по оси Оу. y a<1 x a сжатие по оси y

n График функции у=f(-х) получается симметричным отображением графика f(х) относительно оси Оу. у f(-х) f(х) 0 х

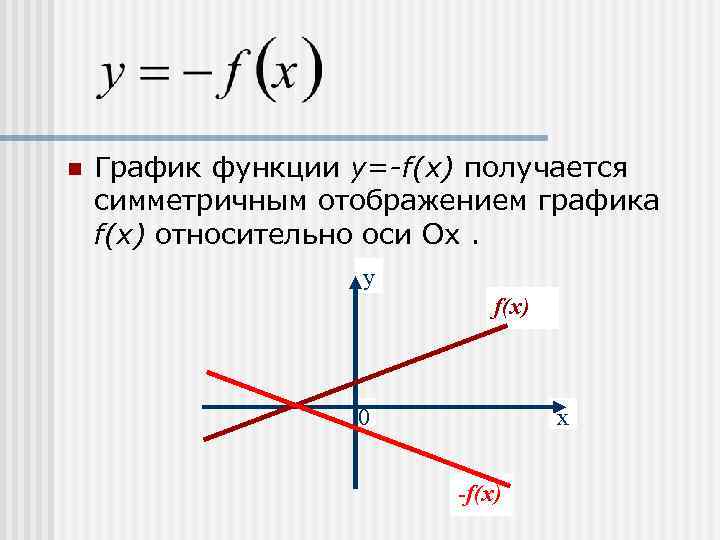
n График функции у=-f(х) получается симметричным отображением графика f(х) относительно оси Ох. у f(x) 0 х -f(x)

n График функции у=│f(х)│ получается из графика функции у=f(х) у │f(x)│ следующим образом: часть графика у=f(х), лежащая над осью Ох, сохраняется, часть его, 0 х лежащая под осью Ох, f(x) отображается симметрично относительно оси Ох.

n График функции у=f(│х│) получается f(│x│) у f(x) из графика функции у=f(х) следующим образом: при х≥ 0 график у=f(х) сохраняется, а при 0 х х<0 полученная часть графика отображается симметрично.

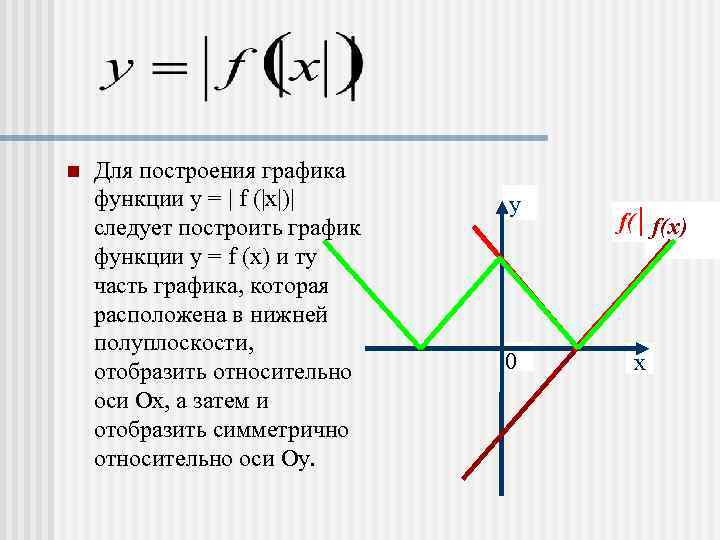
n Для построения графика функции у = | f (|х|)| у следует построить график f(│x│) f(x) функции у = f (х) и ту часть графика, которая расположена в нижней полуплоскости, отобразить относительно 0 х оси Ох, а затем и отобразить симметрично относительно оси Оу.

n График следует строить по точкам, складывая или вычитая ординаты графиков функций f(х) и g(х), соответствующие одному и тому же значению аргумента.