Преобразование Барроуза – Уиллера. Создатели Впервые он был

Преобразование Барроуза – Уиллера

Создатели Впервые он был опубликован 10 мая 1994 г. Авторами метода являются David John Wheeler и Michael Burrows

Создатели Причем Дэвид Уилер придумал этот метод еще в 1983 г., когда работал в компании AT&T Bell Laboratories. Но, видимо, либо тогда не придал значения своему открытию, либо посчитал чрезмерными требования к вычислительным ресурсам.

Предназначение Преобразование Барроуза - Уилера предназначено для того, чтобы преобразовать входной блок в более удобный для сжатия вид. Причем полученный в результате преобразования блок обычные методы сжимают не так эффективно, как методы, специально для этого разработанные.

Предназначение В оригинальной статье была предложена как одна из возможных реализаций сжатия на основе BWT совокупность из трех алгоритмов: преобразования Барроуза - Уилера; преобразования Move – To – Front (перемещение стопки книг); статистического кодера для сжатия данных, полученных в результате последовательного применения двух вышеупомянутых преобразований.

Предназначение Дальнейшие исследования показали, что второе из перечисленных преобразований не является необходимым и может быть заменено альтернативным (например, RLE). Или даже исключено вовсе за счет усложнения кодирующей фазы. Впрочем, сами авторы BWT упоминали о такой возможности.

Предназначение Прежде всего следует отметить одну из его особенностей. Он оперирует сразу целым блоком данных. То есть ему заранее известны сразу все элементы входного потока или по крайней мере достаточно большого блока. Это делает затруднительным использование алгоритма в тех областях применения, где требуется сжатие данных "на лету", символ за символом.

Процесс сжатия Имеем блок данных, далее создаем матрицу всех возможных его циклических перестановок. Первой строкой матрицы будет исходная последовательность, второй строкой - она же, сдвинутая на один символ влево, и т. д. Рассмотрим применения преобразования на фразе «абракадабра»

Процесс сжатия

Процесс сжатия Пометим в этой матрице исходную строку и отсортируем все строки в соответствии с лексикографическим порядком символов. Будем считать, что одна строка должна находиться в матрице выше другой, если в самой левой из позиций, начиная с которой строки отличаются, в этой строке находится символ лексикографически меньший, чем у другой строки.

Процесс сжатия Другими словами, следует отсортировать символы сначала по первому символу, затем строки, у которых первые символы равны, - по второму и т. д.

Процесс сжатия

Процесс сжатия Теперь остался последний шаг - выписать символы последнего столбца и запомнить номер исходной строки среди отсортированных. Итак, рдакраааабб,2 - это результат, полученный в результате преобразования Барроуза - Уилера.

Процесс восстановления Пусть нам известны только результат преобразования, т. е. последний столбец матрицы, и номер исходной строки. Рассмотрим процесс восстановления исходной матрицы. Для этого отсортируем все символы последнего столбца

Процесс восстановления Нам известно, что строки матрицы были отсортированы по порядку, начиная с первого символа. Поэтому, очевидно, в результате такой сортировки мы получили первый столбец исходной матрицы. Поскольку последний столбец по условию задачи нам известен, добавим его в полученную матрицу

Процесс восстановления

Процесс восстановления Вспомним, что строки матрицы были получены в результате циклического сдвига исходной строки. То есть, символы последнего и первого столбцов образуют друг с другом пары. Отсортируем эти пары, поскольку обязательно существуют такие строки в матрице, которые начинаются с этих пар. Заодно допишем в матрицу и известный нам последний столбец

Процесс восстановления

Пример BWT Пусть нам дана исходная строка s=«ABACABA»

Пример BWT

Преобразование Шиндлера Спустя год после опубликования алгоритма BWT, Михаэлем Шиндлером было предложено альтернативное преобразования данных (частичное сортирующее преобразование ST), являющееся главным образом обобщением BWT

Преобразование Шиндлера Отличие от BWT заключается в том, что строки матрицы перестановок упорядочиваются не по всей длине, а только по указанному количеству первых символов. Число таких символов называется порядком преобразования Шиндлера.

Преобразование Шиндлера В случае, если эти символы одинаковы у двух или более строк, они упорядочиваются в соответствии с номером позиции, в которой эти строки встречаются в исходной последовательности.

Преобразование Шиндлера

Методы, используемые совместно с BWT Само по себе преобразование Барроуза - Уилера не сжимает. Эту работу проделывают другие методы. Среди таких методов можно отметить следующие: кодирование длин повторов (RLE) метод перемещения стопки книг (MTF) кодирование расстояний (DC) метод Хаффмана арифметическое кодирование

Методы, используемые совместно с BWT Последовательность применения методов, используемых совместно с BWT

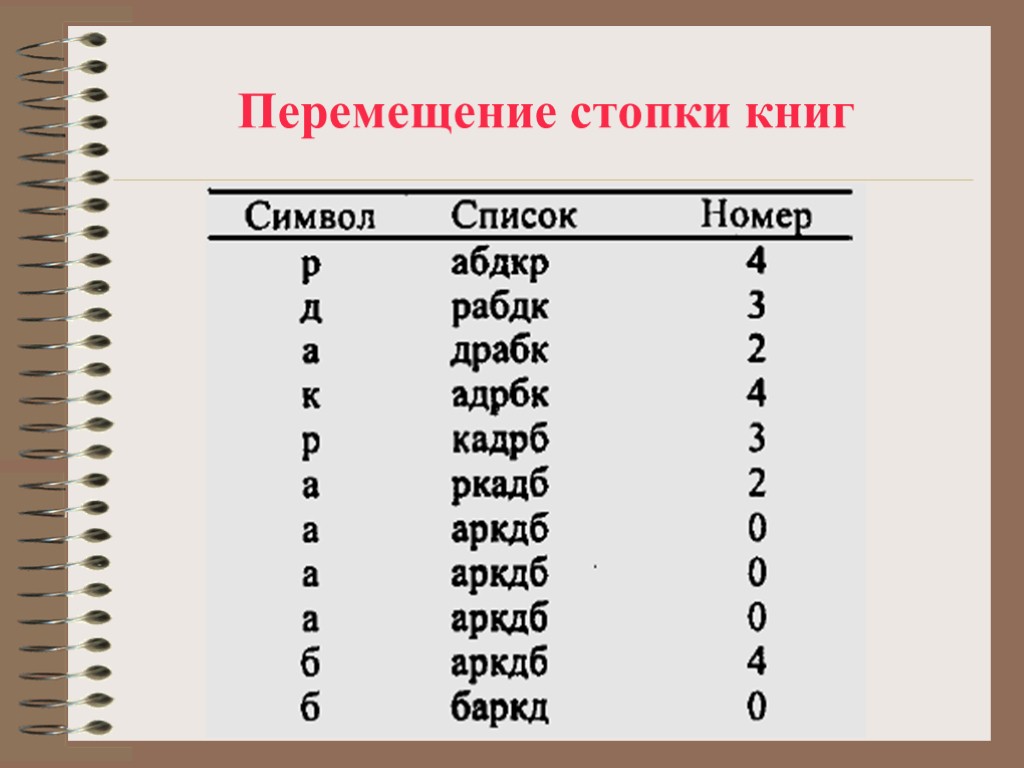
Перемещение стопки книг Метод также известен под названием MTF (Move To Front). Суть его легко понять, если представить процесс перемещения книг в стопке, из которой время от времени достают нужную книгу и кладут сверху. Таким образом, через некоторое время наиболее часто используемые книги оказываются ближе к верхушке стопки.

Перемещение стопки книг Для примера произведем преобразование над последовательностью "рдакраааабб", полученной нами после BWT. Предположим, что мы имеем дело с алфавитом, содержащим только эти 5 символов и в упорядоченном списке символов они расположены в следующем порядке: М = {"а", "б", "д", "к", р"}

Перемещение стопки книг Первый из символов последовательности, "р", находится в списке под номером 4. Это число мы и записываем в выходной блок. Затем мы изменяем список, перенося этот символ в вершину списка, при этом сдвигая все остальные элементы, находившиеся до этого выше. Следующий символ, "д", после этого сдвига оказывается в списке под номером 3. и т. д.

Перемещение стопки книг

Перемещение стопки книг Таким образом, в результате преобразования по методу перемещения стопки книг мы получили последовательность "43243200040".

Перемещение стопки книг Результат после преобразования BWT (рдакраааабб 3) закодируем по методу Хаффмана без MTF и закодируем по методу Хаффмана после работы MTF (43243200040 3). В результате закодированная строка после работы MTF имеет меньший размер, чем без MTF.

Кодирование длин повторов Кодирование длин участков (или повторений) может быть достаточно эффективным при сжатии двоичных данных, например, черно-белых факсимильных изображений, черно-белых изображений, содержащих множество прямых линий и однородных участков, схем и т.п.

Кодирование длин повторов Кодирование длин серий (англ. Run-length encoding, RLE) или Кодирование повторов — простой алгоритм сжатия данных, который оперирует сериями данных, то есть последовательностями, в которых один и тот же символ встречается несколько раз подряд.

Кодирование длин повторов Идея сжатия данных на основе кодирования длин повторений состоит в том, что вместо кодирования собственно данных подвергаются кодированию числа, соответствующие длинам участков, на которых данные сохраняют неизменное значение.

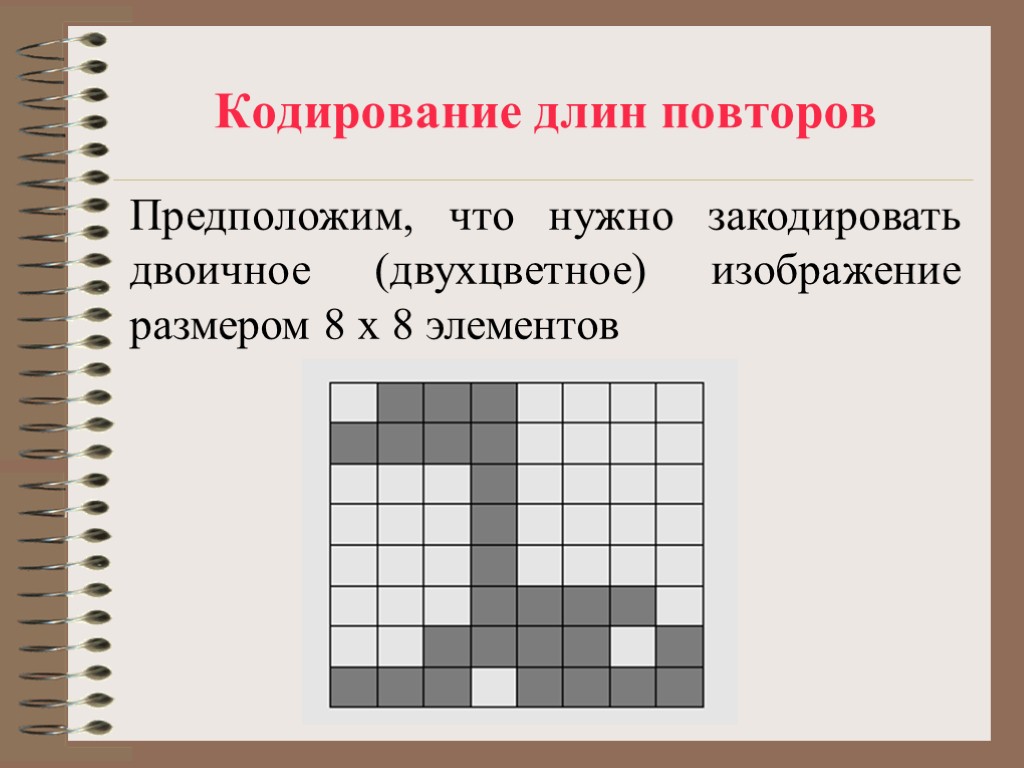
Кодирование длин повторов Предположим, что нужно закодировать двоичное (двухцветное) изображение размером 8 х 8 элементов

Кодирование длин повторов Просканируем это изображение по строкам (двум цветам на изображении будут соответствовать 0 и 1), в результате получим двоичный вектор данных X=(0111000011110000000100000001000000010000000111100011110111101111) Длина 64 бита

Кодирование длин повторов Выделим в векторе X участки, на которых данные сохраняют неизменное значение, и определим их длины. Результирующая последовательность длин участков - положительных целых чисел, соответствующих исходному вектору данных X, - будет иметь вид r = (1, 3, 4, 4, 7, 1, 7, 1, 7, 1, 7, 4, 3, 4, 1, 4, 1, 4)

Кодирование длин повторов При кодировании строка одинаковых символов, составляющих серию, заменяется строкой, которая содержит сам повторяющийся символ и количество его повторов.

Кодирование длин повторов WWWWWWWWWWWWBWWWWWWWWWWWWBBBWWWWWWWWWWWWWWWWWWWWWWWWBWWWWWWWWWWWWWW Если мы применим простое кодирование длин серий к этой строке, то получим следующее: 12W1B12W3B24W1B14W

Кодирование длин повторов Однако, в случае, если строка состоит из большого количества неповторяющихся символов, её объем может вырасти. ABCABCABCABCDDEFFFFFFFF 1A1B1C1A1B1C1A1B1C1A1B1C2D1E8F

Кодирование длин повторов Проблема решается достаточно просто. Алфавит, в котором записаны длины серий, разделяется на две (обычно равные) части. Алфавит целых чисел можно, например, разделить на две части: положительные и отрицательные. Положительные используют для записи количества повторяющихся одинаковых символов, а отрицательные — для записи количества неодинаковых.

Кодирование длин повторов ABCABCABCABCDDEFFFFFFFF -12ABCABCABCABC2D1E8F