Предварительная обработка экспериментальных данных Предварительная обработка опыта

Предварительная обработка экспериментальных данных

Предварительная обработка опыта - отсеивание грубых погрешностей измерения или погрешностей, неизбежно имеющих место при переписывании цифрового материала или при вводе информации; - соответствие распределения результатов измерения закону нормального распределения;

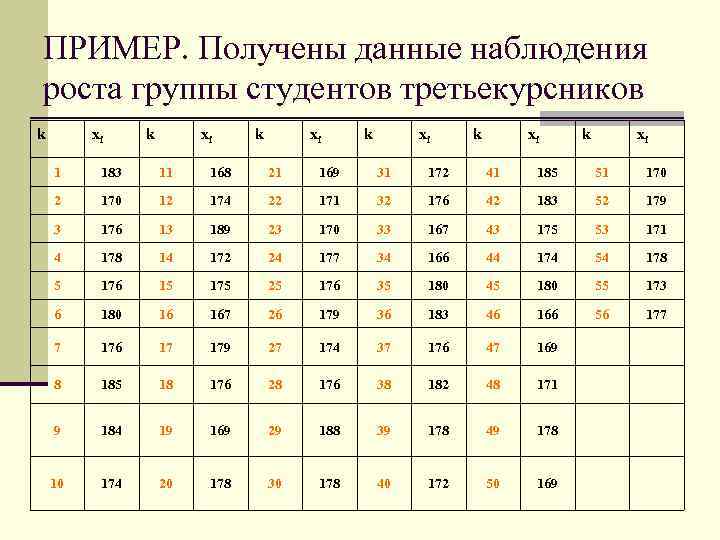
ПРИМЕР. Получены данные наблюдения роста группы студентов третьекурсников k xi k xi 1 183 11 168 21 169 31 172 41 185 51 170 2 170 12 174 22 171 32 176 42 183 52 179 3 176 13 189 23 170 33 167 43 175 53 171 4 178 14 172 24 177 34 166 44 174 54 178 5 176 15 175 25 176 35 180 45 180 55 173 6 180 16 167 26 179 36 183 46 166 56 177 7 176 17 179 27 174 37 176 47 169 8 185 18 176 28 176 38 182 48 171 9 184 19 169 29 188 39 178 49 178 10 174 20 178 30 178 40 172 50 169

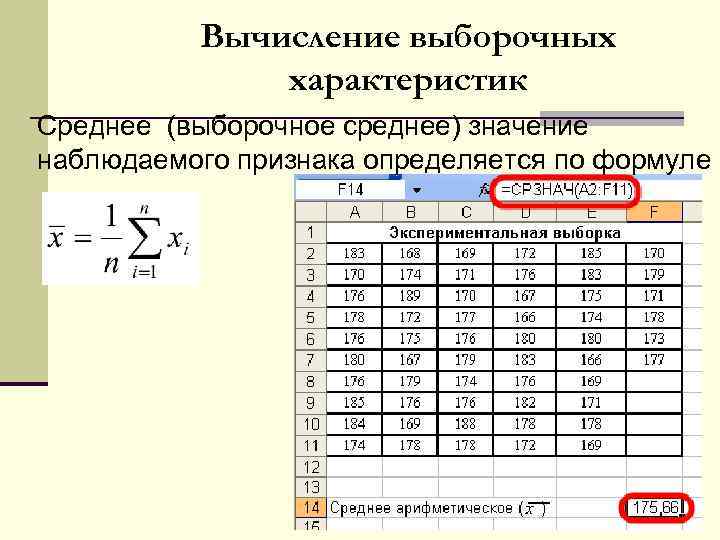
Вычисление выборочных характеристик Среднее (выборочное среднее) значение наблюдаемого признака определяется по формуле

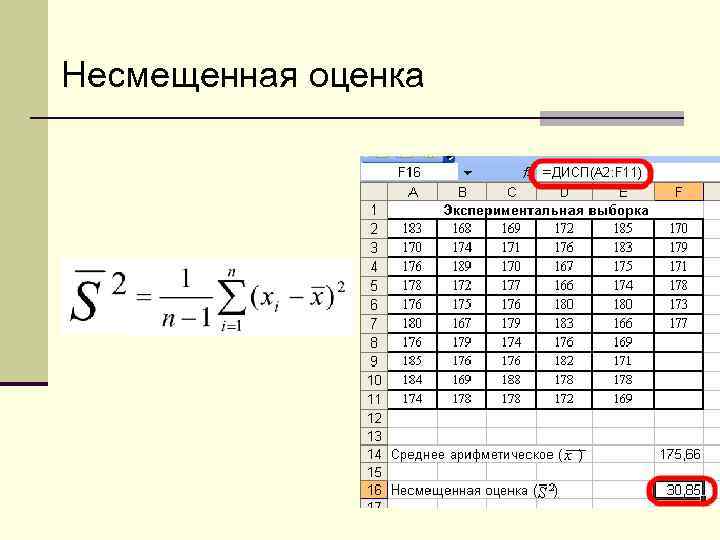
Несмещенная оценка

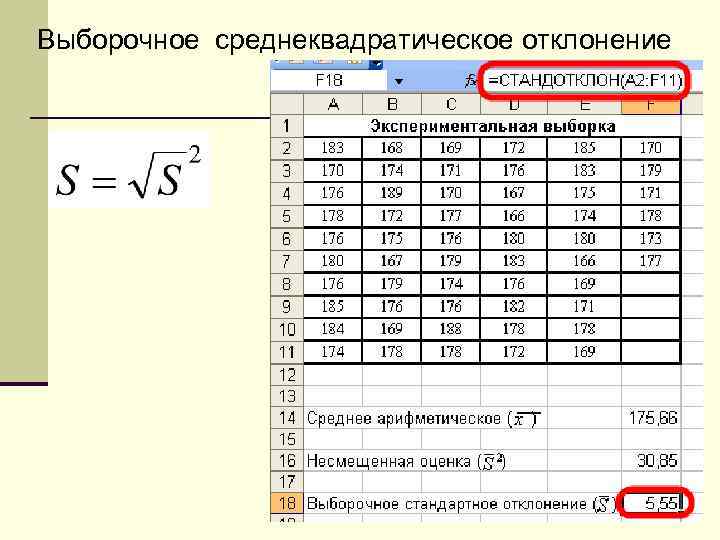
Выборочное среднеквадратическое отклонение

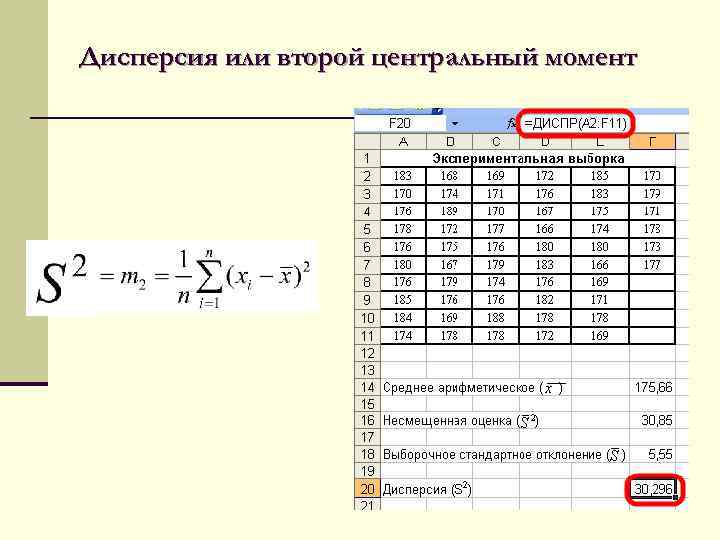
Дисперсия или второй центральный момент

Проверка надежности данных Для того, что бы проверить, являются ли данные и вычисления надежными рассчитывают коэффициент вариации И сопоставляют с его ошибкой Проверяют условие: Т. к. 0, 016<0, 032, то результаты вычислений надежны и количество исходных данных достаточно

Уровни значимости n первый уровень - 5% (р=0, 05); где допускается риск ошибки в выводе в пяти случаях из ста теоретически возможных таких же экспериментов при строго случайном отборе испытуемых для каждого эксперимента; n второй уровень - 1%, т. е. соответственно допускается риск ошибиться только в одном случае из ста; n третий уровень - 0, 1%, т. е. допускается риск ошибиться только в одном случае из тысячи.

Отсев грубых погрешностей выбирают наблюдение, имеющее наибольшее отклонение от среднего 1. 1, 89 -1, 7566=0, 1334 по формуле выделяют аномального значение

по формуле находят по таблице приложений t –распределения Стьюдента (приложение 1) 2, 4 находится между двумя табличными значениями, т. е. от отсева выделяющегося наблюдения лучше отказаться.

Статистическая совокупность и вариационный ряд Разбиение на классы рассчитывают по формуле разница между максимальным и минимальным значением составляет 189 -166=23(см), то число классов примем равным 6 со ступенями равными по 4 см; 6∙ 4=24≈23

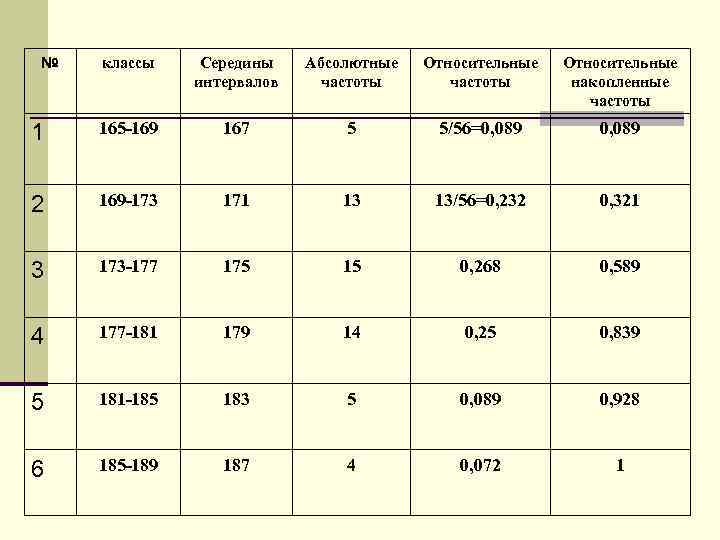
№ классы Середины интервалов Абсолютные частоты Относительные накопленные частоты 1 165 -169 167 5 5/56=0, 089 2 169 -173 171 13 13/56=0, 232 0, 321 3 173 -177 175 15 0, 268 0, 589 4 177 -181 179 14 0, 25 0, 839 5 181 -185 183 5 0, 089 0, 928 6 185 -189 187 4 0, 072 1

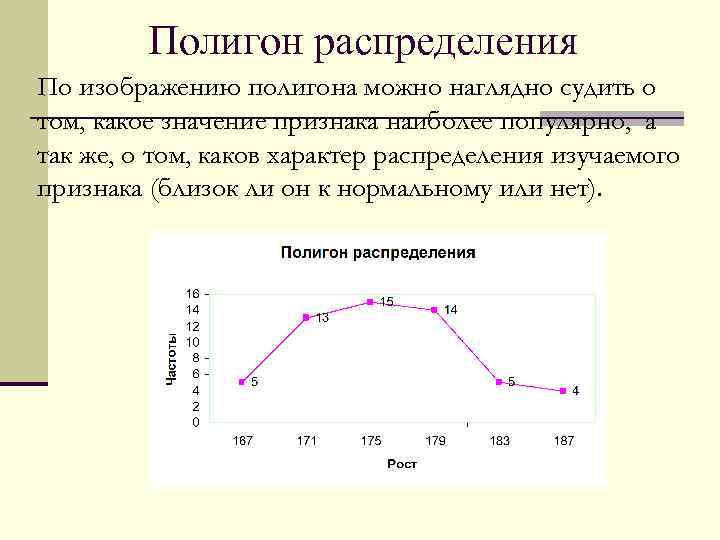
Полигон распределения По изображению полигона можно наглядно судить о том, какое значение признака наиболее популярно, а так же, о том, каков характер распределения изучаемого признака (близок ли он к нормальному или нет).

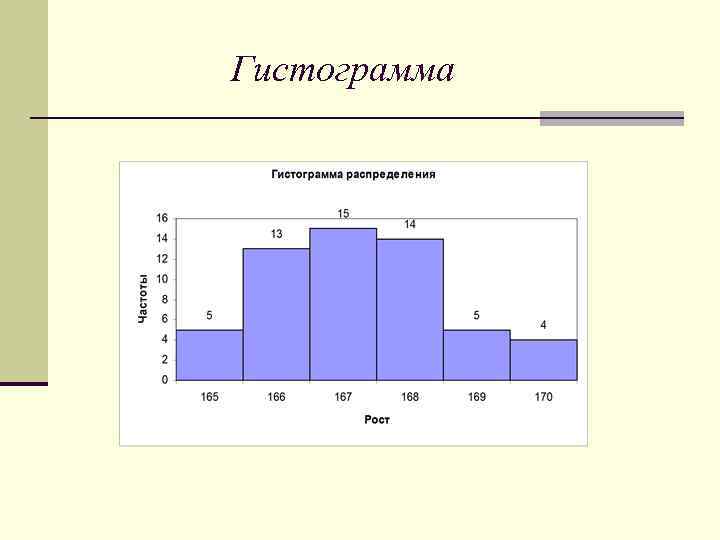
Гистограмма

Проверка гипотезы нормальности распределения Рассмотрим 4 основные методики проверки гипотезы о нормальном распределении: n по среднему абсолютному отклонению (САО), n по размаху варьирования R (быстрая «прикидочная» проверка нормального распределения) n по показателям асимметрии и эксцесса; (иллюстрирует использование моментов удобна при проведении расчетов на ЭВМ) n по критерию хи квадрат (основательная проверка нормальности распределения)

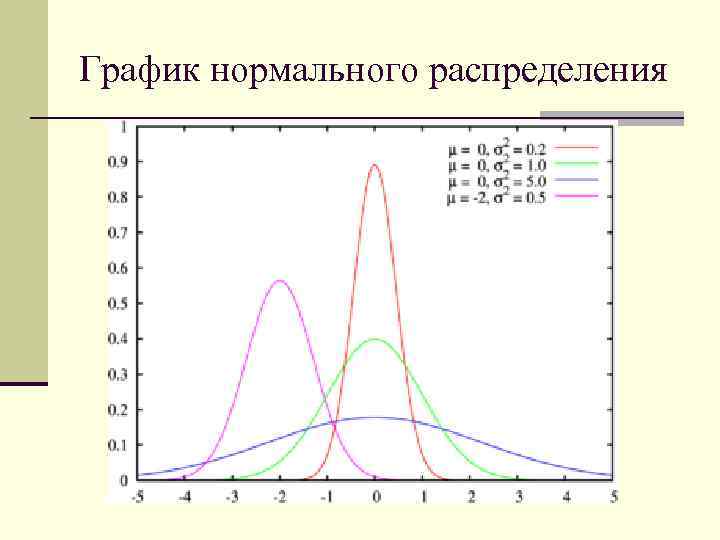
График нормального распределения

По среднему абсолютному отклонению (САО) для выборок n<120 n Найти среднее абсолютное отклонение n Для выборки, имеющий нормальный закон распределения, должно быть справедливо n В нашем случае n Следовательно гипотеза о нормальности распределения выборки данных принимается

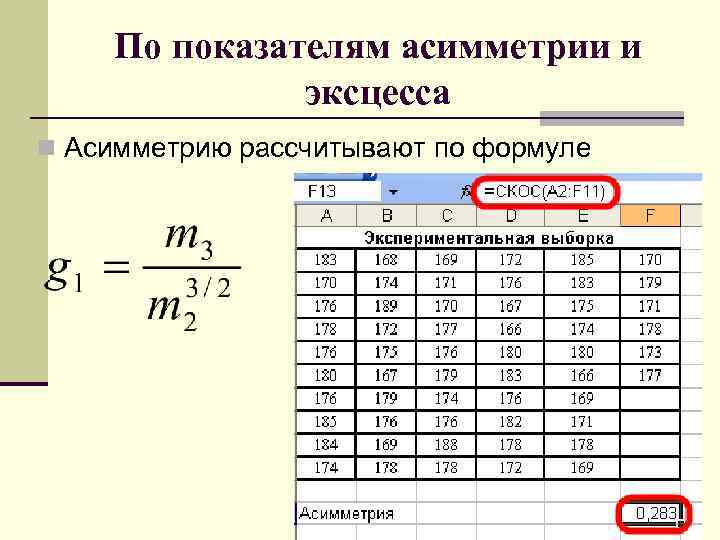
По показателям асимметрии и эксцесса n Асимметрию рассчитывают по формуле

Теоретические моменты

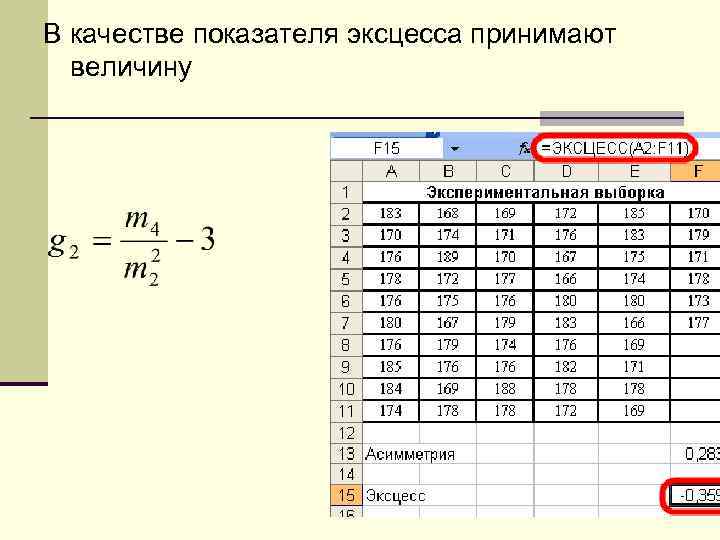
В качестве показателя эксцесса принимают величину

Несмещенные оценки для показателей асимметрии м эксцесса определяются по формулам:

Вычислим среднеквадратические отклонения для показателей асимметрии и эксцесса Проверим условия Т. к 0, 28<0, 96 и 0, 35<3, 15 то гипотеза о нормальности распределения принимается

По размаху варьирования R Для выборок 3<n<1000 Найдем отношение n сопоставим его с критическими верхними и нижними границами (таблица приложений 2) особенно важно, что бы это соблюдалась на 10% уровне значимости. n При n=56 и р=0, 1 4, 03<4, 144<5, 33. Следовательно, гипотеза о нормальности распределения подтверждается

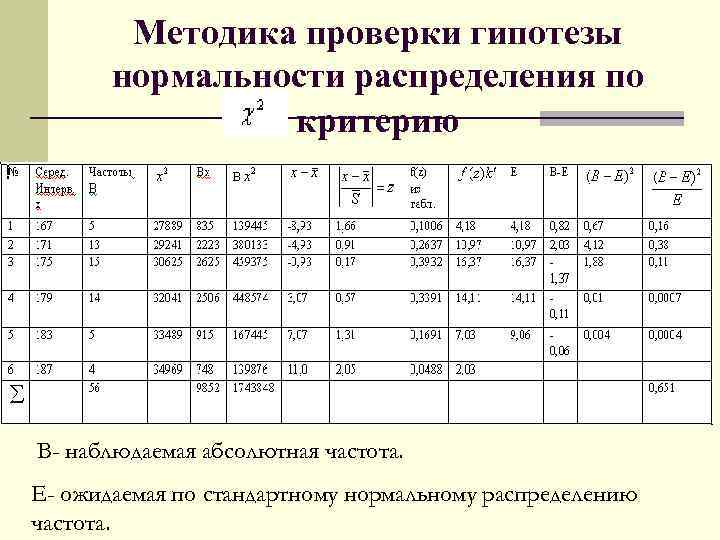
Методика проверки гипотезы нормальности распределения по критерию В- наблюдаемая абсолютная частота. Е- ожидаемая по стандартному нормальному распределению частота.

При расчете данного критерия в Excel предварительно рассчитывают ожидаемый интервал по формулам: 1. 2. Находят f(z) по таблице приложений 3 3. Вычисляют , где

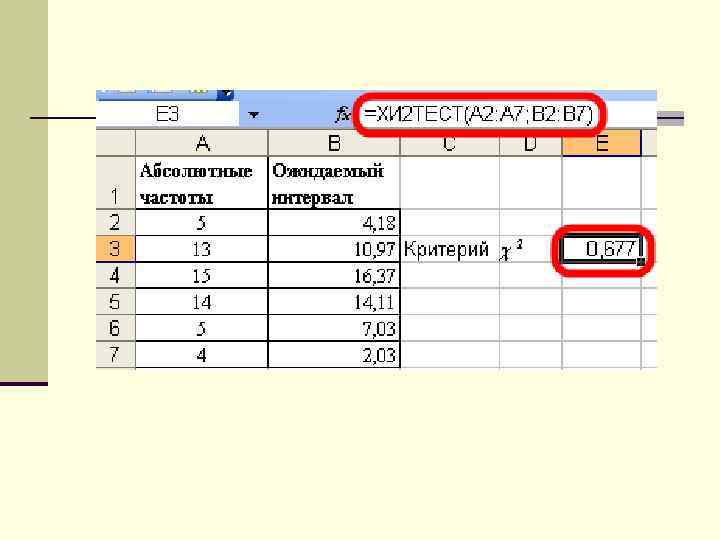
По таблице приложений распределения Получим, Т. е. гипотезу о нормальном распределении принимаем

Логнормальное распределение

Преобразование распределений к нормальному Для распределений имеющих крутую левую ветвь гистограммы и пологую правую, выполняют преобразование матрицы исходных данных по формулам: После каждого преобразования реализуют процедуру вычисления хи квадрат и окончательно принимают то преобразование которое дает минимальное.

Для распределений смещенных вправо матрицу исходных данных преобразуют по формуле (при а=1, 5; 2) и после каждого преобразования реализуют процедуру вычисления. Для принятия гипотезы нормальности преобразованного распределения должно соблюдаться условие