1 Обработка данных=.ppt
- Количество слайдов: 15

Предварительная обработка экспериментальных данных

Постановка задачи Имеется ряд наблюдений x 1, x 2, …, xn Требуется провести предварительную обработку данных. Вычислим выборочное среднее и исправленную выборочную дисперсию № 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 x x-xср (x-xср)2 №п/п 183 170 176 178 176 180 176 185 184 174 168 174 189 172 175 167 179 176 169 178 169 171 170 177 176 179 174 176 188 178 7, 34 -5, 66 0, 34 2, 34 0, 34 4, 34 0, 34 9, 34 8, 34 -1, 66 -7, 66 -1, 66 13, 34 -3, 66 -0, 66 -8, 66 3, 34 0, 34 -6, 66 2, 34 -6, 66 -4, 66 -5, 66 1, 34 0, 34 3, 34 -1, 66 0, 34 12, 34 53, 88 32, 04 0, 12 5, 48 0, 12 18, 84 0, 12 87, 23 69, 56 2, 75 58, 68 2, 75 177, 95 13, 39 0, 43 74, 99 11, 16 0, 12 44, 35 5, 48 44, 35 21, 72 32, 04 1, 79 0, 12 11, 16 2, 75 0, 12 152, 27 5, 48 x x-xср (x-xср)2 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 172 176 167 166 180 183 176 182 178 172 185 183 175 174 180 166 169 171 178 169 170 179 171 178 173 177 -3, 66 0, 34 -8, 66 -9, 66 4, 34 7, 34 0, 34 6, 34 2, 34 -3, 66 9, 34 7, 34 -0, 66 -1, 66 4, 34 -9, 66 -6, 66 -4, 66 2, 34 -6, 66 -5, 66 3, 34 -4, 66 2, 34 -2, 66 1, 34 13, 40 0, 12 74, 99 93, 32 18, 84 53, 88 0, 12 40, 19 5, 48 13, 40 87, 23 53, 88 0, 43 2, 75 18, 84 93, 32 44, 36 21, 71 5, 48 44, 36 32, 04 11, 16 21, 72 5, 48 7, 07 1, 79 ∑ 9837 0, 04 1695, 90

Выборочные характеристики распределения Произвольный момент порядка к при , момент называют центральным. Начальным (с = 0) моментом первого порядка является выборочное среднее Несмещенная оценка для Выборочные среднеквадратические отклонения Из других моментов чаще всего используются моменты третьего и четвертого порядка Выборочное значение коэффициента вариации или в процентах Xср S Sср m 1 m 2 m 3 m 4 v% 175, 66 5, 50 5, 55 +0, 04 30, 28 45, 14 2356, 27 3, 00

Разбиение на классы по правилу Штюргеса По правилу Штюргеса число классов вычисляется по формуле: В нашем случае k = 1 + 3. 32 * 1. 75 = 6. 81 Разница между Xmax и Xmin (размах варьирования) составляет 189 – 166 = 23. Исходя из этого, примем число классов разбиения 6. № Классы Середины интервалов Частоты абсолютные относительные 1 2 3 4 5 6 От 165 до 169 От 169 до 173 От 173 до 177 От 177 до 181 От 181 до 185 От 185 до 189 167 171 175 179 183 187 5 13 15 14 5 4 0, 089 0, 232 0, 268 0, 250 0, 089 0, 072 относительные накопительные 0, 089 0, 321 0, 589 0, 839 0, 928 1, 00
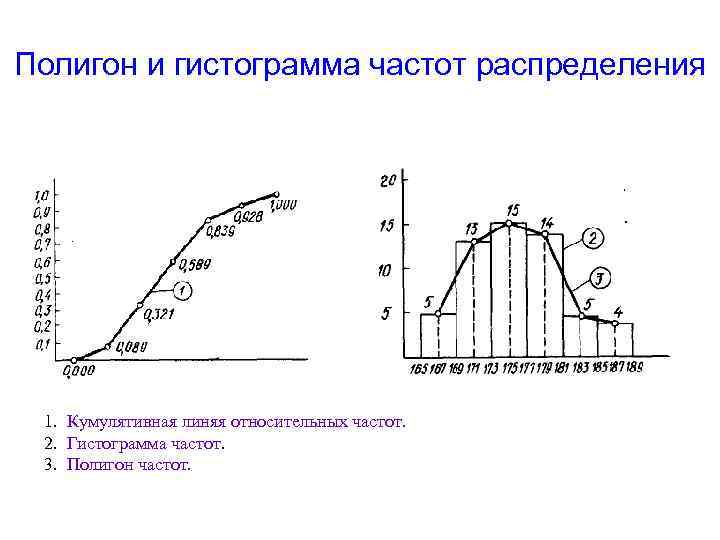
Полигон и гистограмма частот распределения 1. Кумулятивная линяя относительных частот. 2. Гистограмма частот. 3. Полигон частот.

Отсев грубых погрешностей Если п < 25, используют метод вычисления максимального относительного отклонения где τ(p, n) - табличное значение. Если неравенство неверно, то варианта, на которой достигается максимум, отсеивается. Для больших выборок при вычислении τ(p, n) используют критическое значение распределения Стьюдента t(p, n-2) В рассматриваемом примере 1) Выберем наблюдение с наибольшим отклонением: 189 2) по таблице процентных точек распределения Стьюдента найдем t(5%, 54) = 1. 6735, t(0. 1%, 54) = 3. 2574; 3) Вычислим соответствующие значения τ(5%, 56) = 1. 647, τ(0. 1%, 54) = 3. 005 Максимальное относительное отклонение τ = 2, 40 находится между двумя табличными критическими значениями: 1, 647 < 2, 40 < 3, 005. В этом случае отсев не делается.

Проверка нормальности по САО и размаху варьирования Для небольших выборок (n < 120) вычисляется среднее абсолютное отклонение (САО) по формуле и проверяется справедливость неравенства САО = 247/56 = 4, 41. Подставим это значение в формулу: |4, 41/5, 55 - 0, 7979| < 0, 4/√ 56; т. е. 0, 0032 < 0, 0535. Гипотеза нормальности распределения выборки принимается. Для выборок 3 < п < 1000 можно использовать размах варьирования R. Если отношение R/S меньше нижней или больше верхней критических границ отношения , (Таблица) то распределения не согласовано с нормальным. В примере R/S = 23/5, 55 = 4, 144. При п = 56 и р = 0, 10 нижняя и верхняя границы по соответственно равны 4, 03 и 5, 23, т. е. 4, 03 < 4, 144 < 5, 23. Следовательно, гипотеза нормальности распределения подтверждается и по этому критерию.

Проверка на нормальность с помощью асимметрии и эксцесса Показатель асимметрии можно определить по формуле Следовательно, некоторая асимметрия имеет место. Имеется также и небольшой эксцесс. Несмещенные оценки для показателей асимметрии и эксцесса определяют по формулам Для проверки гипотезы нормальности распределения следует также вычислить среднеквадратические отклонения для показателей асимметрии и эксцесса: Если выполняются неравенства то гипотеза нормальности исследуемого распределения может быть принята. В данном примере 0, 28 < 0, 96 и 0, 35 <3, 15; следовательно, гипотеза нормальности распределения может быть принята.
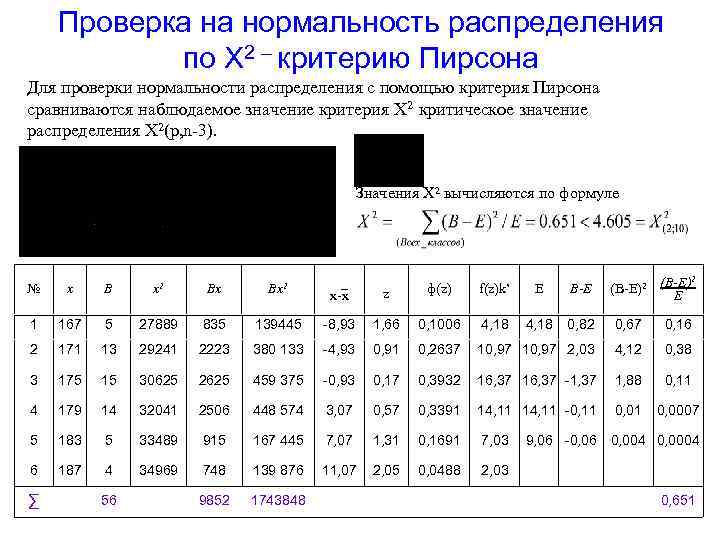
Проверка на нормальность распределения по X 2 – критерию Пирсона Для проверки нормальности распределения с помощью критерия Пирсона сравниваются наблюдаемое значение критерия X 2 критическое значение распределения X 2(p, n-3). Значения X 2 вычисляются по формуле № х В х2 Вх Вх2 _ x-x 1 167 5 27889 835 139445 2 171 13 29241 2223 3 175 15 30625 4 179 14 5 183 6 187 ∑ 2 (B-E)2 (В-Е) E z ф(z) f(z)k’ E В-Е -8, 93 1, 66 0, 1006 4, 18 0, 82 0, 67 0, 16 380 133 -4, 93 0, 91 0, 2637 10, 97 2, 03 4, 12 0, 38 2625 459 375 -0, 93 0, 17 0, 3932 16, 37 -1, 37 1, 88 0, 11 32041 2506 448 574 3, 07 0, 57 0, 3391 14, 11 -0, 11 0, 0007 5 33489 915 167 445 7, 07 1, 31 0, 1691 7, 03 4 34969 748 139 876 11, 07 2, 05 0, 0488 2, 03 9852 1743848 56 9, 06 -0, 06 0, 004 0, 0004 0, 651

Проверки нормальности распределения с помощью критерия Колмогорова-Смирнова Для проверки нормальности распределения с помощью критерия Колмогорова. Смирнова нужно вычислить где FB — накопленная наблюдаемая частота; FE — накопленная ожидаемая частота. FB и FE получены накоплением частот В и Е. Затем выбирают максимальное значение FB - FE и по нему определяют критерий согласия Колмогорова- Смирнова D. Полученное значение сравнивают с критическим DТ из таблицы. Получим DТ(56; 0. 10) = 0, 167 > 0, 05 = D, т. е. гипотеза нормального распределения на достаточно «жестком» 10%-ном уровне принимается. B 5 13 15 14 5 4 E 4, 18 10, 97 16, 37 14, 11 7, 03 2, 03 FB 5 18 33 47 52 56 FE 4, 18 15, 15 31, 52 45, 63 52, 66 54, 69 |FB-FE| 0, 82 2, 85 1, 48 1, 37 0, 66 1, 31

Блок-схема алгоритма предварительной обработки данных Проверка нормальности выборки Отсев грубых ошибок Ввод исходных данных xk Вычисление выбор. характеристик τ <τ(5%, n) τ <τ(0. 1%, n) нет Отсев грубой ошибки N = N-1 Вычисление G 1, G 2, SG 1, SG 2, X 2, D υ% < 33 да Грубые проверки нормальности нет Преобразование выборки да Проверка критериев X 2, К-С согласована Завершение предварительной обработки данных
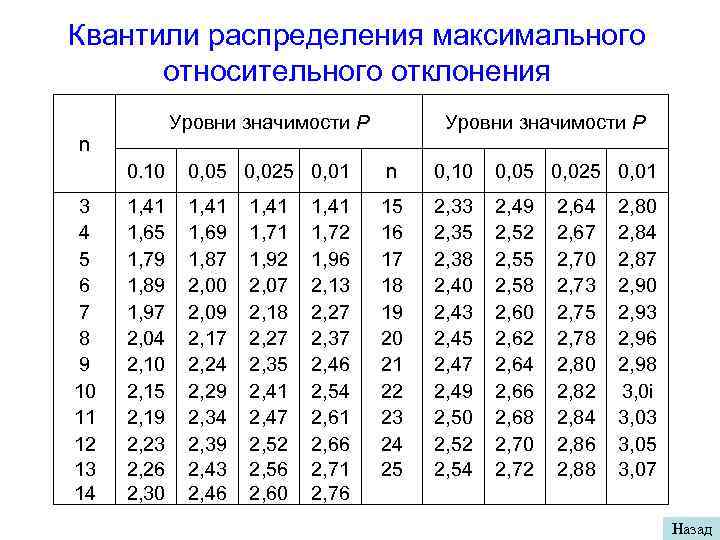
Квантили распределения максимального относительного отклонения Уровни значимости Р n Уровни значимости Р 0. 10 3 4 5 6 7 8 9 10 11 12 13 14 0, 05 0, 025 0, 01 n 0, 10 0, 05 0, 025 0, 01 1, 41 1, 65 1, 79 1, 89 1, 97 2, 04 2, 10 2, 15 2, 19 2, 23 2, 26 2, 30 1, 41 1, 69 1, 87 2, 00 2, 09 2, 17 2, 24 2, 29 2, 34 2, 39 2, 43 2, 46 15 16 17 18 19 20 21 22 23 24 25 2, 33 2, 35 2, 38 2, 40 2, 43 2, 45 2, 47 2, 49 2, 50 2, 52 2, 54 2, 49 2, 52 2, 55 2, 58 2, 60 2, 62 2, 64 2, 66 2, 68 2, 70 2, 72 1, 41 1, 71 1, 92 2, 07 2, 18 2, 27 2, 35 2, 41 2, 47 2, 52 2, 56 2, 60 1, 41 1, 72 1, 96 2, 13 2, 27 2, 37 2, 46 2, 54 2, 61 2, 66 2, 71 2, 76 2, 64 2, 67 2, 70 2, 73 2, 75 2, 78 2, 80 2, 82 2, 84 2, 86 2, 88 2, 80 2, 84 2, 87 2, 90 2, 93 2, 96 2, 98 3, 0 i 3, 03 3, 05 3, 07 Назад
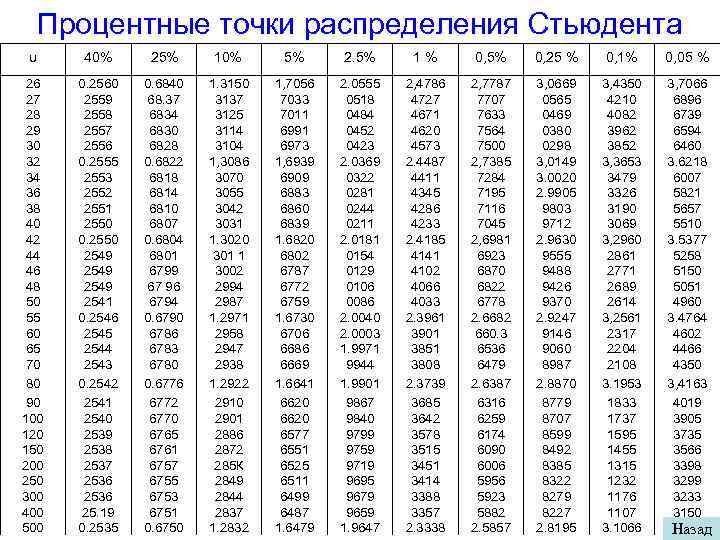
Процентные точки распределения Стьюдента υ 40% 25% 10% 5% 2. 5% 1% 0, 5% 0, 25 % 0, 1% 0, 05 % 26 27 28 29 30 32 34 36 38 40 42 44 46 48 50 55 60 65 70 80 90 100 120 150 200 250 300 400 500 0. 2560 2559 2558 2557 2556 0. 2555 2553 2552 2551 2550 0. 2550 2549 2541 0. 2546 2545 2544 2543 0. 2542 2541 2540 2539 2538 2537 2536 25. 19 0. 2535 0. 6840 68. 37 6834 6830 6828 0. 6822 6818 6814 6810 6807 0. 6804 6801 6799 67 96 6794 0. 6790 6786 6783 6780 0. 6776 6772 6770 6765 6761 6757 6755 6753 6751 0. 6750 1. 3150 3137 3125 3114 3104 1, 3086 3070 3055 3042 3031 1. 3020 301 1 3002 2994 2987 1. 2971 2958 2947 2938 1. 2922 2910 2901 2886 2872 285 К 2849 2844 2837 1. 2832 1, 7056 7033 7011 6991 6973 1, 6939 6909 6883 6860 6839 1. 6820 6802 6787 6772 6759 1. 6730 6706 6686 6669 1. 6641 6620 6577 6551 6525 6511 6499 6487 1. 6479 2. 0555 0518 0484 0452 0423 2. 0369 0322 0281 0244 0211 2. 0181 0154 0129 0106 0086 2. 0040 2. 0003 1. 9971 9944 1. 9901 9867 9840 9799 9759 9719 9695 9679 9659 1. 9647 2, 4786 4727 4671 4620 4573 2. 4487 4411 4345 4286 4233 2. 4185 4141 4102 4066 4033 2. 3961 3901 3851 3808 2. 3739 3685 3642 3578 3515 3451 3414 3388 3357 2. 3338 2, 7787 7707 7633 7564 7500 2, 7385 7284 7195 7116 7045 2, 6981 6923 6870 6822 6778 2. 6682 660. 3 6536 6479 2. 6387 6316 6259 6174 6090 6006 5956 5923 5882 2. 5857 3, 0669 0565 0469 0380 0298 3, 0149 3. 0020 2. 9905 9803 9712 2. 9630 9555 9488 9426 9370 2. 9247 9146 9060 8987 2. 8870 8779 8707 8599 8492 8385 8322 8279 8227 2. 8195 3, 4350 4210 4082 3962 3852 3, 3653 3479 3326 3190 3069 3, 2960 2861 2771 2689 2614 3, 2561 2317 2204 2108 3. 1953 1833 1737 1595 1455 1315 1232 1176 1107 3. 1066 3, 7066 6896 6739 6594 6460 3. 6218 6007 5821 5657 5510 3. 5377 5258 5150 5051 4960 3. 4764 4602 4466 4350 3, 4163 4019 3905 3735 3566 3398 3299 3233 3150 3. 3101 Назад
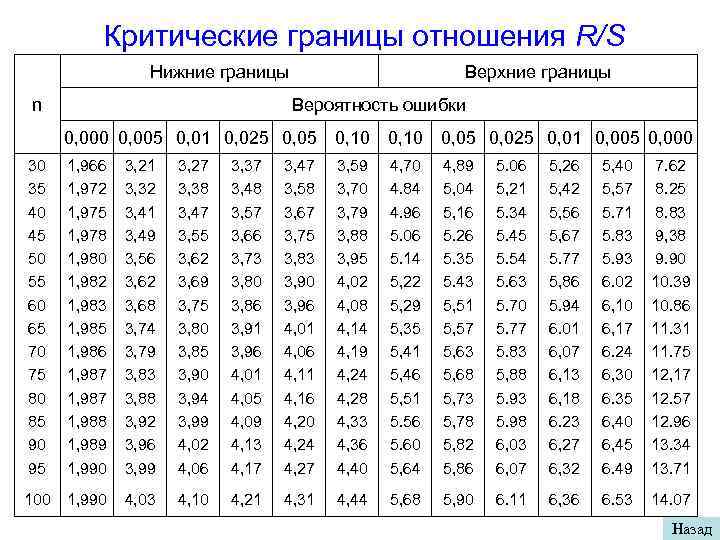
Критические границы отношения R/S Нижние границы n Верхние границы Вероятность ошибки 0, 000 0, 005 0, 01 0, 025 0, 05 0, 10 0, 05 0, 025 0, 01 0, 005 0, 000 30 35 40 45 50 55 60 65 70 75 80 85 90 1, 966 1, 972 1, 975 1, 978 1, 980 1, 982 1, 983 1, 985 1, 986 1, 987 1, 988 1, 989 3, 21 3, 32 3, 41 3, 49 3, 56 3, 62 3, 68 3, 74 3, 79 3, 83 3, 88 3, 92 3, 96 3, 27 3, 38 3, 47 3, 55 3, 62 3, 69 3, 75 3, 80 3, 85 3, 90 3, 94 3, 99 4, 02 3, 37 3, 48 3, 57 3, 66 3, 73 3, 80 3, 86 3, 91 3, 96 4, 01 4, 05 4, 09 4, 13 3, 47 3, 58 3, 67 3, 75 3, 83 3, 90 3, 96 4, 01 4, 06 4, 11 4, 16 4, 20 4, 24 3, 59 3, 70 3, 79 3, 88 3, 95 4, 02 4, 08 4, 14 4, 19 4, 24 4, 28 4, 33 4, 36 4, 70 4. 84 4. 96 5. 06 5. 14 5, 22 5, 29 5, 35 5, 41 5, 46 5, 51 5. 56 5. 60 4, 89 5, 04 5, 16 5. 26 5. 35 5. 43 5, 51 5, 57 5, 63 5, 68 5, 73 5, 78 5, 82 5. 06 5, 21 5. 34 5. 45 5. 54 5. 63 5. 70 5. 77 5. 83 5, 88 5. 93 5. 98 6, 03 5, 26 5, 42 5, 56 5, 67 5. 77 5, 86 5. 94 6. 01 6, 07 6, 13 6, 18 6. 23 6, 27 5, 40 5, 57 5. 71 5. 83 5. 93 6. 02 6, 10 6, 17 6. 24 6, 30 6. 35 6, 40 6, 45 7. 62 8. 25 8. 83 9, 38 9. 90 10. 39 10. 86 11. 31 11. 75 12, 17 12. 57 12. 96 13. 34 95 1, 990 3, 99 4, 06 4, 17 4, 27 4, 40 5, 64 5, 86 6, 07 6, 32 6. 49 13. 71 100 1, 990 4, 03 4, 10 4, 21 4, 31 4, 44 5, 68 5, 90 6. 11 6, 36 6. 53 14. 07 Назад

Критические значения К-С - критерия n D 0, 10 D 0, 05 3 4 5 б 7 8 9 10 11 12 13 14 15 16 0, 636 0, 565 0, 509 0, 468 0, 436 0, 410 0, 387 0, 369 0, 352 0, 338 0, 325 0, 314 0, 304 0, 295 0, 708 0, 624 0, 563 0, 519 0, 483 0, 454 0, 430 0, 409 0, 391 0 -. 375 0, 361 0, 349 0, 338 0, 327 17 18 19 20 21 22 23 24 25 26 27 28 29 30 0, 286 0, 278 0, 271 0, 265 0, 259 0, 253 0, 247 0, 242 0, 238 0, 233 0, 229 0, 225 0, 221 0, 218 0, 309 0, 301 0, 294 0, 287 0, 281 0, 275 0, 269 0, 264 0, 259 0, 254 0, 250 0, 246 0, 242 31 32 33 34 35 36 37 38 39 40 50 100 0, 214 0, 211 0, 208 0, 205 0, 202 0, 199 0, 196 0, 194 0, 191 0, 189 0, 170 0, 121 0, 238 0, 234 0, 231 0, 227 0, 224 0, 221 0, 218 0, 215 0, 213 0, 210 0, 177 0, 134 Назад
1 Обработка данных=.ppt