Представление графов и отношений Граф G

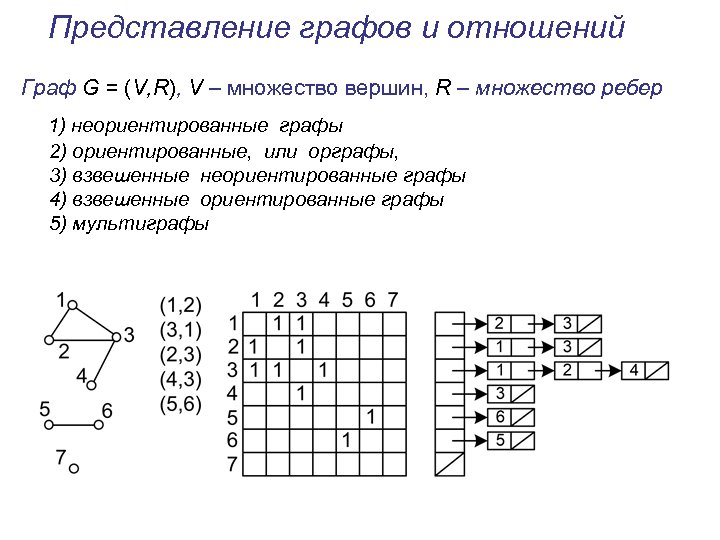Представление графов и отношений Граф G = (V, R), V – множество вершин, R – множество ребер 1) неориентированные графы 2) ориентированные, или орграфы, 3) взвешенные неориентированные графы 4) взвешенные ориентированные графы 5) мультиграфы

Формирование списков, задающих граф Вершины графа – номера от 1 до n. Число ребер - m. Ребро графа – два номера вершин (p, q). i-е ребро – (v 1[i], v 2[i]). ____________________ for k: =1 to n do S[k]: =nil; {обнуление указателей} for i: =1 to m do {формирование списков} begin new(ps); ps^. s: =v 2[i]; k: =v 1[i]; ps^. p: =S[k]; S[k]: =ps; {формирование 2 -го элемента для неор. графа: } new(ps); ps^. s: =v 1[i]; k: =v 2[i]; ps^. p: =S[k]; S[k]: =ps end;

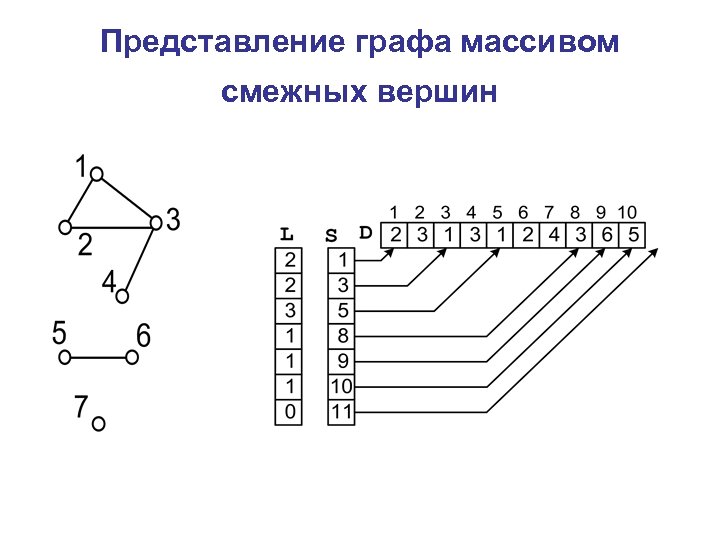Представление графа массивом смежных вершин

Формирование массивов D, S и L для задания неориентированного графа for j: =1 to n do L[j]: =0; {обнуление длин списков} for i: =1 to m do begin {вычисление длин списков} k: =v 1[i]; L[k]: =L[k]+1; k: =v 2[i]; L[k]: =L[k]+1; end; S[1]: =1; {вычисление указателей на начала списков в массиве D} for j: =2 to n do S[j]: =S[j-1]+L[j-1]; for j: =1 to n do {дублирование указателей} U[j]: =S[j]; for i: =1 to m do {распределение смежных вершин} begin {по спискам массива D} k: =v 1[i]; D[U[k]]: =v 2[i]; U[k]: =U[k]+1 k: =v 2[i]; D[U[k]]: =v 1[i]; U[k]: =U[k]+1 end;

Просмотр неориентированного графа вглубь Массив R для нумерации вершин графа по порядку просмотра. Если i–я вершина при просмотре была j–й, то R[i]=j. ___________________________________ procedure deеp(k: integer); var i: integer; begin for i: =1 to n do if (M[k, i]=1)and(R[i]=0) then begin nom: =nom+1; R[i]: =nom; deеp(i) end; ___________________________________ for i: =1 to n do R[i]: =0; R[a]: =1; nom: =1; deеp(a); {просмотр, начиная с вершины номер a}

Выделение компонент связности графа for i: =1 to n do C[i]: =0; q: =0; for i: =1 to n do if C[i]=0 then begin q: =q+1; C[i]: =q; cdeеp(i) end; ____________ procedure cdeеp(k: integer); var i: integer; begin for i: =S[k] to S[k]+L[k]-1 do begin j: =D[i]; if C[j]=0 then begin C[j]: =q; cdeеp(j) end end;

Просмотр неориентированного графа вширь для массива смежных вершин V - уровни просмотренных вершин P – номера просмотренных вершин (очередь) _____________________ P[1]: =1; r: =1; t: =1; {очередь из одной вершины} for i: =1 to n do V[i]: =0; V[1]: =1; {уровень для первой вершины} while t<=r do begin k: =P[t]; q: =V[k]+1; for i: =S[k] to S[k]+L[k]-1 do begin j: =D[i]; if V[j]=0 then begin V[j]: =q; r: =r+1; P[r]: =j end; t: =t+1 end;

Просмотр неориентированного графа вширь для матрицы смежности V - уровни просмотренных вершин P – номера просмотренных вершин (очередь) _____________________ P[1]: =1; r: =1; t: =1; {очередь из одной вершины} for i: =1 to n do V[i]: =0; V[1]: =1; {уровень для первой вершины} while t<=r do begin k: =P[t]; q: =V[k]+1; for i: = 1 to n do if (M[k, i]=1)and(V[i]=0) then begin V[i]: =q; r: =r+1; P[r]: =i end; t: =t+1 end;

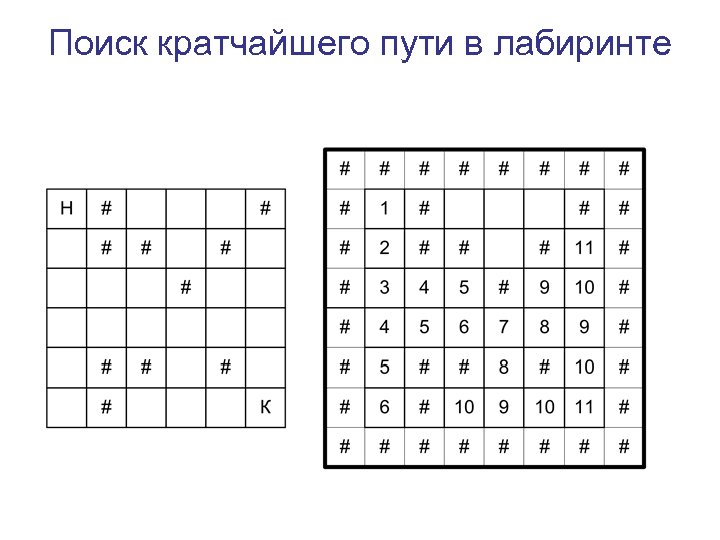Поиск кратчайшего пути в лабиринте

Pi[1]: =i 0; Pj[1]: =j 0; r: =1; t: =1; L[i 0, j 0]: =1; while t<=r do begin i: =Pi[t]; j: =Pj[t]; q: =L[i, j]+1; if L[i-1, j]=0 then begin L[i-1, j]: =q; r: =r+1; Pi[r]: =i-1; Pj[r]: =j end; if L[i, j-1]=0 then begin L[i, j-1]: =q; r: =r+1; Pi[r]: =i; Pj[r]: =j-1 end; if L[i+1, j]=0 then begin L[i+1, j]: =q; r: =r+1; Pi[r]: =i+1; Pj[r]: =j end; if L[i, j+1]=0 then begin L[i, j+1]: =q; r: =r+1; Pi[r]: =i; Pj[r]: =j+1 end; t: =t+1 end;

Отслеживание кратчайшего пути в лабиринте k: =L[ik, jk]; i: =ik; j: =jk; while k>0 do begin Mi[k]: =i; Mj[k]: =j; if L[i-1, j]

Поиск кратчайшего пути в лабиринте алгоритмом бэктрекинга procedure Lab(i, j, k: integer); begin if (i=ik)and(j=jk) then begin kmin: =k; {ЗАПОМНИТЬ МАРШРУТ} end else if k

Вызов процедуры поиска кратчайшего пути в лабиринте kmin: ={∞}; L[i 0, j 0]: =1; Pi[1]: =i 0; Pj[1]: =j 0; Lab(i 0, j 0, 2); Трудоемкость: T (k) ≤ 3 + 32 + 33 +. . . + 3 k = 3(3 k – 1)/2, где k – длина пути, k < n 2.

Эйлеров цикл Количество ребер, входящих во все вершины (для орграфа): for i: =1 to n do R[i]: =0; for i: =1 to n do for k: =S[i] to S[i]+L[i]-1 do begin j: =D[k]; R[j]: =R[j]+1 end Проверка существования эйлерова цикла (для орграфа) : p: =1; for i: =1 to n do if R[i]<>L[i] then p: =0; if p=1 then СУЩЕСТВУЕТ else НЕ СУЩЕСТВУЕТ;

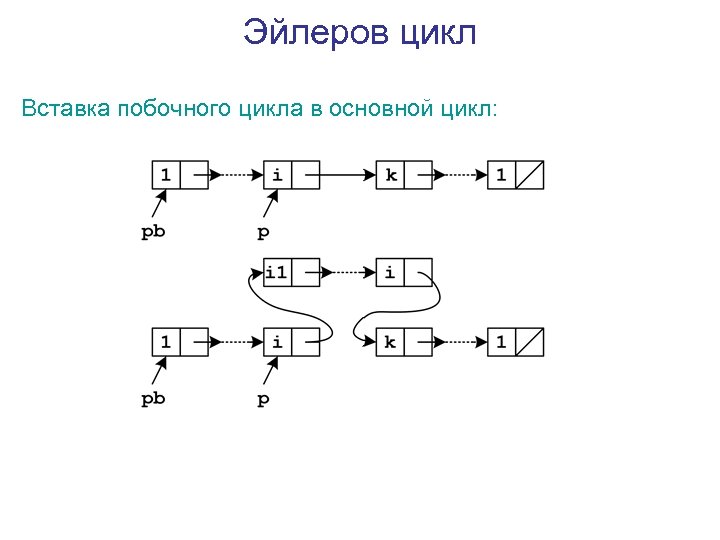Эйлеров цикл Вставка побочного цикла в основной цикл:

Вычисление эйлерова цикла в орграфе для массива смежных вершин new(p); pb: =p; p^. s: =1; p^. p: =nil; while p<>nil do begin if L[p^. s]>0 then begin p 1: =p^. p; i 0: =p^. s; i: =0; p 0: =p; while i<>i 0 do begin new(p 2); p^. p: =p 2; i: =p^. s; i 1: =D[S[i]]; S[i]: =S[i]+1; L[i]: =L[i]-1; i: =i 1; p 2^. s: =i; p: =p 2 end; p^. p: =p 1; p: =p 0 end else p: =p^. p end;

Существование эйлерова цикла в орграфе для матрицы смежности количество ребер, выходящих из всех вершин: for i: =1 to n do begin L[i]: =0; for j: =1 to n do if M[i, j]=1 then L[i]: =L[i]+1 end; количество ребер, входящих во все вершины: for j: =1 to n do begin R[j]: =0; for i: =1 to n do if M[i, j]=1 then R[j]: =R[j]+1 end; Проверка существования эйлерова цикла: p: =1; for i: =1 to n do if R[i]<>L[i] then p: =0; if p=1 then СУЩЕСТВУЕТ else НЕ СУЩЕСТВУЕТ;

Вычисление эйлерова пути в орграфе 1. Вычисление количества ребер, входящих в вершины. 2. Нахождение вершины ib – начала пути, и вершины ik – конца пути. 3. Построение какого-либо пути из вершины ib в вершину ik. После этого во всех вершинах останется по одинаковому числу исходящих и входящих дуг. 4. Построение полного пути добавлением боковых циклов.

Вычисление начального пути в орграфе new(p); pb: =p; p^. s: =ib; i: =ib; while L[i]>0 do begin new(p 1); p^. p: =p 1; i 1: =D[S[i]]; S[i]: =S[i]+1; L[i]: =L[i]-1; p 1^. s: =i 1; p: =p 1; i: =i 1 end; p^. p: =nil;

Существование эйлерова цикла в неориентированном графе для матрицы смежности количество ребер, смежных со всеми вершинами: for i: =1 to n do begin L[i]: =0; for j: =1 to n do if M[i, j]=1 then L[i]: =L[i]+1 end; Проверка существования эйлерова цикла: p: =1; for i: =1 to n do if odd(L[i]) then p: =0; if p=1 then СУЩЕСТВУЕТ else НЕ СУЩЕСТВУЕТ;

Вычисление эйлерова цикла в неориентированном графе для матрицы смежности new(p); pb: =p; p^. s: =1; p^. p: =nil; for i: =1 to n do U[i]: =1; while p<>nil do begin j: =p^. s; k: =U[j]; while (k<=n)and(M[j, k]=0) do k: =k+1; U[j]: =k; if k<=n then begin p 1: =p^. p; i 0: =p^. s; i: =0; p 0: =p; while i<>i 0 do begin new(p 2); p^. p: =p 2; i: =p^. s; k: =U[i]; while (k<=n)and(M[i, k]=0) do k: =k+1; U[i]: =k; M[i, k]: =0; M[k, i]: =0; i: =k; p 2^. s: =k; p: =p 2 end; p^. p: =p 1; p: =p 0 end else p: =p^. p end;

Вычисление всех возможных гамильтоновых циклов в графе для матрицы смежности procedure hamilton(k: integer); var i, j: integer; begin i: =P[k-1]; for j: =1 to n do if (R[j]=0)and(M[i, j]=1) then begin P[k]: =j; R[j]: =1; if k=n then begin if M[j, 1]=1 then ВЫВОД end else hamilton(k+1); R[j]: =0 end; Вызов: for j: =1 to n do R[j]: =0; P[1]: =1; R[1]: =1; hamilton(2);

Вычисление всех возможных гамильтоновых циклов в графе для массива смежных вершин procedure hamilton(k: integer); var i, j, q: integer; begin q: =P[k-1]; for i: =S[q] to S[q]+L[q]-1 do begin j: =D[i]; if R[j]=0 then begin P[k]: =j; R[j]: =1; if k=n then begin {Упорядоченные номера в D} if D[S[j]]=1 then ВЫВОД end else hamilton(k+1); R[j]: =0 end;

Вычисление топологической сортировки Количество ребер, входящих во все вершины: for i: =1 to n do R[i]: =0; for i: =1 to n do for k: =S[i] to S[i]+L[i]-1 do begin j: =D[k]; R[j]: =R[j]+1 end Массив P – очередь вершин, в которые нет входящих дуг: k: =0; t: =1; for i: =1 to n do if R[i]=0 then begin k: =k+1; P[k]: =i end;

Вычисление топологической сортировки while t<=k do begin i: =P[t]; for j: =S[i] to S[i]+L[i]-1 do begin q: =D[j]; R[q]: = R[q]-1; if R[q]=0 then begin k: =k+1; P[k]: =q end; t: =t+1 end;

Вычисление обратной перестановки: for i: =1 to n do Q[P[i]]: =i;